Search for:
Category

Mathématiques

Category
Mathématiques

Le classement ELO

Aujourd’hui j’évoque le (mal-nommé) « classement » ELO, et son utilisation aux échecs et dans d’autres disciplines. https://youtu.be/9oRDksmH0zM Celles et ceux qui connaissent le domaine de l’apprentissage automatique auront peut-être reconnu une certaine similarité. Ce qu’il y a derrière le système ELO, c’est un modèle avec des paramètres qu’il faut « appendre » (le niveau intrinsèque de chaque joueur), et on ajuste les valeurs à chaque itération proportionnellement à un écart entre une valeur prédite par le modèle…

Read More
Informatique

L’algorithme de Diffie-Hellman

La vidéo du jour traite d’un algorithme de cryptographie qui m’a semblé au premier abord invraisemblable…Cela fait plusieurs fois que je traite de cryptographie, et je n’ai pas encore épuisé le sujet, loin de là ! https://www.youtube.com/watch?v=1Yv8m398Fv0 Quelques précisions d’usage sur des points que je traite dans la vidéo. J’ai parlé du chiffre de Vigenere (sans le nommer d’ailleurs, pour pas complexifier) sans forcément élaborer sur le fait que ça n’est pas la seule méthode…

Read More
Mathématiques

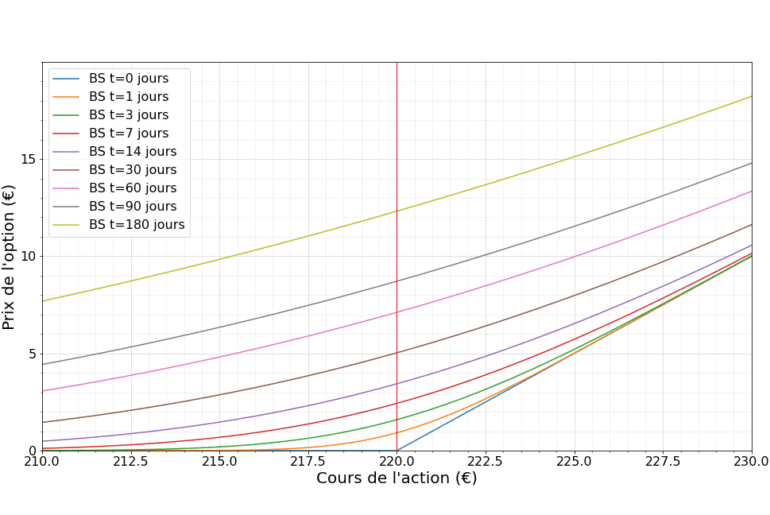
La formule de Black-Scholes

La vidéo du jour parle d’un concept central des mathématiques financières : le pricing des options à l’aide de la formule de Black-Scholes. https://youtu.be/XE7FKLfZzBA Intérêts et dividendes Si vous connaissez un peu le sujet, vous aurez remarqué que pour des raisons de simplicité, j’ai ignoré l’effet des taux d’intérêt. Mais dans le cas le plus général, on considère qu’il existe un placement sans risque fournissant un intérêt $latex r$, et on peut aussi ajouter optionellement…

Read More
Informatique

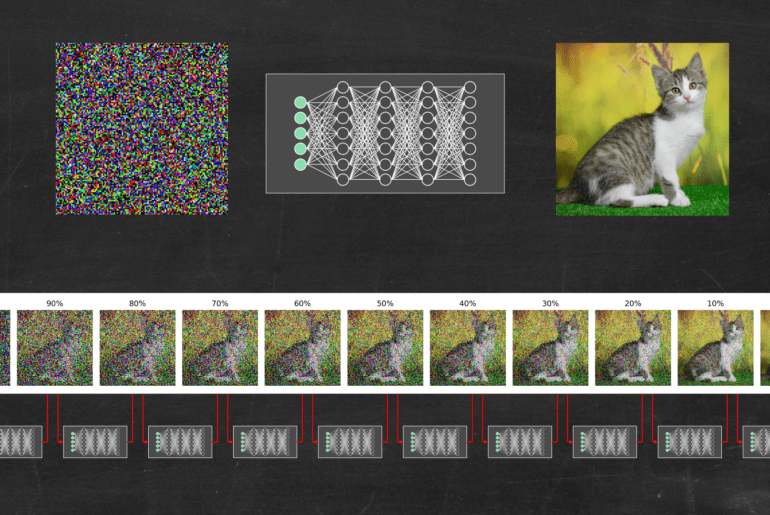
IA génératives et méthodes de diffusion

La vidéo du jour explique quelques principes derrière les algorithmes d’IA générative qui fonctionnent selon les méthodes de diffusion. https://youtu.be/tdelUss-5hY Pour commencer, quelques références importantes sur le sujet. Tout d’abord l’article qui pour la première fois a proposé les méthodes de diffusion Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., & Ganguli, S. (2015, June). Deep unsupervised learning using nonequilibrium thermodynamics. In International Conference on Machine Learning (pp. 2256-2265). PMLR. Le papier qui a démocratisé leur usage…

Read More
Informatique

Comment craquer le jeu WORDLE / SUTOM

Dans ma dernière vidéo, je me suis amusé à écrire un bout de code qui propose une résolution automatisée des jeux à la WORDLE ou SUTOM. Tout ça m’a évidemment été inspiré par la formidable vidéo de 3Blue1Brown sur le sujet ! https://youtu.be/iw4_7ioHWF4 J’avais promis dans la vidéo que je partegerai le code, alors le voici avec quelques explications. Le code est disponible ici : https://github.com/scienceetonnante/WordleSutom Il n’y a vraiment rien de sophistiqué dans l’algorithme…

Read More
Mathématiques

L’effet Casimir et la série divergente 1+2+3+4+…

J’avais déjà traité le sujet en blog, et je m’étais donc promis de ne jamais parler de 1+2+3+4 + … = -1/12 en vidéo…eh bien j’ai craqué ! Dans ce nouvel épisode je vous explique en quoi l’effet Casimir n’est pas une « preuve » de ce résultat, mais il illustre l’utilité en physique de certains concepts des séries divergentes. https://youtu.be/jyQ_hUVI4Gk Dans la vidéo, j’ai traité le cas « académique » de l’effet Casimir, c’est-à-dire en 1D et sur…

Read More
Informatique

Comment les IA comprennent-elles notre langue ? Le traitement du langage naturel

Dans la vidéo d’aujourd’hui, on parle des méthodes de traitement du langage naturel, et comment les techniques de deep learning dominent aujourd’hui les algorithmes de traduction ou de complétion de texte. https://youtu.be/CsQNF9s78Nc L’idée de cette vidéo est née après celle sur Alpha Fold. J’y évoquai en passant les transformers, et je me suis dit qu’il fallait faire une vidéo sur ces fameux transformers ! Et puis en faisant la biblio et en écrivant la vidéo,…

Read More
Géologie

Krachs boursiers, tremblements de terre et criticalité auto-organisée

La vidéo du jour est peut-être un peu velue, mais c’est le genre de sujet que j’aime ! https://youtu.be/MrsjMiL9W9o Quelques compléments d’usage : Largeur à mi-hauteur et écart-type Un point intéressant sur la manière dont j’ai fitté une gaussienne sur les fluctuations du CAC40. J’ai utilisé la largeur à mi-hauteur plutôt que de simplement calculer l’écart-type. Dans une gaussienne, les deux sont reliés car la largeur à mi-hauteur vaut $latex 2\sqrt{2\log 2}\sigma \approx 2.355\sigma.&s=2$ Le…

Read More
Mathématiques

Écrire les nombres : développement décimal et fractions continues

C’est bientôt la rentrée, alors on commence à se réchauffer les neurones avec un peu de maths ! La vidéo du jour est un patchwork de petites choses dont j’avais envie de parler https://youtu.be/CwqoAVMzgp4 Au sujet du développement décimal de la diabolique égalité 0.9999… = 1, la démonstration qui me satisfait le plus est certainement celle qui se base sur une définition du développement décimal sous forme de série dans une base b. $latex x…

Read More
Informatique

Markov Chain Monte Carlo, ou comment déchiffrer n’importe quel code secret

La vidéo du jour traite d’un sujet que j’avais évoqué dans mes articles précédents sur les codes secrets, et sur la machine à inventer des mots : la méthode « MCMC » qui permet de déchiffrer avec une excellente efficacité à peu près n’importe quel message chiffré par substitution. https://www.youtube.com/watch?v=z4tkHuWZbRA Pour cette vidéo, je me suis surtout basé sur l’article introductif de Perci Diaconis Diaconis, P. (2009). The markov chain monte carlo revolution. Bulletin of the American…

Read More