La vidéo du jour est peut-être un peu velue, mais c’est le genre de sujet que j’aime !
Quelques compléments d’usage :
Largeur à mi-hauteur et écart-type
Un point intéressant sur la manière dont j’ai fitté une gaussienne sur les fluctuations du CAC40. J’ai utilisé la largeur à mi-hauteur plutôt que de simplement calculer l’écart-type.
Dans une gaussienne, les deux sont reliés car la largeur à mi-hauteur vaut
\(2\sqrt{2\log 2}\sigma \approx 2.355\sigma.\)
Le fait d’utiliser la largeur à mi-hauteur de mon histogramme plutôt que son écart-type permet de s’affranchir de l’effet des queues épaisses. Une gaussienne de même écart-type aurait été trop large et pas assez piquée au centre.
Le théorème central limite
Je vous fais grâce des controverses sur la bonne manière de nommer ce théorème. Un point intéressant concernant mon illustration avec la taille, et le nombre de déviations standards. La formule qui donne la probabilité d’être à au-moins \(x\sigma\) de la moyenne est
\(1 – \mathrm{erf}(x/\sqrt{2})\)
Voir par exemple https://en.wikipedia.org/wiki/68–95–99.7_rule et le tableau suivant
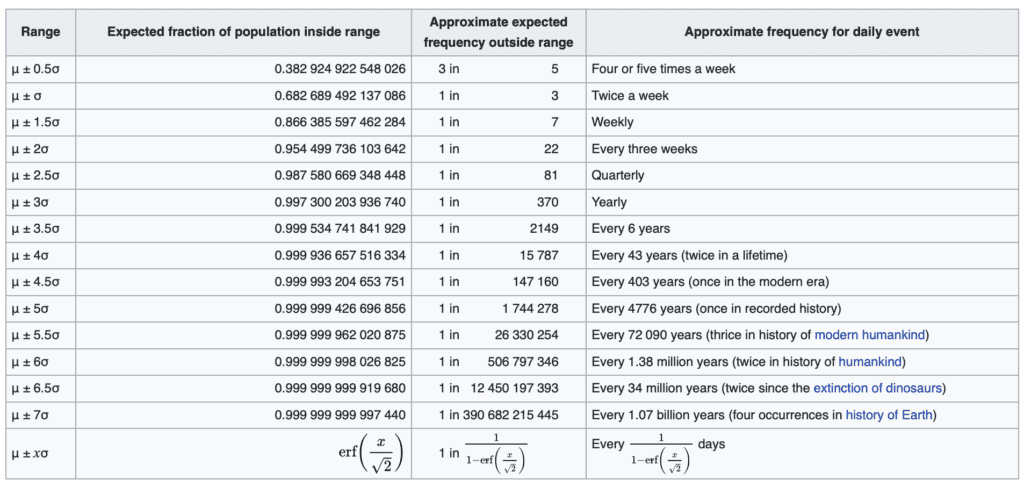
Or il existe plusieurs personnes qui ont été mesurées avec des tailles inférieures à 70cm voire 60cm. On pourrait arguer qu’il s’agit là d’une déviation de plus de 12 déviations standards, qui selon la loi gaussienne ne devrait se produire qu’une fois sur \(2.8\times 10^{32}\). D’ailleurs le raisonnement fonctionne dans l’autre sens, puisqu’il existe des personnes de plus de 2m50. Dans les deux cas, il s’agit de conditions pathologiques due à un phénomène précis (comme une défaillance de l’hypophyse qui sécrete notamment l’hormone de croissance). On peut donc considérer qu’on n’est plus là dans le cas d’application du théorème central limite (accumulation d’un grand nombre de facteurs indépendants), mais dans une situation où un facteur pathologique emporte tous les autres.
Cumul vs distribution
Un petit tour de passe-passe que j’ai fait sans le mentionner dans la vidéo, c’est d’utiliser alternativement la distribution en densité, ou bien en cumulé. Ca ne change évidemment pas grand chose, par exemple pour les fluctuations boursières, c’est la distribution cumulée qui est en \(x^{-3}\), mais la distribution en densité est donc en \(x^{-2}\). Une loi de puissance reste une loi de puissance.
Est-ce abusé de fitter en log/log ?
Une critique qui revient à juste titre concernant les discussions sur les lois de puissance, c’est de savoir si elles en sont vraiment. Notamment, il est assez facile d’avoir des apparentes droites dès lors que l’on fitte en log/log. Pour savoir si c’est raisonnable, il faut regarder sur combien de décades la loi semble tenir.
Dans le cas des tremblements de terre et de la loi de Gutenberg-Richter, c’est pas mal du tout, puisque la partie linéaire semble bien couvrir au moins 5 décades.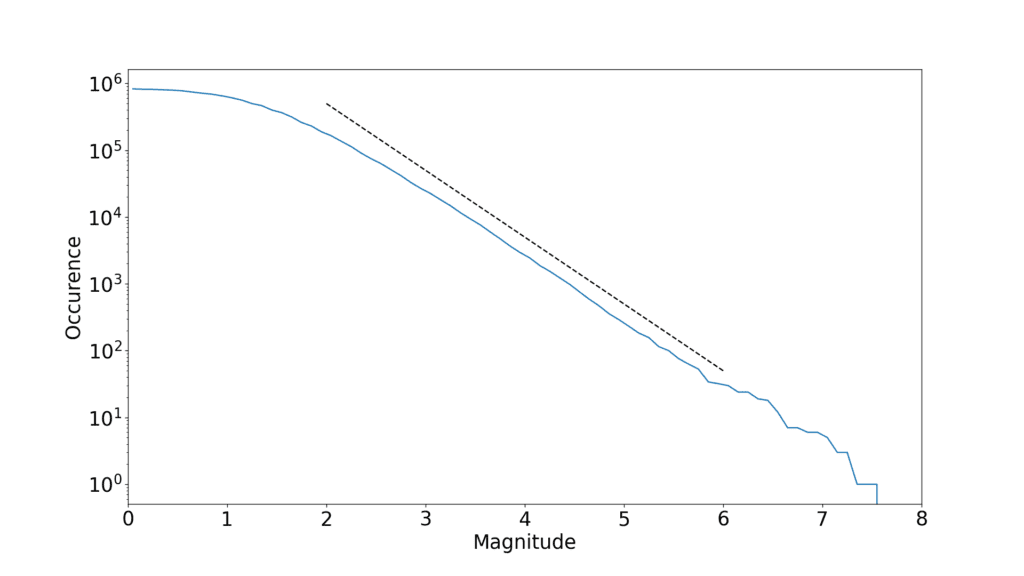 Pour les fluctuations boursières, on peut argumenter que c’est un peu exagéré. Avec les données que j’ai utilisées, on est sur à peine plus de deux décades, ce qui commence à être un peu limite.
Pour les fluctuations boursières, on peut argumenter que c’est un peu exagéré. Avec les données que j’ai utilisées, on est sur à peine plus de deux décades, ce qui commence à être un peu limite. 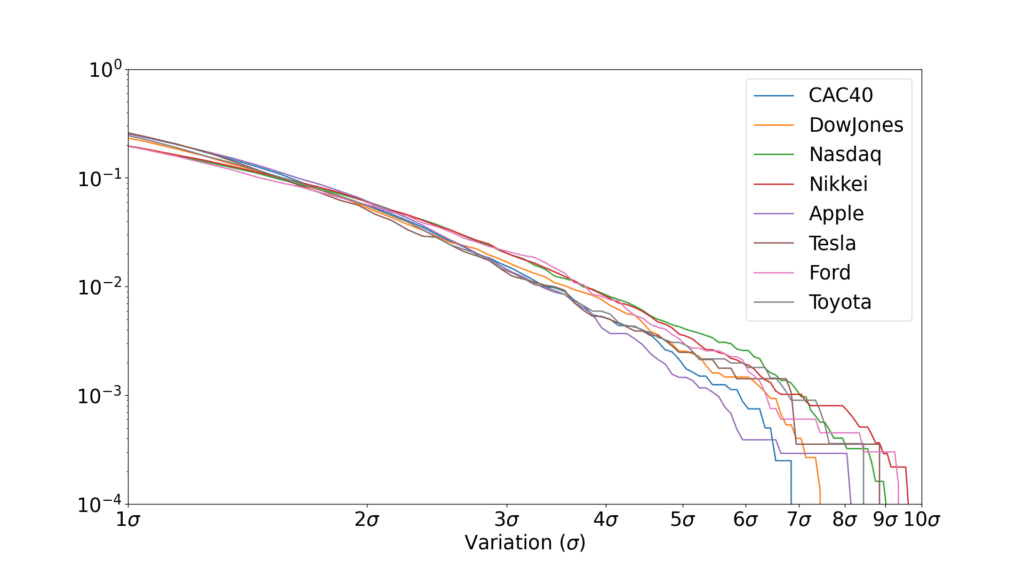
L’échelle de Richter
Aussi étonnant que cela paraisse, j’ai eu un peu de mal à relier de façon fiable l’échelle de Richter aux énergies libérées. L’échelle ayant initialement été dévelopée de façon semi-empirique, il existe plusieurs formulations. J’ai choisi de me reposer sur ce papier
Bormann, P., & Di Giacomo, D. (2011). The moment magnitude Mw and the energy magnitude Me: common roots and differences. Journal of Seismology, 15(2), 411-427.
qui dit « This is the commonly referred to and most widely used “Gutenberg-Richter” energy- magnitude relationship ».
A noter d’ailleurs dans la formule de distribution de la loi de Gutenberg-Richter, les coefficients et notamment la pente vont légèrement dépendre de la région. Il n’y a donc pas d’universalité « pure » entre les séismes des différentes régions sismiques.
Le modèle du tas de sable
Techniquement, le modèle du tas de sable peut être vu comme un automate cellulaire. Et on peut se demander dans quelle mesure les observations de criticalité auto-organisée vont dépendre du choix du seuil S d’avalanche, du nombre de grains G que l’on redistribue, etc. Il me semble que redistribuer tous les grains ou seulement un certain nombre revient au-même (la différence étant qu’un tapis de grains d’épaisseur S-G va se former en dessous de la partie « dynamique » du tas de sable.) Donc on pourrait imaginer par exemple que l’avalanche ne se déclenche que quand il y a 8 grains, et on distribuerai alors 2 grains dans chaque voisin. Mais dans ce cas il me semble que ça revient au même en prenant des grains doublés. Bref, j’ai ce sentiment que le choix de 4 grains se fait sans perte de généralité. Mais je n’ai pas testé !
Tas de sable et séisme
Concernant la représentativité de l’automate cellulaire du tas de sable, il est à noter que Bak et Tang ont proposé une réalisation expérimentale censée mimer une situation de tremblement de terre. Pour cela ils ont utilisé des blocs reliés entre eux par des ressorts, et qui reposaient sur un sol de sorte qu’il existait un coefficient de frottement statique. Si on déplace choisi aléatoirement un bloc dans une direction, les contraintes s’accumulent (tension des ressorts) mais son contrebalancées par la friction statique du sol. Quand la contrainte passe un certain seuil, on a un glissement du bloc (comme dans une instabilité de type stick/slip) qui relâche ses contraintes mais en les répercutant sur ses voisins.
Voir par exemple
Bak, P., & Chen, K. (1991). Self-organized criticality. Scientific American, 264(1), 46-53.
Bak, P., & Tang, C. (1989). Earthquakes as a self‐organized critical phenomenon. Journal of Geophysical Research: Solid Earth, 94(B11), 15635-15637.






25 Comments
Bonjour!
Merci pour ta vidéo très intéressante! J’aurais une question un peu naïve à propos des gaussiennes et des lois de puissances pour laquelle je n’arrive pas à trouver de réponse satisfaisante en ligne et je me dis que tu pourrais peut-être me donner des pistes.
Je me permet de donner des détails sur l’origine de mon questionnement, car il me semble que les concepts/méthodes que je vais énoncer peuvent t’être familières (au moins de loin). Je ne suis ni mathématicien, ni statisticien de formation, mais juste un thésard en biologie qui doit analyser ses données tant bien que mal 🙂 (j’ai tout appris presque seul et sur le tas, donc pardonne-moi d’éventuelles erreurs conceptuelles).
Je « fit » régulièrement des modèles statistiques bayésiens (avec STAN, une implémentation de MCMC disponible sur python et R notamment) pour analyser mes données. Lors de la définition de mon modèle statistique (variable réponse, variables dépendantes, interactions etc), je dois aussi dire à STAN quelle est le type de distribution de mes données à analyser. STAN va ensuite estimer par MCMC les distribution postérieures des paramètres définis pour prédire un « faux » jeu de données et c’est l’une des méthodes de vérification du fit: je compare toutes mes distributions de données prédites avec ma vraie distribution de données et si ça semble coller, c’est un indicateur de bonnes prédictions, donc de bon fit.
Bref j’en viens à ma question sur les gaussiennes et les lois de puissance:
J’utilise souvent une distribution T (Student’s T) pour décrire mes données, car je calcule des ratios et la cloche de mes données brutes a donc souvent une queue épaisse. Il me semble que la loi de Student est tout de même une gaussienne, non? Quand tu parles de gaussienne dans ta vidéo, tu ne mentionnes pas la loi Normale, donc je suppose que tu parles de plusieurs types de distributions gaussiennes.
Je n’arrive pas bien à comprendre la différence conceptuelle (ou le lien) entre la loi de Student et les lois de puissance, car si je devais modéliser les données de bourses de ton exemple, mon premier réflexe en voyant que les queues sont plus épaisses, aurait été d’utiliser une loi de Student et ça aurait été un fit plus satisfaisant qu’une loi normale.
Je vois bien qu’il n’y a pas de 1/x^a dans la formule d’une loi de Student, mais à part ça, je ne comprends pas ses liens ou sa différence conceptuelle avec les lois de puissance.
J’espère que ma question n’est pas trop confuse, je me rend bien compte que j’ai du mal à cerner mon problème, notamment parce que je ne suis pas matheux et que je n’ai pas d’éducation formelle en stats ou en modélisation, donc je te remercie d’avance si tu prends le temps de me lire! 🙂
Au plaisir de découvrir ta prochaine vidéo,
Antoine
Salut,
Le terme « gaussienne » désigne les FONCTIONS en exp(-x^2). Le terme « loi normale » désigne une LOI DE PROBABILITÉ, dont la la densité de probabilité est une fonction gaussienne (désolé pour les majuscules mais je ne peux pas mettre en italique ou en gras!).
Je ne connaissais pas la loi de Student avant de lire ton post, mais d’après la page Wikipedia, ce n’est pas une loi normale, en revanche elle tend vers une loi normale quand un certain paramètre tend vers l’infini (c’est-à-dire que sa densité de probabilité tend vers une fonction gaussienne).
Je ne comprends pas bien ta question de « différence conceptuelle » donc je vais répondre de manière un peu générale. La différence, c’est tout simplement que la loi de Student a une fonction densité de probabilité qui n’est pas une loi puissance ou une gaussienne, mais une fonction d’une autre forme (un peu plus compliquée mais qu’on arrive à écrire, si j’en crois wikipedia). De manière plus générale, si tu prends n’importe quelle fonction f dont l’intégrale vaut 1, tu peux définir une loi de probabilité dont la densité de probabilité est f. (Il faut que l’intégrale vaille 1 puisque la probabilité totale est 1). A noter que n’importe quelle fonction f dont l’intégrale est finie (disons qu’elle vaut V) fera l’affaire, puisque tu peux définir une nouvelle fonction g= f/V dont l’intégrale vaudra 1.
Pour fitter une fonction avec des données, on peut jouer en testant différents types de fonctions et différents paramètres. Idéalement, on aime bien avoir une justification physique (ex: « de nombreux phénomènes semblent logiques à modéliser par une loi normale à cause du théorème central limite »), un modèle (ex: « j’ai écrit les équations, j’en déduit que mes données doivent suivre une fonction de telle forme mais il me manque juste la valeur des paramètres, donc je vais les trouver de manière empirique en fittant les données ») ou même simplement des références (ex: « dans tels papiers ils utilisent une loi de cette forme pour telle ou telle raison, donc je vais faire pareil »), mais au pire ça peut aussi être complètement empirique (« bon bah j’ai testé plusieurs fonctions et il se trouve que celle-ci colle très bien »).
J’espère que c’est un peu plus clair !
Merci pour ta réponse, EK! J’apprécie.
En fait, après avoir laissé reposer le sujet un moment, je crois qu’au fond ma question se résume à « pourquoi choisirait-on plutôt une loi de puissance, au lieu d’une loi de Student pour modéliser des distributions avec des queues épaisses? »
Est-ce simplement parce qu’il y a des limites à l’épaisseur de queue qu’une student peut décrire et qu’une loi de puissance va plus loin? Comme, d’après ce que j’ai pu voir, utiliser une loi de student en cas de grosses queues est assez standard (ça a même un nom, « robust regression » pour des cas avec des valeurs extrêmes/ »outliers »), je me demandais simplement pourquoi on ne l’utiliserais pas.
Mais, comme tu dis, on se base soit sur une convention déjà établie, soit sur une trouvaille empirique au cas-par-cas du style « bon ben cette fonction-là marche, donc je vais prendre ça », donc je suppose qu’il y a tout simplement des cas où une student ne suffit pas et il faut sortir un marteau plus gros :).
Désolé d’avoir mis autant de temps à répondre, je pensais recevoir une notification!
Bonjour,
Pour ceux que ça intéresse, j’ai fait une petite simulation en javascript du tas de sable ici :
https://www.arcadevillage.com/curiosite/ftds.html
J’ai simulé une petite ouverture et un départ sans sable. On voit bien les avalanche, mais on voit aussi que le tas de sable grossit de manière uniforme.
Est-ce du à la programmation et au pseudo-aléatoire de la fonction de randomisation de javascript ?
Sympathique !
Je pense que la différence avec un « vrai » tas (cônique) c’est que là l’avalanche est déclenchée à partir d’un seuil sur le nombre de grains, alors que dans un vrai tas, c’est plutôt le gradient de ça. Une avalanche se déclenche si un coin contient plus de grain que le voisin au delà d’un certain seuil (ce qui est l’équivalent micro d’un angle critique au delà duquel le tas subit une avalanche)
Hello ! Excellente présentation ! Merci pour tout ton travail de vulgarisation. Je laisse un petit message pour signaler un cours passionnant sur cette question au collège de France : De la physique statistique aux sciences sociales : les défis de la pluridisciplinarité
https://www.college-de-france.fr/site/jean-philippe-bouchaud/course-2020-2021.htm
J’ai surtout suivi le cours inaugural, j’ai malheureusement pas le niveau pour le reste, mais c’était passionnant.
Pingback: Krachs Boursiers & Tremblements De Terre – Alltotic
Bonjour, merci, très instructif.
A quand la prochaine variation négative de x% (-30%) du dow jones par exemple?
A quand un seisme de 8 en Californie?
D’après les courbes présentées est-ce que les statistiques permettent de faire des prédictions, si oui quelle est la barre d’erreur?
Roland
Bonjour David, j’ai signalé sur Youtube que la distribution du nombre d’habitants des villes dans la simulation était log-normale et non zipf mais Youtube censure le graphe systématiquement. Je le partage donc ici: https://justpaste.it/74gg1
Bonne continuation!
Salut dobotube et peut être David. Je ne sais pas si c’est très intéressant mais je fais part d’une petite anecdote en lien avec ce commentaire.
Il est, je trouve, très difficile de différencier les queues de distributions log normal et loi de puissance, du moins de mon expérience et en utilisant des Maximum Likelihood estimator. C’est assez surprenant puisque la théorie des valeurs extrêmes les fait tomber dans des classes d’universalités très différentes : queues exponentielles pour le log normal et puissance pour les lois de puissances. Tout ça pour dire que les deux se ressemblent souvent beaucoup au moins du point de vue pratique pour l’estimation des paramètres de ces queues de distribution. Et d’ailleurs je me demande si choisir l’une ou l’autre ne revient juste pas à choisir un set d’hypothèse…. Je m’explique :
Je me fais un peu de pub mais bon, il y a quelques années j’ai fit en toute honnêteté des modèles en loi de puissance (théorie des valeurs extrêmes lié a la statistique issue de mécanisme de sélection naturelle : https://www.pnas.org/content/113/13/3482 ) pour me rendre compte plus tard que ça pouvait aussi être des queues log normal (additivité des énergies de liaisons entre cible et anticorps et donc physique : https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1008751). Les hypothèses sous-jacentes étant vraiment différentes je n’avais pas checker ces 2 cas de figures sur le moment…
Bref, merci David pour le contenu toujours aussi cool.
Bonjour,
Merci pour la vidéo : top comme toujours
Par curiosité : quel est ton outillage pour réaliser tes simulations (langage, framework, logiciels) ?
—
David
Bonjour David,
je serais très surpris d’avoir une réponse, mais merci pour ces vidéos et surtout pour les brainstorms que tu déclenche en moi. Pour ce vidéo, je ne m’intéresse pas à la bourse particulièrement, mais je m’intéresse à tout sujets qui peuvent demander réflexion et donner le goût d’aller plus loin. J’ai une idée très simple, pas révolutionnaire mais j’aimerais savoir si il y a des travaux qui ont été fait dans cette direction:
Imaginons une modification du modèle du tas de sable en automate cellulaire.
La même grille qu’illustrée dans ta vidéo et le même nombre de point maximal par case, soit 4. Mais, ajoutons un code couleur aux points et une force attitrée à chaque couleur.
Bleu: 50 force
Rouge: 75 force
Vert: 25 force
Jaune: 25 force
*Attention de ne pas confondre “force” et “puissance”
Donc, un code couleur à été assigné à chaque point dans la grille. Est-ce que la disposition des couleurs et la grosseur de chaque groupe irait avec une logique? P-e que oui, p-e que non…
En comptant la “force” de chaque point d’une même couleur participant à la puissance d’une avalanche (exemple une avalanche de puissance 100 ayant 20 points bleus, 40 rouges, 10 verts et 30 jaunes) nous pouvons redistribué cette puissance ailleurs dans la grille même si les points ne se touchent pas.
La force d’une couleur additionné à sa puissance peut déterminer si un point de même couleur étant plus loin dans la grille aura un déplacement même si sa case n’occupe pas 4 points.
Le rayon de la distance entre l’avalanche et ses points de même couleurs dans la grille peut aussi peut interagir avec la possibilité qu’il y aura ou pas un déplacement. Les points ayant une faible distance à l’avalanche auront un plus grand pourcentage que les points étant loin.
Exemple rouge:
40 (responsabilité de l’avalanche)
x
75 (la force de la couleur rouge)
+
25 (puissance générale d’une l’avalanche de puissance 100 incluant toutes les couleurs)
–
Affaibli à 15 de distance en l’avalanche et ce point rouge.
= La probabilité de bouger ce point même s’il ne le devait pas ou de ne pas le bouger même s’il le devait.
*Le nombre de couleur peut varier, peut-être le nombre de domaines dans la bourse et chacun avoir une force qui indique l’importance (Force) qu’ils ont dans l’économie mondiale. Le nombre de couleur pourrait aussi être équivalent aux nombres de participant à la bourse, par-contre nous devrions ajouter un système de parenté pouvant grouper des domaines, donnant la possibilité d’avoir plusieurs parentés possibles pour un participant et ce participant pourrait interagir exceptionnellement avec un autre participant ou parenté qui n’occupe pas. **J’aime aussi imaginer un layer derrière ayant des formes pouvant se déplacer, s’agrandir, se rétrécir, interagir etc… qui attirent ou éloignent tout les points ou seulement une couleur ou bien seulement d’une parenté lorsqu’un point doit choisir dans quelle direction il doit se déplacer. Ce qui peut attirer le KO ou éteindre le feu (black out)
Donc les pourcentages de la responsabilité, de la force, de la puissance générale et de la distance sont à titre indicatif. Le nombre de couleur et si système de parenté il y a restent à déterminer, mais je serait curieux de savoir si en explorant différente matrice interactive ayant plusieurs contraintes entre les parties, nous pourrions arriver à une courbe semblable à celle parlé dans ta vidéo.
Merci beaucoup David pour cette chaine.
Bonjour David,
Merci pour toutes ces vidéos et ces illustrations. Je souhaite améliorer mon python et la manière dont vous l’utilisez correspond exactement à mes lacunes (illustrations, mise à jour de graph et traitement de données ‘proprement’)
Est-il possible d’avoir accès aux scripts et au jupiter notebooks afin d’apprendre en les reproduisant ?
Merci
Yann
PS : Désolé pour le doublon avec le commentaire sur YouTube, j’avais peur que mon commentaire passe trop inaperçu
Bonjour David,
Je cherche à reproduire la simulation de la croissance de la population des villes. Peux tu me dire quelle moyenne tu as pris pour la gaussienne du taux d’accroissement ? Je ne parviens pas à multiplier par 6 la population total au bout de 200 ans …
Merci 🙂
salut, possibilité de donner quelques pistes ou de vulgariser le comment le fameux xavier relie le -1.5 et -3 aux volumes échangés et les fluctuations =) ? sinon pas grave super vidéo merci !
Sur le graph de la minute 9:03, il est estimé que les fluctuations du CAC40 hors de la zone linéaire sont jugées trop rares pour être prises en compte. La fréquence est pourtant autour de 1/1000 pour les écarts 6 %, 7 % et 8 %, ce qui reste une fréquence supérieure à celle des personnes de 2m05 jugée « pas absurde » à 1/8000 plus tôt dans la vidéo.
Exclure ces valeurs ne revient-il pas, en pire, à obérer l’existence d’individus de cette taille ? S’agissant justement des valeurs extrêmes, n’a-t-on pas précisément exclu les krachs (et les bulles) du modèle ?
En fait ça n’est pas tellement que je les exclue (même si c’est ce que je dis :-)) c’est plutôt que commes ces événements sont peu nombreux dans l’échantillon (8000 points donc les événements de fréquence 1/1000 ne seront que quelques uns), on ne peut pas s’attendre à avoir une belle droite, ce qui explique que la forme soit beaucoup plus « en marches d’escalier ». Mais avec une série temporelle plus longue on s’attendrait à ce que ça fonctionne quand même.
Merci, je me rends compte que les données ne sont effectivement pas exclues, mais que le modèle en loi de puissance prévoit tout simplement des fréquences supérieures pour ces événements de forte variation. C’est-à-dire, modulo votre réserve sur la longueur des séries, plus de krachs…à supposer que krach soit bien défini là dessus. Peut-être que cela indique l’existence d’un paramètre de régulation dominant qui ne soit pas indépendant du résultant des autres paramètres. Comme par exemple des règles de suspension de séance, ou des réactions humaines ou logicielles qui endigueraient des boucles de rétroaction trop positives… ou pas.
Bonjour. J’attire votre attention sur une publication de Jean Lahérrere qui a corrélé certaines des distributions que vous présentez avec ce qu’il appelle des « fractales paraboliques ».
Voici ce qu’il en dit récemment
« “Distributions de type fractal parabolique dans la Nature”- Comptes Rendus de l’Académie des Sciences- T.322 -Série IIa n°7-4 Avril 1996 p535-541 http://www.oilcrisis.com/laherrere/fractal.htm, je montrais que les galaxies, les agglomérations urbaines, les tremblements de terre et les réserves pétrolières suivent une distribution fractale parabolique (et non pas linéaires comme la loi de Gutenberg-Richer) » »
Merci pour votre travail.
Pingback: Corrélation Causalité | Pearltrees
Bonjour,
Merci pour cette vidéo passionnante. J’ai notamment découvert les lois de puissance.
Beaucoup d’investisseurs, dont des prix Nobel, ont sous-estimé la fréquence des évènements extrêmes dans leurs modèles mathématiques, et certains ont même finis ruinés. Il y a le fonds LTCM, par exemple.
Je ne sais pas s’ils ont utilisé une loi de puissance, mais certainement les courbes de Gauss et la value at risk, qui ont leur limite.
Bonjour,
Excellente vidéo. J
e me pose la même question David Louapre. Quels outils t-ont permis de réaliser les simulations. Surtout pour le Tas de sable et séisme
Espérant avoir une réponse.
C’est un mélange : du python pour les avalanches et la plupart des analyses statistiques. Pour le modèle de croissance des villes j’ai fait du C++ pour accélérer un peu la simulation
Bonjour,
Est-ce que ce serait possible d’avoir accès au programme pour simuler la croissance des villes ? Je n’arrive pas à comprendre comment on arrive à une distribution en loi de puissance…
Je comprends bien que plus une ville grossit et plus un taux positif va lui rapporter beaucoup d’habitant, mais c’est vrai aussi pour un taux négatif où dans ce cas la ville va en perdre beaucoup…
Du coup, je ne vois pas trop comment marche les poles attracteurs.
Si quelqu’un peut m’éclairer, merci !
Ah oui ça fait partie des codes que j’ai pas encore partagés sur ma page Github, mais je vais essayer de faire ça prochainement !
https://github.com/scienceetonnante