La formule de Black-Scholes

La vidéo du jour parle d’un concept central des mathématiques financières : le pricing des options à l’aide de la formule de Black-Scholes.

Intérêts et dividendes

Si vous connaissez un peu le sujet, vous aurez remarqué que pour des raisons de simplicité, j’ai ignoré l’effet des taux d’intérêt. Mais dans le cas le plus général, on considère qu’il existe un placement sans risque fournissant un intérêt \(r\), et on peut aussi ajouter optionellement le fait que l’actif sous-jacent fournisse un certain dividende \(q\).

On a alors une formule plus générale

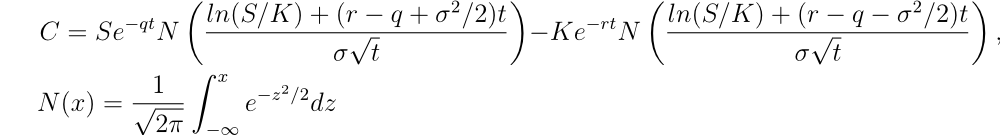
Ca c’est pour une option call. Pour une option put, on obtient une formule légèrement différente mais très similaire dans la forme.

Européennes vs américaines

Un point que je n’ai pas évoqué dans la vidéo : j’ai parlé ici d’options qui ne peuvent s’exercer qu’à un seul moment, c’est-à-dire à la date d’échéance. C’est ce qu’on appelle traditionnellement les options européennes. Mais il existe aussi les options américaines, qui peuvent être exercées n’importe quand jusqu’à la date d’échéance, et pour lesquelles les choses sont un peu plus compliquées.

Mouvement brownien géométrique

A propos du mouvement brownien géométrique, je suis passé rapidement mais c’est un tout petit peu plus subtil que simplement supposer que les pourcentages de variation suivent une gaussienne, car on travaille plutôt sur les rendements. Ce qu’on suppose c’est que si on note \(x_n\) la valeur de l’actif au temps n, la quantité \(x_{n+1}/x_n\) suit une loi log-normale.

Black-Scholes et couverture en delta neutre

Je ne vais pas démontrer ici la formule de Black-Scholes, mais je vais essayer de donner une intuition concernant la couverture en delta neutre. Tout d’abord il faut bien comprendre l’objectif de cette méthode : c’est d’éliminer le risque, c’est-à-dire les aléas. Ca ne veut pas dire qu’on cherche une stratégie qui permette à la banque de gagner de l’argent dans l’opération, mais une stratégie qui permette que ça lui coûte toujours la même chose, quelle que soit la variation du cours du sous-jacent.

Pour cela imaginons la chose suivante : la banque vient de vendre une option, et ne veut pas utiliser la stratégie « attentiste », puisque celle-ci fait courir un risque (elle va coûter plus ou moins cher suivant l’évolution du cours du sous-jacent.) Elle décide donc d’acquérir une certaine quantité \(\Delta\) du sous-jacent (on imagine qu’on peut en acquérir des quantités fractionnaires et sans frais de transaction).

A ce stade, la valeur de sa position est la suivante : elle est short d’une option (puisqu’elle l’a vendue) et long de \(\Delta\) unités du sous-jacent (qu’elle a acheté). Si la valeur de l’option est notée V et celle du sous-jacent S, la valeur du portefeuille est donc

\(P = -V + \Delta S\).

Maintenant imaginons que le cours du sous-jacent évolue, la valeur du portefeuille va également changer. On peut calculer la dérivée de P par rapport à S, et on trouve simplement

\(\frac{\partial P}{\partial S} = – \frac{\partial V}{\partial S} + \Delta\).

Et ce qu’on voit, c’est que cette dérivée peut être nulle si on choisit spécifiquement une valeur de \(\Delta\)

\(\Delta = \frac{\partial V}{\partial S}\).

Le fait que, pour cette valeur, la dérivée soit nulle est intéressant : cela indique que dans cette position, la valeur du portefeuille n’est pas sensible à une petite variation du cours du sous-jacent. C’est exactement ce qu’on cherche : à éliminer le risque.

On peut alors montrer que cela implique que la valeur de l’option suive une certaine équation différentielle. Celle-ci ressemble à l’équation de la chaleur et s’y ramène avec un changement de variable, ce qui permet un calcul explicite de V.

Bien entendu du point de vue de la banque, quand le temps passe et que la valeur du sous-jacent change, alors il faudra recalculer \(\Delta\) et donc ajuster sa position en achetant ou vendant un peu du sous-jacent en continu. Et plus le temps passe, plus la position va évoluer vers une situation où la banque possèdera soit une unité complète du sous-jacent (si le cours à maturité est supérieur au prix d’exercice), soit zéro.

Il est assez utile de visualiser cela en traçant pour un prix d’exercice donné les courbes de valeur de l’option à différentes maturités en fonction du cours du sous-jacent. Voici un exemple pour des maturités allant de 1 à 180 jours sur mon exemple du blé avec un prix d’exercice de 220€.

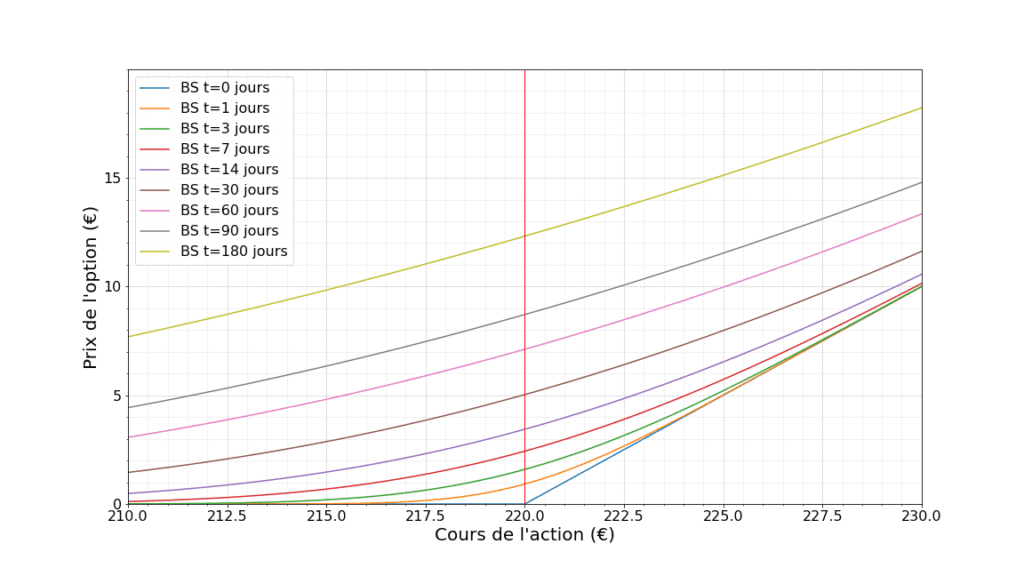
Rappelez vous que la quantité \(\Delta\) que la banque doit posséder à tout instant pour se couvrir est égale à la dérivée de cette courbe. On voit que loin de l’échéance (180 jours), cette quantité est inférieure à 1 et peu dépendante du cours de l’action. Plus l’échéance se rapproche, plus la courbe se rapproche de la courbe bleue tout en bas, et qui est la valeur de l’option à la date de maturité : donc simplement 0 en dessous du prix d’exercice, et l’écart avec le prix d’exercice si on est au-dessus. Or la dérivée de cette courbe est 0 en-dessous du prix d’exercice, et 1 au-dessus.

On voit donc que plus l’échéance se rapproche, plus cette stratégie nous amène à posséder une unité complète du sous-jacent si on est au-dessus du prix d’exercice, et rien si on est en-dessous.

Un point que me mentionnait Gilles d’Heu?reka, c’est qu’une stratégie de trading consiste à moduler la couverture en delta neutre en fonction de ses opinions sur l’évolution du cours du sous-jacent. Si on pense que l’action est sous-évaluée, on va en conserver un peu plus que le Delta, et inversement.