Non, le paradoxe de Simpson ne tire pas son nom de Homer, mais de Edward Simpson, le statisticien qui l’a décrit pour la première fois en 1951. Il s’agit d’un de ces paradoxes mathématiques qui peut nous faire des noeuds à la tête, mais qui malheureusement est bien plus qu’une simple curiosité : bien comprendre ce paradoxe peut s’avérer essentiel pour prendre les bonnes décisions !
Alors si vous ne connaissez pas ce phénomène statistique très contre-intuitif, lisez la suite, et les bras devraient vous en tomber !
Calculs rénaux : quel traitement choisir ?
Pas de chance, on vient de vous découvrir des calculs au rein. Heureusement des traitements existent, et à l’hopital le médecin vous en présente deux. Le premier (appelons le « Traitement A ») consiste en une chirurgie ouverte, alors que le second (« Traitement B ») est une chirurgie qui se fait par de petits trous percés à travers la peau. Le médecin vous demande quel traitement vous préférez. Comme vous souhaitez avant tout guérir, vous demandez au praticien les statistiques de succès de ces deux traitements.
« Oh c’est très simple, vous répond le médecin, les deux traitements ont été testés chacun 350 patients, et voici les chiffres : le traitement A a fonctionné dans 273 cas et le traitement B dans 289 ».
L’affaire semble entendue, le traitement B a marché avec 83% de réussite, contre 79% seulement pour le traitement A. Vous choisissez donc le traitement B.
Mais en repartant de l’hôpital, vous croisez un autre médecin à qui vous demandez son avis sur les traitements. « Oh c’est très simple, vous répond-il : les deux traitements ont été testés 350 fois chacun sur des patients, ces derniers pouvant être atteints soit de ‘petits’ calculs, soit de ‘gros’ calculs, et voici les chiffres » :
Comme vous pouvez le constatez, si vous avez des gros calculs, le traitement A fonctionne mieux, et si vous avez des petits calculs, le traitement A est aussi le plus efficace. Voilà qui est en totale contradiction avec ce que vous a dit le premier médecin. Et pourtant, vous avez beau compter et recompter, sur la ligne « Total », il s’agit bien des mêmes chiffres que ceux présentés par le premier médecin…
Comment est-il possible que le traitement B soit meilleur au global, mais qu’il soit inférieur au traitement A aussi bien sur les petits que sur les gros calculs ? Et ça n’est pas une blague, ces chiffres sont issus d’une vraie étude [1] ! Il n’y a aucune entourloupe statistique ou aucune manipulation, ce que vous lisez là, c’est bien la réalité des chiffres. Vous avez là un bel exemple du paradoxe de Simpson.
Fumer, c’est bon pour la santé
Pour vous aider à appréhender le paradoxe, je vais vous en présenter un autre exemple, lui aussi issu d’une étude réelle [2], et qui devrait vous paraître un peu plus clair. Dans cette étude, 1314 femmes ont été suivies pendant 20 ans, et l’objectif était de comparer le taux de mortalité des fumeuses et des non-fumeuses.
Après 20 ans, le taux de mortalité chez les fumeuses était de 24%, alors que celui des non-fumeuses était 31%. Alors, est-ce que non-fumer tue ?
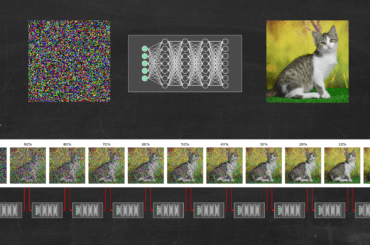
Examinons les chiffres de plus près. Dans l’étude, il y avait 582 fumeuses et 139 sont mortes (cela fait bien 24%), ainsi que 732 non-fumeuses dont 230 sont mortes (31%, pas de problème). Là où le paysage change, c’est quand on représente ces chiffres en séparant par classe d’âge. C’est ce que montre le graphique ci-dessous (que j’ai réalisé en R avec les données smoking du package SMPractical)
Comme vous le voyez, si on raisonne par classe d’âge, dans chaque tranche la mortalité chez les fumeuses a été supérieure à celle des non-fumeuses. On est rassurés, mais comment les chiffres peuvent-ils s’inverser quand on groupe tout le monde ?
Peut-être avez vous senti ce qui cloche : dans la population initiale, il y avait plus de femmes âgées chez les non-fumeuses que chez les fumeuses. Et même si dans chaque tranche d’âge les non-fumeuses meurent moins, cet effet est compensé par le fait que la tranche d’âge « élevée » est sur-représentée chez les non-fumeuses…qui donc en moyenne meurent plus !
Une analyse du paradoxe
Si vous avez bien suivi le cas des fumeuses, vous devriez maintenant être prêts à percer le mystère du paradoxe de Simpson. Tout d’abord comment s’énonce ce paradoxe : il s’agit du fait qu’une corrélation peut disparaître ou même s’inverser suivant que l’on considère les données dans leur ensemble, ou bien segmentées par groupes.
Pour que le paradoxe se produise, il faut 2 ingrédients :
- Premièrement il faut une variable qui influe sur le résultat final (le « groupe »), et qui n’est pas forcément explicitée au départ. On appelle cela un facteur de confusion. Il s’agit de la taille des calculs dans le premier exemple, car celle-ci influe sur la probabilité de succès du traitement, et de l’âge des personnes dans le second exemple, lequel évidemment joue sur la mortalité.
- Deuxièmement, il faut que l’échantillon qu’on étudie ne soit pas distribué de manière homogène : dans le cas du tabac, il y a plus de vieilles femmes dans l’échantillon des non-fumeuses que chez les fumeuses; dans le cas des reins, le traitement « A » est plus souvent donné sur les gros calculs, et le « B » sur les petits (vous pouvez retourner voir les chiffres).
Quand ces deux conditions sont réunies, le paradoxe de Simpson peut se produire ! C’est-à-dire qu’à cause de la distribution hétérogène de l’échantillon, regrouper les données pointe une tendance qui peut être fausse, et qui disparaît si on analyse les données en séparant selon le facteur de confusion.
Des exemples à la pelle
Il existe de nombreux exemples réels du paradoxe de Simpson, en voici quelques uns parmi les plus connus.
En 1973, une étude statistique a mis en évidence le fait que le taux d’admission à l’Université de Berkley était de 44% chez les garçons, contre 35% chez les filles [3]. Une discrimination inacceptable, dont on dit qu’elle donna lieu à un procès (mais je ne suis pas sûr que ce soit vrai).
Toutefois, le tableau change complètement si on s’amuse à regarder ces données en les distribuant par département d’enseignement : alors dans tous les départements, les filles ont un taux d’admission légèrement supérieur à celui des garçons ! Là aussi le caractère inhomogène de l’échantillon est en cause : les filles ont tendance à postuler dans les départements les plus compétitifs, et leur taux d’admission moyen est donc plus faible.
Un autre exemple célèbre est donné par les statistiques de réussite au baseball. En 1995, le taux de succès du batteur David Justice a été meilleur que celui de son adversaire Derek Jeter (25.3% contre 25.0%). L’année suivante, en 1996, même résultat : Justice surpasse Jeter par 32.1% contre 31.4%. Et pourtant, si on combine l’ensemble des deux années 1995 et 1996, Derek Jeter a été le meilleur avec 31% contre 27% ! Troublant, non ?
Un dernier pour la route, histoire de vous montrer l’importance de bien comprendre ce paradoxe pour être un bon citoyen : en 1964 les États-Unis ont voté une loi historique, le Civil Right Act, qui fut un pas déterminant vers l’abolition de la ségrégation raciale.
Sur l’ensemble du pays, 80% des républicains ont voté en sa faveur, contre seulement 61% des démocrates. Étonnant, non, quand on connait les positions de ces deux partis ?
Et pourtant si on distribue ces résultats entre les états du Nord et du Sud du pays, aussi bien au Nord qu’au Sud les démocrates ont plus voté que les républicains en faveur de la loi !
Comment se prémunir du paradoxe de Simpson
J’imagine que vous voyez aisément le potentiel de manipulation qui se cache derrière ce paradoxe : on peut vous faire croire à quelque chose (le chômage a baissé, tel traitement marche mieux, tel individu est meilleur, etc.) alors qu’en regardant les chiffres dans le détail, les effets peuvent disparaître ou s’inverser ! Alors que faire ?
Tout d’abord, il faut se rappeler : cet effet se produit quand il existe une variable cachée influente, et que l’échantillon sur lequel on se base n’est pas homogène. En sciences, c’est pour cela que l’on préfère en général des expériences « randomisées », qui permettent d’assurer une distribution homogène : par exemple si vous avez des calculs rénaux et que vous participez à une expérience pour comparer les traitements, on vous assigne au hasard le traitement A ou B, sans que la taille des calculs influe sur la décision. On gomme ainsi l’inhomogénéité de distribution, et le paradoxe disparaît : le traitement A sera bien vu comme étant le meilleur.
Quand on vous présente des chiffres, il faut donc avoir l’oeil critique, et être particulièrement méfiants quand ces chiffres sont issues de données analysées a posteriori, plutôt que sur un échantillon expérimental qu’on a soi-même construit a priori (en randomisant). (Réfléchissez au point suivant : conclure que « Le lit est l’endroit le plus dangereux du monde, c’est là que la plupart des gens meurent » c’est se tromper car on utilise des données non-randomisées)
Enfin rappelez-vous, ce paradoxe se produit quand il existe une variable cachée fortement influente. Cela signifie que les chiffres bruts ont peu de sens, et doivent être critiqués par un expert du domaine, susceptible de pointer l’existence d’un tel facteur. A l’heure où fleurit la mode du « fact-checking », on a un peu tendance à nous faire croire que les chiffres seraient la vérité « nue ». Non, la vérité nue n’existe pas, et on aura toujours besoin de gens au courant pour interpréter correctement des chiffres, qu’ils soient scientifiques, économiques ou médicaux.
Pour aller plus loin : les facteurs de confusion dans la démarche scientifique
Je suis vraiment loin d’être un expert en stats, mais je voudrais vous présenter un petit exemple fabriqué pour montrer une autre version de ce paradoxe, et comment un traitement statistique adéquat permet de le lever, même quand on a pas travaillé avec des données randomisées. Et puis je vais illustrer ça en R, histoire de ne pas perdre la main.
Imaginons que vous décidiez d’oeuvrer pour le bien de l’humanité, et que vous vouliez étudier l’effet aphrodisiaque de la bière. Pour faire une bonne expérience randomisée, il faudrait prendre des personnes, leur assigner au hasard un certain niveau de consommation de bière, et mesurer l’impact sur leur libido. Malheureusement, c’est évidemment difficile, alors on choisit de travailler sur des données historiques collectées. Vous réunissez donc un échantillon de personnes, et vous leur soumettez un questionnaire permettant d’évaluer leur consommation mensuelle de bière, ainsi que leur libido (sur une échelle de 1 à 10). Vous collectez les données, tracez les résultats.
> plot(Beer,Libido)
> fit <- lm(Libido~Beer)
> abline(fit$coef)
> summary(fit)
Call:
lm(formula = Libido ~ Beer)
Residuals:
Min 1Q Median 3Q Max
-2.820898 -1.043803 -0.007313 1.018204 4.314868
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.5820 0.4479 5.764 9.53e-08 ***
Beer 0.8879 0.1042 8.519 1.96e-13 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.549 on 98 degrees of freedom
Multiple R-squared: 0.4255, Adjusted R-squared: 0.4196
F-statistic: 72.57 on 1 and 98 DF, p-value: 1.956e-13
> pval <- summary(fit)$coefficients[2,4]
> title(main=paste("p-value =",format(pval,dig=3)))
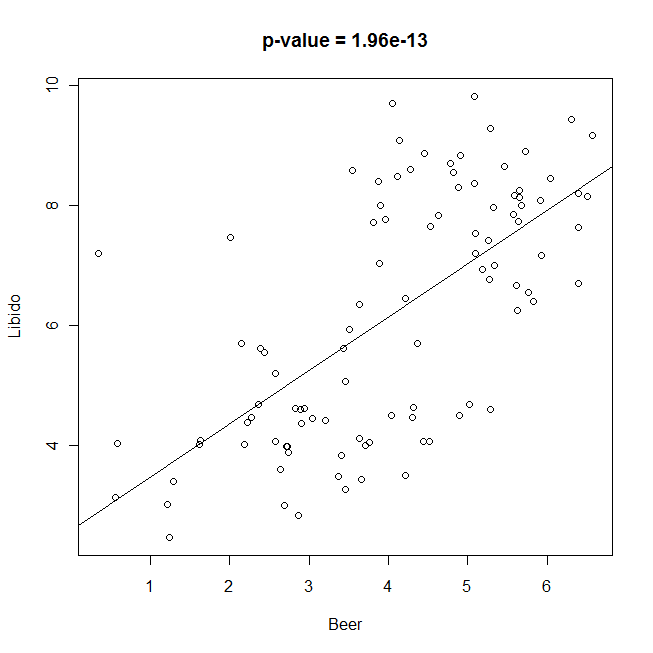
Et là : bingo ! Vous obtenez la courbe ci-dessous, qui montre une belle corrélation positive avec un « petit p » tout à fait significatif pour le modèle linéaire.
La bière influe fortement sur la libido, voici l’aphrodisiaque du futur ! Vous vous préparez donc à soumettre votre manuscrit avec la bénédiction de Kronenbourg.
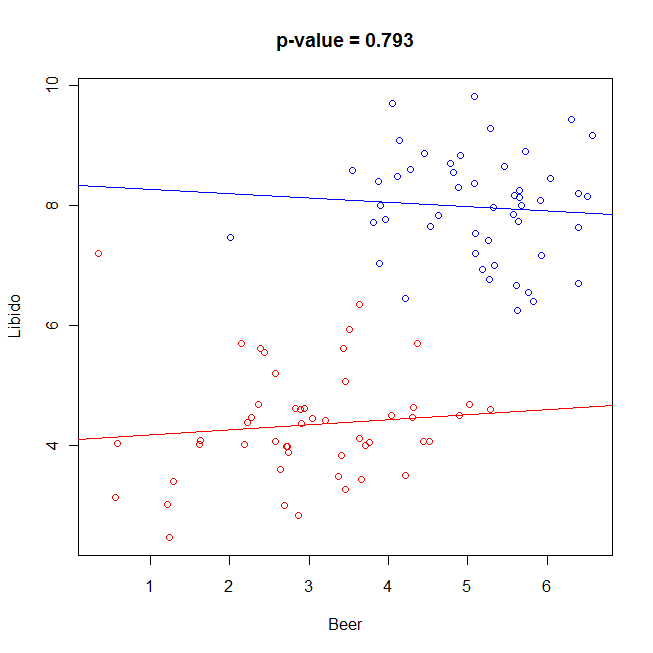
Et là un petit malin vous fait remarquer « Et si tu sépares les hommes et les femmes ? » Vous refaites donc votre graphique en colorant différemment les deux sexes, et là…consternation ! Au sein de chacun des groupes, plus du tout de corrélation ! Et le fit linéaire par groupe est insignifiant.
Un moyen de controler cela, c’est de faire une analyse en controllant d’abord par le sexe. Techniquement, on fait quelque chose comme une ANCOVA, et on prend bien soin de l’ordre des facteurs. En R, tout se fait avec la commande « lm », et on ordonne d’abord le sexe, puis la consommation de bière.
> plot(Beer,Libido,col=c("red","blue")[as.numeric(Group)])
> fit2 <- lm(Libido~Group+Beer)
> summary(fit2)
Call:
lm(formula = Libido ~ Group + Beer)
Residuals:
Min 1Q Median 3Q Max
-1.83333 -0.47439 0.03775 0.47490 2.91397
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.27995 0.29119 14.698 <2e-16 ***
GroupM 3.57795 0.26193 13.660 <2e-16 ***
Beer 0.02321 0.08810 0.263 0.793
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9108 on 97 degrees of freedom
Multiple R-squared: 0.8035, Adjusted R-squared: 0.7994
F-statistic: 198.3 on 2 and 97 DF, p-value: < 2.2e-16
> pval2 <- summary(fit2)$coefficients[3,4]
> title(main=paste("p-value =",format(pval2,dig=3)))
> fitF <- lm(Libido~Beer,data=d[Group=="F",])
> fitM <- lm(Libido~Beer,data=d[Group=="M",])
> abline(fitF$coef,col="red")
> abline(fitM$coef,col="blue")
Et là on voit que le « petit p » pour l’influence de la bière après contrôle par le sexe n’est pas du tout significatif !
Le code qui a fabriqué les données :
> set.seed(42)
> d <- data.frame(Group = c(rep(c("F","M"),each=50)),
Beer = c(rnorm(50,mean=3,sd=1),rnorm(50,mean=5,sd=1)),
Libido = rnorm(100,mean=4.5,sd=1) + rep(c(0,3.5),each=50))
Dernier point pour les plus furieux, qui est en quelque sorte un paradoxe dans le paradoxe : on peut s’imaginer que quand on voit des données agrégées, on peut toujours trouver un facteur à la con (genre signe du zodiaque, nombre de lettres du prénom, etc.) qui va nous donner les corrélations dans le sens qu’on veut une fois que c’est segmenté. Comment être sûr qu’un facteur de ce genre est vraiment « influent » ? Ces questions touchent le coeur du problème de « corrélation n’est pas causation » (dont découle le paradoxe de Simpson). Une solution possible est l’utilisation du formalisme des réseaux bayésiens causaux développé par Judea Pearl. Je n’ai pas eu le courage d’attaquer son livre « Causality« , mais un sympathique compte-rendu se trouve ici.
P
our finir, pour vous rappeler au quotidien de l’existence du paradoxe, vous pouvez vous procurer la tasse à café ci-contre. Je la veux bien pour mon anniversaire …
Billets connexes :
Les probabilités conditionnelles : un autre exemple de statistiques médicales contre-intuitives
Quand l’économie rencontre la génétique : une étude où l’influence d’éventuels facteurs de confusion a été intensément débattue
Chez mes collègues blogueurs :
Ce billet de Tom Roud sur un paradoxe de Simpson évolutif
Ce billet de Dr. Goulu sur l’espérance de vie
Ce billet de Freakonometrics qui illustre le paradoxe avec de la géométrie élémentaire sur les parallèlogrammes.
Références :
[1] Charig, C. R., et al. « Comparison of treatment of renal calculi by open surgery… » British medical journal (Clinical research ed.) 292.6524 (1986): 879.
[2] Appleton, David R., Joyce M. French, and Mark PJ Vanderpump. « Ignoring a covariate: An example of Simpson’s paradox. » The American Statistician 50.4 (1996): 340-341.
[3] Bickel, Peter J., Eugene A. Hammel, and J. William O’Connell. « Sex bias in graduate admissions: Data from Berkeley. » Science 187.4175 (1975): 398-404.
77 Comments
Bonjour,
excellent article, comme toujours. Je pense qu’il y a au cœur de ce paradoxe une hypothèse implicite (mais fausse) : les données statistiques ont été obtenues dans les mêmes conditions que celle dans laquelle on se trouve pour faire un choix.
Je m’explique : si les traitements A ou B avaient été choisis indépendamment de la taille des calculs dans les « expériences » dont les résultats ont produit les données statistiques, alors il serait sensé de considérer que le traitement B est meilleur. Mais en réalité, les traitements ont été réalisés en sachant quelles étaient les tailles des calculs (comme le montrent les sous-populations très inégales), alors que le choix du patient se fait sans cette connaissance. Donc on ne reproduit pas vraiment le protocole initial. C’est en cela qu’on s’écarte de la randomisation.
Ce cas particulier est évidemment plus facile à interpréter que certaines situations réelles, biaisées par des facteurs cachés qui ne sont pas évidents à identifier ; c’est le cas notamment en économie, où les données statistiques disponibles sont historiques plutôt que systématiques.
SG
Oui c’est exactement ce que je voulais illustrer avec mon exemple de la bière. Les données « historiques » ne sont pas randomisées et donc l’analyse agrégée est faussée.
Un point amusant dont je ne sais pas s’il est fréquent : dans plusieurs cas on est « naturellement » à biaiser l’échantillonage dans le sens du paradoxe de Simpson :
– Le traitement A est meilleur, donc on le donne plus dans les cas difficiles (gros calculs), donc il apparait moins bon en moyenne.
– Les filles sont meilleures que les garcons, donc elles postulent plus dans les departements difficiles, donc elles apparaissent moins « admises » sur les données agrégées.
« Les filles sont meilleures que les garcons, donc elles postulent plus dans les departements difficiles »
L’échantillon sous considération sont des filles qui postulent à Berkeley, qui est une université connue pour son gauchisme extrême. Il se peut donc qu’elles s’attendaient à un traitement de faveur en raison de leur sexe et qu’elles postulaient pour des facultées plus difficiles que si elles ne s’attendaient pas à ce biais favorable.
Et le biais semble bien réel, puisque Berkeley accepte effectivement plus de filles que de garçons.
Il est probable que ce soit dû à la politique et non pas à la performance des filles.
C’est encore pire quand on inclut la discrimination « positive » basée sur la « race ». Oui, c’est raciste, pourtant c’est la politique officielle de l’Etat Américain et d’universitées telles que Berkeley qui reconnaissent l’existence de « races » et qui basent leurs décisions d’admission sur ce critère.
Un homme du Sud-Est Asiatique aura beaucoup plus de peine à entrer qu’une femme noire, même s’il a plusieurs centaines de points SAP d’avance sur elle… et tout ça basé sur des analyses statistiques, qui semblaient indiquer un biais raciste AVANT ces lois qui sont explicitement racistes.
On nage en plein délire …
Pingback: Le paradoxe de Simpson : les stats peuvent &eci...
Encore un super billet David 🙂
Je ne connaissais pas le travail de Judea Pearl, mais il y a aussi les « path analysis » qui essayent de démêler corrélation et causalité..
http://4.bp.blogspot.com/-mGkjnYLuOQc/UTEQOGqCfNI/AAAAAAAABFE/8vnKjRH0GkQ/s320/correlation.gif
Pingback: Notes pour plus tard
David, ce n’est vraiment pas gentil non seulement de piquer mon idée d’article qui est sous forme de brouillons depuis 4 mois, mais en plus de le traiter bien mieux et bien plus clairement que ce que je n’aurais jamais pu faire 😉 bravo à toi, c’est vraiment intéressant et troublant ces paradoxes statistiques.
Merci 🙂 Tu peux y aller, le sujet mérite bien plusieurs billets ! Je suis sûr qu’il y a encore beaucoup à faire, notamment sur « corrélation n’est pas (toujours) causation »…
tiens, un ami me fait remarquer que c’est le pourcentage de mortalité à 20 ans sur le graphe des fumeuses et non pas des survivants.
Bien vu ! Je suis bon pour refaire mon graphe. Tiens ca tombe bien, je vais pouvoir aussi corriger « fumeurs »en « fumeuses »!
Done !
Question bête peut-être mais pour bien comprendre : Pourquoi les chiffres diffèrent-ils entre le traitement A et le traitement B ? Par exemple sur les calculs de moins de 2cm on applique le traitement A à 87 patients et le traitement B à 270 patients…..
L’échantillon de patients change t-il entre les deux traitements ? Dans ce cas, il ne s’agirait pas d’un paradoxe.
Bref, une explication serait la bienvenue car je nage un peu là.
Merci d’avance
Oui, c’est exactement ca !
Si le paradoxe est possible, c’est justement parce que les chiffres diffèrent ! Si le traitement A avait autant été donné que le B dans chacun des deux cas, alors on aurait pas vu d’anomalie dans les pourcentages.
C’est pour cela que pour tirer des conclusions fiables, on essaye en général de faire des experiences randomisées. Dans le cas des calculs, ca n’etait justement pas randomisé. Ce qu’il se passe, c’est que pour les médecins, le traitement est réputé plus efficace. Du coup pour les cas difficiles (gros calculs), c’est plutôt celui-ci qui a été donné. Inversement pour les cas faciles, c’est plutôt le B qui a été choisi car je pense qu’il est moins lourd.
Merci pour votre réponse, très claire David. Donc ce cas, au delà de la randomisation que l’on peut effectuer en amont, ne serait-il pas judicieux de pondérer les segments en affectant des coefficients en fonction de l’échantillon.
Par exemple, un test réalisé sur 500 personnes pourrait-être considérer 5 fois plus fiable qu’un test réalisé sur 100 personnes.
Dans notre cas,
pour les petits calculs 370/87=3.1
Pour les gros calculs 263/80=3.28
Ce qui me donnerait
(93+(73*3.28))/4.28 = 77.67 % en moyenne pour le traitement A
(87+(69*3.10))/4.1= 75.22% en moyenne pour le traitement B
Dans ce cas, on peut se rendre compte que le traitement A est bien le plus efficace.
Je précise que je ne suis pas dans le domaine mathématique ou statistique mais juste un amateur curieux et passionné par les maths donc, désolé si mes questions et réflexions semblent in à propos ou maladroites.
Bonne journée
L’idée est intéressante, mais je ne pense pas qu’elle soit correcte. En effet ca n’est pas un problème de fiabilité, dans le sens oú le paradoxe existerait toujours, même avec un échantillon composé de millions de personnes (or si on augmente la taille de l’échantillon, on améliore la fiabilité). Ce qui compte c’est plutôt la représentativité de l’échantillon. Or ici ca n’est pas le cas : le traitement B n’a pas été donné sur un échantillon représentatif des calculs rénaux, car on l’a plus souvent utilisé pour des calculs « petits ». La randomisation permet justement d’avoir à coup sûr un échantillon représentatif.
Une manière peut être plus intuitive d’aborder le pararoxe est de regarder l’exemple que je donne à la fin avec la bière. Il est un peu différent dans le sens que ce qui remplace la variable « traitement A ou B » c’est une variable continue « conso de bière ». Mais je trouve ca un peu plus facile à percevoir graphiquement.
Génial cet article j’ai vraiment appris quelque chose!
Pingback: Le paradoxe de Simpson | C@fé des Scienc...
« Sur l’ensemble du pays, 80% des républicains ont voté en sa faveur, contre seulement 61% des démocrates. Étonnant, non, quand on connait les positions de ces deux partis ? »
J’ai de sérieuses réserves à émettre sur cette dernière remarque : en effet, c’est précisément sous la présidence de Lyndon Johnson dans les années 60 que le parti démocrate américain a changé (d’électorat, notamment). Jusqu’alors, si mes références sont exactes, le Sud escalvagiste puis ségrégationniste votait majoritairement pour le parti démocrate. L’abolitionnisme, notamment, a été porté par le républicain Lincoln. Lorsque les démocrates ont fait passer le Civil Rights Act, les ségrégationnistes (sudistes blancs) ont reporté leurs voix sur les républicains et l’attachement partisan s’est plus ou moins inversé.
Billet tres utile pour ceux qui n’ont pas l’habitude des stats’.
Quelques remarques en vrac :
– la solution la plus naturelle a ce paradoxe qui n’est pas evoquee dans cet article est l’analyse multivariee (regression lineaire multiple) ;
– il y a parfois une legere confusion avec la question du biais de selection qui devrait aussi etre evoquee il me semble ;
– comme vous ecrivez vous meme « correlation n’est pas causation », il serait bon d’eviter d’ecrire « la biere influe sur la libido » qui est deja une affirmation causale ;
– il me semble d’ailleurs qu’on parle davantage de « causalite » que de « causation ».
« la solution la plus naturelle a ce paradoxe qui n’est pas evoquee dans cet article est l’analyse multivariee (regression lineaire multiple) »
Mais si, c’est précisément de ca que je parle ! Mais le nom qu’on donne dépend de la nature des variables considérées.
Une ANOVA ou une ANCOVA sont aussi des analyses mutlivariées. Simplement on donne (de manière une peu facheuse je trouve) des noms savamment differents suivant la nature des variables :
– Dans le cas des calculs rénaux : deux variables discrètes (traitement et taille des calculs), donc on doit faire une ANOVA
– Dans le cas bière/libido : une variable continue (bière) et une variable discrète (sexe), donc on fait une ANCOVA
– Si on avait considéré un facteur confondant continu (le poids par exemple), on aurait fait une régression multilinéaire.
Encore une fois, je n’aime pas trop l’idée d’avoir des noms différents pour ces 3 concepts. C’est pour ca que j’aime bien la facon de formuler en R, où justement toutes ces analyses se font avec la même commande « lm » pour « linear model ». Et suivant la nature des variables, la fonction se débrouille toute seule !
Sinon pardon pour l’anglicisme, effectivement causalité est le mot correct 🙂
Oui effectivement vous avez raison, voici les chiffres qui illustrent le paradoxe :
Democrat Republican
Northern 94% (145/154) 85% (138/162)
Southern 7% (7/94) 0% (0/10)
Both 61% (152/248) 80% (138/172)
On y retrouve bien les ingrédients du paradoxe de Simpson :
* le facteur confondant Nord/Sud est plus influent que le parti
* en controllant pour la region, les democrates un peu plus favorables que les republicains
* MAIS comme vous le dites, le sud vote majoritairement democrate.
Si le sud avait vote republicain, le paradoxe aurait disparu. De meme que le paradoxe des calculs renaux aurait disparu si on avait plus donne le traitement A dans les cas « faciles ».
Dans la mesure ou vous ecrivez un billet de vulgarisation, il me parait simplement bizarre de parler d’ANOVA et d’ANCOVA, concepts qui me paraissent plus compliques qu’une regression lineaire a plusieurs explicatives. Ce n’est pas exactement la meme chose d’une part, et d’autre part dans le cas d’une regression lineaire la nature des variables (continue ou discrete) n’a aucune importance methodologiquement (ca reste une minimisation de la somme des carres des residus) et l’ordre des facteurs n’a non plus aucune importance, ce qui ne parait pas etre le cas dans l’ANCOVA comme vous l’ecrivez.
Il me parait juste plus simple d’illustrer que les correlations sont conditionnelles (toutes choses egales par ailleurs) plutot que de parler d’analyse de variance (anova et ancova).
P.S. : on dit egalement plutot « causality » en anglais !
Oui c’est de la vulgarisation, c’est bien pour cela que je n’ai parlé d’ANCOVA que dans la partie « Pour aller plus loin » que je réserve traditionellement pour des concepts plus avancés. 🙂
Le paradoxe de Simpson s’énonce « classiquement » avec des variables factorielles, lesquelles peuvent avoir plus de 2 niveaux (comme les départements d’enseignement). Pour appliquer une régression linéaire comme vous le suggérez, il faut binariser chaque niveau des facteurs, puis régresser : ca ne constitue pas une méthode que je qualifierai de « simple » (au sens que je me sens de l’expliquer dans le corps du billet).
Sur la différence au sujet de l’ordre des facteurs, c’est un truc que l’on peut choisir de prendre en compte, ou pas. En fait quand on fait une ANOVA, la minimisation de la somme des carrés des résidus est toujours faite indépendamment de ce choix. Ce qui change c’est la manière dont dont rapporte les résultats (dont vont dépendre ensuite les « petits-p »). Si on veut un truc indépendant de l’ordre des facteurs on fait « type III sum of square », alors que tel que je l’ai illustré, cest du « type I », c’est-à-dire qu’on analyse séquentiellement. C’est vrai qu’en régression linéaire on fait souvent par défaut du type III (pas d’importance de l’ordre).
C’est d’ailleurs une source de confusion fréquente car d’un logiciel à l’autre, on a par défaut du type I, II ou III.
J’ai quand même l’impression que c’est plus correct de faire en « type I » en prenant en compte l’ordre des facteurs. Il faudrait que je vérifie, mais si on fait du « type III » sur l’exemple bière/libido, la bière a peut-être un risque de sortir significative.
PS : sinon « Causation » se dit en anglais. 😉
http://en.wikipedia.org/wiki/Correlation_does_not_imply_causation
Mais il peut y avoir une petite nuance qui m’échappe !
Pingback: manipulation | Pearltrees
Pingback: Le paradoxe de Simpson | Techno & Science |...
Pingback: Grorico's corner
Bonjour, j’ai une petite question de neophite,
ne pourrait on pas utiliser un khi-deux pour contrebalancer les différence d’observation?
Un test du khi-2 sert à tester des différences de proportions entre deux groupes.
Il peut servir par exemple à « confirmer » qu’entre les petits et les gros calculs, la proportion de traitement A/traitement B est « significativement différente ». Ou encore pour attester que les filles et les garçons se répartissent différemment sur les différents départements d’enseignement à Berkeley.
Donc en gros un test du khi2 peut être utile si 1) on a déjà identifié un possible facteur confondant 2) on veut savoir si la répartition de ce facteur confondant diffère d’un groupe à l’autre. Ce test peut donc nous confirmer que l’on est dans une situation « risquée » par rapport au paradoxe, c’est à dire avec distribution inhomogène selon le facteur confondant.
Pingback: Blog de Crampi » Trouvailles 05/05/13
salut, je tenais à te feliciter pour la pertinence des articles de ton blog ! j’édite moi aussi un blog depuis peu et j’espère pouvoir faire aussi bien 🙂 A bientôt, ZAK
Donner des exemples réels, c’est bien pour montrer que ça existe mais donner des exemples fabriqués, ça permet de mieux comprendre ce qui se passe.
Cas A-1 100%: 10 cas sur 10
Cas A-2: 67%: 2000000 cas sur 3000000
Cas B-1 33%: 1000000 cas sur 3000000
Cas B-2 0%: 0 cas sur 10
Cas 1 33%: 1000010/3000010
Cas 2 67%: 2000000/3000010
En gros, quand on raisonne de façon globale, les cas A-1 et B-2 n’existent pas. et les cas A-2 et B-1 prédominent complètement.
Bonjour,
je constate qu’initialement le problème de quasi chaque exemple est une erreur de réalisation de l’étude. Dans le cas du traitement du rein, on n’a pas les mêmes conditions pour le traitement A et le traitement B (270 patients testés avec cette méthode pour un petit calcul et en traitement A contre 87 patient pour petit calcul et traitement B, il aurait fallait la même proportion de gens avec petit calcul et gros calcul pour les 2 traitements). Si on fait varier plusieurs variables, on ne peut plus rien en conclure avec des données agrégées.
On a exactement le même soucis avec l’étude sur les fumeuses/non-fumeuse : ils n’ont pas pris le même nombre de personnes par tranche d’âge, donc plusieurs variables, on ne peut rien en conclure en agrégé!
Bonjour,
Pour moi, votre article nous donne deux pistes d’erreurs en statistiques (alors que vous n’en parlez pas vraiment):
-Cas 1: le paradoxe de Simpson: on a tout simplement un paramètre caché qui influence les résultats de notre test. Le problème consiste donc à obtenir des données randomisés pour éviter d’être influencé par ce paramètre (ce qui n’est pas fait dans les exemples). Jusque là, tout va bien, ça semble classique.
-Cas 2: le test de la bière libido. On a un paramètre caché (le sexe) qui influence les 2 variables testées (libido et bière). Même si on « randomize » nos tests, les résultats resteront erronés. Le seul moyen d’avoir des statistiques réelles est de séparer les groupes, et de faire des statistiques sur chacun des groupes (dans ce cas, il faut prendre en compte l’âge, par exemple, qui influence vraisemblablement la libido et la quantité de bière bue, etc…).
Ça pour moi c’est une nouveauté, et c’est bien plus critique que le cas1, où « il suffit » de prendre des gens au hasard.
Ne pourriez vous pas mettre cet exemple dans l’article pour le grand public, et l’expliquer sans parler du paradoxe de Simpson (pour moi c’est une sorte d’extension, ce n’est pas vraiment la même chose)? Car, souvent, on a pas accès aux données, et on part du principe que les stats sont bien faites (cas 1). On ne peut pas remettre en question et être critique du cas 1 la plupart du temps. Par contre, en y réfléchissant bien, on peut trouver des failles comme pour le cas2 dans de nombreuses statistiques!
Je veux dire que si on nous dit « A=80%, B=90% », on ne peut pas être critique de ce résultat, on ne peut pas vraiment faire quoi que ce soit sans les données brutesx (dont on a pas accès)… par contre, quand on nous donne la courbe « bière // libido », là on peut déceler le problème sans avoir accès aux données brutes!
J’ai quelques exemples en tête que l’on rencontre dans la vie de tous les jours, c’est toujours intéressant comme raisonnement!
Je trouve le cas 2 encore plus intéressant que le paradoxe de Simpson!
J’en profite pour vous remercier pour ce blog, que j’ai littéralement dévoré! Vivement les prochains papiers!
Bravo!!
De la science, accessible, et étonnante! Tout ce que j’aime!
Rémi
Pour moi les deux cas sont véritablement les mêmes (à part la nature discrète ou continue des variables). Mais je crois que votre confusion vient du fait que je me suis peut-être mal exprimé sur ce qu’il faudrait faire pour « randomiser » l’exemple libido-bière.
Randomiser ce n’est pas prendre les gens au hasard, c’est leur attribuer au hasard un niveau de la variable dépendante. En l’occurence là, il faudrait par exemple
* prendre des gens au hasard, on aurait donc 50% d’hommes et 50% de femmes
* leur attribuer au hasard un niveau de consommation de bière et leur demander de s’y tenir ! : on aurait donc autant de femmes que d’homme buvant beaucoup de bière.
et là on s’affranchit du risque de paradoxe.
La beauté de la randomisation, c’est que même si il existe une variable cachée qu’on ne soupconne pas, on engendre naturellement une distribution équilibrée qui nous met à l’abri.
La randomisation est censée être la procédure de choix pour les tests médicaux. Dans le cas des calculs, pour randomiser, il aurait fallu attribuer à chaque patient le traitement A ou B en tirant au hasard (et pas en appliquant préférentiellement l’un des traitements aux cas les plus difficiles).
On en vient à cette conclusion que le seul moyen inconstestable de mettre en évidence un lien de cause à effet, c’est une expérience randomisée.
Superbe.
Non, non, vous l’aviez expliqué dans l’article, j’ai juste zappé la « méthode » de randomisation.
En effet, pris comme ça, c’est à peu près le même problème (avec simplement la variable « bière »).
Merci pour votre explication (rapide qui plus est!)!
Encore bravo pour le blog!
Pingback: 78: Comment convaincre par les maths • Neuromonaco
Pingback: Comment être sûr qu’un résultat scientifique est vrai ? | Science étonnante
Pingback: Alexs12 | Pearltrees
Pingback: Le paradoxe de Simpson | Clin d'oeil | Scoop.it
Pingback: Blog/Forum | Pearltrees
Pingback: Le paradoxe de Simpson | Agence Science-Presse ...
Pingback: Les blogueurs de la santé | Pearltrees
Pingback: Recherche Maïeutique | Pearltrees
Pingback: Sirtin » L’anthologie de blogs de science , 2ème édition - ISSN 2270-1192
Pingback: L’anthologie de blogs de science , 2ème édition | Sirtin science
Pingback: Correlation/causation | Pearltrees
Article très intéressant !
Pingback: Une anthologie des blogs de science, et un débat "Blogs de science & journalisme scientifique" | Science étonnante
Derrière le paradoxe de Simpson il existe une condition très importante qui ne provoque pas toujours le paradoxe si elle n’est pas réalisée mais qui enlève toute possibilité d’usage fiable du résultats du test statistique de comparaison de 2 proportion (ou de 2 moyennes).
Appelons p et p’ les probabilités de guérison par les traitements A et B de votre premier exemple. On veut tester si on peut accepter p=p’ ou au contraire p>p’ ou l’inverse. Chacun admettra facilement que le test n’aura de signification QUE si p et p’ existent. Cela pourrait aller sans le dire mais va mieux en le disant car, la plupart du temps on oublie ce petit détail. SAUF lorsque une autre condition fait apparaître le fameux paradoxe comme dans vos exemples.
En fait, quand on constate sur les données globales que le traitement B est plus efficace que le A on devrait assortir ce constat de la réserve suivante :
« sous réserve que les probabilités p et p’ existent, c’est à dire que chaque malade ait la même probabilité de guérison par A et la même par B. »
Tant qu’on ne le sait pas on ne peut en réalité rien conclure. Mais on passe très souvent outre cette restriction tant chacun à hâte de publier un résultat …
Exemple : les études cas-témoins Tardieu sur le risque de sclérose en plaques après vaccination hépatite B chez les enfants. Le test consiste à comparer les probabilités p et p’ d’avoir été vacciné chez les cas et les témoins. Là aussi il est essentiel de s’assurer que p et p’ existent avant de prétendre les avoir valablement comparées.
Or les enfants jeunes (<10 ans) ont été vaccinés à 25% environ alors que les classes d'âges vaccinées en sixième le furent en 75 et 80% et que les adolescents ont pu avoir été vaccinés à 40-50% à l'époque. On voit donc qu'il était indispensable de créer au moins 3 groupes et que faute de cela les études n'ont rien étudié du tout.
http://questionvaccins.canalblog.com/archives/2011/03/18/20609338.html
Pingback: Le paradoxe de Simpson | Apollo & Cie
Calculons l’intervalle de confiance à 95% de la proportion des groupes A et B par la méthode de Kott-Liu:
Groupe A : 273/350=78% : borne inférieure=73,4% borne supérieure=82,1%
Groupe B : 289/350=83% : borne inférieure=78,3% borne supérieure=86,3%
Ainsi il est très simple de constater, puisque les intervalles se chevauchent, que les résultats des groupes A et B ne peuvent pas être considérés comme différents, hypothèse de base de l’article.
Si c’est cela qui dérange Adrien il suffit de multiplier les nombres par 2 et vous aurez un écart plus que significatif entre les probabilités de guérison par A et par B.
Le vrai problème est donc ailleurs : c’est d’abord que le traitement A n’a pas la même probabilité de guérison sur les petits et les gros calculs (très significatif). Nommons p1 et p2 ces 2 probabilités. De même B n’a pas la même probabilité de guérison sur les petits et gros calculs (très significatif). Nommons les p’1 et p’2.
Comme p1 et p2 sont significativement très différents, la probabilité p de guérison des calculs, sans préciser la taille, n’existe pas ! De même la probabilité p’ de guérison par B n’existe pas ! Aussi, se demander si p=p’ n’a aucun fondement. c’est ce que j’avais essayé d’expliquer dans mon commentaire du 8 juillet 2014.
Pour travailler plus correctement on devrait tester séparément les hypothèses p1=p’1 et p2=p’2.
Si vous voulez une version avec des moyennes et non plus des proportions, voici : dans un panier de 10 choux il y a 3 choux bio à 2€ et 7 choux pas bio à 1€ soit 13€ le prix du panier, soit 1,30€ le prix moyen du choux. Dans un lot de 100 choux il y a 70 choux bio à 2€ et 30 à 1€ soit 1,70€ le prix moyen du choux.
Bien que les choux soient aux mêmes prix (au pluriel …), le prix moyen est beaucoup plus élevé dans le lot de 100. Le marchand accorde 10% pour prix de gros, ce qui ramène le prix moyen à 1,53€ qui est toujours beaucoup plus cher que le choux à 1,30€. Pourtant les choux dont le prix moyen est 1,53 sont 10% moins chers que ceux dont le prix moyen est 1,30€ !!! Ben oui, c’est comme ça et c’est tout simple !
Voilà le piège tout bête dans lequel nos épidémiologistes (entre-autres …) tombent tous les jours. Les fameuses études dites cas-témoins sont, par construction, soumises à ce risque (comparaison de la probabilité d’avoir été exposé à un médicament, à une pollution etc… chez les cas (les malades) et les témoins (non malades). Ces études déclarent souvent égales des probabilités … qui n’existent pas …
Dans l’exemple des calculs rénaux, les probabilités de guérison que Adrien a montrer égales, n’existent pas en réalité (il est statistiquement non acceptable de considérer que p1 et p’1 soient égales, moins d’une chance sur 1 million).
On peut y retrouver l’argumentaire des propriétaires de chiens mordants, à savoir :
Les labradors sont plus dangereux que les pitbulls car il y’a d’avantage de morsures/an dues aux labradors.
notes:
1) Est-ce que l’on ne devrait pas compléter (?) :
« UNE ANALYSE DU PARADOXE […] : 2 ingrédients:
– […] un facteur de confusion » (influent et ignoré),
– « Il faut que l’échantillon qu’on étudie ne soit pas distribué de manière homogène » notamment par rapport à ce facteur de confusion.
2) (Exemple 1)
Lorsqu’on tient compte du facteur de confusion (la grosseur des calculs
rénaux) et que l’on extrapole, relativement à ce facteur, des proportions de populations comparables pour l’effet de A et de B… l’effet paradoxal disparaît:
– population-test de A et extrapolation de la population-test de B:
taux de réussite global de A, tA : (87/350)x93%+(263/350)x73% = 78%
taux de réussite global de B, t’B : (87/350)x87%+(263/350)x69% = 73%
-> tA > t’B
– population-test de B et extrapolation de la population-test de A:
taux de réussite global de A -> t’A : (270/350)x93%+(80/350)x73% = 88%
taux de réussite global de B -> tB : (270/350)x87%+(80/350)x69% = 83%
-> t’A > tB
En fait, l’approche de ce genre de problème pourrait être très simple dans sa démarche fondamentale, sinon dans sa réalisation pratique. Si on reprend comme exemple celui des calculs rénaux on veut comparer 2 lois supposées a priori binomiales. L’exemple type serait : les pièces de 1 et 2 euros ont-elles une même probabilité de tomber sur pile ?
Pour ce faire il faut vérifier 5 conditions :
I- Le nombre de malades guéris par A suit-il une loi binomiale ? Soit 2 conditions pour cela :
1- les malades traités par A ont-t-il tous une même probabilité p de guérison ?
2- ces malades guérissent-ils de façon indépendante ?
II – Le nombre de malades guéris par B suit-il une loi binomiale ? Soit 2 conditions analogues avec une même probabilité p’ de guérison.
III – y-a-t-il indépendance entre la guérison des malades traités par A et ceux traités par B ? Cette dernière condition peut ne pas être toujours satisfaite dans les études type cas-témoins où l’exposition d’un futur cas et de ses futurs témoins peuvent ne pas être indépendantes. Cela se produit tout particulièrement quand le facteur d’exposition est un délai entre une vaccination et une maladie, les témoins pouvant avoir été vaccinés pratiquement en même temps que le cas auquel ils sont associés. En pareil cas il n’y a plus d’aléatoire par rapport au délai.
On a donc bien 5 conditions à vérifier. Si on peut accepter ces conditions, le test de comparaison de 2 binomiales sera fiable. C’est donc simple dans son principe.
Dans l’exemple des calculs rénaux les malades traités par A n’ont pas tous une même probabilité de guérison, ceux ayant des petits calculs ayant une probabilité de guérison estimée à 93% sur l’observation contre 73% pour les gros calculs, l’écart étant très significatif vu les effectifs. Le test global ne sera donc pas valable. Il conduit à accepter p=p’ alors que p n’existe pas !!!
Le recours aux facteurs de confusion contribue à créer la confusion. Il peut y avoir un facteur entrainant que p n’existe pas (la taille des calculs) et un facteur empêchant l’indépendance des guérison entre-elles. On a ainsi une liste de conditions qu’il faut chercher à vérifier. Ainsi la démarche. est claire dans ses objectifs et jalonnée dans sa recherche.
Bernard Guennebaud mathématicien
Pingback: Le paradoxe de Simpson | MYSQL | Scoop.it
Pingback: À ceux qui disent que dans les votes D. Trump n’a pas gagné – Carnet de notes
Bonjour,
Merci pour cet article très intéressant, et bien construit !
Je sais que le dernier commentaire a été posté il y a pas loin d’un an et demi, donc qu’il y a peu de chances pour que j’obtienne une réponse, mais ça ne m’aura dans le pire des cas que forcé à mettre par écrit une réflexion !
Voilà, ni dans votre article, ni dans les commentaires je n’ai vu apparaître l’idée de faire une Analyse en Composantes Principales (ACP). D’après mes maigres notions de stats et en tant qu’apprenti chercheur, je me dis qu’essayer d’identifier tous les facteurs de confusion d’une étude, puis « randomiser » l’échantillonnage pour les différentes conditions de l’expérience en fonction de ces facteurs supposés doit être assez compliqué à réaliser en pratique.
À l’inverse on pourrait envisager procéder à un échantillonnage certes plus conséquent, et plus détaillé (questionnaire à remplir par les participants), mais plus simple à mettre en place, suivi d’une ACP pour identifier les composantes ayant le plus d’impact sur la variable qui nous intéresse. Dans tous les exemples évoqués on verrait les facteurs de confusion ressortir avec un poids plus important que le facteur sur lequel porte l’étude, non ?
Et je ne sais pas vraiment ce qu’il est possible de faire à la suite d’une ACP, mais peut-être qu’il y a des options pertinentes dans le cadre de cette problématique ?
Voilà, c’est peut-être un raisonnement fallacieux, mais si c’est le cas je voudrais bien que quelqu’un éclaire ma lanterne en m’expliquant pourquoi ! 🙂
Bonne journée,
Thomas
Je vais donc répondre à Thomas C. Partant de l’exemple des calculs rénaux avec les 2 groupes A et B (2 traitements), le test initiale conduisant au paradoxe consiste en fait à comparer 2 lois binomiales, c’est à dire à tester si on peut accepter p=p’, p et p’ étant les probabilités de guérison par le traitement A et par le traitement B.
Comme je l’avais déjà expliqué, le paradoxe vient du fait que p et p’ n’existent pas ! Dans l’exemple les probabilités de guérisons par A ne peuvent être considérées comme étant les mêmes pour ceux ayant un gros calcul (73% de guérison) et pour ceux ayant un petit calcul (93% de guérison). Donc p n’existe pas !
De même pour B avec 87% de guérison pour les petits calculs contre 69% pour les gros. Donc p’ n’existe pas !
Le paradoxe vient du fait que l’on teste l’égalité p=p’ entre 2 probabilités qui n’existent pas !!!
Plus généralement il faudrait donc s’interroger sur l’existence de p et de p’ dans ce genre de tests de comparaison de 2 binomiales supposées. Ici la partition en petits et gros calculs est donnée, d’où une vérification par rapport à ce critère. Si on disposait que des données globales, 78% et 83% de guérison, on n’aurait aucune information permettant de faire une partition judicieuse. On serait alors contraint, si on veut être rigoureux, d’assortir la conclusion (on accepte p=p’) de la restriction :
« sous réserve que l’on puisse accepter que p et p’ existent, c’est à dire que l’on puisse considérer que tous les malades traités par A avaient la même probabilité de guérison et de même pour B. »
Si on dispose d’informations sur un sous groupe de A et sur son complémentaire, on peut alors étudier si ces 2 sous-groupes ont une même probabilité de guérisons. De même si on a des informations sur une partition A1, A2 …An et B1, … Bn. Si on doit accepter des probabilités p1, …pn différentes et de même p’1, …, p’n on testera séparément les égalités p1=p’1 …
Une ACP se réalise dans des conditions complètement différentes : à chaque individu considéré on associe par exemple 4 caractéristiques comme poids, taille, tour de taille, tour de cuisse. Pour chacun on a sa performance sur 100 mètres. On cherche alors par une ACP quel est le critère le plus pertinent en relation avec la performance. Ce pourrait par exemple être ici la taille et en second le tour de cuisse. On voit que les conditions d’une ACP n’ont rien à voir avec le test de comparaison de 2 binomiales quand celles-ci ne sont pas binomiales ! C’est cela et rien d’autres qui génère le (trop) fameux paradoxe
Bernard Guennebaud mathématicien
Pingback: Le paradoxe de Simpson — Science étonnante #7 – LightX
Pingback: Comment perdre un match en gagnant pourtant plus de points que son adversaire ! | Tennis Club de Westhouse
Pingback: Le paradoxe de Simpson met les statistiques sens dessus-dessous | Fact5
Pingback: Le paradoxe de Simpson — Science étonnante #7 | JetBip
Petite rectification:
Je me suis aperçu (avec …un certain retard,certes) en visualisant de nouveau cette vidéo, que les résultats de l’étude ne portent pas sur 1000 cas, mais sur 2000 en fait. Et là, on se rend compte que la lecture de ces résultats en est autrement plus faussée.
En effet, quand les médicaments guérissent 761 cas sur 1000, soit 76 %, ils guérissent,en fait,
761 cas sur 1000 cas traités avec les médicaments.
Et, idem pour la chirurgie qui guérit 658 cas sur 1000 cas traités par la chirurgie !
Donc, en fait, le médecin pourrait formuler que les médicaments guérissent 761 cas sur 2000, et la chirurgie 658 cas sur 2000. Ce qui nous donne un taux de guérison de 38,05 % pour les médicaments, et 32,9 % pour la chirurgie ! Ce qui n’est pas folichon pour rassurer le patient…
car le médecin peut dire que sur 2000 patients, le taux moyen de guérison est de … 35,48 %.
Alors qu’il en est tout à fait autrement : le taux de guérison des médicaments est de 76%, et celui de la chirurgie de 66%, quand on fait intervenir dans l’analyse un facteur externe, premier facteur de confusion, qui est le type de traitement , médicaments ou chirurgie.
Ensuite vient se rajouter le facteur de confusion que vous indiquez dans la vidéo, à savoir la taille de la tumeur.
On ne peut que constater la puissance de ce paradoxe de Simpson : on part d’un taux de guérison moyen à 35,48 % (ce qui n’est pas top, top); on rajoute un type de traitement, on tombe à 76 % pour l’un et 66 % pour l’autre, et quand on rajoute encore un facteur externe (la taille de la tumeur), on se rend compte que chacun des traitements guérissent à 82 et 90 %, ce qui est plutôt rassurant, alors qu’on était à 35,48 % de guérison dans la premier jet de conclusion. Et qu’en plus, ce facteur de confusion nous méprenait sur la détermination du traitement le plus efficace. Hallucinant !!!
Pingback: Triomphe des Lumières ou faillite de la raison ? | DBAO | Léo Varnet
Superbe article, je voulais le partager et le réexpliquer en réutilisant l’exemple de l’université, mais je n’arrive pas à identifier clairement le facteur de confusion. Je ne veux pas déformer le sens de l’article, quelqu’un peut-il m’éclairer ?
Un très bel exemple de paradoxe de Simpson sont les statistiques sur l’amélioration actuelle du taux de mortalité par le coronavirus : un facteur n’est pas pris en compte: les plus fragiles sont déjà décédés…
Oui, ou combien de décès y-a-t-il déjà eu. Et parmi eux, combien de plus fragiles ?
Les critères de fragilités n’étant pas clairement identifiés, reconnus et listés ( du moins au tout début de l’épidémie)
et quels sont les critères des « plus fragiles » ? Et combien sont -ils ?
j’aime bien le terme « randomisé » par c’est du franglais.
en vrai français, a-t-on un mot pour ce terme?
Bonjour,
» Hasardiser », peut-être ? Non, je ne pense pas qu’il y est d’équivalent, ni de synonyme. C’est un mot d’origine anglo saxonne (quelque peu technique, en plus) qui n’a pas assez « histoire » pour avoir un équivalent verbal en français. (même un synonyme).
Il y a « aléatoire », par exemple, et ses synonymes, mais ce n’est pas un verbe. J’avoue que j’avais eu du mal au départ; mais c’est vrai que ce mot franglais synthétise bien la description.
Bonjour,
Intuitivement, je dirais que c’est ce type de biais qui explique que certains présidents américains ont été élus alors qu’au total moins d’américains avaient voté pour eux, mais est-ce bien le cas?
Bravo pour toutes ces vidéos et ces billets, c’est vraiment de l’excellente vulgarisation, sans facteur de confusion possible! 😉 Merci!
Dans l’exemple de la tuberculose et de la streptomycine la randomisation avait été appliquée à 107 cas dont 52 non traités contre 55 traités pour démontrer son efficacité. Cette randomisation peut permettre de gommer les biais de sélection au sein des 107 cas retenus dans l’étude mais est évidemment sans effets sur les biais qui pourraient exister entre la population générale et la sélection de ces 107 cas. Je vais illustrer cela sur un exemple fabriqué à partir d’une situation réelle avec 2 traitements A et A’ pour traiter les calculs rénaux qui n’auront pas la même efficacité sur les petits et les gros calculs, ce qui peut être un facteur caché de confusion.
Ainsi, A aura une probabilité p1 de guérison des petits calculs et p2 pour les gros. De même A’ aura une probabilité p’1 pour guérir les petits calculs et p’2 pour les gros. On aura donc en réalité 4 inconnues. Un échantillon où l’on ne dissocie pas entre les petits et les gros calculs conduira à une équation (ou inéquation) avec 4 inconnues ce qui sera tout à fait insuffisant pour conclure que A et A’ seraient équivalents (ou différents), cette équivalence s’exprimant par p1=p’1 et p2=p’2. Il s’agit là d’une certitude mathématique que je vais illustrer numériquement.
Je prends p1=p’2=30 % et p2=p’1=70 % qui assure p1+p2=p’1+p’2. Mon échantillon sera constitué de 200 cas dont 100 petits calculs et autant de gros. Grâce à la randomisation j’aurai 2 échantillons de 100 cas avec 50 petits et 50 gros calculs dans chacun de ces 2 groupes. Le groupe traité par A donnera 50×30%+50×70%=50 guérisons. Celui traité par A’ donnera 50×70%+50×30%=50 guérisons. Je vais donc déclarer que les 2 traitements A et A’ sont équivalents alors qu’en réalité il n’en est rien ! Cette erreur peut conduire à des situations dommageables en pratique.
Ainsi, dans une population il y a 1000 cas dont 200 petits calculs et 800 gros. Si je traite par A j’aurai 200×30%+800×70%=620 guérisons alors que par A’ j’aurais 200×70%+800×30%=380 guérisons.
Comme la répartition des petits et gros calculs a toute chance d’être liée aux habitudes alimentaires très variables d’une région à une autre, on voit que l’affirmation fausse que les 2 traitements seraient équivalents ne sera pas sans conséquences. Mais peu importe ici. Cet exemple devrait suffire pour démontrer clairement que la randomisation à elle seule n’apporte aucune garantie d’élimination des biais de sélection entre la population générale et l’échantillon retenu pour procéder à la randomisation pourtant présentée comme un tampon officiel de garantie de qualité.
« En sciences, c’est pour cela que l’on préfère en général des expériences « randomisées », qui permettent d’assurer une distribution homogène : par exemple si vous avez des calculs rénaux et que vous participez à une expérience pour comparer les traitements, on vous assigne au hasard le traitement A ou B, sans que la taille des calculs influe sur la décision. On gomme ainsi l’inhomogénéité de distribution, et le paradoxe disparaît : le traitement A sera bien vu comme étant le meilleur. »
Je reprends les données du tableau avec 700 cas dont 270+87=357 petits calculs rénaux et 262+80=343 gros calculs. 350 cas tirés au hasard seront traités par A et autant par B. Pour répartir les petits et gros calculs dans les 2 groupes de 350 je m’autorise un écart d’un écart-type par rapport aux moyennes exactes, ce qui est parfaitement compatible avec les variations aléatoires.
Ainsi les 357 petits calculs se répartiront en 169 dans le groupe A et 188 dans B. La moyenne de 357 est 178.5 ; la variance s’obtient en divisant encore par 2 soit 89,25, l’écart-type étant la racine carrée 9,45 alors que 178,5-169=9,5. On aura donc 188 petits calculs dans B.
De même je répartis les 343 gros calculs en 162 dans A et 181 dans B. La moyenne de 343 est 171,5 ; la variance 85,75 et l’écart-type 9,26 avec 171,5-162=9,5.
Puis je prends les mêmes proportions de guéris avec A et B : 93 % de 169 vaut 157 ; 73 % de 162 vaut 118 soit 275 guéris par A parmi les 350 traités par A. 87 % de 188 vaut 164 ; 69 % de 181 vaut 125 soit 289 guéris par B.
CONSTAT : il y a davantage de guéris par B que par A alors que A est significativement plus efficace que B pour guérir les petits comme les gros calculs. Certes l’écart entre 289 et 275 rapporté à 350 n’est pas significatif mais vous voyez que votre affirmation n’était pas tout à fait exacte.
En fait, l’essentiel n’est pas la randomisation, contrairement à ce qu’on dit en médecine, mais la dissociation entre petits et gros calculs pour traiter par A et B 2 échantillons de petits calculs d’une part puis d’autre part pour traiter 2 échantillons de gros calculs. La randomisation peut alors s’effectuer au sein des 357 petits calculs pour les répartir entre A et B. Sur l’exemple on aura 169 petits calculs traités par A dont 157 guéris (93%) contre 188 traités par B dont 164 guéris (87%). Ainsi on verra la supériorité de A sur B.
MORALITE : il ne faut pas regrouper les petits et gros calculs ni croire qu’en effectuant la randomisation sur le cumul on peut éviter de dissocier et donc de connaître les facteurs de confusion. NON ! Il faut identifier ces facteurs de confusion et dissocier en fonction d’eux pour ne randomiser qu’après !
Bernard Guennebaud mathématicien
D’ailleurs les effets comparés des 2 traitements ne sont pas si différents que cela. En effet, ce qui est très significatif c’est le fait que le traitement A n’a pas du tout la même efficacité sur les petits et gros calculs et de même pour B :
Pour A on a 81 petits calculs guéris sur 87 contre 192 gros calculs sur 263 soit une chance sur 1 million d’avoir un tel écart par le seul fait du hasard.
Pour B on a 234 petits calculs guéris sur 270 contre 55 gros sur 80 soit 7 chances sur 10 000 par le hasard.
Si on compare les effets de A et B sur les petits calculs on trouve 3 % qui n’est pas significatif au seuil habituel (il faudrait moins de 2,5%).
Sur les gros on trouve 23,5 % qui n’est donc pas du tout significative. Sur ces observations on devrait au contraire accepter que A et B ont des effets comparables.
Ces calculs confirment qu’il n’est pas du tout adapté d’effectuer une randomisation sur le cumule des petits et gros calculs pour « démontrer » que A est supérieur à B alors que c’est faux sur les gros calculs et non significatifs sur les petits.
Ce que ces données montrent c’est que A et B traitent beaucoup mieux les petits calculs que les gros. Mais cela ne peut se voir qu’en dissociant et non pas en randomisant.
C’est la dissociation judicieuse qu’il faut promouvoir, la randomisation, une fois cette dissociation réalisée, n’étant qu’un petit appoint de détail.
Pingback: Le paradoxe de Simpson – Models&Code
Pingback: Comment juger une étude scientifique ? - La microkinésithérapie
Pingback: Paradoxe Simpson : – le petit blog des sciences