 Pour mesurer les distances dans l’Univers, les astronomes peuvent utiliser différentes méthodes, suivant qu’ils s’intéressent à des objets proches, comme les planètes du système solaire, lointains comme les étoiles, ou très lointains, comme les galaxies.
Pour mesurer les distances dans l’Univers, les astronomes peuvent utiliser différentes méthodes, suivant qu’ils s’intéressent à des objets proches, comme les planètes du système solaire, lointains comme les étoiles, ou très lointains, comme les galaxies.
Mais ces différentes méthodes ne sont pas indépendantes, et elles reposent en fait les unes sur les autres : il faut d’abord connaître les distances aux objets les plus proches pour pouvoir déduire correctement celles des objets les plus lointains.
Cette hiérarchie de méthodes s’appelle l’échelle des distances cosmiques, et nous allons voir qu’elle permet de passer de la connaissance de la taille d’un simple bâton, à celle de l’Univers visible !
De la Terre à Mars
 La méthode la plus importante en astronomie s’appelle la méthode de la parallaxe. Elle se base sur un principe simple : si on se déplace légèrement par rapport à un objet, son mouvement apparent sera d’autant plus important que l’objet est proche. On connait bien cela sur les (vieux) jeux vidéos, où la vitesse de défilement du décor nous renseigne sur son éloignement.
La méthode la plus importante en astronomie s’appelle la méthode de la parallaxe. Elle se base sur un principe simple : si on se déplace légèrement par rapport à un objet, son mouvement apparent sera d’autant plus important que l’objet est proche. On connait bien cela sur les (vieux) jeux vidéos, où la vitesse de défilement du décor nous renseigne sur son éloignement.
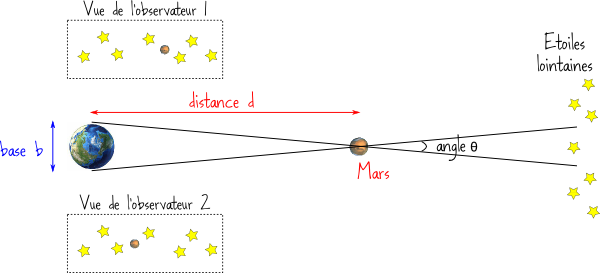
Ainsi en astronomie, on peut essayer d’observer une planète depuis deux endroits différents de la Terre. Comme l’illustre le schéma ci-dessous (très exagéré), la position de Mars par rapport au fond formé par les étoiles lointaines variera légèrement quand on passe d’un côté à l’autre de la Terre.
De ces observations on peut déduire la distance entre la Terre et Mars, il suffit de faire un peu de géométrie. Tout d’abord il faut connaître la distance de base \(b\) entre les deux points d’observation (ici le diamètre de la Terre). Ensuite on mesure l’angle \(\theta\) entre les deux positions que prend notre objet vu depuis chacun des deux points d’observation. On peut ensuite déduire la distance \(d\) avec la simple relation \(d = b/\theta\).
En pratique ça n’est pas si simple car l’angle à mesurer entre les deux positions est minuscule, au plus quelques centièmes de degrés. Soit la taille qu’aurait un cure-dent vu à un kilomètre de distance ! Et puis autre problème, pour que la méthode soit précise, il faut bien connaitre le diamètre de la Terre. Oh mais ça c’est facile, je vous l’ai expliqué dans ce billet : Erathostène l’avait mesuré à partir d’un simple bâton et de quelques chameaux !
Les deux premiers barreaux de l’échelle cosmique nous font donc passer de la taille d’un bâton à celle de la Terre, puis de celle de la Terre à la distance qui nous sépare de Mars !
De Vénus au Soleil
En principe, cette méthode devrait nous permettre aussi de calculer directement la distance au Soleil. Le problème du Soleil, c’est qu’en plein jour on ne voit que lui, et qu’il est donc impossible de mesurer la variation d’angle. Il faut donc ruser un peu.
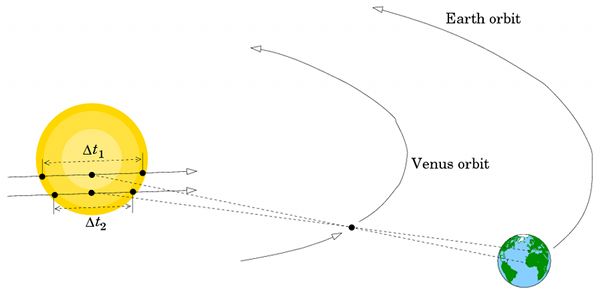
Pour cela, on peut utiliser les transits de Vénus, ces moments où Vénus passe pile-poil devant le Soleil. Il faut bien viser car ils ne se produisent que très rarement (le prochain sera en 2117). En mesurant la différence entre les transits vus depuis deux points d’observation différents, on applique la méthode de la parallaxe et on en déduit la distance Terre-Vénus (au moment cette dernière est pile entre le Soleil et nous.)
Puis on utilise une loi astronomique, qui relie P la période de l’orbite d’un astre à sa distance D au Soleil
\(P \propto \sqrt{D^3}\)
En connaissant la période de la Terre (365 jours) et celle de Vénus (seulement 225 jours), on peut en déduire la distance Terre-Soleil, qui vaut environ 150 millions de kilomètres. C’est notre troisième barreau !
Du Soleil aux étoiles
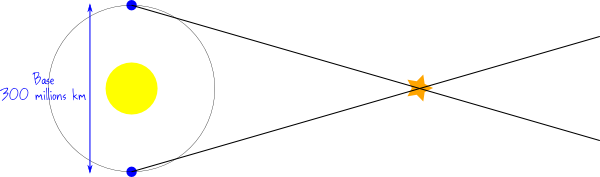
Maintenant que l’on connait la distance Terre-Soleil, on peut exploiter cette information et grimper un peu plus haut dans l’échelle des méthodes. Il suffit en effet de reprendre le principe de la méthode de la parallaxe, mais en utilisant non pas deux points d’observation sur la Terre, mais deux observations faites à 6 mois d’écart. Dans ce cas la Terre se sera déplacée de deux fois la distance Terre-Soleil, et on pourra appliquer la méthode avec une base de 300 millions de km au lieu des 12 000 km du diamètre terrestre. Nous avons donc gagné un facteur 25 000 !
C’est cette méthode qui permet de mesurer la distance aux étoiles les plus proches. On compte d’ailleurs parfois les distances astronomiques en « parsecs », c’est-à-dire « une seconde de parallaxe ». Si la variation de parallaxe est d’une seconde d’arc, c’est à dire 1/3600e de degré, on peut calculer que l’objet est à environ 3.26 années lumière. C’est en gros la distance à notre étoile la plus proche, alpha du Centaure.
Comme les angles à mesurer sont minuscules, cette méthode ne fonctionne malheureusement que pour les étoiles les plus proches. La limite se situe autour de quelques centaines d’années lumières, ce qui est vraiment la proche banlieue du Soleil, puisque notre galaxie la Voie Lactée fait environ 100 000 années lumières de diamètre. Donc pour aller plus loin, il va falloir encore trouver une autre méthode !
Des étoiles aux galaxies
Si vous vous promenez dans la nuit et que vous voyez une voiture arriver au loin, vous pouvez juger de sa distance approximative à partir de la luminosité de ses phares. Si elle est très loin, l’éclat sera faible; alors que si elle est proche, les phares vous éblouissent. C’est le principe de la chandelle standard : si on observe un objet dont on connait la luminosité intrinsèque, alors sa luminosité apparente nous renseigne sur sa distance.
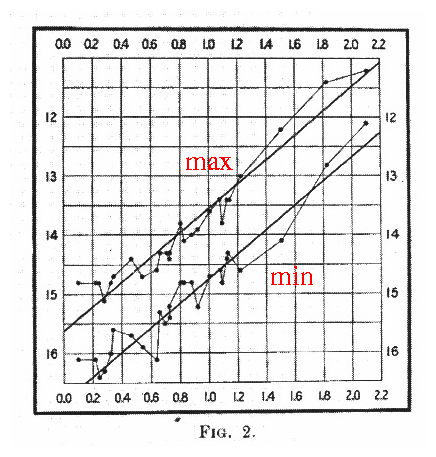 Oui mais dans l’espace, comment on trouve des objets dont on connait la luminosité intrinsèque, puisqu’on ne peut pas s’approcher d’eux pour les observer ? Eh bien c’est possible grâce à une découverte étonnante : les Céphéides. Ces étoiles sont ce qu’on appelle des étoiles variables, dont l’éclat oscille en fonction du temps, avec des périodes de quelques jours. Or ce qu’a découvert l’astrophysicienne Henrietta Leavitt au début du XXème siècle, c’est que leur période d’oscillation est reliée à leur luminosité. Le graphique ci-contre représente les données de Leavitt (en échelle log/log, avec le min et le max de luminosité de chaque étoile)
Oui mais dans l’espace, comment on trouve des objets dont on connait la luminosité intrinsèque, puisqu’on ne peut pas s’approcher d’eux pour les observer ? Eh bien c’est possible grâce à une découverte étonnante : les Céphéides. Ces étoiles sont ce qu’on appelle des étoiles variables, dont l’éclat oscille en fonction du temps, avec des périodes de quelques jours. Or ce qu’a découvert l’astrophysicienne Henrietta Leavitt au début du XXème siècle, c’est que leur période d’oscillation est reliée à leur luminosité. Le graphique ci-contre représente les données de Leavitt (en échelle log/log, avec le min et le max de luminosité de chaque étoile)
Les Céphéides peuvent donc servir de chandelles standard, puisque leur luminosité intrinsèque se déduit de leurs oscillations. Comme ces étoiles sont assez brillantes et faciles à repérer, on a pu les utiliser pour mesurer des distances jusqu’à 100 millions d’années lumières, c’est-à-dire toute la Voie Lactée mais aussi les galaxies les plus proches !
Petit détail d’extrême importance : pour que la relation découverte par Leavitt soit utilisable, il faut la calibrer, c’est-à-dire disposer d’au moins une étoile de type Céphéide dont on connaisse la distance par une autre méthode. Il se trouve que l’une des plus proches, delta-Cephei n’est qu’à 900 années lumières de nous, et est donc aussi mesurable par la méthode de la parallaxe. Vous voyez encore l’effet d’échelle : c’est parce que la méthode des parallaxes fonctionne que l’on peut construire celle des Céphéides pour aller plus loin !
Jusqu’aux confins de l’Univers
Pour aller encore plus loin et mesurer les distances aux galaxies lointaines, il faut à nouveau changer de méthode car les Céphéides ne sont plus assez brillantes pour être observées. Heureusement d’autres objets astrophysiques exceptionnels peuvent servir de chandelles standard : les supernovas.
Les supernovas sont des étoiles qui explosent de manière ultraviolente dans des conditions rares mais bien définies. Quand cela se produit, on sait exactement quelle sont l’énergie et la luminosité dégagées, et l’explosion peut donc servir de chandelle standard. Contrairement aux Céphéides, il s’agit d’un événement ponctuel qui ne se produit pas souvent. Mais en surveillant des tas de galaxies à la fois, on peut en repérer une de temps en temps et déduire ainsi les distances aux galaxies les plus lointaines. D’autant que leur éclat peut persister assez longtemps, comme le montre l’image ci-dessous prise par le télescope Hubble, et où l’on voit une supernova ayant explosé en 1987.
Si vous m’avez suivi jusque là, vous aurez remarqué combien l’édifice est subtil, car chaque méthode utilise des résultats de la précédente : le diamètre de la Terre permet de connaître la distance Terre-Soleil, celle-ci permet de calibrer la méthode des Céphéides, qui elle-même sert de calibration à celle des supernovas. Voilà donc pourquoi pourquoi on parle d’échelle cosmique des distances.
Voir aussi mon billet « Il y a bien longtemps, dans une galaxie lointaine, très lointaine… »
Pour aller plus loin
Vu l’imbrication qui existe entre ces différentes méthodes, on comprend que les astronomes passent encore beaucoup de temps à mesurer la distance qui nous sépare d’objets pourtant proches. Car toute erreur sur une méthode « de base » se propage sur les autres. Ainsi aujourd’hui la distance à Vénus est mesurée par des méthodes radars : on calcule le temps mis par un signal pour aller et revenir.
Tout récemment, une équipe a présenté une nouvelle mesure de la distance qui nous sépare du grand nuage de Magellan [1], qui est une sorte de galaxie naine (visible dans l’hémisphère sud) et qui n’est qu’à 150 000 années lumières. Cet objet est de grande importance, car c’est ce que nous avons de mieux pour calibrer la relation période-luminosité des Céphéides ! En réduisant à 2% la barre d’erreur, on améliore la calibration de toutes les autres méthodes, et par là-même la précision de la mesure de la constante de Hubble, qui elle-même détermine les prédictions cosmologiques les plus folles, comme celles portant sur la matière noire ou la forme et le destin de l’Univers !
Vous pouvez en apprendre plus sur ce papier grâce au billet d’Eric Simon sur le site Ça se passe là haut, un très bon site d’astro, et nouveau venu au C@fé des Sciences !
[1] Pietrzyński, G., et al. « An eclipsing-binary distance to the Large Magellanic Cloud accurate to two per cent. » Nature 495.7439 (2013): 76-79. arxiv:1303.2063





Comments
Avant meme de lire cet article, je lui associe ce Memo : http://0z.fr/R4xBq
Maintenant, je ne manquerai pas de vous lire.
Bien a vous…
»Donnez-moi un point d’appui et je souleverai le monde »
Cette phrase attribuee a Archimede me semble illustrer assez bien le contenu de cet article. Nous sommes dans l’illusion car la constance de Hubble n’en est pas une. Cela me fait penser a ces astrophysiciens qui pretendent qu’il n’y a pas de centre de l’Univers, que le centre est partout. Ils sont encore loin d’avoir compris les forces en presence et leurs relations.
Bien a vous….
Bonjour,
Pour répondre à Kristen Chaman :
Tout dépend à quel niveau on se situe : physique ou spirituel.
Tout appuis physique n’étant qu’illusion de concept de la pensée.
Bonjour,
Merci pour la référence. Très belle vulgarisation d’un sujet pas très simple à expliquer clairement. J’ai une petite remarque de terminologie : Le pluriel de supernova est par usage le pluriel latin : supernovae.
Par ailleurs j’ai vu écrit le mot « constance » de Hubble, il s’agit bien sûr de « constante », même si il est vrai qu’à l’échelle des temps cosmiques, le facteur de proportionnalité entre vitesse de récession et distance varie, H0 est ce facteur au temps présent et est bien constant… en 2013, il vaut la même chose qu’en 1929, et la même chose qu’en 3146 ou en -400… Sa variation se voit sur des échelles de temps très grandes….
Oups, bien vu pour la faute de frappe, il s’agissait bien sûr de la constante de Hubble ! (dont on connait la non-constance :-))
Quant au pluriel de supernova, j’avoue que je me suis posé la question…et puis j’ai décidé de faire comme « scenario », vu que l’Académie accepte le pluriel francisé (scénarios que je trouve moins snob que scenarii !), je me suis autorisé à faire pareil. Bien que je doute que l’Académie se soit penché sur le cas des supernova-e-s !
Eh bien je viens de vérifier…en fait l’Académie Française s’est bel et bien penchée sur le pluriel de « supernova » dans sa réforme de 1990 ! Incroyable !
http://fr.wiktionary.org/wiki/Annexe:Rectifications_orthographiques_du_fran%C3%A7ais_en_1990
On y découvre aussi le pluriel de « un superman », qui est donc « des supermans ».
Bonjour,
merci pour votre blog. Il est tres instructif et votre effort pour faciliter la comprehension des choses tres scintifiques est formidable.
J’ai lu recemment que l’etoile la plus proche est Proxima Centaure.
Non ! C’est la seconde étoile la plus proche de la Terre ; la première étant le soleil.
Pingback: La renaissance du temps article 7 (Lee Smolin Partie II chap. 14) | Thomassonjeanmicl's Blog
Ancien professeur de mathématiques, j’ai conçu un nouveau modèle cosmologique selon lequel notre univers est une onde qui se propage à la surface d’une boule de rayon R d’un espace physique à 5 dimensions.
Ce modèle (3e infini) permet le calcul de la distance actuelle d’une source lumineuse quelconque S en fonction de son décalage spectral Z, de l’âge de l’univers et du rayon R.
Pour toute source lumineuse, on peut donc calculer une valeur de la constante de Hubble H si l’on connait la valeur de R. Plusieurs raisons m’ont amené à choisir R = 37. Les résultats sont surprenants : pour les distances inférieures à environ 1500 Mpc, on trouve des valeurs de H différant de moins de 2% du nombre 67,8.