 C’est en cours de philo que j’en ai entendu parler pour la première fois ! Notre prof nous faisait un cours sur la logique et ses fondements, et c’est alors qu’elle le mentionna : le fameux théorème de Gödel, celui qui prouve que quoi qu’on fasse, il existe des énoncés mathématiques vrais, mais indémontrables. Les mathématiques resteront à tout jamais un édifice imparfait !
C’est en cours de philo que j’en ai entendu parler pour la première fois ! Notre prof nous faisait un cours sur la logique et ses fondements, et c’est alors qu’elle le mentionna : le fameux théorème de Gödel, celui qui prouve que quoi qu’on fasse, il existe des énoncés mathématiques vrais, mais indémontrables. Les mathématiques resteront à tout jamais un édifice imparfait !
J’en fus évidemment tout retourné et fasciné : comment était-il possible qu’un truc pareil existe ? Comment prouver ce résultat pouvait même être du domaine de la science ?
Peut-on tout démontrer en mathématiques ?
Quand on fait des mathématiques, on manipule des énoncés. Un énoncé est une suite de symboles ou une phrase ayant un sens mathématique précis. Par exemple 2 + 2 = 4 ou « Il existe une infinité de nombres premiers » sont des énoncés mathématiques. Un énoncé mathématique est soit vrai, soit faux : par exemple 2 + 2 = 5 est un énoncé faux.
Quand on considère un énoncé mathématique, on ne sait pas forcément à l’avance s’il est vrai ou faux. Le travail du mathématicien, c’est justement d’essayer de savoir lesquels sont vrais et lesquels sont faux. Et pour cela, il utilise un outil : il fait des démonstrations.
Si un mathématicien arrive à démontrer un énoncé, on considère que cet énoncé est « vrai ». S’il démontre le contraire, alors on dit que l’énoncé est faux.
Les mathématiques reposent donc sur l’idée que si un énoncé est vrai, alors il doit en exister une démonstration, et il n’y a plus qu’à la trouver. Mais est-on sûr que tout ce qui est « vrai » est forcément « démontrable » ? Se pourrait-il qu’il existe des choses vraies mais indémontrable ?
Notez bien que s’il existe des choses vraies mais indémontrables, c’est un camouflet pour les mathématiciens, car cela signifie qu’il y a des questions mathématiques auxquelles ils ne peuvent pas répondre ! Pour couper court à cette inquiétude, au début du XXème siècle, quelques matheux et logiciens menés par David Hilbert ont voulu asseoir les maths sur des bases inattaquables. Ils ont donc cherché à montrer que si une affirmation mathématique est vraie, alors il en existe nécessairement une démonstration.
Malheureusement pour eux, en 1931, le jeune logicien tchèque Kurt Gödel a douché leurs espoirs avec un résultat aussi diabolique qu’inattendu : en mathématique, il existera toujours des énoncés vrais, et pourtant indémontrables. Même sur leur propre terrain de jeu, les maths ne sont donc pas toutes puissantes !
Mais pour comprendre exactement de quoi il retourne, il nous faut creuser un peu la notion de « démontrable ».
A quoi jouent les mathématiciens ?
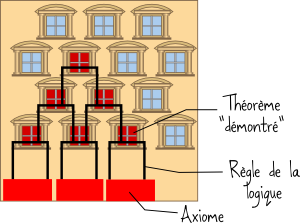 Pour démontrer des choses, les matheux utilisent ce qu’on appelle la méthode axiomatique. Ils se donnent certaines affirmations comme ingrédients de départ : ce sont les axiomes. Puis ils cherchent à les combiner selon les règles de la logique pour essayer d’aboutir à de nouvelles affirmations. Une affirmation déduite des axiomes est considérée comme « démontrée » (on peut alors la qualifier de théorème).
Pour démontrer des choses, les matheux utilisent ce qu’on appelle la méthode axiomatique. Ils se donnent certaines affirmations comme ingrédients de départ : ce sont les axiomes. Puis ils cherchent à les combiner selon les règles de la logique pour essayer d’aboutir à de nouvelles affirmations. Une affirmation déduite des axiomes est considérée comme « démontrée » (on peut alors la qualifier de théorème).
Pour illustrer le principe de la méthode axiomatique, on peut utiliser une analogie avec un échafaudage. Les axiomes, ce sont les bases de notre échafaudage, et les règles de la logique nous permettent de monter une structure qui repose sur ces axiomes. Chaque fenêtre à laquelle on accède grâce à notre échafaudage est une affirmation démontrée qui devient un théorème.
Toutes les mathématiques se font au moyen de la méthode axiomatique, mais il existe plusieurs choix possibles pour les axiomes. Si vous voulez faire de la géométrie dans le plan, vous allez partir des axiomes d’Euclide. Si vous avez envie de considérer uniquement les nombres entiers, vous pouvez vous tourner vers les axiomes de l’arithmétique de Peano. Pour vous faire une idée de ce à quoi ça ressemble, voici quelques uns de ces axiomes :
- 0 est un nombre
- Tout nombre possède un suivant
- 0 n’est le suivant d’aucun nombre
- Si x=y et y=z, alors x=z
- etc.
Enfin si vous voulez faire des maths plus subtiles, vous devez utiliser un système d’axiomes plus travaillé. Aujourd’hui, LE système d’axiomes sur lequel reposent toutes les mathématiques modernes, c’est celui de la théorie des ensembles de Zermelo-Frenkel (noté ZFC pour les intimes). Ça veut dire que si de nos jours un mathématicien dit « J’ai démontré ceci », alors c’est sous-entendu « en utilisant les axiomes de ZFC ».
Ce que dit le théorème de Gödel
 Nous avons vu que la notion de « démontrabilité » est toujours relative à un système d’axiomes. Cela veut dire qu’une certaine affirmation mathématique peut très bien être démontrable avec un système, mais pas avec un autre ! Ce dont ont voulu s’assurer Hilbert et sa bande au début du XXème siècle, c’est qu’il était possible de construire un système d’axiomes parfait, tel que toutes les propositions mathématiques vraies y soient démontrables. Un tel système serait dit « complet ».
Nous avons vu que la notion de « démontrabilité » est toujours relative à un système d’axiomes. Cela veut dire qu’une certaine affirmation mathématique peut très bien être démontrable avec un système, mais pas avec un autre ! Ce dont ont voulu s’assurer Hilbert et sa bande au début du XXème siècle, c’est qu’il était possible de construire un système d’axiomes parfait, tel que toutes les propositions mathématiques vraies y soient démontrables. Un tel système serait dit « complet ».
Et c’est précisément cet espoir que Gödel a ruiné : il a démontré que dès que l’on veut faire au minimum de l’arithmétique des nombres entiers, quel que soit le système d’axiomes qu’on utilise, il existera toujours des énoncés vrais mais indémontrables. On dit que ces énoncés sont indécidables.
Cela signifie qu’il n’existe pas de système d’axiomes complet, et c’est pour cela que l’on appelle ce théorème, le théorème d’incomplétude.
Pour reprendre l’analogie avec l’échafaudage, on peut y mettre autant de piliers qu’on veut, il existera toujours des fenêtres de l’immeuble qu’on ne pourra pas atteindre !
Les implications pratiques du théorème de Gödel
En théorie, le théorème de Gödel est une catastrophe. Il nous dit que, aussi sophistiqués et nombreux que soient nos axiomes de départ, on va se retrouver avec des énoncés indécidables. Cela veut dire qu’il y a peut être des milliers de mathématiciens en train de passer leurs journées à chercher des démonstrations … de choses indémontrables !
Heureusement, en pratique, presque tout le monde se fiche du théorème de Gödel. En effet on s’est rendu compte que malgré tout, les propositions indécidables sont tellement tordues qu’on ne les croise pour ainsi dire jamais, et donc la quasi-totalité des propositions vraies « normales » sont démontrables avec les systèmes d’axiomes qu’on utilise. On est donc convaincus que l’on dispose de suffisamment de bon piliers à notre échafaudage pour atteindre toutes les fenêtres intéressantes.
Ainsi si aujourd’hui un mathématicien lambda cherche à faire une démonstration, sa principale crainte sera de ne pas être assez fort pour la trouver. Mais presque à aucun moment il n’envisage sérieusement que cette proposition soit « indémontrable ». Les conséquences pratiques du théorème de Gödel sont donc très limitées.
Une saveur de la démonstration
Je ne voudrais pas passer trop de temps à parler de la démonstration proprement dite. D’une part on la trouve décrite un peu partout d’autre part je trouve que c’est ce qui obscurcit souvent les présentations vulgarisées du théorème. Ceux qui ont mal à la tête peuvent arrêter là ! (N’oubliez pas que Gödel est mort fou, tout comme d’autres logiciens ayant traité des questions similaires comme Cantor, Zermelo, Post, Frege, Wittgenstein…enfin d’après Logicomix)
Pour démontrer son diabolique théorème, Gödel fait essentiellement une preuve « constructive » : il donne une recette pour fabriquer plus ou moins explicitement un énoncé arithmétique indécidable, et ce quel que soit le système d’axiomes de départ. Pour se faire une idée de ce dont il s’agit, Gödel mime en quelque sorte le paradoxe du menteur.
Vous connaissez certainement ce paradoxe, c’est celui d’un Crétois qui affirme « Tous les Crétois sont des menteurs ». Mais alors, lui-même dit-il la vérité à ce moment précis ? Une variante encore plus compacte de ce paradoxe, c’est l’énoncé « Cette phrase est fausse ». Alors, est-elle fausse…ou vraie ?
Le principe de la démonstration de Gödel, c’est de construire un énoncé qui dit « Je ne suis pas démontrable ». Vous voyez que si cet énoncé est vrai, alors…il n’est pas démontrable. Il est donc bien « indécidable » et le système d’axiomes est bien « incomplet ». En revanche si cet énoncé est faux, alors il est démontrable, et là c’est la catastrophe : on a un système d’axiomes qui démontre des choses fausses ! On dit que le système est inconsistant. D’ailleurs pour être précis, ce qu’a démontré Gödel, c’est qu’un système d’axiomes (contenant au moins l’arithmétique) est soit incomplet, soit inconsistant. Pas d’autre alternative.
Dans le détail, la démo repose sur une idée conceptuelle géniale, et sur une astuce diabolique.
L’idée conceptuelle géniale, c’est celle de la réflexion arithmétique des propositions méta-arithmétiques. Qu’est-ce que ça veut dire ? Si je dit « 2 + 2 = 4 », je fait un énoncé arithmétique. Si je dis « 2 + 2 = 4 est démontrable à partir des axiomes de Peano », je fais un énoncé « méta-arithmétique ». L’idée géniale de Gödel, c’est d’arriver à lier les deux. En gros il a montré que :
Pour tout énoncé E, il existe un autre énoncé S(E) tel que : E est démontrable si et seulement si S(E) est vrai.
Ce travail se fait au moyen d’une méthode de codage qui permet de transformer tout énoncé en un nombre entier et toute démonstration en une suite de nombres entiers. La démontrabilité de E se traduit donc comme une propriété arithmétique sur des suites de nombres, c’est l’énoncé S(E). Ensuite l’astuce diabolique, c’est ensuite de trouver UN énoncé particulier, noté G, tel que « S(G) = non-G ». En appliquant le résultat précédent pour cet énoncé particulier G, on obtient alors l’affirmation
G est démontrable si et seulement si G est faux.
Donc soit G est vrai et il est donc indémontrable (et on a l’incomplétude), soit il est faux et démontrable (et on a l’inconsistance). Une fois de plus, si vous vous intéressez aux détails de cette démonstration, il faut creuser un peu plus et il y a plusieurs endroits où c’est décrit (par exemple ici).
Pour aller (vraiment) plus loin…
Pour ceux qui ont tenu jusque là et qui se posent quelques questions métaphysiques, voici quelques pistes de réflexion, sur des choses au sujet desquelles je ne suis moi même pas très à l’aise. Commentaires les bienvenus !
Pour commencer, il existe quand même quelques exemples de propositions indécidables et à peu près compréhensibles. Par exemple le théorème de Goodstein, qui concerne des simples suites de nombres (un peu comme la conjecture de Syracuse) : il est indécidable dans l’arithmétique de Peano, mais heureusement démontrable dans la théorie ZFC.
Un exemple plus sophistiqué, c’est le problème de Whitehead : c’est un énoncé de théorie des groupes pas trop difficile à comprendre (après le bac quand même), et pourtant indécidable même dans ZFC ! De même, un des exemples les plus connus est l’hypothèse du continu : existe-t-il un ensemble de nombres qui soit « plus grand » que N mais « plus petit » que R ? C’est indécidable !
Enfin, si on utilise la théorie des ensembles de Zermelo-Frenkel au sens strict (notée ZF), alors il existe un énoncé indécidable qu’on appelle l’axiome du choix. On choisit en général de l’ajouter à la liste des axiomes de ZF, pour obtenir la théorie ZFC.
Autre point pour ceux qui veulent creuser : Gödel a démontré un deuxième théorème d’incomplétude ! Le premier théorème dit que tout système est soit incomplet, soit inconsistant. L’incomplétude est un problème, mais l’inconsistance est une catastrophe ! On aimerait donc pouvoir s’assurer qu’un système donné est incomplet plutôt qu’inconsistant. Ce que dit le deuxième théorème, c’est qu’on ne peut pas démontrer la consistance d’un système formel en restant à l’intérieur de celui-ci.
Il y a quelque chose qui m’a longtemps troublé avec cette idée de propositions indécidables. Si on obtient une proposition vraie mais indécidable, alors on peut décider de l’ajouter comme axiome. Rien de bien troublant. Mais on peut aussi très bien décider d’ajouter son contraire à notre liste d’axiomes. Puisque la proposition est indécidable, on ne crée pas d’inconsistance. Mais qu’est-ce qu’on obtient si on fait ça ? Un système d’axiomes dont un axiome est une proposition « fausse ». N’est-ce pas paradoxal ?
Pour résoudre la difficulté, il faut creuser la notion de « vrai ». J’ai insisté sur le fait que la notion de « démontrable » était relative à un système d’axiomes. Par contre je suis passé vite sur la notion de « vrai », comme si elle était universelle et intrinsèque. En fait elle ne l’est pas, elle est relative à ce qu’on appelle un « modèle ». Pour l’arithmétique, il n’y a pas trop de débat sur quel est le modèle. Mais par exemple pour la géométrie, il y a plusieurs choix ! Le modèle classique est celui de la géométrie euclidienne. Pour trouver un système d’axiomes qui colle avec ce modèle, il faut prendre le 5ème axiome d’Euclide dans sa forme familière (une seule parallèle à une droite passe par un point donné). Mais si vous changez de modèle, par exemple la géométrie riemannienne, il vous faut un autre système d’axiomes qui va bien, et que l’on peut obtenir en modifiant le 5ème axiome (aucune parallèle ne passe par un point donné).
Donc si on choisit d’ajouter aux axiomes de Peano une proposition indécidable fausse, on obtient un système d’axiomes qui ne représente plus correctement l’arithmétique. Si j’ai bien compris, on peut considérer à la place des modèles d’arithmétique « non-standard », mais dont j’imagine que l’intérêt est limité (contrairement à la géométrie, où les modèles non-euclidiens ont un intérêt physique).
Mais pour les mathématiques de la théorie des ensemble, quel est le modèle raisonnable qui nous dit ce qui est vrai et ce qui est faux ? Une solution serait le modèle de l’Univers Constructible de Gödel, dans lequel l’axiome du choix (comme l’hypothèse du continu) sont « vrais » … mais je ne suis pas sûr de comprendre pourquoi !
Si vous êtes très malin, vous avez peut être eu l’idée de trouver un contre-exemple au théorème de Gödel et de construire un système d’axiomes parfait de la manière suivante : prendre toutes les propositions vraies, et les déclarer toutes « axiomes ». Même si ça n’est pas très intéressant en pratique, ça semble échapper à Gödel. La raison en est que Gödel suppose un système d’axiomes « récursivement énumérable » récursif. Cela signifie que les axiomes ont le droit d’être en nombre infini, mais il doit exister une procédure « finie » pour décider si une proposition donnée fait partie des axiomes ou non. Un système d’axiomes qui ne soit pas récursif n’a aucun intérêt pratique, puisqu’on ne peut jamais vérifier en temps fini si quelque chose est un axiome !
Enfin dernier point, les conséquences informatiques du théorème de Gödel sont souvent discutées (voire on trouve parfois le théorème énoncé sous cette forme) : la première conséquence, c’est qu’il n’existe pas de programme qui puisse dire si une proposition donnée est un théorème ou non. Une autre conséquence reliée, c’est qu’il n’existe pas de programme qui puisse dire avec certitude si un autre programme va terminer en temps fini, ou non (voir ici).
Bon j’ai largement dépassé 2000 mots, j’arrête. Vous pouvez reprendre vos activités normales !


143 Comments
Pingback: vincent_voisin (vincent_voisin) | Pearltrees
Supposons qu’une proposition P ne soit pas décidable dans PA (axiome de Peano) mais se démontre dans ZF (par exemple le théorème de Goodstein). Est-ce que cela implique que P est vraie dans PA ?
Plus généralement, pour montrer qu’une proposition P est vraie dans une théorie T, est-il suffisant de démontrer P dans une théorie T’ contenant T (où l’on a rajouté disons un axiome indécidable dans T)?
« Vraie dans PA » n’a pas de sens, il y a juste des énoncés démontrables dans PA, d’autres dont on peut montrer la négation dans PA, et d’autres indécidables dans PA. La notion de « vrai » est liée à un modèle. Si P est indécidable dans PA, il y a des modèles de PA où P est vraie et d’autres où P est fausse.
Merci pour ta réponse Denis ; comme je ne suis pas spécialiste de ce domaine, poser une question est difficile…. Je précise un peu ma question avec l’exemple de Goodstein. Le fait de l’avoir démontrer dans ZF, est-ce que cet énoncé est vrai dans N standart en oubliant les axiomes ZF ?
Avec plaisir 🙂 Oui effectivement c’est bien le cas: puisque N standard est un modèle de ZF (en tout cas la partie « arithmétique » de ZF), tout ce qu’on peut prouver dans ZF est vrai dans N. En particulier il est bien vrai « en pratique » que les suites de Goodstein s’arrêtent toujours peu importe le point de départ, il faut juste s’armer de patience. Pour résumer, on peut dire que ZF est un outil plus puissant que PA pour prouver des choses sur N.
Salut David, dans la partie « saveur de la démonstration » sur quoi est ce qu’on se base pour affirmer qu’un énoncé est vrai ? le fait que cette énoncé est justement démontré dans le système d’axiome n’indique t-il pas que ceci est vrai ou du moins cohérent avec ce système.
pourrait on appliquer ce théorème à une autre science tel que la biologie?
C’est un des trucs que je n’ai pas mentionné : on fait souvent dire tout et n’importe quoi au théorème de Gödel, en essayant de l’appliquer là où il n’y a pas lieu.
« on ne sera jamais sur de rien » (gödelite aigüe) est assez dans la tendance « tout est relatif » (einsteinite aigüe)
Donc la réponse est : non 🙂 Le théorème de Gödel s’applique uniquement dans un cadre très precis : les systèmes formels basés sur un système d’axiomes récursivement énumerables contenant l’arithmetique.
Ce n’est pas la peine de préciser « basés sur un système d’axiomes RE » : la notion de système formel inclut déjà cette propriété. D’autre part, pas besoin de contenir l’arithmétique. De plus, les systèmes formels sont omniprésents en science, donc le « cadre très précis » est en réalité assez vaste.
Je réponds à un commentaire vieux de 9 ans pour que d’autres lecteurs ne soient pas induits en erreur : si, il faut absolument que le système contienne l’arithmétique pour que le théorème de Gödel s’applique. On peut citer comme contre-exemple la théorie des corps réels clos, qu’on pourrait approximativement décrire comme étant aux nombres réels ce que l’arithmétique est aux nombres entiers. Cette théorie est complète et donc décidable, c’est le théorème de Tarski-Seidenberg. Il y a des quantités d’autres exemples.
On peut aussi penser à la logique propositionnelle, qui est beaucoup plus simple que la logique du premier ordre, tellement simple qu’elle est décidable (son problème de décision est exactement le complémentaire de QBF, et est donc PSPACE-complet).
De plus, il me semble douteux que la notion de système formel comprenne la propriété d’être décidablement axiomatisé. Je ne crois pas qu’il y ait une définition universellement acceptée en logique du terme « système formel ». En revanche, la définition d’une théorie du premier ordre est universelle, et elle n’inclut certainement pas cette hypothèse.
Sur la vidéo tu dis en ce qui concerne la démonstration du th de Godel quand l affirmation G est fausse et démontrable alors il y a incohérence ! Je ne comprends pas car on peut toujours démontrer une affirmation fausse , par exemple par le absurde ! Non?
Aviez – vous lu Godël Escher Bach de Douglas Hofstader ?
Il fait des parallèles intéressants entre le théorème de Godël, la musique de Bach et l’oeuvre d’Escher.
C’est un livre assez ardu mais magnifique et fascinant !
Pourquoi Bach ? Par la construction de sa musique parfois en canon qui fait référence à elle même.
Idem pour Escher avec des dessins s’auto référençant ou pas et plaçant le spectateur dans et/ou hors de l’oeuvre.
Il y a aussi pas mal de référence à l’informatique dans ses aspects les plus fondamentaux.
C’est bien écrit avec souvent les récits d’Achille et de la Tortue qui discourent sur la vérité ou pas de certaines idées tout en finesse !
Ce livre est un essai de vulgarisation sur le théorème de Gödel.
Douglas Hofstadter a d’ailleurs eu le prix Poulidser en son temps pour cet essai.
Oui je l’ai lu il y a quelques années, sans parvenir à le finir. Je l’ai reparcouru rapidement en écrivant ce billet, mais j’ai été un peu deçu. Je trouve qu’il plonge trop vite dans les concepts trop formels. Comme le livre est très long, je trouve qu’il aurait pu prendre son temps !
Bonjour, et merci pour cette article très intéressant (vraiment).
Je ne suis pas certain d’avoir tout bien compris dans els détails, mais j’ai à peu près compris l’idée 🙂
Par contre, en lisant ceci :
« Le premier théorème dit que tout système est soit incomplet, soit inconsistant. L’incomplétude est un problème, mais l’inconsistance est une catastrophe ! On aimerait donc pouvoir s’assurer qu’un système donné est incomplet plutôt qu’inconsistant. Ce que dit le deuxième théorème, c’est qu’on ne peut pas démontrer la consistance d’un système formel en restant à l’intérieur de celui-ci. »
je me pose la question suivante :
On veut démontrer la consistance d’un système A. Si je comprends bien, pour cela il faut travailler dans un système B. Mais dans ce cas, la démonstration qu’on essaie de faire (que le système A est consistent) peut être inconsistente, et prouver que le système A est consistent alors que ce n’est pas le cas ?
Merci pour cette belle vulgarisation du théorème de Gödel ! Je signale juste une petite ambiguité : l’ensemble des axiomes doit être récursif, et non récursivement énumérable. En effet, comme c’est dit dans l’article, « il doit exister une procédure « finie » pour décider si une proposition donnée fait partie des axiomes ou non ». Du coup c’est en fait l’ensemble des théorèmes qui sera récursivement énumérable : si un énoncé est un théorème, on finira toujours par le découvrir avec un peu de patience (en essayant toutes les preuves possibles à partir des axiomes). C’est pour les non-théorèmes qu’on est embêté !
Le théorème s’applique tout aussi bien à des systèmes semi-décidablement (= récursivement énumérablement) axiomatisés, même si c’est assez peu intéressant et rarement mentionné.
https://jean.abou-samra.fr/blog/goedel/#semidec-axiomatisee
En quoi « Tous les Crétois sont des menteurs » est il un paradoxe? Il signifie que le crétois qui le dit est un menteur, et qu’il existe donc des crétois qui disent la vérité.
Dans le langage courant un menteur est quelqu’un qui dit plus souvent que les autres – les gens « normaux » – le contraire de ce qu’il croit vai. Ce n’est donc pas quelqu’un qui dit toujours le contraire de la vérité, mais seulement quelqu’un qu’il est plus risqué de croire..
Les mathématiques utilisent les mots courants avec un sens précis, souvent tellement précis qu’avec le sens ordinaire des mots un énoncé mathématique n’a plus aucun intérêt.
A ma conaissance il n’y a pas de définition mathématique de « menteur »!
En fait ça l’est car cette phrase était énoncée par un Crétois… 🙂
« Mais on peut aussi très bien décider d’ajouter son contraire à notre liste d’axiomes. Puisque la proposition est indécidable, on ne crée pas d’inconsistance. Mais qu’est-ce qu’on obtient si on fait ça ? »
Je suis vraiment novice sur le sujet mais comme le remarque jch, autant la notion de « vrai » semble à peu près claire, autant son contraire (la « non-vérité ») exprime un truc très vague: il peut exister un crétois qui dit la vérité, ou deux ou tous. Le « non-vrai » n’est pas vraiment une catégorie utile (de même que les « non-éléphants » ne sont pas une classification très utile en biologie) Du coup j’ai du mal à imaginer qu’on arrive à grand chose en ajoutant la négation d’une proposition dans une liste d’axiome…
Ce qui est amusant, c’est que si une théorie est complète alors il n’y a qu’un seul modèle.
Ce qui fait que si je peux construire deux modèles (non équivalent) alors la théorie incomplète.
Par contre le second théorème d’incomplétude dit surtout que la cohérence de la théorie n’est pas démontrable dans son propre langage.
En math c’est assez clair, une proposition est non-vraie (fausse) si son contraire est vrai. Donc c’est bien définit ! Il n’y a donc aucun problème à ajouter le contraire d’une proposition indécidable (contraire qui se trouve bien sûr elle-même tout aussi indécidable).
Pour visualiser, le mieux est de prendre la géométrie d’Euclide (qui rappelons le ne fait pas partie des systèmes formels « couverts » par Gödel, puisqu’il ne contient pas l’arithmétique) Si on ne prend que les 4 premiers axiomes (et pas celui sur les parallèles), on obtient un système incomplet puisque l’axiome des parallèle n’y est pas démontrable, ni son contraire. On peut décider de l’ajouter, mais on peut décider d’ajouter autre chose, comme le fait qu’il y a une ou une infinité de parallèles. Mais du coup on change de modèle.
Là où je rejoins ton point, c’est que stricto sensu, il faudrait décomposer l’axiomes des parallèles de la géométrie euclidienne en 2 axiomes :
5a) Il existe au moins une parallèle à une droite donnée passant par un point extérieur à cette droite
5b) Il existe au plus une parallèle etc.
Ni 5a ni 5b ne sont démontrables. Donc on peut décider d’ajouter non-5a (qui implique 5b) et on a zéro parallèle. Mais si on ajoute non-5b, ce que je me demande, c’est si on peut construire un modèle géométrique telle qu’il existe un nombre fini (disons 42) de parallèle à une droite donnée.
Mmh, en fait il vaudrait mieux écrire 5b sous forme d’unicité. Du genre si il existe D1 et D2 tel que (…) alors D1=D2. Mais je n’ai pas le courage de réfléchir à ce que veut dire la négation d’une proposition d’unicité…
Attention quand même, cela dépend de la nature de la proposition. Les formules non prouvables peuvent être vraies, ou indépendantes. Exemple :
1/
Pour toute théorie mathématique T, on peut (facilement, si si) construire un programme P (un algorithme) tel que la théorie ne pourra pas prouver que ce programme ne termine jamais.
Bien évidemment, ce programme ne termine pas, car s’il se terminait, on pourrait faire son execution pas à pas et cela constituerait une preuve qu’il s’arrête.
Donc même si « P s’arrête » et « P ne s’arrête pas » ne sont pas prouvable dans T, si j’ajoute l’un ou l’autre comme axiome, je vais avoir des problème : si j’ajoute celui qui est vrai, tout va bien, et T est un peu plus puissante. Si je rajoute celui qui est faux, je n’ai plus de modèle pour ma théorie, on peut donc considérer qu’elle n’est plus consistante, même si je n’obtiens pas de contradiction immédiate.
C’est le même problème avec la formule « la théorie T est consistante ». Ce n’est pas prouvable dans T, mais on espère bien que c’est vrai ! et on ne va pas s’amuser à rajouter l’axiome contraire.
2/
Au contraire une formule F indépendante de T sera non prouvable dans T, et T+F ainsi que T + non F seront deux théories différentes valides comme l’exemple précédent sur les géométries qui seront euclidiennes, sphériques ou hyperboliques selon le nombre de parallèle à une droite par un point.
Tiens je ne suis pas sûr d’être d’accord !
Sur le point 1), je passe car je ne suis pas assez familier avec la formulation « algorithmique ».
Sur le point 2), je n’arrive pas à comprendre ce que « indépendant » veut dire. Pour moi, une formule F est
d’une part :
– soit démontrable,
– soit réfutable,
– soit indécidable,
et ce caractère est relatif à la théorie T (c’est à dire au système axiomatique) considéré;
d’autre part :
– soit vraie
– soit fausse
et ce caractère est relatif au modèle M considéré.
Sachant qu’on peut très bien faire des maths en ne considérant qu’un système axiomatique T sans aucune référence à un modèle et ne jamais parler ni de « vrai » ni de « faux ». Juste de ce qui est démontrable/réfutable et de ce qui ne l’est pas.
Donc pour moi, si on prend pour T les axiomes d’Euclide SANS le 5ème axiome (celui des parallèles), alors on a une proposition indécidable qui est le nombre de parallèles passant par un point donné. On peut choisir d’ajouter à T l’une des 3 versions du 5ème axiome : « une parallèle », « aucune parallèle », « une infinité de parallèles »
Maintenant si dans le même temps on a choisi de considérer comme modèle « la géométrie dans le plan », alors parmi les 3 versions du 5ème axiome, il n’y en a qu’une qui est compatible avec M (« vraie ») et deux qui ne le sont pas. Donc si on fabrique T’ en ajoutant à T « aucune » ou « une infinité », alors T’ n’axiomatise plus M, mais un modèle M’ qui est Riemann ou Lobachevsky.
Ben je pense qu’on est d’accord. En tout cas ton explication me semble juste et compatible avec ce que j’ai dit avant.
Une proposition indépendante veut simplement dire qu’on peut étendre le modèle dans lequel on travaille par deux modèles différents, l’un ou la proposition est vraie et l’autre ou elle est fausse. Dans ce cas là, la proposition est forcément non prouvable.
Alors qu’une proposition peut être considérée comme vraie s’il n’existe pas de modèle dans laquelle elle est fausse. Dans ce cas là, on peut avoir une preuve de la proposition ou pas !
Sinon, je ne vois pas trop l’intérêt de faire des maths dans une théorie sans modèle. D’ailleurs en général, on fait toujours des maths dans un modèle, sans vraiment considérer la théorie qui est derrière. C’est le cas d’a peu près tous les maths classiques jusqu’en licence inclue (et même après). L’intérêt des maths est en général de comprendre les relations entre des objets d’un certain univers, on considère donc en général un univers avant une théorie.
Les seuls cas où on s’intéresse un peu à la théorie, c’est quand on utilise l’axiome du choix, mais en général, ça se transforme en voyage dans la quatrième dimension avec Zorn et compagnie. Et bien sur, quand on fait de la théorie des ensembles ou de la logique, on s’intéresse à ces questions.
Tous ces problèmes de non prouvabilité sont liés à des problèmes en physique. Le problème classique en mécanique est le problème à 3 corps. Tu considère un système à 3 corps liés par la gravitation et tu te demandes « est-ce qu’il va y avoir une collision ? ». La réponse est indécidable. Bien sur, dans des cas simples, juste avant une collision, on pourra répondre « oui », ou « non pas d’ici 1 an ». Mais si on cherche une réponse absolue, on ne peut pas toujours la donner. Pourtant soit il va y avoir une collision soit non, c’est donc une proposition non prouvable (ou non calculable), mais vraie ou fausse.
Au contraire, on peut faire des modèles d’univers bizarres (par exemple des multivers) tout à fait non prouvables qui peuvent être vrais (univers parallèles indépendants) ou faux (un seul univers). Mais s’il n’existe rien pour vérifier dans quel modèle on est, cela devient plus de la métaphysique.
J’espère avoir été plus clair !
En fait si une théorie est cohérente, il existe toujours un modèle de cette théorie ! (théorème de complétude de Gödel. Donc être indécidable est exactement équivalent à être vrai dans un modèle de la théorie et faux dans un autre.
@DK non, justement, je viens d’essayer d’expliquer que ce n’est pas équivalent, et qu’une proposition peut-être improuvable et vraie dans tous les modèles de cette théorie. Bon au temps pour moi pour ma pédagogie…
@Xoff : non j’avais bien compris ce que tu voulais dire, mais je pense que tu trompes.
En fait Gödel a aussi montré le théorème de complétude : si un énoncé est vrai dans tout modèle d’une théorie T, alors il est prouvable dans T.
cf cette page pour plus de renseignements : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_compl%C3%A9tude_de_G%C3%B6del
Hi hi, non ça n’a rien à voir. Il s’agit là des prédicat du premier ordre ! mais c’est beaucoup plus simple qu’une théorie mathématique classique. On ne peut pas faire de fonctions arithmétiques avec les prédicats du premier ordre et donc l’incomplétude ne s’applique pas à ce cas là. On ne parle donc pas de la même chose ici.
En gros, on a besoin de la multiplication et de la composition de fonction pour que les problèmes d’incomplétude apparaissent.
@Xoff: Le système de déduction utilisé est bien le calcul des prédicats, mais ça marche pour tout jeu d’axiomes ! Il ne faut pas confondre axiomes et règles de déduction. On peut par exemple prendre les axiomes de Peano (PA), qui sont suffisants pour le théorème d’incomplétude. La page wikipedia en anglais aide peut-être à y voir plus clair : http://en.wikipedia.org/wiki/G%C3%B6del's_completeness_theorem
En particulier la phrase suivante: « Precisely, we can systematically define a model of any consistent effective first-order theory T in PA ».
Tu peux prendre n’importe quel système d’axiomes et te limiter à la logique du premier ordre et tout est décidable. Mais la plupart des formules intéressantes seront des formules de logique d’ordre supérieur !
D’où l’indécidabilité qui apparait. Mais oui, c’est vrai, si tu te limites à la logique du premier ordre, vrai = décidable. Mais tes formules ne décriront pas grand chose d’intéressant au niveau des structures de tes modèles. En particulier tu ne pourras pas faire de formules sur des propriétés véritablement arithmétiques dans le sens d’un calcul algorithmique.
Le théorème d’incomplétude concerne également la logique du premier ordre. Et on peut déjà dire des trucs très intéressants au premier ordre, comme la conjecture de Goldbach (tout entier pair à partir de 4 est la somme de deux premiers), ou la conjecture des nombres premiers jumeaux (il existe une infinité de nombres premiers jumeaux, c’est-à dire x et x+2 premiers).
Tu ne peux pas me dire d’abord que le théorème de complétude s’applique à tout pour ensuite me dire que le théorème d’incomplétude s’applique à tout 🙂 Il faut que tu choisisses (bien !)
En ce qui concerne la logique du premier ordre, le fait que la complétude existe ne veut pas dire que pour certaines formules on ait forcément déjà trouvé la preuve. Il y a une différence entre « une preuve existe » et « j’ai trouvé la preuve ». Donc oui, il y a des formules de premier ordre intéressantes.
Comme le dit la page wikipédia que j’ai posté plus tôt : » The name for the incompleteness theorem refers to another meaning of complete ».
Le théorème de complétude parle du système de déduction (ici le calcul des prédicats du premier ordre). Il affirme que si un énoncé est vrai dans tout modèle qui satisfait un ensemble d’axiomes A, alors on peut déduire cet énoncé depuis A, avec le calcul des prédicats. Par contre, il peut très bien rester des énoncés indépendants de cet ensemble d’axiomes.
Le théorème d’incomplétude dit justement que de tels énoncés existent, pour tout ensemble d’axiomes récursif contenant PA.
Donc ces deux théorèmes ne sont pas incompatibles et peuvent s’appliquer à une même théorie, malgré ce que leurs noms laissent entendre.
Je suis d’accord avec toi, mais je crois comprendre ce que tu n’as pas compris. Les énoncés du type Goldbach ne peuvent pas être indépendant : s’il est faux, il existe un contre-exemple qui sera un entier présent dans tous les modèles. Donc tu vois bien que ce type de proposition est soit prouvable soit vrai.
Pour avoir une proposition indépendante, il faut s’intéresser forcément à des propriétés plus complexes.
Indépendante ne veut pas dire non prouvable.
Dans le cas de Goldbach, effectivement il ne peut pas être faux (dans N !) et indépendant. Par contre il peut très bien être vrai dans N et indépendant. Cela tient au fait que c’est une formule très simple du type pour tout x blabla (où blabla ne dépend que de quelque chose de fini). On dit que la formule est de complexité Pi_1. Mais Goldbach pourrait très bien être un exemple de propriété indécidable, auquel cas elle serait forcément vraie dans N (et fausse dans un autre modèle).
Pour les nombres premier jumeaux par exemple ça se complique, car c’est une formule Pi_2, plus complexe, du type « pour tout x, il existe y, blabla ». (pour tout x, il existe y>x, tels que y et y+2 sont premiers). Du coup, même si c’est toujours une formule du premier ordre, elle peut être vraie et indépendante, ou fausse et indépendante.
Bien sûr peut-être que ces deux formules sont démontrables et qu’on a juste pas trouvé la preuve, mais elle peuvent également être indémontrables.
Ah ben vous êtes chauds tous les deux !
Pour ma part, je crois avoir compris d’où vient mon erreur. Je pensais qu’un modèle associait nécessairement la valeur « vrai » ou « faux » à toute formule (syntaxiquement correcte) du langage choisit. Je ne pensais pas qu’un modèle pouvait être muet sur certaines formules. Mais il semble que si !
Non David tu avais bien raison, un modèle associe effectivement « vrai » ou « faux » à toute formule bien construite.
En fait pour moi, indépendant ça veut dire ni vrai ni faux ou plus raisonnablement vrai si on étends la théorie d’une certaine manière et faux si on le fait d’une autre manière.
Quand tu me dis « vrai dans N et indépendant » je ne comprends pas ce que tu veux dire.
@David oui, je crois que tu as compris ! Un modèle n’est qu’une collection d’objets « qui existent » et vérifient toute la théorie.
Tu peux relire le commentaire de ScienceEtonnnante plus tot, qui était très bien.
« démontrable et indécidable » sont des propriétés de la théorie.
« vrai et faux » sont des propriétés du modèle.
Il se trouve que si ton système de déduction est raisonnable, tu as
démontrable => vrai dans tout modèle
et si en plus ton système de déduction est complet (c’est le cas pour le calcul des prédicats utilisé habituellement), la réciproque est également vraie : vrai dans tout modèle=>démontrable.
Ce que j’entends par « vrai dans N et indémontrable » devrait être plus clair maintenant : dans N il n’y a pas de contre-exemple à la conjecture, mais il y en a dans des modèles « non-standards », qui comportent d’autres nombres entiers bizarres, et vérifient quand même les axiomes de Peano.
cette discussion devient marrante 🙂 mais je dois aller me coucher. Enfin pour moi un modèle n’est qu’une structure qui vérifie la théorie. Allez bonne nuit à tous.
Christophe, tu es un vrai physicien !
Voici ce que je crois avoir compris. Tout part d’un langage qui est un ensemble fini de symbole, à partir duquel on peut construire des chaînes finies de symboles (les formules), et des règles qui nous disent quels sont les formules syntaxiquement valides.
Bon, ensuite je crois comprendre qu’un modèle, c’est en gros « une application » qui à toute formule syntaxiquement correcte associe la valeur « vrai » ou « faux ». Il y a certainement des contraintes à poser comme une sorte de « fermeture » ou « consistance » sous application des règles de la logique. Donc pour moi dans un modèle donné, toute formule correcte est soit vraie, soit fausse.
Si je te comprends bien Christophe, il y aurait une troisième possibilité qui est que le modèle ne dit rien sur certaines formules (que tu qualifies alors d’indépendantes). Dans une vision « à la physicienne », ça me va très bien comme situation (c’est à dire qu’un modèle est une représentation « réelle » ou « physique » d’un truc qui « existe »…- je mets des guillemets). Mais dans ma vision « formelle » (tout physicien que je sois) je pensais qu’un modèle se devait de se prononcer sur la véracité de toutes les formules du langages.
En l’espèce, il me semble que l’arithmétique dans N associe bien une valeur vrai ou faux à toute formule bien construite à partir des symboles usuels. Me trompe-je ? Se pourrait-il qu’il existe des formules arithmétiques indépendantes ?
Pour les axiomes, la situation est claire : on peut toujours ajouter un axiome qui est une formule indécidable, ou bien ajouter son contraire. Mais du coup on axiomatise plus l’arithmétique dans N, on axiomatise un autre modèle d’arithmétique non-standard.
Satané Gödel, je crois que je n’en comprendrai jamais vraiment tous les recoins !
Bon je vais me coucher aussi 🙂
Un modèle est juste une structure mathématique qui vérifie la théorie. Dans un modèle donné, chaque formule est vraie ou fausse, pas de troisième choix. Par exemple soit il existe une infinité de nombres premiers jumeaux dans N, soit non. Le problème c’est que la théorie décrit plusieurs modèles différents. C’est pour ça que certains énoncé sont indécidables : ils sont vrais dans certains modèles de la théorie et faux dans d’autres. Le théorème de Gödel dit que toute théorie parlant de l’arithmétique aura plusieurs modèles différents.
Après une bonne nuit de sommeil et en relisant nos postes, je suis d’accord avec DK. J’ai même raconté des âneries sur la logique du premier ordre parce que j’ai écrit trop vite et pensé au calcul sans quantificateurs !
Pour les modèles aussi, je suis d’accord, mais je réalise que j’ai une vue platonicienne des mathématiques. D’un point de vue métaphysique, je considère qu’un modèle existe ou pas. Cela n’empêche pas des modèles apparemment contradictoire d’exister en même temps, si on peut les mettre dans un modèle plus global (un peu comme différentes formes de géométries peuvent être considérées comme des cas particuliers dans une dimension supérieure si vous voyez ce que je veux dire).
Du coup je réalise que je n’ai rien compris à cette histoire de modèle non standard des entiers, car si on se limite aux « entiers finis » (un nombre fini de +1 après 0), tous les modèles représentent les mêmes entiers et je ne vois pas comment on peut être indépendant. Je vais aller voir un collègue logicien je pense.
La nuit porte conseil 😉
Pour les entiers non standards, ce sont justement des entiers qui ne s’écrivent pas SSSS…SSS0. En fait même si c’est ce qu’on entend par « entier », aucun des axiomes de Peano ne force les entiers à être de cette forme, et c’est impossible de trouver des axiomes qui expriment ca.
Par exemple un modèle non standard de Peano peut ajouter aux entiers standards les entiers « non-standards » consistant en couples (x,y) où x est rationnel et y entier relatif. On peut définir l’addition et la multiplication sur cet ensemble bizarre, de manière a respecter les axiomes de Peano. Mais (2/3, -8) n’est pas de la forme SSS…SSS0.
ta soeur
Pingback: A_classer | Pearltrees
Merci pour cette belle vulgarisation du théorème de Gödel ! Je signale juste une petite ambiguïté : l’ensemble des axiomes doit être récursif, et non récursivement énumérable. En effet, comme c’est dit dans l’article, « il doit exister une procédure « finie » pour décider si une proposition donnée fait partie des axiomes ou non ». Du coup c’est en fait l’ensemble des théorèmes qui sera récursivement énumérable : si un énoncé est un théorème, on finira toujours par le découvrir avec un peu de patience (en essayant toutes les preuves possibles à partir des axiomes). C’est pour les non-théorèmes qu’on est embêté !
Ah, merci de la correction !
Pingback: Le théorème d’incomplétude de Gödel | C@fé des Sciences | Scoop.it
Il aurait été prétentieux de la part des mathématiciens de penser qu’ils peuvent construire un système parfait.
Les maths sont un langage, une construction, une interprétation, un description, bref tout ce qu’on veut sauf la réalité. Le « vrai » n »étant par ailleurs qu’une question de point de vue.
Je me suis toujours demandé également dans quelle mesure on pouvait décrire une réalité, ou ce qu’on en perçoit, quand on en fait partie.
Il parait donc évident (mais pas forcément facilement démontrable) que quoiqu’on fasse on rencontre des limites infranchissables.
Tiens ce commentaire montre que je n’ai pas bien fait mon travail ! 🙂
Un des problèmes du théorème de Gödel est justement sa sur-interprétation dans un cadre plus large que celui qui est le sien. Je pensais avoir assez insisté là-dessus.
On entend parfois des réactions du genre « Ah les mathématiciens enfermés dans leur tour qui s’imaginent que tout est démontrable wouarf wouarf wouarf ! Et ils avaient besoin d’un théorème pour leur dire que non… » Or que ce soit clair à nouveau, le théorème de Gödel s’applique dans un cadre très restreint et très précis qui est celui des systèmes axiomatiques. Il n’y a aucune prétention à se demander si l’arithmétique est axiomatisable par un système complet.
Les matheux n’ont pas besoin de Gödel pour savoir que la proposition « Le Requiem de Mozart est-il beau ? » est indécidable…
D’ailleurs il existe des systèmes complets (comme l’arithmétique de Presburger, qui modélise les nombres entiers avec l’addition), ce qui démonte un peu les argumentations du type « Il aurait été prétentieux de la part des mathématiciens de penser qu’ils peuvent construire un système parfait. »
Gödel se sent de plus en plus autrichien et surtout viennois : il aime la ville, son atmosphère intellectuelle et sa vie universitaire. Il demande, à la fin de l’été 1928, la nationalité autrichienne et n’est officiellement plus tchèque le 26 février 1929, trois jours après la mort de son père. Malgré son deuil, Gödel termine sa thèse de doctorat Sur la complétude du calcul logique qu’il présente le 6 juillet 1929 à son directeur de thèse Hans Hahn et à un de ses rapporteurs, Philipp Furtwängler. Dans ce mémoire dactylographié de 30 pages, le jeune mathématicien, âgé de 23 ans, expose divers résultats très importants de logique que nous allons détailler dans ce chapitre. Il démontre la complétude sémantique de la logique des prédicats du premier ordre, ce qui est satisfaisant pour l’esprit, et en déduit que tout système d’axiomes du premier ordre non contradictoire possède un modèle : il existe un ensemble d’objets qui vérifient les axiomes du système. Construire un modèle, c’est « ajouter de la chair autour des os » d’un système axiomatique, et ainsi établir qu’il est cohérent, c’est-à-dire non contradictoire.
wouaouw.. merci à Judith.D Ware, merci à cet illustre physicien, chercheur ,mais » ajouter de la chair autour des os » d un système axiomatique, établir qu il fut cohérent,non contradictoire,par un Mental sélectionné,ne signifie t il pas que cela nous dirige inévitablement vers La Source Centre Première?à vous Tous et toutes les Matheux « physiciens de la Matière », chercheurs de qualité et de savoir, le système, la recherche ne sera complète que lorsque la Conscience se marie avec la Science, pour une réunification Harmonieuse de tous
vos concepts établis, vos circuits mentaux élevés vers des Principes Spirituels conjugués.. »Science sans conscience n est que ruine de L ame » de l homosapiens vers L homospiritus pour chacun , libre arbitre vers une Nouvelle Conscience Planéterre, actuellement dans l espace/temps 2013 sur Urantia( Notre Planète)!
Lire La Particule de Dieu- l ultimaton- l infinitron-le métatron-les muons- les huons-ect-Energie divine de la Créature vers le Créateur..Urantia BOOK- Brodcasturantia.com- destiné à toute l Humanité .CHERCHEURS DE L eSPRIT ! à bon lecteur Salut!
Bernadette de France!
Jacques Bouveresse dans « Prodiges et vertiges de l’analogie » s’est battu contre ceux qui disent n’importe quoi sur le théorème d’incomplétude, et notamment contre Regis Debray. Sur la vie de Gödel il y a le livre de Yannick Grannec « La Déesse des petites victoires », qui donne un bon aperçu de la « folie » de Gödel, de ses tourments intimes et de ses très bonnes relations avec Einstein.
Y a t-il un moyen de mesurer l’incomplétude, c’est à dire de savoir combien de fenêtres sont inateignables : 2 %, 50 % ?
Il faut lire le livre de Palle Yourgrau (Einstein/Gödel) qui explique notamment que pour Gödel le fait que l’on puisse trouver des solutions aux équations d’Einstein avec des courbes temps de genre fermé (univers de Gödel) démontre que la théorie de la Relativité Générale tombe sous le coup des théorèmes d’incomplétude. Selon lui, le temps de la RG n’est que le cour du temps. L’incomplétude en serait la flèche… C’est une idée que l’on ne souligne jamais quand on expose l’univers de Gödel.
En ce qui me concerne, je trouve toujours très spécieux d’insister sur la folie de Gödel… C’est souvent pour marginaliser ces résultats…
Pour ma part, j’énoncerais le théorème de Gödel ainsi :
« Toute théorie capable de formaliser l’arithmétique, si elle est récursivement axiomatisable, ne peut-être complète et consistante à la fois. La consistance d’une telle théorie est intrinsèquement indécidable »
Le second alinéa du théorème (que l’on nomme parfois second théorème d’incomplétude) dit que compléter trivialement les axiomes ne sert à rien : l’ensemble axiomatique peut-être fini ou infini dénombrable, le théorème de Gödel s’applique…
N’en déplaise à Jacques Bouveresse, une théorie qui se dispense de formaliser la structure logique de l’arithmétique (même dans le cadre des sciences humaines…) ou qui ne serait par récursivement axiomatisable n’est plus une théorie… C’est ainsi que par exemple, pour Gôdel, la relativité restreinte, n’accède pas au rang de théorie…
Les résultats de Gödel ne sont pas la propriété d’une élite (Sokhal et Bouveresse en font-ils partie ?). Il est plus aisé aujourd’hui pour un jeune lycéen qui baigne depuis toujours dans le monde de l’informatique de comprendre Godel ou le problème de l’arrêt de Turing…
Bouveresse reste peut-être aussi attaché au positivisme logique car finalement il n’a pas compris les résultats de Gödel…
J’ai trouvé que c’était de la très belle vulgarisation, mais quand même « les propositions indécidables sont tellement tordues qu’on ne les croise pour ainsi dire jamais » me semblent être assez déconnecté du sujet. Ne serait-ce que mentionner la possibilité de l’indécidabilité de P = NP me semble être complétement pertinent.
Excellente vulgarisation de ces idées, très claire, bravo.
A corriger : « si est seulement si » est/et, plusieurs fois.
Bien vu, je suis impardonnable ! Je corrige ça vite….
Philosophiquement, le théorème d’incomplétude signifie que la science mathématique ne peut pas se suffire à elle-même, qu’elle doit partir d’axiomes, d’hypothèses, de faits ou de lemmes non démontrables.
Ce qui par extension signifie que la raison pure ne peut conduire à la connaissance complète.
Lorsque le Christ dit à Pilate : « Je suis né et je suis venu dans le monde pour rendre témoignage à la vérité. Quiconque est de la vérité écoute ma voix » ; il ne dit pas « les mathématiques, la logique et la raison pure vous instruiront de la Vérité. »
Enfin, Pilate lui répond : « Qu’est-ce que la Vérité ? », qui est la base du relativisme. Ce relativisme n’est pas scientifique puisque la Science (dure en tous cas) postule qu’il n’y a qu’une vérité scientifique, et qu’elle est logique (ce qui est un axiome ou une croyance d’ailleurs).
Bien qu’ayant le plus grand intérêt pour la Science, je trouve personnellement que plus la Science avance, plus elle dévoile une complexité sans fin et de moins en moins déterministe (cf. la mécanique quantique), et qu’elle tend à faire penser qu’il y a bien d’autres réalités que le monde sensible et purement matériel.
Désolé mais il y a confusion dans cette phrase: « Philosophiquement, le théorème d’incomplétude signifie que la science mathématique ne peut pas se suffire à elle-même, qu’elle doit partir d’axiomes, d’hypothèses, de faits ou de lemmes non démontrables. »
Ce n’est pas du tout ce que dit le théorème (il faut relire l’article plus en détail!). Au contraire, c’est même le point de départ du théorème et non sa conclusion, et tout le monde acceptait avant ce théorème, et accepte toujours, que les maths fonctionnent à partir d’axiomes et pas à partir de rien. Au passage, « lemme non démontrable » est un contresens parfait, puisqu’un lemme est quelque chose de démontré à partir des axiomes.
De manière générale, la seule chose qui manque à cet excellent article est une mise en garde contre les dérives philosophico-sociologico-economico-délirantes que ce théorème a inspiré à de trop nombreuses personnes. Le théorème de Gödel est un beau théorème, mais il parle de systèmes axiomatiques en mathématiques formelles et de rien d’autre. Il a des hypothèses très précises (qui ne sont pas toujours vérifiées: certains systèmes axiomatiques SONT complets comme l’arithmétique de Presburger), et n’a strictement aucune conséquence sur la religion, le libéralisme, ou quoi que ce soit en dehors des maths. On peut au mieux dire « tel phénomène rappelle un peu le théorème de Gödel », mais c’est surtout dangereux, car trop de gens qui ne le comprennent pas essaieront de s’en emparer pour soutenir une idéologie ou un parti-pris philosophique.
Je ne suis d’accord ni avec le commentaire ni avec la réponse de Denis. On a droit toujours au même débat : il serait temps de le dépasser 83 ans après l’énoncé des 2 théorèmes d’incomplétude car le temps et les idées ne ce sont pas arrêtées en 1931…
Franz, la vérité de Gödel c’est la vérité absolue, elle n’a rien de « relative » justement… Ce n’est pas la « vérité de Carnap », c’est à dire la vérité limitée aux propositions démontrables. En effet, si Gödel affirme que le vrai excède le démontrable (ou pour les mathématiciens le récursivement dénombrable), il démontre en fait que ce « vrai indécidable » existe bien (on parle quelque fois de vrai « justifié » pour dire que l’existence de ce vrai est démontrée mais que son contenu ne peut-être trivialement explicité) en construisant la proposition métamathématique :
– »
« le vrai excède le récursivement dénombrable (démontrable) »
est une proposition récursivement dénombrable (démontrable)
« .
Ainsi Carnap se trompe avec son « vrai conventionnel » et même Gödel peine à donner du « contenu » a cette objet (fait) mathématique qu’est l’incomplétude avec sa « théorie des concepts » avortée.
Denis c’est injuste de dire que les conséquences de ces théorèmes n’impactent que les mathématiques – et encore « formelles ». Les mathématiques autres que formelles pour moi c’est de la numérologie et celà relève de l’esprit magique Ensuite, si Gödel (qui suit ainsi Hilbert and cie) retient un système axiomatique récursivement dénombrable capable de formaliser l’arithmétique des entiers naturels et non pas des arithmétiques « complètes » du type Presburger c’est qu’une logique de premier ordre n’est pas assez puissante. On peut répondre aux problèmes de décision posées par le jeu « la chasse au Wumpus » avec un système logique du premier ordre mais pas à celle des fondements des mathématiques (Grundlagen der Mathematik).
L’incomplétude de Gödel (son caractère obstructif) vient justement du fait qu’une logique du premier ordre n’est pas assez puissante et que la logique du second ordre est elle trop puissante : en théorie de la calculabilité on parle de « saut de Turing ».
En second lieu, aujourd’hui, beaucoup de mathématiciens (comme Alain Connes par exemple) pensent que ces « obstructions » mathématiques compromettent l’élaboration d’une théorie physique du tout (une théorie quantique englobant la gravité comme la relativité d’Einstein) et qu’il faut intégrer ces obstructions dans le « modèle » conceptuel qui en dernière analyse est un modèle mathématique. Il n’y aurait pas ainsi de changement de paradigme entre le fait mathématique et le fait physique.
Enfin, on peut faire de la théologie avec Gödel (je sais qu’en France aujourd’hui on est plus dans une époque d’interdiction que de liberté mais bon ce ne sont pas les mathématiciens qui tiennent le monde…).
Par exemple transposer le débat trinitaire sur le plan de la logique formelle :
– le père = le vrai absolu / le fils = le vrai décidable / le Saint-Esprit = le vrai justifiable »
dans son domaine Gödel est un hérétique acacien homoïousien en rupture avec les Nicéens strictes (c’est à peu près la position orthodoxe de l’Eglise catholique aujourd’hui….).
Comme disait Einstein « Dites moi ce que vous entendez par Dieu et je vous dirai si j’y crois »…
Sinon je suis d’accord avec toi Denis sur le fait qu’il ne faut pas dire n’importe quoi sur Göde et ses théorèmes logiques.
Merci pour ta réponse intéressante Axel, j’y réponds à mon tour 🙂
Effectivement j’ai mis « formelles » pour enfoncer le clou, et parce que Gödel utilise leur côté le plus formel qui n’apparaît pas dans l’utilisation courante, mais qui est toujours sous-jaçent.
« L’incomplétude de Gödel (son caractère obstructif) vient justement du fait qu’une logique du premier ordre n’est pas assez puissante et que la logique du second ordre est elle trop puissante : en théorie de la calculabilité on parle de « saut de Turing ». »
Je ne suis pas sûr de ce que tu veux dire avec cette phrase. L’obstruction est déjà atteinte au premier ordre dans les systèmes dont Gödel s’occupe ici, et son théorème concerne uniquement les systèmes du premier ordre. Le problème du second ordre n’est pas qu’il est « trop puissant », mais plutot qu’on ne peut pas lui donner une sémantique univoque, comme le montre Gödel avec son (moins fameux mais tout aussi joli) théorème de complétude (du calcul des prédicats du premier ordre). Dès lors, il devient difficile de répondre à la question de la complétude ou non d’un système du second ordre, car on ne sait pas très bien ce qu’on veut dire par là. D’ailleurs le lien avec le saut de Turing existe, mais ce n’est pas « on parle de saut de Turing » pour passage au second ordre, c’est plus subtil que ça. De plus la calculabilité est un domaine bien spécifique, et le second ordre est beaucoup plus large que ce que si passe dans ce domaine
.
Je maintiens que ce théorème ne s’applique qu’aux mathématiques. Le piège est que les mathématiques, elles, s’appliquent à autre chose, et il appartient à chacun d’estimer dans quelle mesure elles sont valides dans le réel, et quel est leur champ d’application. L’histoire montre qu’elles sont extrêmement adaptées pour la physique, beaucoup moins pour la théologie. Dans tous les cas, les conséquences possibles du théorème de Gödel dans ces domaines dépend du pouvoir qu’on prête aux mathématiques dans leur application, qui à mon avis n’est jamais absolu. Il y aura toujours des aspects des mathématiques (et le théorème de Gödel, par son abstraction extrême, me parait un excellent candidat) qui ne s’appliqueront pas au monde réel. Je pense que le discours actuellement à la mode qui prétend que les mathématiques et la physique sont une seule et même chose se trompe profondément.
Pour ce qui est de transposer des concepts élaborés de la logique formelle pour tirer des conclusions sur des problèmes philosophiques telles que la religion, uniquemenr par analogie, chacun est libre de faire ce qu’il veut, mais à mon humble avis la valeur de tout ceci est proche de zéro (même si Gödel fut lui aussi un adepte de ce genre de petit jeu), par exemple le débat trinitaire que tu mentionnes entre à mon avis dans cette catégorie. Je suis complètement pour que la religion devienne plus logique (cf débat avec les créationnistes), mais autant ne pas le faire n’importe comment, en manipulant des concepts que les protagonistes ne comprennent pas, et en plaquant les conclusions directement des mathématiques dans le nouveau domaine.
Mes positions sur les rapports des mathématiques avec la physique ou la théologie n’engagent que moi, mais le moins qu’on puisse dire, c’est qu’il n’y a pas consensus sur ces questions, et que les mathématiques ont montré à de nombreuses reprises que certaines de leur conclusions seront difficilement applicables dans le monde réel (au hasard http://fr.wikipedia.org/wiki/Paradoxe_de_Banach-Tarski). J’ai donc une nette tendance à me méfier hautement des discours du type « le théorème de Gödel prouve que [insérer ici un énoncé qui parle de la vie réelle] ». Bizarrement personne ne s’est excité sur Banach-Tarski pour mettre fin à la famine en duplicant la nourriture… Sans doute parce que voir l’inadéquation de ces questions mathématiques sur le monde physique est beaucoup plus évident.
Denis, je comprend que l’évocation de la notion de saut de Turing te choc : le raccourci était un peu osé de ma part (d’autant que dans mon esprit je visais plus la notion de RE Turing degree). Ce que je voulais dire c’est que l’on se trouve confronté à une logique booléenne binaire avec les ordres logiques :
– soit c’est la logique d’ordre 1 et sa complétude (Gödel 1929) mais elle est insuffisante de l’épistémologie à l’ontologie car elle ne peut servir comme un métalangage car les quantificateurs ne peuvent porter que sur les propriétés dans le domaine d’interprétation du système logique (c’est ainsi que Gôdel parle de pré-théorie)
– soit c’est la logique d’ordre supérieur (2 et plus), qui peut servir comme métalangage (comme par exemple « »2+2=4″ est une proposition vrai » ou « »le vrai excède le démontrable » est une proposition vrai ») car les quantificateurs peuvent également porter sur les relations entre les propriétés dans le domaine de l’interprétation, mais qui incomplète (c’est à dire qu’elle ne peut être totalement consistante et décidable – Gödel 1930 et 1931).
Je suis d’accord avec toi pour dire que l’incomplétude existe aussi pour le premeir ordre car effectivement une logique de cet ordre ne permet pas l’établissement d’un métalangage car… elle n’est pas assez puissante pour celà… Dans ce sens, l’incomplétude de 1930-1931 doit être vue positivement car il est démontré que la logique formelle pouvait servir comme métalangage (trivialement au moins : les 2 théorèmes d’incomplétude…) mais… pas complètement.
Cantor évoquait la puissance du continu : la c’est la puissance du dénombrable ce qui est exactement la même chose en dernière analyse.
Je persiste a penser qu’il existe une similitude entre ce que Pierre Cartier nommait « groupe de galois cosmique » et l’incomplétude. Pour le reste je suis entièrement d’accord avec toi Denis et l’exemple de l’utilisation fait de Gôdel par Régis Debray suffit a le démontrer… Cependant, il ne faut pas réserver Gôdel a une élite et en discuter même si des contre sens peuvent apparaître alors (et personne n’est à l’abris même les pas les mathématiciens…).
Axel, sur les aspects mathématiques de ton commentaire il y a de grosses confusions je pense. Les deux théorèmes de Gödel, complétude et incomplétude, parlent tous les deux des systèmes du premier ordre. Je suis d’accord que les noms appellent à confusion, car ils ne parlent en réalité pas de la même partie des systèmes:
-la Complétude fait référence au système de déduction, appelé « calcul des prédicats classiques du premier ordre ». Le fait qu’il soit complet signifie qu’une fois les axiomes fixés, toutes les conséquences de ces axiomes pourront être prouvées via notre système de déduction (qui est plus puissant que la logique intuitionniste par exemple). Il est important de préciser ce qu’on entend par « conséquence »: B est conséquence de A si on ne peut pas construire un modèle (par exemple les nombres entiers, ou n’importe quelle autre structure mathématique) où A est vrai et B est faux. Notons au passage que la notion de « vrai » dans les travaux de Gödel est toujours relative à un modèle, et que la propriété G qu’il construit est vraie dans le modèle des nombres entiers et fausse dans un autre modèle M, puisque l’on sait que G est indémontrable et que par le théorème de complétude, un tel modèle M doit exister. Quand on dit indémontrable et « vrai », on sous-entend « vrai dans le modèle des nombres entiers », et cela n’a aucune valeur d’absolu.
-l’Incomplétude parle des mêmes systèmes logiques du premier ordre, mais fait cette fois référence au choix des axiomes. La force de Gödel est justement d’avoir réussi à créer un métalangage au premier ordre, en encodant les démonstrations comme de simples nombres. Dès lors, dire « il existe un nombre x tel que blabla » revenait à dire « il existe une démonstration de telle propriété ». Si on contient l’arithmétique de Peano, il est impossible de choisir assez d’axiomes pour que tout ce qu’on puisse exprimer soit démontrable. Cela signifie qu’il est impossible d’utiliser les axiomes pour spécifier complètement de quel modèle on veut parler (en l’occurrence les nombres entiers), il y aura toujours d’autres modèles avec des propriétés différentes qui seront compatibles avec nos axiomes. Les énoncés qui diffèrent d’un modèle à l’autre (comme G) seront donc indémontrables, puisque ni complètement vrais ni complètement faux dans les modèles fixés par les axiomes.
Comme tu vois, rien à voir avec le second ordre, et tout ceci prouve bien qu’il est assez difficile de savoir de quoi on parle quand on prétend appliquer Gödel. Je suis complètement pour une vulgarisation de ce théorème (ce n’est pas le cas de certains de mes collègues), qui reste très important pour les mathématiques et même l’informatique, mais cela doit toujours être fait avec beaucoup de prudence, en mettant en garde contre les analogies qui tendent les bras quand on essaie de simplifier le résultat en utilisant le langage courant. Le théorème de complétude est à mon sens tout aussi étonnant, et je suis presque surpris qu’il soit moins récupéré en philosophie car sa portée est énorme: on a trouvé un système de déduction logique qui est complet, auquel il n’y a plus rien à ajouter !
Le fait que la notion de vrai soit relative au modèle est d’ailleurs présente dans le « pour aller plus loin » de l’article.
Non, je ne fais aucune grosse confusion : je sais parfaitement que le calcul des prédicats du premier ordre n’est que semi-décidable. Sauf si on envisage un système monadique mais ce n’est plus de la logique formelle… Quand je parle de systême d’ordre supérieur, je ne vise pas unique les système d’ordre 2 et plus. Je me suis mal exprimé (c’est le pb des discussions sur internet). Le problème est le suivant : on ne peut « transformer » un système semi-décidable en un système complètement décidable et consistant sans que ce système ne puisse formaliser l’arithmétique au sens de Gödel. Moins ce n’est pas assez et plus non-plus (car alors on passe a des sytèmes à oracle dont l’oracle n’est plus dans le domaine d’interprétation de la théorie…).
« ce n’est pas le cas de certains de mes collègues » : ils peuvent toujours s’en offusquer après tout et considérer qu’ils sont le « peuple élu »…. Vive la démocratie !
Bon j’ai l’impression que c’est un peu un dialogue de sourds. Comment peux-tu dire que tu ne fais aucune confusion quand tu prétends (je te cite) que la complétude (Gödel 1929) s’applique à la logique d’ordre 1, et l’incomplétude à la logique d’ordre supérieur qui peut servir comme métalangage (Gödel 1930 et 31). Alors que justement, ces deux théorèmes s’appliquent à la même logique du premier ordre, et toute la preuve du théorème est d’exprimer des meta-propositions au premier ordre.
J’ai du mal à comprendre ton nouveau commentaire, qu’est-ce que tu entends par « transformer »?
et aussi « Quand je parle de systême d’ordre supérieur, je ne vise pas unique les système d’ordre 2 et plus. » –> quoi d’autre ?
A part ça, il n’est absolument pas question de « peuple élu » ou de dictature ou quoi que ce soit dans l’attitude de mes collègues, je clarifie:
99% des résultats de mathématiques ne sont jamais vulgarisés, parce qu’ils sont trop techniques et/ou ne présentent pas d’intérêt pour le grand public. Il suffit de se demander qui parmi les non-mathématiciens a ne serait-ce qu’une vague idée de ce que les médaillés Fields ont fait, et on est vite fixé. Ce n’est pas de la mauvaise volonté, c’est naturel que certains travaux se prêtent mal à la vulgarisation, même s’ils sont célèbres parmi les mathématiciens.De la même manière que personne ne découvre la physique en commençant par la théorie quantique des champs ou je ne sais quel domaine ultra-pointu, et ca vaut pour n’importe quel autre domaine où un certain bagage est nécessaire pour comprendre les concepts manipulés. Certaines personnes pensent juste que le théorème de Gödel devrait rentrer dans cette catégorie. Surtout que le danger additionnel au fait de simplement ne pas comprendre le théorème de Gödel, c’est surtout de mal le comprendre, et de l’appliquer à tout va n’importe comment (cf Debray).
Sur le premier point : seul un système logique monadique est complet. (récursif). On ne peut pas avec un tel système sortir du domaine d’interprétation (0% de métalangage). Pour pouvoir sortir du domaine de l’interprétation alors il faut aller au-delà et alors on tombe dans le non récursif donc au mieux dans le semi-décidable (récursivement axiomatisable) mais on peut rester dans le consistant. il faut aller jusqu’à formaliser l’arithmétique au sens de Gödel pour pouvoir s’affranchir complétement du domaine d’interprétation (100% de métalangage) mais alors la consistance n’est plus assurée (second théorême). Je crois que c’est toi qui fait une confusion entre la complétude et la consistance.
On pourrait de la même façon dire que ℝ est le dernier corps commutatif archimédien et complet. Cependant, il n’est pas algébriquement clos. C est clos mais la relation d’ordre n’est plus assurée.
Sur le second point : la peur n’exclu le danger.
Bon je crois que je vais abandonner, j’ai l’impression que tu ne lis pas mes commentaires. Je te mets ci-dessous quelques définitions (que tu peux vérifier sur internet) à la lumière desquelles tu peux relire la discussion ci-dessus.
Théorèmes de complétude et d’incomplétude: parlent de la logique du premier ordre (et c’est tout!), sur l’univers des nombres entiers.
Logique du premier ordre: on ne peut quantifier que sur les variables, c’est-à-dire les éléments de l’univers: il existe x, blabla.
Logique monadique du second ordre: on peut quantifier également sur les ensembles d’éléments. En particulier « monadique » n’a pas de sens pour la logique du premier ordre, donc ton commentaire ci-dessus n’en a pas non plus, puisque tu places la logique monadique en-dessous de celle utilisée dans le théorème de Gödel, qui est du premier ordre.
Logique du second ordre: on peut également quantifier sur les relations R(x,y,z) entre les éléments. « monadique » revient à se limiter aux relations E(x) d’arité 1, qui sont équivalentes aux ensembles. Typiquement on peut dire: « il existe une fonction telle que blabla ».
Logiques d’ordre supérieur: on peut quantifier sur les relations entre ces relations, etc…
A titre d’exemple, on ne peut pas dire qu’un graphe est connexe avec la logique du premier ordre, puisqu’on est obligé de parler de « chemin » d’un point à un autre, ce qui requiert un ensemble de sommets. On peut dire par contre au premier ordre qu’aucun sommet n’est isolé, ou qu’il existe un cycle de longueur 3.
Tu parles de Tarski : et bien justement on a le langage objet qui peut être complet et consistant et le métalangage qui est sémantiquement clos mais qui ne peut être à la fois consistant et complet. Ce n’est pas par ce qu’un système n’est pas complet que sa consistance est indécidable.
Tu peux clarifier stp ? Quel est le rapport avec Tarski ? Tu te réfères au paradoxe de Banach-Tarski ou à autre chose? Quel est la définition de « langage objet » (j’imagine que tu ne parle pas de programmation), de « métalangage » et de « sémantiquement clos » ?
A propos de ta phrase « Ce n’est pas par ce qu’un système n’est pas complet que sa consistance est indécidable. », tu as un exemple ?
La théorie des corps algébriquement clos n’est pas complète, puisque la caractéristique mais elle est décidable.
La théorie des corps algébriquement clos n’est pas complète, puisque la caractéristique n’est pas précisée, mais elle est décidable.
Vos joutes mathématiques sont très amusantes, mais il faut prendre un peu de hauteur messieurs.
Le théorème de Gödel a surtout une signification sur le statut des mathématiques parmi les sciences et les connaissances.
Même si le théorème de Gödel ne s’applique formellement que dans le cadre des mathématiques ou même que d’une théorie mathématique, ou même que d’une seule théorie mathématique (l’arithmétique par exemple), il suffit d’un peu de bon sens pour comprendre que cela signifie que la pure logique ne peut pas tout démontrer, a fortiori dans le monde réel qui est forcément encore plus complexe que n’importe quelle théorie mathématique.
Le fait que la « pure logique » ne peut pas tout démontrer est un débat philosophique qui a peu à voir avec le théorème de Gödel. D’ailleurs ce que tu dis relève plutôt du théorème de complétude, qui dit que la pure logique (dans un sens précis) est capable de tout démontrer (explorer toutes les conséquences d’axiomes donnés). Donc à mon sens tu prends le théorème d’incomplétude pour supporter ton argumentation plutôt que le théorème de complétude parce que ton avis sur la question était de toute manière déjà formé, et tu prétends le confirmer avec un résultat mathématique complètement sorti de son contexte. Je peux argumenter le contraire de ce que tu affirmes: « d’après le fameux théorème de complétude de Gödel, la pure logique PEUT démontrer tout ce qui est vrai dans le monde réel » et tu serais à mon avis bien en peine de répondre.
En réponse au dernier commentaire d’Axel: « La théorie des corps algébriquement clos n’est pas complète, puisque la caractéristique n’est pas précisée, mais elle est décidable. »
« Complète » et « Décidable » sont synonymes quand on parle d’une théorie. Le fait qu’on ne puisse pas déduire la caractéristique vient du fait que celle-ci n’est pas exprimable dans le langage de la théorie, et ne prouve pas que la théorie est incomplète.
Quand je parle de langage-objet c’est au sens de Tarski (je ne parle pas de langage orienté objet). Le langage objet c’est celui qui permet une logique de premier ordre complète au sens de Gödel (1929). C’est la vérité relative aux axiomes (dénombrable) : on ne sort pas du « domaine de l’interprétation ». Si on veut sortir du domaine de l’interprétation, il faut un métalangage : la vérité n’est plus relative mais absolue. On construit alors des phrases du type « menteur » : « »2+2=4″ est une proposition vrai ».
Ce que Tarski appelle « clôture sémantique » c’est exactement identique que la clôture algébrique des Réels sur les Complexes. Gödel cherchait à voir ce qui se passait quand on utilisait « un langage objet » pour en faire également un « métalangage » (c’est le même langage qui sert pour les 2″. Il formalise alors une phrase du type « paradoxe de Richard » et constate que la « clôture sémantique » ne peut à la fois être complète et consistante et que la consistance est même indécidable. On n’est pas dans le relatif mais dans l’absolu.
Ensuite, Gödel ne s’applique pas qu’à l’arithmétique. Si Gödel dit « capable de formaliser l’arithmétique des entiers naturels » c’est que cette condition est nécessaire pour procéder à la clôture sémantique. Enfin, si Gödel s’applique de façon large c’est que tout langage est mathématique : le plus simple étant le langage binaire.
Ce ne sont pas des joutes mathématiques : c’est juste qu’il faut bien comprendre Gödel et que ce n’est pas forcément intuitif (et je ne dis pas que je détiens la vérité tant cela est un changement complet du paradigme…).
Denis : je suis d’accord mais R n’est pas algébriquement clos.
cf. http://fr.wikipedia.org/wiki/Fermeture_de_Kleene
« La théorie des corps algébriquement clos n’est pas complète, puisque la caractéristique n’est pas précisée, mais elle est décidable » : je voulais dire effectivement semi-décidable c’est à dire récursivement énumérable.
On peut effectivement choisir entre i^2 et i^1/2 pour -1. Canoniquement on choisit i^2 mais il existe un foncteur d’oubli : par oubli de structure, on choisit de considérer que la variété complexe de dimension 1.se présente comme une variété différentielle réelle de dimension 2.
Je pense que ce paragraphe résume le noeud de notre désaccord:
« Ce que Tarski appelle « clôture sémantique » c’est exactement identique que la clôture algébrique des Réels sur les Complexes. Gödel cherchait à voir ce qui se passait quand on utilisait « un langage objet » pour en faire également un « métalangage » (c’est le même langage qui sert pour les 2″. Il formalise alors une phrase du type « paradoxe de Richard » et constate que la « clôture sémantique » ne peut à la fois être complète et consistante et que la consistance est même indécidable. On n’est pas dans le relatif mais dans l’absolu. »
Apparemment tu penses que pour passer du « langage objet » à un langage capable de parler de lui-même, il faut rajouter des choses, et faire une opération de « clôture sémantique » qui s’apparente à la clôture algébrique qu’on fait pour passer de R à C. Tu sembles quand même mentionner que « c’est le meme langage qui sert pour les 2 », donc ton opinion n’est pas très claire. (Je ne vois pas le rapport avec la fermeture de Kleene que tu postes dans le commentaire suivant.)
Bref je veux insister sur le fait que quand on passe de R à C, on rajoute des choses nouvelles. Or dans une théorie du premier ordre qui contient l’arithmétique, il n’y a rien besoin de rajouter pour obtenir l’auto-référence et donc l’indécidabilité! Le métalangage est déjà contenu dedans « par défaut », via l’encodage de Gödel.
Pour être plus précis, si K est un corps, « clôture algébrique de K » désigne un sur-ensemble de K: le plus petit corps qui contient K et qui est algébriquement clos. En revanche, il n’y a pas de telle opération appelée « clôture sémantique » à laquelle tu sembles faire référence (je me trompe peut-être, auquel cas je serais très intéressé par un lien), et qui augmente un langage formel de manière à ce qu’il puisse parler de lui-même.
Mais justement on ne rajoute rien quand on passe de R à C : on perd le caractère archimédien ! La clôture algébrique n’est pas une clôture différentielle (elle n’est pas stable).
Quand on passe de R à C on rajoute des éléments (les nombres complexes). Ce n’est pas le même ensemble: R est strictement contenu dans C, donc faire la clôture algébrique correspond à ajouter des éléments. En général, « clôture » en mathématiques signifie » si l’ensemble n’est pas clos pour certaines opérations, on ajoute le moins d’éléments possible pour qu’il le soit ». Tu sembles penser que « clôture sémantique » est une opération de ce type, mais ce n’est pas le cas.
Tu confonds en fait clôture algébrique et clôture différentielle… Cette conversation est stérile : oui effectivement C contient strictement R et on ajoute i comme on ajoute epsilon pour la fermeture de Kleene.
Excuse moi mais c’est toi qui as parlé de clôture algébrique : « Ce que Tarski appelle « clôture sémantique » c’est exactement identique que la clôture algébrique des Réels sur les Complexes. ».
Bon on est au moins d’accord que la conversation est stérile, on peut en rester là…
R est le premier corps complet au sens de Cauchy (semi-décidable), de caractéristique nulle (qui contient donc une copie de Q le premier corps de caractéristique nulle), et le dernier corps archimédien (semi-consistant). R contient également une copie du corps des nombres algébriques qui est lui archimédien.
Complémentarité = conjugaison dans le cadre le cadre de la clôture algébrique de Q. Mais, comme Q n’est pas semi-décidable pas de récursivité possible.
Complémentarité pas = conjugaison pour la cloture de R car C n’est pas archimédien.
Concernant l’article:
Je me pose également la question d’une théorie à laquelle on ajouterait un axiome qui se trouve être une proposition fausse et indémontrable.
Je n’ai pas trouvé de reponce et la tienne ne me convient pas, en effet:
Ajouter au 4 premiers axiomes d’Euclide celui des parallèles ou sa négation ne constitue pas deux modèles différent d’une même théorie mais deux théories différentes.
j’comprends pas le deuxième theoreme , aucun synthaxe claire ne peut l’expliquer?
A reblogué ceci sur Idées & Sciences.
Impressionnant … J’avais moi-même découvert ce théorème un peu par hasard sur internet mais voici un article très complet et clair ! Félicitations ! La question est immense quand même… Trouverons-nous un jour la réponse ?
Pingback: Musique au FNC-2014 | A r t s & S c i e n c e s
Très chouette, mais sur 2000 mots j’ai du lâcher vers 1500 dommage…
Bonjour,
Au sujet de cet article et pour bien clarifier les chose, il faut bien faire la différence entre le « démontré » (notion syntaxique), le « vérifié » et le « vrai » (notions sémantiques). Au regard d’une théorie, on dit qu’une proposition est vraie si et seulement si tous les modèles de cette théorie la vérifient ; et on dit qu’une proposition est fausse si est seulement si aucun de ces modèles ne la vérifient. Du coup, le « vrai » n’est pas la négation du « faut » ! Une proposition n’est pas fausse si et seulement si il existe au moins un modèle qui la vérifie (ce qui n’est pas la définition du « vrai » !).
Quant Gödel démontre que dans l’arithmétique de Peano [PA] :
« Il existe une proposition G, telle que : G est démontrable si et seulement si G est fausse »
Il démontre, par contraposée, que :
« Il existe une proposition G, telle que : G n’est pas démontrable si et seulement si G est vérifiée dans au moins un modèle (i.e. n’est pas fausse) de PA »
Autrement dit, G sera vérifiée ou falsifiée (de façon exclusive et certaine) au regard d’un modèle donnée de la théorie, mais indécidable (i.e. ni vraie, ni fausse) au regard de la théorie. Et c’est cela l’incomplétude.
Attention: G N’EST PAS VRAIE, G N’EST PAS FAUSSE, G EST I-N-D-E-C-I-D-A-B-L-E !
Ce faisant, Gödel ne démontre pas qu’il existe des propositions vraies qui ne soient pas démontrable. Si c’était le cas, il aurait rien moins que démontré que l’arithmétique était inconsistante . Ce qu’il démontre, c’est qu’elle est incomplète et incomplètable (puisque cette démonstration se fait au sein même de la théorie)… sous l’hypothèse qu’elle soit consistante (i.e. cohérente).
Cordialement,
Valdo.
Une proposition générale circonstancielle précise comme un théorème , est fausse si UNE SEULE application particulière est fausse ..
Vous l’ avez vous même utilisé dans bien des démo = Il suffit d’en trouver UNE qui est fausse pour pouvoir nier la vérité énoncée .
L’insistance sur le caractère purement mathématique, voire arithmétique, du théorème d’incomplétude m’étonne. Le langage des math est souvent considéré comme pur même s’il reste un langage.
Comment se fait-il que personne ne semble s’arrêter au paradoxe du second théorème, qui postule qu’on ne peut pas démontrer la consistance d’un système formel en restant à l’intérieur de celui-ci.
Faut dire que ça réduit toutes ces causeries à du babillage.
Outre le fait que l’énoncé du second théorème d’incomplétude de Gödel que vous faites semble déborder largement de ce qu’il est réellement, de façon général, en quoi serait-il paradoxale qu’un système formel donné ne puisse pas démontrer sa propre consistance ? Quel paradoxe introduirait un tel système ?
Pour pouvoir décrire une situation, un univers, il faudrait pouvoir s’en extraire sinon on tourne en rond. L’outil qu’on utilise, le langage fait partie du problème qu’on tente de décrire.
Pingback: Les impossibles 1 | Pourquoi Comment Combien
Pingback: Incomplétude 4 | Science-innocence
Merci pierre jenny, je ne suis ni mathématicien ni logicien et j’avoue ne maitriser que peu des aspects techniques évoqués plus haut, mais j’avais quand même bien compris ce que vous venez de dire et malgré les précédents commentaires je pense que ce théorème peut s’appliquer a bien des situations autres que mathématiques. Il existe d’ailleur un écrivain réputé qui montre les correlation du théorème d’incompletude avec la musique de Bach, les dessins d’un certain Escher et la conscience de soi. Il en parle comme appartenant aux concept de boucle étrange. Je ne possede peut etre les compétences techniques pour appréhender les parties pointues du théorème mais je pense avoir bien compris le concept peut être justement pour cette raison ; ) .Sinon je m’intéresse au sujet car je souhaite me faire tatouer un serpent qui se mort la queue et que ce symbole me fait réfléchir depuis longtemps et je fut agréablement surpris de voir que je ne suis pas le seul a être obnubilé par ce concept et que même certain mathématicien y on dévoué leurs recherches ; ). J’espère ne pas trop avoir abaissé le niveau du débat. Cordialement
Voir les commentaire de Girard sur Gödel-Escher-Bach, c’est rigolo (il allume le livre et Escher qu’il traite de… non je ne peux pas le dire), et à mon avis pas faux…
salut gg.
franchement, je ne comprends à peu près rien au maths et à ce qui se dit sur ce billet.
J’ai juste l’impression que la « réalité » est appréhendée par chacun comme autant de « vérités » qui ne sont finalement que des convictions personnelles largement influencées par des éléments « extérieurs ».
Beaucoup de guillemets pour inciter à la prudence sémantique.
Tout ce que m’a inspiré Gödel, c’est la modestie et l’humilité. Mais surtout, il m’a libéré en grande partie de ma culpabilité.
Avec Benjamin Libet qui nous assure que le corps décide avant le cerveau.
Mais…. j’y pense. L’auteur de ce blog s’est-il déjà penché sur le libre arbitre ?
J’adorerais qu’il intervienne.
Salut, je me pointe en retard !
Il y a énormément d’énoncé « concrets » et indécidable. Les mathématiciens et les informaticiens le démontrent fréquemment.
De plus, on ne peut pas dire que le théorème de Gödel est une « claque » pour les mathématiciens.
Pour Papy Hilbert, certainement.
Pour les autres, c’est LE CONTRAIRE !!!!
On peut interpréter ce théorème comme l’affirmation que jamais une machine ne saurait remplacer un mathématicien : il n’existe pas de programme qui liste tous les théorèmes vrais de ZF (bien entendu un tel programme tournerait indéfiniment, mais donnerait pour tout toute affirmation vraie une preuve en temps finie).
Plutôt rassurant non ? Quoiqu’il arrive, les matheux ne seront pas remplacés par des machines. Tout le monde ne peut pas en dire autant… (c’est pas une raison pour devenir prétentieux les matheux 😉 )
Une autre manière de le voir (celle de Gödel je crois) est de dire qu’il faut rajouter des axiomes à ZF pour résoudre certains problèmes.
En effet, les mathématiciens étudient des modèles, et dans un modèle une proposition est vraie ou fausse. Il paraît donc logique de compléter l’axiomatisation avec des axiomes « naturels » quand on a affaire à une proposition indécidable pour dénouer le vrai du faux !!!
C’est ce qui se fait par exemple avec l’hypothèse du continu. On rajoute des axiomes de grands cardinaux, d’autres trucs liés au Forcing de Cohen, et on essaie de montrer que l’hypothèse est fausse (il semblerait qu’il y ait un (unique) cardinal entre card(N) et card(R))
Belle tentative de vulgarisation, mais perso je vous conseillerais plutôt les nombreux articles de JP « Starivore » Delahaye, un peu plus ardus mais nettement plus précis !
DSM
PS : j’ai vraiment pas tout lu, désolé si je ressasse du déjà dit ici…
J’aurais pas dû parler d’indécidabilité au sens informatique…
Et il existe une machine qui liste toute les preuves correctes dans ZF, c’est bien le minimum !!!!
Et rajouter des axiomes à ZF pour démontrer quelque chose, ça doit pas plaire à tout le monde.
J’aurais vraiment dû me taire… Et comme je ne peux pas supprimer ce message, je vous prie de m’excuser.
je lis le début
ça commence mal
il es écrit
ces propositions sont tellement tordues qu’on ne les rencontrent jamais
or, on ne rencontre que ça
c’est pourquoi il est inventé des théories bizarres dont Einstein
des theories qui ne comprennent rien et en font une science comme les quanta
d’autres
et que l’on assiste à l’invention de la notion de systémes complexes
ces situations indémontrables mais réelles sont 100 fois plus courantes réalistes et nombreuses que celles que les mathématiques résolvent
Je trouve que cet article explique très bien le théorème de Gödel. Je suis une élève de terminale S et je devais faire une dissertation sur la démonstration, comprenant ce théorème et, grâce aux explications bien précises et claires, je dois dire que j’ai parfaitement compris du sujet. Je n’ai pas l’habitude de commenter mais comme c’est un article qui explique très bien le sujet, je tenais à le faire savoir à la personne qui a rédigé cet article.
Cordialement
Merci d’avoir pris le temps de le dire !
J’aurais aussi apprécié que David prenne le temps de commenter pour les profanes, interpellés par des questions qui semblent déranger certains scientifiques. Notamment les timides suggestions dans la foulée des découvertes d’Alain Aspect sur la question des univers parallèles en physique quantique, ou plus simplement ici, la pertinence d’analyser un sujet avec des données qui font partie du sujet.
Pingback: Avgritche | Pearltrees
Pingback: The Reference Frame: L’ équation Bogdanov | Thomassonjeanmicl's Blog
Pingback: Gödel | Pearltrees
Pingback: Logique - jlj | Pearltrees
Pingback: La rétro-causalité INTRODUCTION | Thomassonjeanmicl's Blog
ca serait bien de pas melanger la calculabilite, l’incompletude, et l’independance des axiomes… ce que ce post reussit a joyeusement faire…
Je ne suis pas sûr de comprendre votre commentaire…mais je veux bien que vous m’en disiez un peu plus !
Le pire est lorsque les maths démontrent quelque chose qui est foncièrement impossible, donc faux.
Exemple:
Il est mathématiquement démontrable qu »un sac contenant trois pommes duquel on retire cinq pommes contient maintenant moins deux pommes. Mais je ne crois pas un jour rencontrer un tel sac. 🙂
Bonjour . Pour ma part j’ai arrêté les maths en première année de fac pour ne les reprendre que … maintenant ( en gros ), comme autodidacte . Sans m’étendre sur le sujet mon parcours est un peu particulier . Dans ce contexte il me manque encore la maîtrise de beaucoup d’outils pour parler votre langage, si tant est que je puisse l’adopter tel quel un jour . Néanmoins .. il y a un point ( un notamment pour commencer ) qui m’interpelle : de ce que je vois Gödel valide sa théorie par des propriétés ou » métapropriétés » (?) ( indécidabilité, incomplétude, inconsistance et leur vis-à-vis respectif contraire ou/et contradictoire ) découlant de propriétés de systèmes formels » décidés » ( ZF, Peano ou autre ) donc toute conclusion non seulement découle mais est finalement prioritairement et mécaniquement soumise à la valeur accordée au système formel » parent » ou » juge « , dans la démonstration . Si ça tient suffisamment jusque là ça veut dire tout de même au moins deux choses : tout d’abord que ( pour réduire le truc ) P’ indécidable vient de P décidable ( le » système axiomatique juge » qui gère la démonstration ) et deuxièmement ( un corollaire à cette idée ) que l’indécidabilité d’une proposition ne vient pas de son caractère indécidable en lui-même … donc il peut tout à fait s’avérer l’être ( décidable ) si des fondements du système parent s’avèrent au moins indécidables dans le cadre restreint de l’énonciation de son ( ou ses ) hypothèse(s) de départ ( révélé par des failles dans les prédicats ou les propriétés des outils classiques – .. et, inclu, exclu … même ( et peut-être surtout ) vrai et faux – pour l’édifier ) . Pour le mettre en image je le formulerais peut-être de cette façon : Est-ce que P vrai est décidable ? …Mais je reconnais : je ne sais pas si la formulation convient, l’idée a pu être évoquée autrement ou je peux tout à fait être hors sujet ! Mais sinon ça implique potentiellement de reconnaître naturellement la part subjective ( mais pas nécessairement fausse ^^ ) de tout consensus à priori objectif . ( j’attends les cailloux 😛 )
de même que pour décrire la complexité du réel on a créé des nombres à deux dimensions dont une des parties dépend de i, racine carrée de -1, le nombre dit imaginaire. Ce qui valide pour moi votre conclusion : pour décrire la complexité de ce qui est on multiplie un nombre réel par l’imagination (objectif/subjectif) les deux étant les deux faces d’une même pièce.
Excusez moi pour cette question primate, mais le mot » consistant » que vous employez n’est-il pas une reproduction légèrement » faux-sens » de l’ anglais » consistent » dont le sens réel en Français serait » cohérent » ?.
Le sens de votre explication ( d’ excellente didactique ) serait alors que l’ alternative de ces vérités étudiées resterait enfermée dans l’ ensemble à deux élément : [ : non démontrable , incohérente . ]
Ex : Une transposition logique établie entre [ je suis un menteur ] et [ je ne peux pas être un menteur ]
Merci .
Pingback: Igor et Grichka Bogdanoff | Pearltrees
Pingback: Rien de nouveau depuis 1931 « Les Vérités Scientifiques
Pour ma part, peu matheux, vous n’avez juste pas abordé avec assez de force, l’aspect le plus intéressant. Si il existe des assertions vraies mais indémontrables, alors tant qu’elle ne sont pas démontrées, on ne sais pas si elle sont vraies ou fausses et leur contraire a autant de valeur. Aussi, je peux construire n’importe quel système d’axiomes consistants il a autant d’intérêt que les autres et aussi indémontrable. Il n’y a pas une vérité mais différents états de vérité qui peuvent se côtoyer. La démonstration a lieu en trouvant un ensemble plus grand. Ce qui semble dire que pour démontrer notre univers il faudra en sortir … tant que ce n’est pas fait, impossible de savoir si on est dans Matrix … et penser que les fenêtres les plus hautes ne sont sont pas intéressantes, n’a rien de mathématique mais tout d’une manière d’essayer de se rassurer pour ne pas voir leur croyances s’effondrer ? non ?
Bien évidemment je peux vous affirmer en vous contredisant sans risque qu’en restant dans notre univers il n’y a qu’une seule vérité ! Et toutes les assertions vraies sont démontrables. Ce que dit juste GODEL est que pour certaines il faut enrichir la base axiomatique du système mathématique dans lequel on travaille pour arriver à établir la démonstration.
En poussant le raisonnement et pour s’amuser, prenons par exemple la méta-proposition « Dieu existe ». D’après GODEL, elle ou son contraire devrait donc être démontrable, à condition expresse d’utiliser un système axiomique cohérent et suffisant !
Pingback: article 4) Perdons-nous connaissance? Troisième partie chapitres 1 et 2 | Thomassonjeanmicl's Blog
En vérité le Théorème de Gödel n’est qu’un Axiome!Pour le comprendre il faut remonter au célébrissime Cinquième Postulat dit axiome d’Euclide . Ce Axiome qui n’en était pas un , avait occupé les mathématiciens durant plus de deux milles ans dans le but d’en faire
un Théorème . Et, brusquement , au lieu de tomber sur un Théorème
semblable à celui de Gödel ils tombèrent sur une découverte abusivement appelée géométrie non euclidienne. C’était une échappatoire que le Théorème de Gödel a fini par rattraper et réhabilite par la même occasion Euclide. Gödel avait réhabilité Euclide pour une raison simple : le Cinquième Postulat fut en réalité une Question et non un Axiome. Au total il s’agit de faire la distinction entre le dénombrable et l’indénombrable alors que les deux sont des infinis…Mohwali Awamar
Bonjour.Tout est passionnant dans vos commentaires et réflexions.Gödel montre ce que nous sommes,des créateurs de théories intéressantes et formidables.Il pose comme nos enfants une question intelligente ,mais nos arguments nos réponses se compléteront indéfiniment sans atteindre l’infini.la seule certitude que nous avons aujourd’hui c’est que nous mourrons ,et si un jour nous serons éternels d’autres problèmes se poserons.Quoique je fasse je n’ai pas la prétention d’atteindre les sommets de l’ignorance.C’est peut-être une chance d’être idiot.Mais continuons d’avancer .Cordialement.
Pingback: Penser n’est pas calculer : l’échec du logicisme. | L'Autreté
Pingback: La renaissance du temps : épilogue | Thomassonjeanmicl's Blog
Pingback: Igor et Grichka Bogdanov | Pearltrees
C’est un peu idiot mais au fond GODEL a inventé l’eau tiède car dans tout système mathématique il existe toujours des énoncés vrais indémontrables puisque déjà tous les axiomes du dit système sont à ranger dans cette catégorie. Bon, en fait ce qu’il a découvert c’est qu’il y en avait forcément d’autres et qu’aucun système, aussi riche en axiomes soit-il, ne sera jamais tout à fait complet.
Que les axiomes soient vrais et indémontrables est troublant. En effet, puisqu’ils sont indémontrables alors comment sait-on qu’ils sont vrais ? Le sait-on seulement parce que l’évidence s’impose ? Par 2 points il y a toujours une droite qui passe ? Oui, c’est évident à notre esprit sans avoir besoin de plus de démonstration…
En fait, un axiome n’est pas un énoncé appelant une justification mais une hypothèse basique de départ consistant en une proposition première sur laquelle le système axiomatique sera bâti. Il est évidemment souhaitable que cette proposition première soit vrai sinon le système construit court à la catastrophe. En réalité, dire que les axiomes ne sont pas démontrables est aller trop vite en besogne. Il est facile de prouver par l’absurde qu’il est toujours possible de faire passer une droite par 2 points. Vous n’arriverez jamais à prouver qu’on ne peut pas ou qu’il est possible d’en faire passer plus d’une à moins de renier la réalité ou tout du moins la perception que l’on en a.
Non, Godel n’a pas démontré l’eau tiède !
Justement, son système est récursivement axiomatisable, c’est à dire que le statut des axiomes n’est pas différent de celui d’une proposition induite (théorème). Golem avait démontré qu’un système du premier ordre était complet. Si on veut qu’il soit en plus récursivement axiomatisable alors il est soit incohérent (c’est à dire absolument indecidable du fait du principe de l’explosion logique) soit incomplet. On pourrait aussi dire qu’un système du premier ordre n’est pas en mesure d’axiomatiser un système récursivement décidable (c’est à dire capable d’axiomatiser l’arithmétique) complet (et donc consistant).
Ce qui fait le génial de Godel, c’est qu’il démontre ça dans un système logique du premier ordre (car ce système est complet donc capable de démontrer ce qu’il n’est pas en mesure de démontrer).
Pingback: Gödel : Mon article 1: Gödel et ses démons anticipent le problème de Turing? | Thomassonjeanmicl's Blog
Que signifie un énoncé VRAI non démontrable? Quel critère a donc pu garantir sa véracité? Si l’énoncé est vrai (pour un système d’axiomes), c’est qu’il en existe une démonstration (dans ce système). Ce que dit le théorème de Gödel, c’est que dans tout système d’axiome suffisamment développé pour contenir l’arithmétique, il y a des énoncés qu’on ne peut démontrer et dont on ne peut démontrer la négation. Ces énoncés sont dits indécidables.
Vous pouvez aller voir ce billet (plus récent) où je développe la notion de modèle
https://scienceetonnante.com/2016/12/09/theoreme-godel/
En gros la notion de « démontrabilité » est relative à un système d’axiomes, celle de « vérité » à un modèle
Bonjour,
Juste une petite remarque qui m’a troublée dans votre article sur le théorème d’incomplétude de Godël.
Pourquoi vous dites souvent qu’une proposition indécidable dans une théorie cohérente est une proposition vraie mais non démontrable dans cette théorie !
Une proposition indécidable est plutôt ni vraie ni fausse. On ne peut pas ni la démontrer ni démontrer sa négation et on peut effectivement l’ajouter aux axiomes de la théorie en question ou ajouter sa négation en maintenant le caractère cohérent de la théorie initiale mais qui bien sûr est une nouvelle théorie. Nous sommes bien d’accord (il me semble que oui par rapport à votre article suivant sur les modèles) ?
Oui absolumenent, quand je dis « vrai » ici je suis imprécis, il faut plutôt entendre « vrai dans le modèle « naturel » que l’on a en tête, par exemple l’arithmétique ».
> Mais pour les mathématiques de la théorie des ensemble, quel est le modèle raisonnable qui nous dit ce qui est vrai et ce qui est faux ? Une solution serait le modèle de l’Univers Constructible de Gödel, dans lequel l’axiome du choix (comme l’hypothèse du continu) sont « vrais » … mais je ne suis pas sûr de comprendre pourquoi !
La plupart des mathématiciens qui connaissent la question ne croient pas à l’axiome de constructibilité. En gros, ça veut dire qu’ils rejettent l’idée que l’univers constructible serait le modèle canonique de ZFC. Mais c’est un énorme sujet de débat.
Pour un peu de vulgarisation à ce sujet (quand même beaucoup plus technique que votre site), je renvoie à http://www.madore.org/~david/weblog/d.2013-03-19.2124.constructible.html#d.2013-03-19.2124 , sur le blog de David Madore que je recommande chaudement au passage.