Hier soir, vous avez organisé une petite fête et invité une vingtaine d’amis. Alors qu’au milieu de la soirée, la conversation tourne (allez savoir pourquoi) sur les signes du zodiaque, deux de vos invités découvrent avec stupeur que leur anniversaire tombe le même jour !
– Incroyable !
– Ah oui, quelle coïncidence !
– Tu imagines la probabilité que ça arrive ?
Eh bien justement, parlons en de la probabilité !
Il se trouve qu’elle n’est pas du tout négligeable : dans un groupe d’environ 25 personnes, il y a plus de 50% de chance que deux de ces personnes soient nées le même jour. Ce résultat est tellement contraire à notre intuition qu’on l’appelle le paradoxe des anniversaires.
Pour les incrédules et les lycéens qui révisent les probas pour le bac, faisons ensemble le calcul pour un groupe de N personnes. Pour faire cela, on va prendre le problème à l’envers, et calculer la probabilité P que toutes les personnes aient leur anniversaire un jour différent. Et pour calculer cette probabilité, on va classiquement procéder par dénombrement.
Commençons par l’ensemble de tous les cas possibles : pour la première personne, 365 dates sont possibles, pour la seconde aussi, de même que pour la troisième et toutes les autres. Si on multiplie tout ça il y a donc \(365^N\) cas possibles.
Maintenant quels sont les cas où les anniversaires sont tous différents : pour la première personne il y a 365 choix, pour la seconde il n’en reste que 364, pour la troisième 363, etc. et pour la Nième seulement (365-N+1). Si on multiplie tout ça on trouve la quantité \(365! / (365-N)!\) (pour les lycéens, celle qu’on note parfois A(365,N), le nombre d’arrangements).
On peut donc calculer notre probabilité P qui vaut
\(P = \frac{365!}{365^N (365-N)!}\)
J’espère que vous me croyez pour l’application numérique, mais avec N=23 personnes on trouve P = 0,49. Mais rappelez vous que P est la probabilité que les anniversaires soient tous différents. Donc la probabilité qu’il y en ait au moins deux identiques est 1 – P, soit ici 0,51, c’est-à-dire 51% de chance !
Et plus il y a de personnes dans le groupe, plus cette probabilité augmente. Dans un groupe de 50 personnes, il y a plus de 95% de chance que deux personnes aient leur anniversaire le même jour.
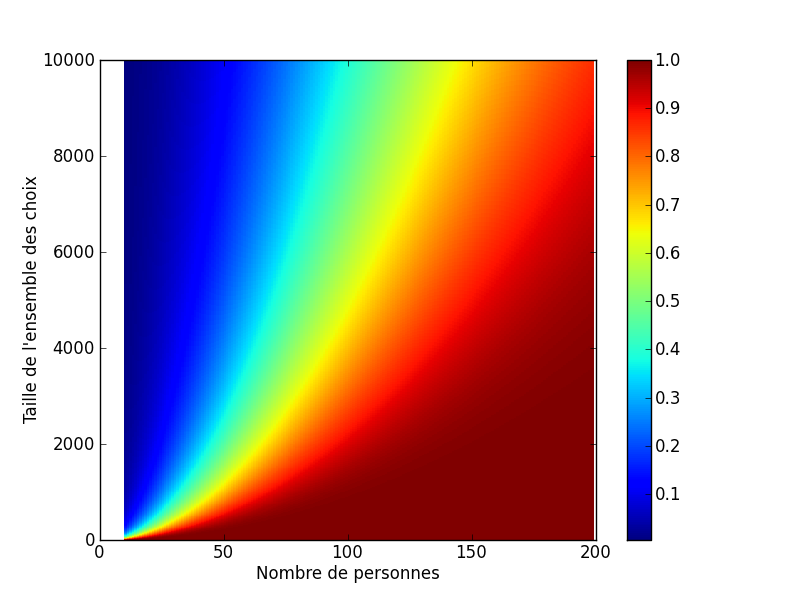
Pour trouver d’autres paradoxes de ce genre, on peut calculer la probabilité en remplaçant 365 par n’importe quel nombre K, et pour n’importe quelle taille de groupe N. Le résultat est représenté dans le graphique ci-dessous, la couleur indiquant la probalité que 2 personnes au moins parmi les N aient une caractéristique identique, celle-ci étant prise dans un ensemble de taille K.
Prenons un exemple précis : il y a 365 jours dans l’année et 24 heures par jour, soit au total 8760 tranches horaires pour naître dans l’année. Le graphique montre que dès que vous réunissez une centaine de personnes, il y a plus de 50% de chance que deux personnes soient nées le même jour dans la même tranche horaire ! Encore un résultat contre-intuitif, qui justifie l’appellation de paradoxe !
Ah oui, sinon c’est mon anniversaire cette semaine 🙂
Pour aller plus loin…
Quelques considérations pour les plus curieux. Tout d’abord, ce raisonnement ne vaut que si les N personnes ont leur jour de naissance distribué de façon uniforme dans l’ensemble des possibles. On sait pour les naissances que c’est en gros le cas, mais le raisonnement ne tient pas par exemple avec les prénoms.
Petite précision technique : pour réaliser le graphique, je n’ai pas fait le calcul direct de la probabilité, mais je suis passé par son logarithme. Ça marche très bien grâce à la formule de Stirling qui donne une excellente approximation de N! dès que N dépasse 10, et ça évite de manipuler des chiffres astronomiques du genre la factorielle de 10000.
Il existe une application concrète de ce paradoxe, où plutôt de la nécessité de l’éviter. Comme vous le savez peut être, il existe des méthodes (comme le « MD5 checksum ») qui permettent d’associer un identifiant numérique à un fichier. Si vous voulez que ce nombre identifie de manière quasi-unique ce fichier parmi tous vos fichiers, vous devez vous assurer que la probabilité que deux fichiers différents aient le même MD5 soit suffisamment faible. Cela fixe la taille K de l’ensemble des identifiants. Si vous avez N fichiers, il faut prendre K suffisamment grand pour que p(N,K) soit suffisamment faible. Comme le montre la carte colorée, dès que N devient grand il faut aller chercher des K astronomiques pour avoir des probas de conflit disons de 1% ! Pour le MD5, il y 2^128 combinaisons, environ 10^38 !
A lire aussi : Le billet de ElJJ « Une chance sur beaucoup« , où l’on apprend entre autre qu’il y a 200 fois plus de chance de gagner au loto que de réunir 120 personnes sans qu’aucune n’ait son anniversaire le même jour qu’une autre…
35 Comments
Joyeux anniversaire en avance dans ce cas ! 😀
Un grand classique, j’aurais juré que vous l’aviez fait, mais non ! En tout cas, il ouvre d’autres horizons sur l’application, et c’est ce qui fait le petit plus qui vous caractérise ! Bravo !
amusant, cela rend les stats plus concrètes (et trop fière j’ai quasiment tout suivi du début à la fin sans difficulté)
merci pour cet article une fois encore original et bien construit
Bon anniversaire en avance aussi, j’aime votre blog que j’ai découvert récemment, très sympa!
Joyeux anniversaire aussi ! Un peu dommage que je connaisse déjà ce paradoxe … mais par contre le lien à la fin de l’article est super ! 🙂
Excellent article! Et pour les années bissextile? 😀
Joyeux anniversaire!
Il me semble que ce résultat parait paradoxal lorsque l’on compare 25 (le nombre de personne) à 1/365 (la probabilité que deux personnes fixées aient leur anniversaire le même jour) : le produit est petit.
Le résultat parait beaucoup plus raisonnable une fois que l’on a compris qu’il faut plutôt comparer 25*24/2 (le nombre de couples) à 1/365 : le produit est proche de 1.
Excellent article et bien vulgarisé, de surcroît! Bon anniversaire! 🙂
À noter que, lorsque N atteint K+1, on retrouve le principe des tiroirs (ou des pigeonniers) : http://fr.wikipedia.org/wiki/Principe_des_tiroirs 😉
Ainsi, pour les anniversaires, la 366e personne a (365-366+1)=0 choix pour que son anniversaire soit différent des 365 premières personnes, donc P=0, donc 1-P=1 : il y a *obligatoirement* 2 personnes avec le même anniversaire dans un groupe de 366 personnes ou plus (toujours dans le cas des années non bissextiles).
Reblogged this on Et_voici_le_bb…des_mots! (&my_words_are): and commented:
Il me semble bien que c’est un super site… et un gémeau de plus…
notre cas nous sommes 4, mon mari et mon fils sont né le même jour, ma fille et moi le même jour y à t’il un calcul ?
Pingback: Les bébés du nouvel an sont de plus en plus nombreux | Bokéhterie
Très simple finalement ! Je ne pensais pas qu’il y avait autant de chance dans un groupe de 50 personnes, impresionnant. Je vais essayer de calculer la probabilité qu’ils soient nés le même jour que moi, en comptant l’année bien entendu…
intéressant, néanmoins l’exemple ne prend pas en compte que la distribution des naissances n’est pas homogène sur une année. Avec la contraception, certaines femmes trouvent opportun de programmer la naissance de leur enfant pour cumuler congés estivaux
et maternité.
Il y a un pic de naissance début septembre aussi. On s’amuse bien lors des soirées du nouvel an.
Oui mais ca fait des prématurés.
Si la distribution est anormale alors la probabilité des collisions augmente encore !
Pingback: Actualités - Dossiers à lire | Pearltrees
jolie demonstration, j avais besoin de ça pour un travail à la fac
humm, petite question technique
pourquoi utilise-t-on la formule de l’arrangement simple / arrangement multiple, qui sous entend que l’ordre a de l’importance plutôt que les formules de combinaisons simples et multiples qui ne font pas intervenir l’ordre ?
En fait, l’ordre a de l’importance car, une fois choisi les N dates (parmi les 365 possibles) pour dénombrer toutes les situations, il faut distinguer (pour ces N dates) les différents cas où chaque personne est répartie dans ces N dates.
Juste choisir N dates (une combinaison, car on choisit N dates parmi 365) ne suffit pas à dénombrer les situations, car pour ces mêmes N dates, je peux avoir des gens répartis différemment.
Mais pour chaque choix de N dates, je sais que j’ai N! façons différentes de répartir N personnes dans ces N dates.
Donc si j’ai (N parmi 365) choix de N dates possibles, j’ai bien N!×(N parmi 365) possibilités de répartition de N personnes sur N dates choisies parmi les 365 possibles.
Exemple simple: je veux savoir combien de situations il y a pour que 3 personnes soient nées des jours différents de la semaine.
Je choisis donc 3 jours dans la semaine parmi les 7 (la combinaison).
Imaginons jeudi/vendredi/dimanche.
Mais on peut avoir: individi1 le jeudi, individu2 le vendredi et individu3 le dimanche…ou bien 2 le jeudi, 3 le vendredi et 1 le dimanche…etc…
Donc pour compter les situations, je dois voir combien de possibilités de répartition j’ai pour chaque choix de 3 jours (autrement dit, tenir compte de l’ordre)…Et il y en a 3!
Donc le résultat est bien (3 parmi 7)×3!, soit l’arrangement.
Pingback: Statistiques | Pearltrees
Un lieb vers une petite application avec DESMOS pour n et k quelconques
https://www.desmos.com/calculator/5umxvat57m
UN LIEN plus amusant DESMOS pour N et K quelconques
https://www.desmos.com/calculator/w7dxxzj7no
Pingback: Une probabilité peut en cacher une autre … | [Lab]map
un paquet de 52 cartes a environ 10^67 configurations possibles.
Est il probable qu’il y ait déjà eu 2 paquets mélangés exactement de la même façon dans l’histoire de l’humanité?
Non, c’est extrêmement peu probable. En utilisant la formule d’approximation utilisée dans l’article, il faudrait avoir eu plus de 10^34 mélanges fait par des êtres humains (on est a une proba de 0,46 environ). En supposant (généreusement) qu’un humain fait en moyenne dans sa vie 1000 mélanges différents de cartes, il faudrait qu’il ait existé 10^31 êtres humains jouant aux cartes….ce qui me paraît un tantinet exagéré 😛
Pingback: À VOIR | Pearltrees
Je suis un 23 novembre j’ai 2 cousines paternelles qui sont nées le 23 novembre un des fils de ma cousine le 23 novembre un fils à mon cousin le 23 novembre et le père de mes cousine est mort le 23 novembre. Probabilité. …
Passionant merci !
Pingback: Fakes, trilemme et loi des grands nombres – Enseigner au XXI siècle
Bonjour,
Pourquoi y a-t-il des points d’exclamations dans la formule ?
(Sinon, c’est le meilleur blog de vulgarisation de sciences)
C’est l’opération qu’on appelle « factorielle ». La factorielle de n, qu’on note n! signifie qu’on fait la multiplication de tous les entiers entre 1 et n.
La factorielle de 4 est le nombre 4!=1×2×3×4 😉
Et plus l’ensemble des choix est grand plus le résultat parait paradoxal :
Si on prend au hasard 1000 personnes nées dans les 1000 dernières années, la probabilité que 2 personnes soient nées exactement le même jour est proche de 75% !
Ce qui m’a donné envie de vérifier ça par l’informatique:
resultat : (pourcentage, elements dans le groupe)
[[0.3, 2], [0.8, 3], [1.0, 4], [2.4, 5], [4.3, 6], [5.6, 7], [8.2, 8], [9.1, 9], [13.0, 10], [15.3, 11], [17.2, 12], [17.7, 13], [22.8, 14], [25.5, 15], [27.2, 16], [31.1, 17], [31.8, 18], [39.1, 19], [38.5, 20], [44.9, 21], [46.8, 22], [51.6, 23], [52.5, 24], [55.7, 25], [60.1, 26], [60.7, 27], [65.2, 28], [68.0, 29], [70.5, 30], [71.9, 31], [75.7, 32], [79.2, 33], [78.6, 34], [82.5, 35], [83.9, 36], [85.5, 37], [86.5, 38], [88.7, 39], [89.9, 40], [89.7, 41], [91.4, 42], [91.1, 43], [93.9, 44], [92.7, 45], [93.0, 46], [95.9, 47], [96.6, 48], [96.0, 49], [96.9, 50], [96.6, 51], [98.2, 52], [97.6, 53], [98.1, 54], [97.9, 55], [99.2, 56], [99.2, 57], [99.4, 58], [99.5, 59], [99.4, 60], [99.6, 61], [99.2, 62], [99.8, 63], [99.5, 64], [99.8, 65], [99.7, 66], [99.7, 67], [99.8, 68], [99.8, 69], [99.8, 70], [99.9, 71], [99.7, 72], [99.8, 73], [99.7, 74], [99.9, 75], [99.9, 76], [99.9, 77], [99.9, 78], [99.9, 79]]
et pour aller plus loin, on a vu avec l’heure , pourquoi pas les minutes (24*60*365) , et on traduit en Français :
Dans un petit village de 860 habitants, il y a 50% de chance que deux personnes soit nés le même jour à la même minute