 Contrairement à ce qui est fréquemment supposé en science économique, l’être humain se comporte bien souvent de façon irrationnelle. De nombreuses expériences mettent en évidence notre irrationnalité, mais bien peu cherchent à expliquer son origine.
Contrairement à ce qui est fréquemment supposé en science économique, l’être humain se comporte bien souvent de façon irrationnelle. De nombreuses expériences mettent en évidence notre irrationnalité, mais bien peu cherchent à expliquer son origine.
Dans cette veine, des chercheurs de l’Université de Yale se sont demandés si notre irrationnalité humaine était de nature culturelle (et donc acquise), ou bien d’origine biologique (et donc innée). Pour tenter de répondre à cette question, ils ont analysé les choix économiques…d’une colonie de singes !
Et ces derniers se révèlent tout aussi faillibles que nous !
Monnaie de singe
Le Laboratoire de Cognition Comparée de Yale est spécialisé dans l’étude du comportement des singes capucins. Ces derniers sont des singes vivant en Amérique du Sud, et qui sont séparés de l’être humain par près de 35 millions d’années d’évolution. Afin de tester si ces singes pouvait comme nous se comporter de manière irrationnelle, K. Chen et ses collaborateurs ont organisé avec eux des expériences de nature économique.

Pour cela, ils ont d’abord introduit une monnaie, sous la forme de petits disques métalliques. Puis ils ont fait comprendre aux singes qu’ils pouvaient échanger avec les humains leurs disques contre de la nourriture, par exemple des morceaux de pommes.
Une fois que les singes eurent bien compris le principe de l’échange avec un seul expérimentateur humain, les chercheurs introduisirent des situations plus compliquées, faisant intervenir des choix entre deux expérimentateurs proposant des possibilités différentes (comme ci-contre), et dont certaines peuvent comporter une part de hasard, et donc de risque.
Un cas simple où les singes sont rationnels
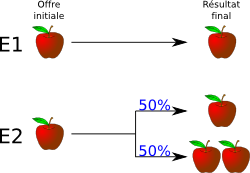 Dans une première expérience, on soumet les singes à la situation suivante. Ils ont la possibilité d’échanger une de leur pièce de monnaie avec deux expérimentateurs différents. Le premier expérimentateur (noté E1) propose un morceau de pomme, qu’il donne au singe si ce dernier choisit de faire l’échange. L’expérimentateur E2 propose également un morceau de pomme, mais si le singe choisit de faire la transaction, il lui offre un second morceau de pomme dans 50% des cas. Ce dilemme est résumé sur le diagramme ci-contre.
Dans une première expérience, on soumet les singes à la situation suivante. Ils ont la possibilité d’échanger une de leur pièce de monnaie avec deux expérimentateurs différents. Le premier expérimentateur (noté E1) propose un morceau de pomme, qu’il donne au singe si ce dernier choisit de faire l’échange. L’expérimentateur E2 propose également un morceau de pomme, mais si le singe choisit de faire la transaction, il lui offre un second morceau de pomme dans 50% des cas. Ce dilemme est résumé sur le diagramme ci-contre.
Bien entendu, pas besoin d’avoir fait Polytechnique pour s’apercevoir que l’expérimentateur E2 est plus intéressant ! Et les singes s’en rendent vite compte puisqu’une fois leurs choix stabilisés, ils finissent par préférer E2 dans près de 85% des cas.
Le singe irrationnel : la dépendance à la référence
Dans une seconde expérience, Keith Chen et son équipe [1] ont proposé à leurs capucins le choix représenté ci-contre :
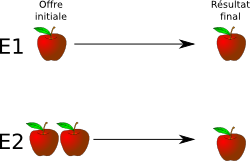
L’expérimentateur E1 propose un seul morceau de pomme, alors que E2 en affiche deux. Mais si le singe choisit E2, ce dernier retire un des deux morceaux et n’en donne qu’un seul. Au final, le hasard n’intervient pas, les deux choix sont strictement équivalents, mais la présentation est différente.
Si notre singe était rationnel, il choisirait indifféremment E1 ou E2, puisque le résultat est le même. Mais ce qu’on observe, c’est qu’il va choisir E1 dans 80% des cas ! On peut expliquer ce phénomène (qu’on retrouve aussi chez l’être humain) par la volonté qu’a le sujet d’éviter le sentiment de perte, provoqué par le fait de se voir retirer un des deux morceaux initialement promis.
C’est ce qu’on appelle la dépendance à la référence, car la manière dont on juge le résultat final (l’obtention d’un morceau de pomme) dépend de ce qu’on prend comme point de départ (l’affichage initial de 1 ou 2 morceaux suivant E1 ou E2). Il faut bien voir ce que ce résultat a de contre-intuitif le cas d’un animal, car choisir E1 oblige le singe a réfréner ses pulsions naturelles, qui le pousseraient à se jeter sur l’expérimentateur E2 qui affiche une quantité plus importante au départ.
La référence à la dépendance est un cas d’irrationnalité, car elle nous conduit à faire une différence de traitement entre deux situations pourtant identiques, mais présentées différemment. Mais il y a pire : ce phénomène peut nous conduire à carrément modifier nos choix pour des simples questions de présentation. Voyons en un exemple chez l’humain, avec ce qu’on appelle l’effet de renversement.
L’effet de renversement
En 1981, D. Kahneman et A. Tversky ont publié un papier dans Science [2] présentant une expérience troublante. Imaginez que vous soyez soumis au choix suivant :
Une épidémie touche une population de 600 personnes, et vous avez le choix entre deux traitements possibles, notés A et B. Voici ce que l’on sait de ces traitements :
- si vous choisissez le traitement A, 200 personnes seront sauvées avec certitude ;
- si vous choisissez le traitement B, il y a une probabilité 1/3 que 600 personnes soient sauvés, et une probabilité 2/3 que personne ne soit sauvé.
Je vous laisse faire votre choix.
Maintenant, considérez la situation suivante :
Au cours d’une épidémie similaire, 600 personnes sont malades et on vous propose de choisir entre les traitements C et D.
- Si vous choisissez le traitement C, 400 personnes mourront avec certitude;
- Si vous choisissez le traitement D, il y a une probabilité 1/3 que personne ne meure et une probabilité 2/3 pour que 600 personnes meurent.
Si l’on présente les deux situations précédentes à un grand nombre de personnes, environ 3/4 des gens préfèrent le traitement A au traitement B, et environ 3/4 préfèrent le traitement D au traitement C.
Et pourtant si vous relisez bien les questions, A et C sont strictement identiques, tout comme B et D ! Dans ces deux dilemmes, ce n’est que la présentation qui change, et donc le point de référence que l’on prend pour faire notre choix. Et cela suffit à nous faire modifier nos décisions. Perturbant, non ?
Cet effet appelé est « effet de renversement ». Il vient du fait que quand on raisonne sur des gains (des personnes sauvées), on préfère l’option certaine plutôt que l’option aléatoire, mais quand on raisonne sur des pertes (des gens vont mourir), on est préfère prendre l’option aléatoire (et donc risquée) pour conserver une petite chance de s’en tirer sans rien perdre.
Cet effet est fréquemment observé chez les investisseurs (et les propriétaires immobiliers) qui refusent de vendre à perte, et préfèrent prendre le risque de conserver leurs actions (ou leur maison), dans l’espoir même faible que sa valeur remonte.
L’effet de renversement chez les singes capucins
Comme vous avez pu le deviner, les chercheurs de Yale ont voulu tester si les singes capucins étaient eux aussi soumis à l’effet de renversement. Ils leur ont proposé le choix entre une situation certaine et une situation risquée, mais dans l’expérience 1 on présente les choses sous forme d’un gain, et dans l’expérience 2 sous forme d’une perte. Voici le schéma des deux expériences proposées aux singes :
Et là ça n’a pas raté [3] : le singe est tout aussi irrationnel que nous. Les deux expériences 1 et 2 sont absolument identiques au final, mais quand on présente les choses comme un gain (Exp.1), le singe choisit préférentiellement l’option certaine (E1) alors que quand on les présente comme une perte (Exp.2), il choisit l’option risquée (E2).
L’homme vaut-il mieux que le singe ?
Les travaux de l’équipe de Yale permettent donc de penser qu’une partie de l’irrationnalité dont nous faisons tous preuve dans nos comportements quotidiens n’est pas nécessairement quelque chose d’acquis ou de culturel, mais est peut être profondément ancré en nous depuis plusieurs millions d’années d’évolution.
Parmi les autres observations intéressantes qui ont été faite dans ces expériences, les auteurs rapportent que tout comme l’homme, le singe capucin est susceptible de voler de l’argent à ses semblables. En revanche, ils n’ont jamais observé de situation où le singe semble économiser son pécule.
Enfin dernier exemple étonnant, K. Chen rapporte [4] qu’il a même pu observer un singe donnant un de ses disques en métal à un autre en échange de faveurs sexuelles, constituant peut être le premier cas non-humain de prostitution !
Des billets reliés, ici ou ailleurs :
Le paradoxe de Monty Hall chez le pigeon
Irrationnalité animale, sur le Webinet des Curiosités.
Références :
Le laboratoire de cognition comparée de l’Université de Yale
[1] Chen, M. K., Lakshminaryanan, V. & Santos, L. R. (2006). The evolution of our preferences: Evidence from capuchin monkey trading behavior. Journal of Political Economy, 114(3). 517-537
[2] Amos Tversky; Daniel Kahneman, The Framing of Decisions and the Psychology of Choice, Science, Vol. 211, No. 4481. (1981), pp. 453-458.
[3] Lakshminarayanan, V., Chen, M. K., & Santos, L. R. (2011). The evolution of decision-making under risk: Framing effects in monkey risk preferences. Journal of Experimental Social Psychology. In Press.
[4] Monkey Business, New York Times, 5 juin 2005
Images :
Photo du singe et des expérimentateurs : extrait du TED Talk de Laurie Santos
Photo du capuçin : A. Chapman
Schémas : Science Etonnante





22 Comments
Moi je sais pas choisir entre A et B… c’est grave?
Espèce d’irrationnel, va !
En fait je crois me souvenir que quand on fait l’expérience du choix A/B avec une certaine somme d’argent plutôt qu’avec des vies humaines, on constate que pour de petites sommes, les gens sont plutôt joueurs, et pour de grosses sommes, ils font le choix qui élimine l’incertitude. D’où des théories sur la forme de la fonction d’utilité (on suppose que le choix est rationnelle mais que ce ne sont pas les gains que l’on optimise, mais leur utilité)…
Bon, c’est bien joli, mais comment choisir de façon rationnelle entre A et B quand l’enjeu est celui que tu décris? Je n’en ai pas la moindre idée. C’est cornélien!
En fait ça va plus loin que la simple prise en compte de l’utilité. Quand on prend juste en compte l’utilité, on trouve en effet que de manière générale, les gens préfèrent le choix déterministe au choix aléatoire, même à espérance identique, car l’utilité de 200€ est inférieure à deux fois l’utilité de 100€ (c’est l’aversion au risque que je raconte là)
Mais dans des théories plus fines, on va plus loin que la simple prise en compte de l’utilité, en ajoutant aussi des effets de déformation de la perception des probabilités. Les gens ont tendance à surestimer les probabilités faibles de gagner et sous-estimer les probabilités importantes de perdre je crois.
Finalement si on a un jeu qui permet de gagner S1 avec une probabilité x et S2 avec une probabilité 1-x, ce que les gens vont chercher à maximiser ça n’est pas l’espérance du gain x.S1 + (1-x).S2 mais f(x)u(S1)+f(x)u(S2) où u() désigne l’utilité et f(.) la fonction de déformation de la perception des probabilités. Une fonction telle que f(0)=0 et f(1)=1, mais qui au milieu n’est pas linéaire mais plutôt concave pour les gains et convexe pour les pertes (si je me souviens bien).
On ne maximise pas l’espérance du gain, mais l’espérance « déformée » de l’utilité du gain.
A et C ne sont pas strictement identiques. Enfin, ça dépend de la lecture qu’on en fait. Mais personnellement, je lis :
A) vivants >= 200
C) morts >= 400 –> vivants <= 200.
Tu as raison, il y a une ambiguïté que je n’ai pas levée. Dans le papier original, c’est plus clair :
Assume that the exact scientific estimate of the consequences of the programs are as follows:
=> If Program A is adopted, 200 people will be saved
etc.
Ces expériences sont fascinantes, merci pour ce billet. En particulier je ne connaissais pas celle du renversement des préférences. Est-ce que ça marche aussi sur d’autres animaux non primates? Car je me demande si la dépendance à la référence peut-être liée à la conscience de soi…
Concernant la forme de la courbe d’utilité, une explication simple est que l’on est sensible au logarithme des récompenses (ou des pertes), tout comme le reste de notre système sensoriel (le bruit, les fréquences musicales, la douleur, le poids, la luminosité etc. c’est la loi de Weber). C’est ce qui expliquerait en particulier nos comportements très irrationnels envers tout ce qui est gratuit (puisque Log(0) est infini…)
Pour des expériences sur les autres animaux, il y a ce papier sur les étourneaux, qui semble montrer une tendance au risque pour les pertes mais plutôt neutre pour les gains.
http://users.ox.ac.uk/~kgroup/publications/pdf/marsh_kacelnik_2002_pnas_framing.pdf
Je n’ai pas lu le papier mais j’ai l’impression que je devrais 🙂
Ils mentionnent dans l’abstract un truc étrange : les animaux seraient averses au risque pour les quantités de bouffe, mais prendraient des risques pour réduire le temps d’attente !
Pingback: >L’amour du risque | Le Webinet des Curiosités
Pingback: L’expérience de Asch sur le conformisme | Science étonnante
Pingback: sciences | Pearltrees
Pingback: Un singe ferait-il mieux que votre conseiller financier ? | Science étonnante
Pingback: Les animaux se reconnaissent-ils dans un miroir ? | Science étonnante
Pingback: Le singe, un homo économicus irrationnel...
Pingback: Experience bébé/singes | Pearltrees
Pingback: Bebe singe | Pearltrees
Pingback: Maman singe | Pearltrees
Superbe article et félicitations pour ce blog. Toutefois, quelque chose me chagrine.
Dans l’expérience de 1981 (et en fait dans les suivantes aussi). le choix du traitement A (200 personnes seront sauvées avec certitude) contre le traitement B (il y a une probabilité 1/3 que 600 personnes soient sauvés, et une probabilité 2/3 que personne ne soit sauvé) n’est pas équivalent. Il ne l’est que sur le long terme (l’espérance de gain « nombre de personne sauvé » si je ne prend que le traitement B tend vers 200 en vertu de la loi des grands nombres).
Mais sur une seul expérience, le résultat est fort différent!!! Supposons que le singe choisissent soit A soit B avec 50%. On a donc 50% de sauver 200 personnes, 25% de sauver 0 personnes et 25% de sauver 600 personnes => moyenne=250 personnes.
Sur une seul experience, si maintenant on a 75% de chance de choisir le traitement A. On a donc 75% de sauver 200 personnes, 17.5% de sauver 0 personnes et 17.5% de sauver 600 personnes => moyenne=150+52.5=202.5!! personnes.
Pingback: Méfiez-vous d’un juge affamé ! | Science étonnante
J’avais choisi A pour le premier cas, et C pour le second cas, mais ai été surpris par le commentaire qui les suivait.
Autant j’ai senti que les options B et D sont équivalentes, autant les options A et C ne m’ont pas semblé équivalentes, parce que leur formulation m’apparait ambigüe d’après le commentaire qui en est fait.
Pour A, j’avais compris que non‑pas exactement 200 personnes exactement seront sauvées, mais que 200 personnes sûrement seront sauvées et peut‑être plus. De même, pour C, je n’avais pas compris que 400 personnes exactement mourront, mais que 400 personne sûrement mourront et peut‑être plus.
La formulation est ambigüe …
Même si j’ai choisi les options équivalentes dans les deux cas, le second cas m’a donné le sentiment d’être un choix plus difficile à faire.
Merci pour l’article, il m’a beaucoup intéressé (je m’intéresse à l’origine animale des comportements humains et à la sémantique, et là c’est du deux en un).
Pingback: Ya2n | Pearltrees
Intéressant, après en effet il faudrait distinguer entre logique formelle et verbal. Car souvent c’est le langage qui est source d’ambiguïté.