La vidéo du jour traite d’un sujet que j’avais évoqué dans mes articles précédents sur les codes secrets, et sur la machine à inventer des mots : la méthode « MCMC » qui permet de déchiffrer avec une excellente efficacité à peu près n’importe quel message chiffré par substitution. https://www.youtube.com/watch?v=z4tkHuWZbRA Pour cette vidéo, je me suis surtout basé sur l’article introductif de Perci Diaconis Diaconis, P. (2009). The markov chain monte carlo revolution. Bulletin of the American…
Vous connaissez le canapé Söft ? La commode Utrad ? L’étagère Hång ? L’armoire Muskydd ? Le mixeur Skymfor ? La poële Kukväde ? Le placard Klöstig ? Le circuit Rundering ? La table Oljulstad ? Les rideaux Lykofåtsly ? Le bureau Håkmanedfol ? La chaise Sjärganskig ?
Eh bien contrairement aux apparences, ces noms ne font pas partie du véritable catalogue Ikea ! Ils ont été fabriqués automatiquement par un algorithme qui s’inspire de vrais mots suédois pour en créer de nouveaux, qui « sonnent suédois » mais n’existent pas dans cette langue.
Pour la première fois, j’ai décidé de vous proposer une vidéo non pas sur un sujet scientifique bien établi, mais sur un petit projet de recherche personnel que j’ai entrepris : comment créer des mots nouveaux qui sonnent bien ?
http://www.youtube.com/watch?v=YsR7r2378j0
Pour ceux qui voudraient en savoir plus sur la méthode utilisée, voici quelques explications supplémentaires.
Ma vidéo du week-end traite des codes secrets et de la cryptographie RSA. Si j’en crois les chiffres, ça passionne plus les foules que la biologie cellulaire d’il y a deux semaines !
http://www.youtube.com/watch?v=8BM9LPDjOw0
Un sujet connexe que j’ai hésité à aborder dans la vidéo concerne les techniques de décryptage par Markov Chain Monte Carlo (MCMC pour les intimes) que j’ai un peu découvertes en lisant un excellent papier intitulé The Markov Chain Monte Carlo revolution (P. Diaconis, Bulletin of the American Mathematical Society 46.2 (2009): 179-205.). Les MCMC sont des algorithmes assez génériques aujourd’hui utilisés un peu partout de la physique statistique jusqu’aux problèmes de génétique des populations ou de linguistique (par exemple mon billet sur l’origine des langues indo-européennes)
La nouvelle a fait grand bruit parmi les chercheurs : d’après un statisticien américain, il se pourrait que presque 25% des résultats publiés dans littérature scientifique soient tout simplement faux.
Voilà qui ne va pas aider la science, déjà pas mal discréditée aux yeux d’une partie de nos concitoyens. Mais qu’est-ce que cette nouvelle veut dire ?
Pour le comprendre, il faut se pencher sur la méthode scientifique que les chercheurs utilisent pour valider leurs résultats, celle qui leur permet de décider si oui ou non ils ont vraiment trouvé quelque chose.
L’affaire est entendue : c’est la fin du monde dans quelques jours. Alors un grand merci à tous mes fidèles lecteurs qui m’auront suivi jusque là !
Et pour finir en beauté, nous allons bien sur parler de l’Apocalypse ! Mais comme il s’agit de sciences, nous allons discuter de la probabilité prochaine de la fin du monde.
Et vous allez voir que ça n’est pas si catastrophique que vous le pensez, mais c’est plus inquiétant que vous ne le croyez !
Préliminaire : Ce billet est la suite de celui de la semaine dernière, qui portait sur les probabilités conditionnelles et introduisait la formule de Bayes. Si ces notions vous sont familières, vous n’êtes pas obligés d’aller le lire. Dans le cas contraire, n’hésitez pas à vous rafraîchir la mémoire !
La semaine dernière, je vous ai présenté la célèbre règle de Bayes, qui permet de relier la probabilité conditionnelle de « A sachant B » à celle de « B sachant A »
$latex P(A | B) = \frac{P(B | A) P(A)}{P(B)}&s=2&fg=0000ff$
Nous avions vu un cas simple, où A et B désignaient respectivement le fait d’être rouge et carré pour un objet que l’on tire au hasard dans une urne (« quelle est la probabilité qu’il soit carré sachant qu’il est rouge »), ainsi qu’un cas plus subtil où il était question de dépistage du cancer.
L’idée était de souligner la différence entre « la probabilité d’avoir le cancer sachant qu’on est dépisté positif », notée P(C | +), et « la probabilité d’être dépisté positif sachant qu’on a le cancer », notée P(+ | C). D’après la formule de Bayes, on peut relier les deux par :
$latex P(C | +) = \frac{P(+ | C) P(C)}{P(+)}$
Aujourd’hui, nous allons voir en quoi la formule de Bayes peut s’interpréter dans un contexte plus général, et devenir un outil formidable pour quantifier la manière dont nous raisonnons, et même dont notre cerveau fonctionne !
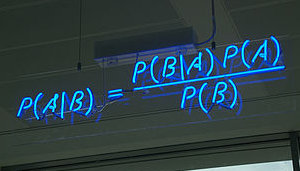Vous venez de passer un test pour le dépistage du cancer. Le médecin vous convoque pour vous annoncer le résultat : mauvaise nouvelle, il est positif. Pas de chance, alors que ce type de cancer ne touche que 0.1% de la population.
Vous demandez alors au praticien si le test est fiable. Sa réponse est sans appel : « Si vous avez le cancer, le test sera positif dans 90% des cas ; alors que si vous ne l’avez pas, il sera négatif dans 97% des cas ». L’affaire paraît entendue…
Et pourtant, à votre avis, après le résultat d’un tel test, quelle est la probabilité que vous ayez le cancer ? 90% ? 87% ? Moins que ça ?
Pour répondre à cette question, il va falloir faire un tout petit peu de probabilités…mais ça en vaut la peine, vous allez découvrir que malgré votre test positif, la probabilité d’être malade n’est que de 2.9% ! Creusons un peu ce petit paradoxe, et partons à la découverte de la formule de Bayes, l’une des plus importantes de toute l’histoire des sciences !
Hier soir, vous avez organisé une petite fête et invité une vingtaine d’amis. Alors qu’au milieu de la soirée, la conversation tourne (allez savoir pourquoi) sur les signes du zodiaque, deux de vos invités découvrent avec stupeur que leur anniversaire tombe le même jour !
– Incroyable !
– Ah oui, quelle coïncidence !
– Tu imagines la probabilité que ça arrive ?
Eh bien justement, parlons en de la probabilité !
Le problème de Monty Hall est un célèbre jeu de probabilités qui tire son nom d’une émission télévisée. On le qualifie de paradoxe, car la bonne stratégie à adopter nous semble souvent contre-intuitive.
Des expériences montrent d’ailleurs que même en répétant plusieurs fois le jeu, l’être humain a vraiment du mal à comprendre le truc, alors que le pigeon, lui, s’en sort très bien.
De là à conclure à la supériorité intellectuelle des volatiles, il n’y a qu’un pas !
Le paradoxe de Monty Hall trouve son origine dans le jeu télévisé Let’s Make a Deal, diffusé aux Etats-Unis à partir de 1963. L’animateur Monty Hall y proposait le choix suivant.
Un candidat est présenté face à 3 portes : derrière une seule de ces portes se trouve un cadeau, alors que derrière chacune des deux autres portes se trouve un objet sans intérêt (typiquement : une chèvre).
Que doit faire le candidat ? Conserver ou changer ?
Réfléchissez donc 5 minutes…