David Louapre – Page 18 – Science étonnante

Vie du blog 17 novembre 2014

Qu’est-ce qu’un brevet ?

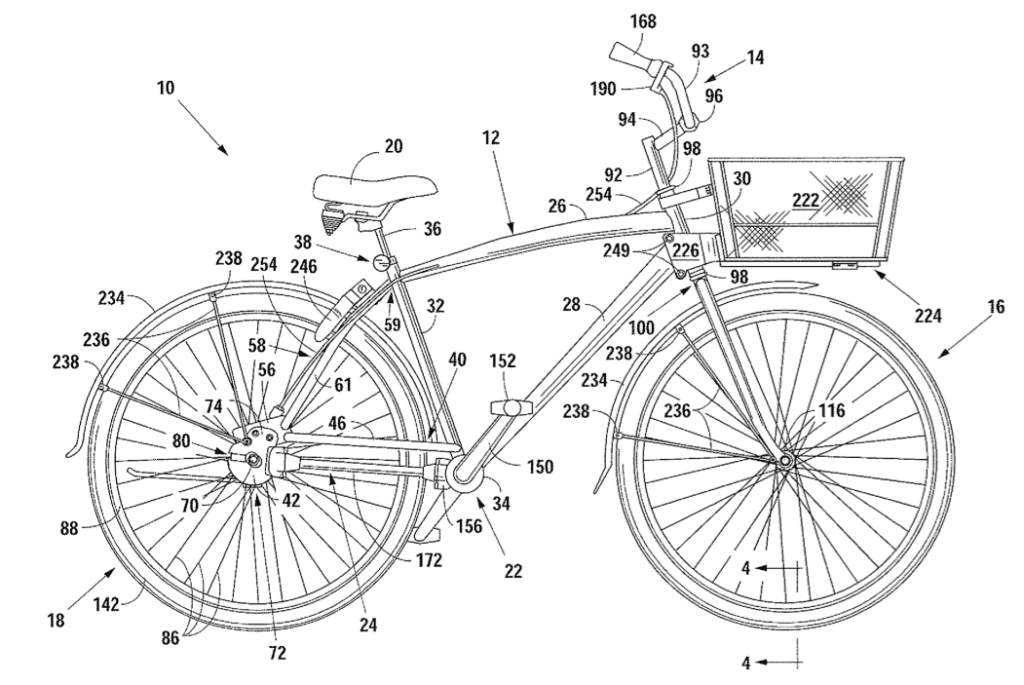Les brevets sont partout autour de nous. Qu’il s’agisse de la super dernière technologie de rasoir 9 lames, de l’évaluation des efforts de recherche des entreprises, de la guerre Apple-Samsung ou des débats de société sur la brevetabilité du vivant : on entend tout le temps parler de brevets !

Et pourtant, tout le monde n’a pas forcément une idée très claire de ce qu’est vraiment un brevet; c’était d’ailleurs mon cas avant que je commence à travailler dans la recherche appliquée. Mais après 10 ans passés à lire beaucoup de brevets et à en déposer quelques uns, je me suis dit que ça valait le coup de faire un petit billet là-dessus.

Biologie 10 novembre 2014

Pourquoi y-a-t-il des gauchers ?

Bien que le chiffre exact ne soit pas si simple à déterminer, on estime que l’espèce humaine compte environ 10% de gauchers, pour 90% de droitiers…auxquels il faut bien sûr ajouter environ 1% d’ambidextres (oui, je sais, ça fait 101%).

Conséquence de tout ça : nous vivons dans un monde irrémédiablement fait pour les droitiers, comme en témoigne cette tasse avec l’anse à droite.

Seul un humain sur 10 est gaucher, donc : mais pourquoi une telle (dis-)proportion ? Si notre préférence manuelle était totalement le fruit du hasard, on s’attendrait plutôt à 50/50. Ou à l’opposé, ça n’aurait pas été surprenant qu’elle eut été la même pour tout le monde : tous droitiers, ou tous gauchers. Après tout nous avons tous le coeur à gauche et le foie à droite !

Mais 10% de gauchers, pourquoi ?

Physique 3 novembre 2014

La houppe de Haidinger

Vous avez déjà certainement entendu parler de ces animaux qui voient moins bien les couleurs que nous. Nos amis les chiens ne voient pas le rouge et l’orange; quant aux dauphins, ils sont carrément monochromes ! Mais d’autres animaux perçoivent au contraire plus de couleurs que nous. Certains insectes sont même capables de détecter la polarisation de la lumière !

Vous ne savez pas exactement ce qu’est la polarisation de la lumière ? C’est bien normal, puisque nous autres humains, nous sommes incapables de la voir ! Quoique…

A la fin de ce billet, vous vous apercevrez peut-être que vous possédez cette super-capacité inutile : voir la lumière polarisée. Tout ça grâce à la houppe de Haidinger.

Biologie 27 octobre 2014

Pando : Le plus gros et le plus vieil être vivant du monde ?

Aujourd’hui, je voudrais vous parler d’un individu étrange que certains n’hésitent pas à considérer comme le plus gros et le plus vieil être encore vivant sur Terre. Non, je ne vous parle pas d’un humain, ni même d’un improbable animal.

C’est tout simplement un arbre.

Ou plutôt des arbres.

Enfin non, UN arbre.

Mathématiques 20 octobre 2014

La première conjecture de Hardy-Littlewood

La semaine dernière, je vous ai parlé de ce qu’on appelle la deuxième conjecture de Hardy-Littlewood, qui affirme qu’il y a toujours plus de nombres premiers entre 0 et N que dans tout autre intervalle de longueur N.

Cette conjecture a de quoi intriguer, car on n’en a jamais trouvé un seul contre-exemple, et pourtant les spécialistes sont convaincus qu’elle est fausse. Mais ils estiment que pour trouver un contre-exemple, il faut aller chercher au-delà de $latex 10^{174}$ !

Aujourd’hui, nous allons voir ce qui permet de faire cette estimation. Il s’agit d’une autre conjecture proposée au même moment par les mêmes mathématiciens : celle qu’on appelle la première conjecture de Hardy-Littlewood.

Mathématiques 13 octobre 2014

La deuxième conjecture de Hardy-Littlewood

C’est l’histoire d’un physicien à qui on demande d’étudier la conjecture

« Tout nombre impair est un nombre premier. »

Il commence donc à regarder les nombres impairs les uns après les autres :

1 : ok. 3 : ok. 5 : ok. 7 : ok. 9 : …hum. 11 : ok.

13 : ok. 15 : …euh. 17 : ok. 19 : ok.

Et le physicien finit par conclure :

« La conjecture est vraie; …en première approximation. »

Au-delà du fait que cette conjecture est évidemment carrément fausse, cette histoire illustre le fait qu’en mathématiques il n’y a pas de demi-mesure : soit une conjecture est vraie pour ABSOLUMENT TOUS les nombres, soit elle est fausse ! Un seul contre-exemple suffit pour démolir l’édifice.

Et pourtant aujourd’hui nous allons parler d’une conjecture un peu étrange : la deuxième conjecture de Hardy-Littlewood. Personne n’en a jamais trouvé de contre-exemple, et malgré cela les spécialistes sont convaincus qu’elle est fausse ! Mais le premier contre-exemple est attendu fabuleusement loin, au point qu’on estime que la conjecture est vraie jusqu’à au moins 10 puissance 174 !

Mathématiques 6 octobre 2014

Le nombre d’Erdös-Bacon-Sabbath

Parmi les petits jeux auxquels s’adonnent les mathématiciens dans leur temps libre, il y a calculer leur nombre d’Erdös.

Ce nombre mesure la distance qui les sépare du célèbre mathématicien hongrois Paul Erdös du point de vue des collaborations scientifiques.

La règle du jeu est simple :

si vous êtes Paul Erdös, votre nombre d’Erdös est 0;
si vous avez écrit un article scientifique avec Erdös, votre nombre est 1;
si vous avez écrit un article scientifique avec quelqu’un dont le nombre est 1, votre nombre est 2;
et ainsi de suite…

Biologie 29 septembre 2014

L’optogénétique : contrôler le cerveau avec de la lumière

Notre cerveau est sans nul doute la machine la plus complexe qui soit. Il faut dire que chez nous les humains, on y trouve pas loin de 100 milliards de neurones, reliés entre eux par près d’un million de milliards de connexions.

Pas étonnant que l’on ait du mal à comprendre comment fonctionne ce satané cerveau !

Et pourtant depuis une dizaine d’années, une technique nouvelle est apparue, qui est peut-être en passe de révolutionner les neurosciences : l’optogénétique.

Vie du blog 22 septembre 2014

La cérémonie IgNobel 2014

C’est l’évènement que tout le monde attend chaque fois avec impatience ! Depuis de nombreuses années, la remise de ces prix est devenu le point d’orgue de l’année scientifique, et tout le monde rêve d’en avoir un. Je ne veux pas parler des prix Nobel, mais bien sûr de leurs doubles maléfiques : les prix IgNobel !

Décernés au mois de septembre, ils récompensent « la science improbable, celle qui fait d’abord rire puis ensuite réfléchir ».

C’est jeudi qu’a eu lieu à l’université de Harvard la cérémonie au cours de laquelle les prix sont annoncés et remis aux heureux élus, en général des mains de véritables prix Nobel. Comme j’habite dans le coin, je me suis dit que cette année il ne fallait pas laisser passer ça. Les tickets d’entrée sont partis comme des petits pains, mais j’étais bien préparé. !

Physique 15 septembre 2014

Pourquoi est-il impossible de se sortir d’un trou noir ? (2/2)

La semaine dernière, je vous ai montré (dans ce billet) comment on pouvait appréhender la notion de trou noir rien qu’en utilisant des concepts de physique de lycée; notamment qu’on pouvait voir un trou noir comme un astre dont la vitesse de libération est supérieure à celle de la lumière.

Et pourtant cette façon de voir les choses ne résiste pas à une analyse plus poussée. En effet, tant qu’on considère la gravité comme une simple force, on peut toujours imaginer arriver à la contrer en prenant un moteur suffisamment puissant qui délivrerait une force encore supérieure. Donc dans la théorie de la gravité de Newton, il n’est pas vraiment possible d’avoir des trous noirs.

Pour comprendre pourquoi même la plus puissante des fusées ne pourrait pas se sortir d’un trou noir, il faut abandonner l’idée que la gravité est une force normale. Et pour cela il va falloir mettre un peu les mains dans le cambouis, et traiter le problème avec les outils de la théorie de la relativité générale d’Einstein.