 La semaine dernière, je vous ai proposé une vidéo d’introduction à la mécanique quantique. Comme on peut s’en douter avec ce genre de sujet, pas mal de commentaires ont été faits et beaucoup de questions ont été soulevées, et les réponses ne se trouvaient pas toujours dans la vidéo ou dans le billet qui l’accompagnait.
La semaine dernière, je vous ai proposé une vidéo d’introduction à la mécanique quantique. Comme on peut s’en douter avec ce genre de sujet, pas mal de commentaires ont été faits et beaucoup de questions ont été soulevées, et les réponses ne se trouvaient pas toujours dans la vidéo ou dans le billet qui l’accompagnait.
Je voudrais aujourd’hui revenir sur un point particulier : l’analogie que j’ai faite entre le principe d’incertitude d’Heisenberg et le rapport entre la durée et la fréquence d’un son. Cette image n’a pas convaincu tout le monde, alors je vais la détailler un peu, et essayer de vous persuader qu’elle est en fait bien mieux qu’une analogie : il s’agit pour ainsi dire du même phénomène que le principe d’incertitude de Heisenberg !
Le spectre d’un son
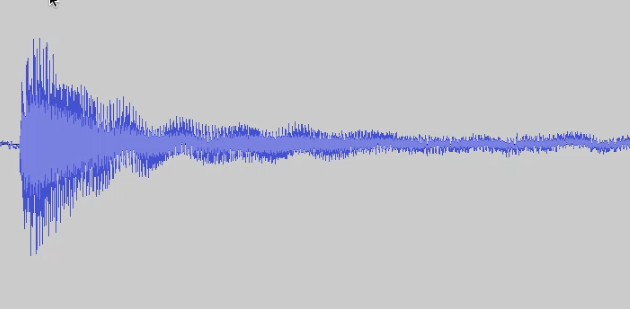
Considérons ce qu’on visualise généralement quand on enregistre un son : l’intensité du signal sonore en fonction du temps. Ci-dessous vous voyez un exemple d’un signal enregistré (un des sons de ma guitare que j’utilise dans la vidéo).
On va noter \(x(t)\) cette intensité en fonction du temps. (Dans un enregistrement numérique, ce signal \(x(t)\) n’est pas une fonction continue du temps, puisque le son est échantillonné à une certaine fréquence, par exemple 44 000 Hz. Mais en pratique si la fréquence d’échantillonnage est suffisamment élevée, on peut faire comme si le signal était continu.)
Quand on a un signal de ce genre, on peut considérer sa décomposition en fréquences, c’est-à-dire essayer de le représenter comme une somme de sinusoïdes. Mathématiquement pour faire cette décomposition on effectue une opération appelée transformée de Fourier.
Le coefficient de Fourier associé à la fréquence \(f\) pour le signal \(x(t)\) se calcule par
\(\displaystyle X(f) = \int dt\ x(t) e^{2i\pi f x}\)
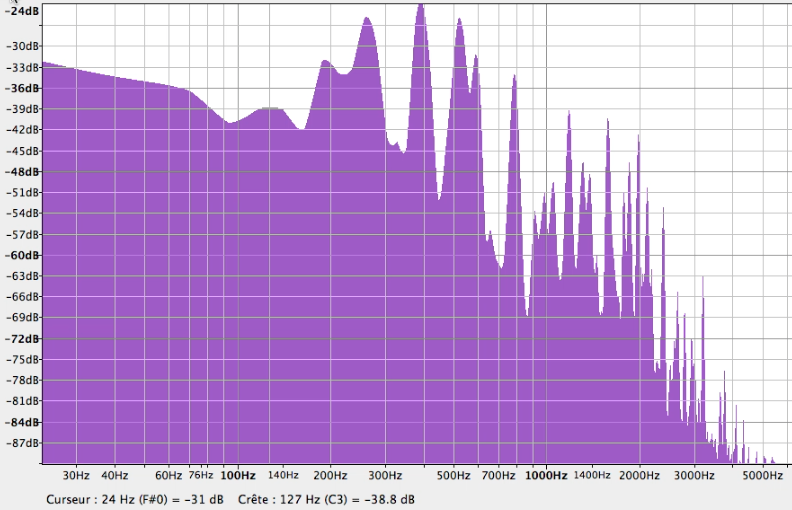
En représentant la norme de \(X(f)\) en fonction de f, on obtient l’intensité de chacune des fréquences de la décomposition, ce qu’on appelle parfois le spectre du signal. Dans ma vidéo, j’ai montré rapidement comment faire l’opération avec Audacity, un logiciel de traitement du son qui permet notamment d’analyser et de tracer rapidement le spectre d’un enregistrement sonore.
Le spectre d’un signal court
Ce que j’expliquais dans la vidéo, c’est que la durée d’un signal et l’étalement de son spectre sont liés par une relation analogue à celle du principe d’incertitude. Cette relation implique qu’il est impossible d’avoir un son qui soit à la fois très court et possédant un spectre très pur. Nous allons voir numériquement et mathématiquement pourquoi c’est vrai, et en quoi ça a à voir avec Heisenberg.
Pour s’en convaincre, on va faire tout ça proprement en générant nous même un signal et en faisant la transformée de Fourier (pour ceux que ça intéresse, j’ai fait ça en Python.)
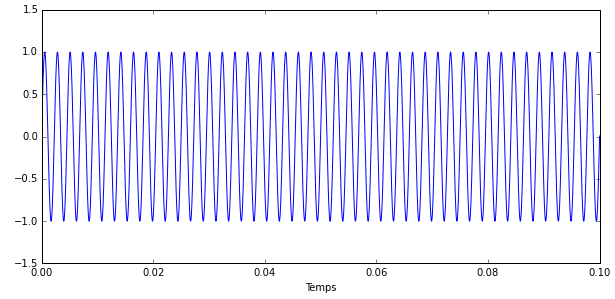
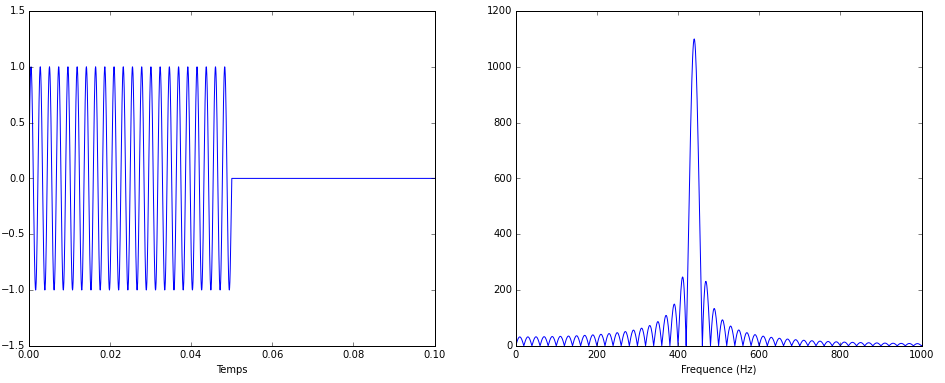
Considérons un signal échantillonné à 44 000 Hz et composé d’une sinusoïde pure de fréquence 440 Hz, le fameux « La » qui sert de référence aux musiciens.
Je vous ai représenté ci-dessus 0,1 seconde d’un tel signal et vous pouvez compter 44 périodes d’oscillations sur le graphique.
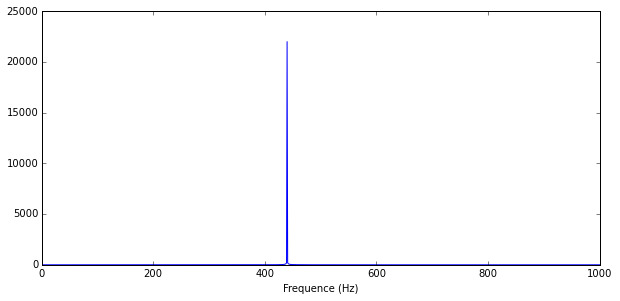
Considérons une seconde entière de ce signal (elle contient donc 440 périodes de la sinusoïde), calculons sa transformée de Fourier et traçons le spectre associé.
Vous voyez que c’est zéro partout et qu’il y a un pic parfait à 440 Hz. Logique, non ? C’est la fréquence de notre sinusoïde !
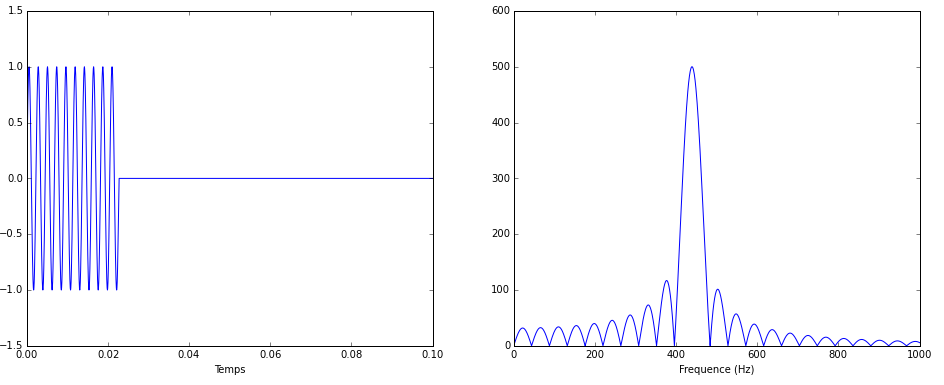
Très bien. Maintenant raccourcissons la durée du signal, de sorte qu’il ne fasse que 0,05 secondes, et ne contienne donc que 22 périodes. Voici le signal et le spectre que l’on obtient :
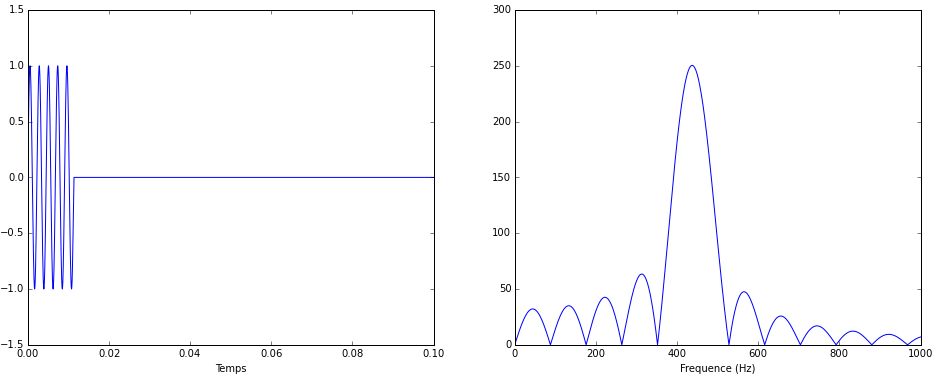
Vous remarquez quelque chose ? On voit des fréquences parasites apparaître, à un niveau heureusement assez faible. Poussons le bouchon avec un signal ne contenant que 10 périodes
Puis 5 périodes
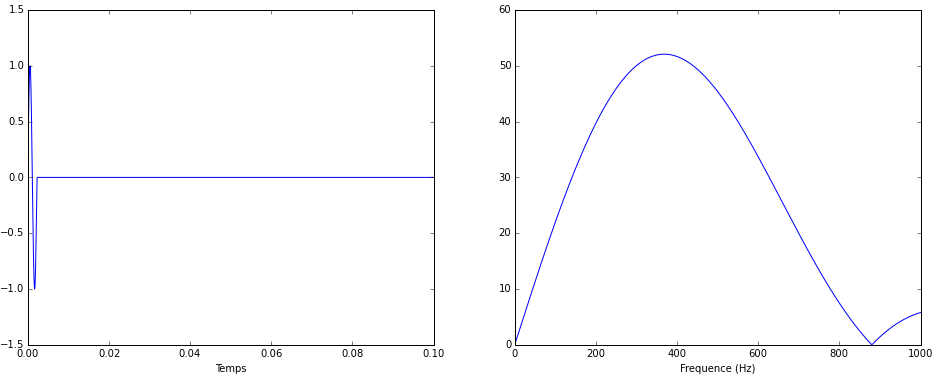
Et carrément une seule période :
Vous voyez le phénomène ? Plus on raccourcit la durée du signal sinusoïdal, plus des fréquences parasites viennent s’ajouter et produire au final un spectre bien plus étalé que le pur « 440Hz » que l’on attendait.
La justification mathématique
Ce phénomène d’étalement du spectre n’est pas un artefact numérique lié à l’algorithme qui fait la transformée de Fourier, c’est une réalité mathématique : plus un signal est court, plus sa largeur spectrale est importante. Et ce même quand on a un signal que l’on imagine être « pur » en fréquence.
Je voudrais donner plusieurs arguments pour expliquer ce phénomène : un argument plutôt physique, un argument numérique et un argument franchement théorique.
Sur l’aspect physique des choses, souvenez vous qu’un spectre représente une décomposition du signal sonore. En particulier il est possible de reconstruire le son d’origine en superposant des sinusoïdes pures dont les coefficients sont donnés par la transformée de Fourier (c’est la transformée de Fourier inverse).
Il est du coup facile d’imaginer qu’un signal sinusoïdal infiniment long et un signal sinusoïdal fini ne peuvent pas avoir le même spectre, puisqu’en faisant l’opération de transformée de Fourier inverse on doit retomber sur le signal d’origine. Si la sinusoïde infiniment longue a un spectre pur ne contenant qu’une fréquence, alors la sinusoïde « finie » doit forcément contenir d’autres fréquences. Physiquement on peut comprendre que ces fréquences supplémentaires sont nécessaires car pour passer de la zone de 0 à une sinusoïde, puis revenir à 0, il faut introduire des fréquences supplémentaires, et ce d’autant plus que la durée de la sinusoïde est courte.
Un argument un peu plus numérique mais qui dit la même chose, plutôt pour ceux qui connaissent un peu la transformée de Fourier. Un résultat très important c’est que la transformée de Fourier d’un produit de 2 signaux est égale à la convolution des transformées de Fourier de ces signaux. Or une sinusoïde de durée finie peut-être vue comme le produit d’une sinusoïde infinie et d’une fonction « porte » qui vaut 1 là où la sinusoïde est allumée, et 0 là où elle est éteinte.
La transformée de Fourier de la sinusoïde finie va donc nécessairement contenir par convolution la transformée de Fourier de la porte, et c’est celle-là même qui provoque l’étalement du spectre.
(Petite digression : cet effet de porte peut justement être assez gênant quand vous voulez analyser le spectre d’un signal fini…ce qui souvent est le cas en pratique ! C’est pour ça que lorsqu’on traite un signal on essaye de le multiplier par une fonction qui va croître puis décroitre d’une manière plus douce que la porte brutale, et ce afin de minimiser les fréquences parasites. On parle de fonction « fenêtre » et il en existe tout un tas, mais par définition aucune ne peut être parfaite. D’ailleurs si vous faites de l’analyse de spectre avec Audacity, il est vraissemblable qu’il intègre déjà ce genre de correction.)
Un théorème mathématique !
Dernier argument purement théorique, on peut démontrer une forme mathématiquement précise et générique de cette idée que l’étalement temporel d’un signal et son étalement spectral ne peuvent pas être simultanément aussi petits que l’on veut.
Ce théorème dit que
\(\displaystyle V(x)V(X) \geq \frac{1}{16}\pi^2\)
où \(V(x)\) représente la variance du signal et \(V(X)\) la variance de sa transformée de Fourier, définies comme
\(\displaystyle V(x) = \int dt\ t^2 x(t)\)
\(\displaystyle V(X) = \int df\ f^2 X(f)\)
(ici on suppose un signal centré sur zéro mais le résultat reste même si ça n’est pas le cas).
Bref j’espère vous avoir convaincu que ce que je raconte dans la vidéo est absolument correct : la durée et la largeur spectrale d’un son ne peuvent pas être simultanément aussi petites que l’on veut, leur produit est borné inférieurement d’une manière qui rappelle furieusement Heisenberg.
Ce que nous dit ce résultat, c’est que LA fréquence d’un son et LE moment où il se produit ne sont pas des concepts parfaitement déterminés.
Notez bien que ce théorème est totalement générique : prenez une fonction mathématique, prenez sa transformée de Fourier : il existe une inégalité qui dit que plus l’une est localisée, moins l’autre peut l’être.
Pourquoi Heisenberg c’est ça ?
Le lien avec la mécanique quantique c’est que c’est exactement ce qui s’y passe pour l’onde de probabilité en position et l’onde de probabilité en impulsion. Elles sont la transformée de Fourier l’une de l’autre !
Si \(\Psi(x)\) est l’amplitude de probabilité en position, alors \(\Phi(p)\) l’amplitude de probabilité en impulsion vaut
\(\displaystyle \Phi(p) = \int\ dx \Psi(x) e^{ipx/\hbar}.\)
Dans cette relation, l’impulsion \(p\) joue le rôle de fréquence spatiale pour l’onde de probabilité.
La probabilité en position et celle en impulsion étant transformées de Fourier l’une de l’autre, il existe entre ces deux fonctions la même inégalité que ce qu’on a vu précédemment : plus notre particule est localisée en position, moins elle l’est en impulsion, et réciproquement !
Et précision importante, comme dans le cas du son, il s’agit bien d’une relation d’indétermination : il n’y a pas de sens à parler de LA position et de LA fréquence d’une une onde de probabilité. Ces concepts ne sont pas parfaitement déterminés simultanément.
Evidemment sur le plan expérimental, cette indétermination va se traduire par ce qui ressemble à une incertitude : si je prends plein de particules décrites toutes par le même état (la même fonction d’onde) et que je les mesure plein de fois, je vais observer une dispersion en position et en vitesse. Mais cette dispersion n’est pas de nature expérimentale mais bien fondamentale, c’est une indétermination et pas une incertitude.
Apparemment la petite histoire c’est qu’Heisenberg dans son article original avait utilisé le mot allemand pour indétermination (« Ungenauigkeit »), mais avait aussi employé une fois le mot pour incertitude (« Unsicherheit »). Quand le concept a été traduit et popularisé, c’est malheureusement celui-ci qui a été retenu…même s’il est finalement un peu inapproprié !
Voilà j’espère que tout cela vous aide à bien comprendre ce principe d’incertitude/indétermination, qui n’est en fin de compte pas si mystérieux car tout à fait naturel dans le cas du son.



28 Comments
Belle illustration! Dans cette histoire de spectre, on peut faire aussi le parallèle avec la diffraction d’une lumière monochromatique par une fente: la répartition de l’intensité lumineuse dans le plan d’observation est un sinus cardinal, le même que celui qu’on obtient pour le spectre sonore en créant un obstacle « temporel » pour le son. Une autre façon de relier deux domaines différents.
Et au niveau sonore? On « entend » les fréquences supplémentaires ou bien le son est trop court pour s’en rendre compte ?
VOIR MON BLOG: fermaton.overblog.com sur la CONSCIENCE HUMAINE.
Super article ! Je comprends mieux la comparaison maintenant merci d’avoir détaillé =)
J’apprécie également l’explication concernant « indétermination » et « incertitude » j’ai vu une conférence d’Etienne Klein où il expliquait ce que tu dis dans ton article, et c’est vrai que c’est fou à quel point le choix des bons mots est important dans la compréhension et à quel point aussi cet aspect n’est absolument pas respecté dans les médias où « l’à peu près » est Maitre…
Quand j’entends encore que « Le Big Bang est l’origine de l’Univers » à la télé j’ai envie de la jeter par la fenêtre =p
Pingback: Actualités - Dossiers à lire | Pearltrees
Salut David,
juste un petit commentaire sur les enregistrements : en acoustique on enregistre l’amplitude du signal en fonction du temps et pas son énergie ! Le reste de ton billet est très bien et ton blog toujours aussi agréable à suivre.
Ah oui je crois que j’ai dit « intensité », qui doit être le carré de l’amplitude c’est ça ?
Content de te voir toujours par ici 🙂
3 commentaires :
Tout d’abord, faisant suite à une remarque précédente, en acoustique on mesure la pression et non pas intensité. L’intensité acoustique est une grandeur vectorielle définie comme le produit de la pression par la vitesse : I = pv.
Une erreur plus grossière (du point de vue d’un nerd du traitement du signal) est de négliger l’échantillonnage ainsi que tous les artefacts dus au traitement numérique des signaux. Si on n’observe pas de lobes secondaires sur le premier signal, c’est que la transformée de Fourier qu’effectue un ordinateur est une transformée de Fourier discrète dont la formule est différente de la transformée de Fourier continue. En particulier, elle effectue une sommation sur le nombre d’échantillons dont est constitué le signal. Et un signal est nécessairement de durée finie. Les lobes secondaires dans les figures suivantes sont dus au zero-padding qui a été appliqué sur le signal et pas du tout au principe d’incertitude de Heisenberg. Si l’on tronque le signal et que l’on effectue une TF à 2200 échantillons, on n’aura pas de lobes secondaires. De la même manière, si l’on prend une seconde de signal et que l’on fait une transformée de Fourier à 88000 échantillons en complétant le signal avec des zéros (le fameux zero-padding), on verra apparaître les lobes. Je ne prétendrais pas que c’est simple, mais en gros la transformée de Fourier discrète considère que le signal discret est périodique, donc on n’a pas besoin d’utiliser de fonction porte si l’on effectue une TFD d’exactement le support du signal. Pour être rigoureux, il faut donc préciser les transformations spectrales effectuées, et ce au détriment de la simplicité et la concision de l’exemple.
Cependant, le principe d’incertitude de Heisenberg est effectivement présent dans le traitement des signaux sous la forme purement mathématique énoncée en fin d’article. On le retrouve principalement en analyse temps-fréquence, discipline initiée par les travaux de Gabor dans les années 40 qui valent à l’inégalité le surnom de Heisenberg-Gabor. Une formulation simple est de dire que le plan temps-fréquence n’admet pas de pavage arbitrairement petit. (De plus, le pavage optimal est obtenu en prenant une gaussienne.) Comme le dit l’article, c’est mathématiquement exactement la même propriété de la transformée de Fourier qui est à l’origine des deux principes.
En conclusion, l’échantillonnage est toujours important en traitement du signal, mais on a bien affaire à un truc de science étonnante !
Bonjour et merci pour le commentaire éclairé !
J’ai quand même du mal à me convaincre que l’effet du zero-padding ne soit pas formellement la même chose que Gabor/Heisenberg.
Est-ce que tu veux dire que les lobes qu’on voit ne sont pas le sinus cardinal qui est la TF de la fonction rectangle ? (je n’ai pas vérifié que çà collait)
Je vois 4 échelles échelles de temps dans la question :
* la longueur totale du signal T1
* la durée T2 sur laquelle le signal est non nul
* la période T3 de l’échantillonnage
J’ai envie de penser que si T1 >> T2 >> T3, faire la DFT est une excellente approximation de la TF qu’on pourrait faire analytiquement (et qui nous donne donc le sinus cardinal)
Mais je crois qu’il faut que je refasse quelques calculs et simus pour en être totalement convaincu !
Guillaume pense que tronquer un signal infini permet d’obtenir la même transformée qu’avec le signal infini *en général*. C’est faux dès qu’on a autre chose qu’une sinusoïde pure, car la disparition des lobes parasites est un *artefact* venant d’une situation particulière choisie et sans intérêt : signal comportant une seule fréquence et fréquence d’échantillonnage adaptée à la fréquence du signal (qui doit donc être connue a priori).
Bonjour,
félicitation pour la qualité des articles, et des vidéos.
Je pousserai juste une analogie supplémentaire au principe d’incertitude, elle aussi sur la base du traitement des signaux numériques.
Une mauvaise fréquence d’échantillonnage conduit à un repliement de spectre (théorème de Shannon), qui nuit à la détermination du signal => il n’est plus reconstituable, il y a incertitude. (mais encore faut-il s’en rendre compte !)
Ce phénomène est particulièrement rencontré pour les signaux très dynamiques (tiens tiens) et lorsqu’on arrive en limite technologique de nos outils de mesure (je n’imagine toutefois pas que ce soit le cas lorsqu’on s’attelle à caractériser une particule … quoique 😉
Pingback: Le principe d’incertitude de Heisenberg a...
Merci pour ce blog de qualité. C’est vraiment très bien fait, j’apprends des choses de manière très intuitive. L’écriture.
En ce qui concerne les aspects mécanique quantique, que je connais assez bien…
L’analogie est intéressante mais à ses limites dont la principale est l’interprétation physique.
Si la durée et la fréquence d’un son sont corrélés en raison d’une relation physique intrinsèque entre les deux, le principe d’Heisenberg ne dit pas du tout la même chose.
Le fait que deux observables soient incompatibles exprime le fait que les deux grandeurs physique qu’on essaie de mesurer au niveau microscopique, par analogie avec notre monde macro, n’ont pas de sens pris ensemble et renvoie donc à la question de la nature des choses. Ceci est vrai pour toutes les formulations de l’inégalité, temps/énergie ou position/impulsion.
En ce qui concerne cette dernière, cela veut tout simplement dire que les corpuscles, au sens de la mécanique classique, n’existent pas, et par conséquent essayer de mesurer ces deux grandeurs physiques simultanément n’a pas de sens.
Cela se voit très bien dans l’expérience des fentes de Young que vous citez au sens où la localisation spatiale d’un électron n’a pas de sens tant qu’on n’essaie pas de la mesurer. D’ailleurs en ce qui concerne les superpositions d’état, on ne sait pas vraiment ce que veut dire A + B. Il me semble que dire « à la fois A et B » est un raccourci de langage dont on a tous du mal à se défaire, mais il me semble que la notion sous jacente du « à la fois » peut être dangereuse et fausse dans le sens où elle entendrait une sorte d’ubiquité pour la position par exemple, alors qu’on sait que la théorie quantique est non locale, ce qui est un peu plus complexe et contre intuitif.
Ceci dit, encore un grand merci.
interessante ton analogie, bien que je prefere incertitude, car fondamentalement, ces particules sont la, c’est la mesure qui n’est pas parfaite. ou comme dit on la mesure affecte leurs etats
Ce n’est pas une analogie, c’est le phénomène physique le plus fondamental. Ce n’est donc pas une incertitude venant de l’appareil de mesure. Fondamentalement cela veut dire que le zéro mathématique (et donc l’infini) n’existe pas en physique. L’univers entier est né de cela. Le zéro physique s’exprime dans un dipôle oscillant stochastique en….donnant un choix parmi une infinité d’impulsions possibles. Ce qui est infini ici, ce n’est pas la quantité physique « impulsion » mais seulement la largeur du spectre des probabilités des impulsions possibles (la dispersion). Là où beaucoup d’erreurs sont commises, c’est la non prise en compte d’un dipôle où les deux impulsions (symétriques et réelles dans le référentiel confiné de chacune des branches), s’annulent strictement dans le référentiel de ce dipôle. Autrement dit Heisenberg (versus dipôle), détermine le zéro physique stochastique à partir duquel l’univers est né…. à partir de rien. La loi de Heisenberg (versus monopôle) dit que le vide possède une énergie de point zéro. C’est vrai mais il ne dit pas que c’est dans ce vide (déjà construit) qu’est fournit l’énergie minimale. Tout le monde aura compris que l’univers n’est pas né de son propre vide (plein d’énergie) mais né d’un vide physiquement, vraiment vide. Le strict rien physique est prolifique et c’est pour cela que nous pouvons en discuter ici sur ce site intéressant.
Très intéressant! Merci pour ces explications.
Une petite coquille s’est glissée dans la première formule: le x dans l’exponentielle doit être remplacé par un t.
Très bonne idée d’utiliser de concert les supports vidéo et écrit. Je trouve qu’ils se complètent bien.
La vidéo plus accessible et captivante et l’écrit pour les précisions et les petits détails !
En pratique, en traitement du signal, on utilise la transformée de Fourier rapide (le FFT des oscillos et logiciels)
https://fr.wikipedia.org/wiki/Transformation_de_Fourier_rapide
Et le fenêtrage le plus courant est celui de Hamming :
https://fr.wikipedia.org/wiki/Fen%C3%AAtrage
Voilà ^^
Petite erreur dans la première formule (x au lieu de t dans l’exponentielle)! Le placement des dt ou dx est aussi un peu curieux dans cette formule et les autres.
Cela n’enlève en rien l’intérêt de ce texte: bravo pour cette analogie que je vois pour la première fois.
Top ton billet David, j’avais jamais vu cette illustration, c’est lumineux!
Bonjour, félicitations pour votre noble effort de pédagogie !
Je crois comprendre l’analogie et je pense que l’idée générale est correcte, mais pour être parfaitement convaincant il faudrait aménager l’explication. En effet la sinusoide tronquée n’est pas un signal périodique et on ne ferait donc jamais une simple transformée de Fourier sur le signal complet: on ferait une analyse de Fourier (avec filtre anti-aliasing comme vous l’indiquez) sur des sous-échantillons avec un certain overlap entre eux. Le spectre serait alors différent selon l’instant considéré. J’ai le sentiment à la lecture du billet que vous savez déjà cela, mais de fait la démonstration / l’analogie manque de me convaincre complètement à cause de cet élément. Pour être franc, j’ai envie de vous croire (émotion/intuition), mais votre démonstration ne me convainc pas (maths). Ce point rejoint, je pense, ce que Guillaume a essayé d’expliquer.
Je profite de l’occasion pour commenter un commentaire: c’est bien l’amplitude (quantité complexe et non réelle) qu’on étudierait en acoustique car la phase a de l’importance… mais lorsque vous ferez votre spectre vous abandonnerez la notion de phase: avec mes sous-écantillons qui s’overlappent, cela revient à dire que les événements (acoustiques) à un instant sont indépendants des événements à l’instant suivant (et c’est bien le cas physiquement). Pour chaque sous-échantillon il n’y a plus de notion de phase, et faire le spectre de P ou celui de P^2 ne change rien d’autre que la dynamique du spectre (ie, l’échelle en ordonnée) (surtout si on met les quantités en dB c’est-à-dire en échelle Log). Cela signifie que parler d’énergie ou d’amplitude ne change pas la validité de votre démonstration (qu’elle soit bonne ou mauvaise).
Bon … Je doute que tout ceci soit d’une clarté exemplaire mais si vous le désirez vous pouvez feuilleter un cours d’acoustique, ou un bouquin marrant qui vient de sortir ‘Des chiffres et des notes’ de Migeot, vous y trouverez des explications plus claires si vous le désirez.
Je ne me permettrai pas de commenter la partie quantique de la démonstration 🙂
Bravo encore pour ce billet
Je n’arrive pas à comprendre la raison de ce phénomène, est-il dû à l’amortissement de la vibration générant le son, comme quoi une oscillation ne peut pas être arrêtée à l’instant ? Et si oui, pourquoi cette indétermination dont vous parlez n’arrive qu’en phase d’arrêt mais aussi en phase de démarrage ?
Marco
Merci, votre remarque sur ce principe d’incertitude s’appliquant à toute autre fonction me laisse penser qu’à partir du moment où il y a de l’énergie, l’ensemble des états de tout système quelqu’il soit possède cette indetermination intrinsèquement .
Je viens de découvrir votre blog et il me semble très intéressant pour rendre plus accessible les questions mettant en jeu des principes physiques.
1. problème de la largeur du pic fréquentiel
S’agissant de vos explications ainsi que celles de certains des commentateurs sur l’impact de la durée d’observation, de l’influence du zero-padding, j’ai l’impression qu’il y a quelques confusions.
Pour une sinusoïde pure de durée infinie, on retrouverait peu ou prou le même spectre pour un signal numérique avec une raie unique si on disposait d’un nombre très conséquent d’échantillons (et donc de périodes). Par contre, quand on limite la durée de l’observation, on n’accède pas au signal initial « infini » s[n] mais à un autre signal correspondant à la multiplication de ce signal « infini » s[n] par une porte rectangulaire w[n] où seuls les échantillons du signal situés à l’intérieur de la porte sont pris en compte pour le calcul du spectre, on travaille alors avec le signal s_2[n]=w[n].s[n].
Or, la multiplication fréquentielle de signaux temporels a pour transformée la convolution des transformées des
signaux temporels. On passe donc de s_2[n]=w[n].s[n] à S_2[f]=W[f]*S[f] où f peut désigner une fréquence continue comme une fréquence discrète selon la version numérique de la transformée de Fourier que l’on utilise.
D’un point de vue pratique, cela signifie que chacune des fréquences présentes dans le spectre S[f], correspondant à un pic fin unique, va donner lieu à une réplique du spectre W[f] de la fenêtre qui va « interférer » avec les autres répliques par sommation complexe… Et, si deux répliques sont trop proches, elles vont conduire à des soucis de séparation et/ou de masquages complexes que même l’utilisation du zéro-padding ne permettra pas de résoudre : chaque spectre W[f] a potentiellement un lobe central et on ne peut séparer deux fréquences distantes de moins d’un demi-lobe central. En fait, l’utilisation du zéro-padding conduit de manière implicite à augmenter le nombre de fréquences (points) pour le spectre et donc à mieux dessiner sa courbe.
Maintenant, la fenêtre rectangulaire a pour spectre un sinus cardinal dont le lobe central a une largeur fréquentielle inversement proportionnelle à la longueur temporelle, donc plus la fenêtre est courte et plus le lobe central de notre sinus cardinal sera large, ce qui explique vos différents tracés en fonction de la durée d’observation de la sinusoïde.
Pour limiter l’impact des lobes secondaires correspondant au spectre en sinus cardinal de la fenêtre rectangulaire, qui sont de plus susceptibles de masquer ou modifier les pics centraux dans le cas où le signal comporte d’autres fréquences, on utilise des fenêtres de pondération (qui remplacent donc w[n] pour le calcul de s_2[n]) qui tentent d’atténuer ces lobes secondaires voire de les faire quasiment disparaître pour certaines. Mais au fur et à mesure que les lobes secondaires sont atténués, on introduit un élargissement du lobe central jusqu’à, par exemple, aboutir au cas de la fenêtre gaussienne dont le spectre est aussi une gaussienne.
Il faut alors augmenter la longueur temporelle de la fenêtre, au besoin avec le zéro-padding, pour faire diminuer la largeur du lobe central.
Ainsi, sous Audacity par exemple, on a intérêt à tester pour des signaux simples (sinus pure, deux sinusoïdes de fréquences très proches, deux sinusoïdes de fréquences moins proches, …) ce que donnent les différentes fenêtres d’analyse proposées en partant de la meilleure résolution fréquentielle (utilisation d’une taille de 65536 voire 32768) afin de choisir une fenêtre qui « nous parle » et diminuer ensuite sa taille jusqu’à la valeur pour laquelle on commence à avoir des difficultés à interpréter le spectre calculé.
2. le lien avec les « incertitudes »
L’analogie proposée avec le son est pertinente tant que l’on reste dans le cadre d’une analyse du signal avec la transformée de Fourier qui correspond à une approximation (dans le cas numérique) du signal sur une base d’exponentielles complexes donc de signaux périodiques. Il existe d’autres analyses et il conviendrait de discuter de ce principe d' »incertitude » pour celles-ci…
En fait, on pourrait probablement proposer qu’il s’agit d’incertitudes de Fourier vu que l’inégalité sur le produit des incertitudes de localisations temporelle et fréquentielle est directement liée à la construction des transformées de Fourier, une conséquence en fait de leur définition.
De ce point de vue, le principe d’incertitudes est une propriété de la transformée de Fourier de dimension 1 et ce quelle que soit la nature des signaux et des paramètres étudiés (temps ou coordonnée spatiale, fréquence ou pulsation temporelle ou spatiale).
Mais, il me semble que cette propriété n’est plus utilisable dès lors que l’on a un signal qui dépend d’au moins deux variables ou tout du moins que l’on est alors bien en peine (sauf cas très particuliers pas à peu intéressants en pratique ?) de séparer les incertitudes de localisation spatio-temporelles comme fréquentielles (k et \omega dans le cas de signaux dépendant de r et t).
Et, c’est là que j’ai des doutes concernant le principe d’incertitude (ou les inégalités) d’Heisenberg…
En effet, alors que l’on part de phénomènes spatio-temporels « unidimensionnels » (donc de dimension 2 !), on construit des formules pour les paquets d’ondes qui font apparaître des spectres soit purement fréquentiellement « spatiaux » (donc ne dépendant que de la pulsation spatiale k) soit des spectres purement fréquentiellement « temporels » (donc ne dépendant que de la fréquence f ou de la pulsation temporelle \omega) en considérant que l’on a affaire à une superposition d’ondes chromatiques.
Or, si l’on considère la description fréquentielle de signaux « unidimensionnels » quelconques \psi(r,t), on aboutit à une description par des bi-transformées de Fourier spatio-temporelles \Psi(k,\omega) si on travaille avec les pulsations temporelles et spatiales. Et, si on introduit en plus l’hypothèse que les phénomènes sont ondulatoires, on fait bien apparaître des ondes monochromatiques « classiques » mais affectés de poids fréquentiels qui restent des bi-transformées de Fourier spatio-temporelles, qui correspondent aux valeurs de \Psi(k, \omega) le long de la droite \omega + k.c_0= 0. Soit une restriction du plan complexe (k,\omega) à la droite \omega + k.c_0= 0.
En partant ainsi du cas général « unidimensionnel », on aboutit alors à des définitions des paquets d’ondes qui font intervenir sous l’intégrale une bi-transformée de Fourier et interdisent, pour moi, l’utilisation de l’inégalité classique conduisant aux inégalités d’Heisenberg. Et, même en se plaçant dans des cas instationnaires ou au temps t=0, on ne change pas le fait que ce n’est pas une transformée de Fourier 1D (temporelle ou spatiale) mais une transformée de Fourier 2D (spatio-temporelle) qui figure sous l’intégrale, contrairement à ce que l’on écrit en construisant les paquets d’ondes à partir du cas très particuliers des ondes monochromatiques.
Et c’est encore pire dans le cas « tridimensionnel » car c’est alors une quadri-transformée de Fourier qui apparaît sous l’intégrale.
De plus, il me semble que passer par la démonstration quantique pour des opérateurs qui ne commutent pas ne permet pas de « sauver » le principe d’incertitude d’Heisenberg car derrière les matrices se cache une projection dans une base d’exponentielles complexes analogue à celle utilisée pour construire la transformée de Fourier spatio-temporelle.
En résumé, on pourrait proposer que :
– le principe d’incertitude existe quand on s’intéresse à l’analyse de signaux purement 1D (temporels ou spatiaux) dès que l’on utilise une transformée de Fourier (cas de l’analyse de Fourier de signaux purement temporels ou spatiaux) ;
– le principe d’incertitude d’Heisenberg n’est a priori pas utilisable en l’état si on considère des signaux au minimum 2D (spatio-temporels par exemple) donc en Mécanique Quantique ;
– il faudrait étudier ce que donne la question des incertitudes de localisations spatio-temporelle et fréquentielles afin de voir si (ou quand ?) on peut séparer le produits des quatre incertitudes « spatiales » et « temporelles » et retomber sur des inégalités séparées temps/pulsation temporelle et espace/pulsation spatiale pour les localisations spatiales et temporelles correspondant aux inégalités classiques.
Juste une précision (!) linguistique:
en Allemand « indétermination » se dit « Unbestimmtheit » (et c’est bien ce mot qu’a utilise Heisenberg, d’après E. Klein). Ungenauigkeit veut dire imprécision.
Commentaire général: je trouve les vidéos et le blog vraiment didactiques et précises. Je suis fan. Un grand merci!
« c’est une réalité mathématique : plus un signal est court, plus sa largeur spectrale est importante. »
C’est un peu comme « plus une information est vague, plus elle décrit l’ensemble d’une réalité ».
« c’est une indétermination et pas une incertitude. »
Tout comme l’information vague dont je parle.
Finalement si on place le Principe d’incertitude d’Heisenberg dans l’histoire de l’évolution de l’univers; il est la simple expression du fait que l’univers à ses débuts avait beaucoup plus de choix « viables » (ou d’équilibre) que plus tard dans son histoire. Car plus l’information augmentait de pertinence (plus il y avait de réussites viables ou équilibrantes d’expérimentées), plus l’incertitude diminuait. À un point tel que finalement, l’incertitude d’Heisenberg disparut de la réalité universelle chez le proton qui est stable et l’atome de fer qui l’est également. Le Principe d’incertitude d’Heisenberg est un manque de détermination dans l’événement lui-même (donc fondamental) et non dans la donnée.
Enfin c’est ce qui me semble.
Si l’on considère chaque grandeur d’une particule comme une dimension dans l’espace des mesurandes, la mesure approximative d’une de ces grandeurs revient à une projection de cette particule sur l’espace des mesurandes ; ce qui de facto comme toute projection réduit la précision sur les autres dimensions.
Par analogie, en cartographie on utilise différents systèmes de projection du 3D sur 2D. Certains comme Mercator conservent les angles, d’autres comme Peters les surfaces, d’autres plus ou moins les distances. Mais il est impossible de disposer avec précision deux de ces grandeurs : toute projection choisie favorise la précision sur l’une des grandeurs au détriment des autres.
Cette comparaison vaut ce qu’elle vaut, elle est essentiellement analogique, mais peut-être assez parlante pour le néophyte.
Pourquoi il y a pas des références bibliographiques ou c’est moi qui sais pas chercher sur le site?
Cordialement,
Petit détail: je crois que la relation entre les variances est …>=1/(16*Pi^2) au lieu de >= Pi^2 / 16
Bonjour à tous
Pour info, la page anglaise de Wikipedia confirme le bien-fondé des arguments de David :
« Il est depuis devenu plus clair, cependant, que le principe d’incertitude est inhérent aux propriétés de tous les systèmes ondulatoires , [11] et qu’il apparaît dans la mécanique quantique simplement en raison de la nature ondulatoire de tous les objets quantiques. »
https://en.wikipedia.org/wiki/Uncertainty_principle#