Quelle est la différence entre une clepsydre et un sablier ?

« La clespydre, Roger ! La clepsydre !…Sors !… Sors, bordel ! »

Voilà qui sans nul doute évoquera de bons souvenirs aux fans de l’émission « Les clés de Fort Boyard ». Je crois d’ailleurs avoir découvert le mot « clepsydre » à cette occasion.

Alors la clepsydre est-elle un simple sablier avec de l’eau ? Eh bien non ! Il s’avère qu’il est beaucoup plus facile de mesurer le temps avec du sable qu’avec de l’eau, et pourtant la physique de l’écoulement du sable est affreusement complexe !

Comprendre comment coule le sable paraît futile, mais c’est en réalité un sujet d’importance capitale en géophysique et dans certains procédés industriels. La physique des « écoulements granulaires » est justement un domaine dans lequel plusieurs équipes françaises ont fait des avancées importantes ces dernières années.

Une affaire de débit

Les clepsydres existent depuis l’antiquité, et sont un des moyens les plus simples de mesurer l’écoulement du temps. Vous n’avez même pas besoin d’une forme de sablier : deux bassines et un trou feront l’affaire, comme sur la reconstitution ci-contre d’une clépsydre athénienne.

Et pourtant il y a un problème avec la clepsydre : quand la moitié de l’eau est tombée, c’est moins de la moitié du temps qui s’est écoulé !

En effet dans une clepsydre la vitesse d’écoulement varie avec la hauteur de l’eau restante : le débit n’est donc pas constant, plus rapide au début, plus lent à la fin.

Heureusement le sablier a amélioré tout ça ! Introduit en Europe au cours du moyen-âge, les marins se sont vite rendus compte que le sablier était plus stable que la clepsydre, et que sa vitesse d’écoulement constante le rendait plus pratique pour mesurer les durées intermédiaires.

Mais alors, quelle différence entre le sable et l’eau ?

Le débit d’une clepsydre : la loi de Torricelli

Pour se convaincre que la vitesse d’écoulement dépend de la hauteur d’eau, on peut faire une manip simple : prendre une grande bouteille d’eau, y percer 3 trous à 3 hauteurs différentes, et observer ! Vous devriez constater que le jet est d’autant plus puissant que le trou est bas dans la colonne.

Au XVIIe siècle, le physicien italien Evangelista Torricelli avait noté cette dépendance, et calculé la variation de débit avec la hauteur d’eau. Sous sa forme moderne, la loi de Torricelli nous dit que pour un trou de rayon R, et une hauteur d’eau h le débit est égal à

\(D = \sqrt{2gh}\ \ \pi R^2\)

où g est bien sûr l’accélération de la pesanteur. Une autre manière de voir cette loi, c’est simplement de dire que la vitesse de l’eau en sortie est égale à \(\sqrt{2gh}\).

Pour s’en souvenir c’est très simple, c’est la vitesse d’une goutte d’eau en chute libre : l’eau qui sort de la colonne d’eau possède la vitesse qu’elle aurait si elle tombait du haut de la colonne.

Une troisième manière de voir la loi de Toricelli, c’est de remarquer que la pression au bas de la colonne est proportionnelle à la hauteur, et donc que la vitesse est proportionnelle à \(\sqrt{P}\). La vitesse augmente donc avec la pression en bas de la colonne, cela paraît bien normal !

Le débit d’un sablier : la loi de Beverloo

La situation pour le sablier est à la fois plus simple et plus compliquée : plus simple car la hauteur de sable ne joue pas sur la vitesse, plus compliquée car on ne dispose pas d’une loi aussi simple que celle de Toricelli.

Et pourtant il existe un moyen simple de trouver la bonne loi : faire de l’analyse dimensionnelle, c’est-à-dire regarder simplement les unités des quantités que l’on a et que l’on veut obtenir. Si la hauteur d’eau n’intervient pas, il ne nous reste plus grand chose pour fabriquer une formule : la gravité g (unité : m/s2) et le rayon R (unité : m) du trou. Pour fabriquer un débit (unité : m3/s), on doit forcément avoir quelque chose proportionnel à la quantité

\(\sqrt{g} R^{5/2} = \sqrt{gR}\ \ R^{2}\)

C’est ce qu’on appelle la loi de Beverloo. Il existe un moyen très simple de comprendre cette loi : il suffit de regarder la formule la plus à droite ci-dessus où j’ai simplement séparé \(R^2\) et \(\sqrt{R}\) : la loi de Beverloo est similaire à celle de Toricelli, sauf que la hauteur totale h a été remplacée par le rayon R du trou.

Tout se passe comme si la vitesse d’écoulement du sable était celle d’une colonne de sable de hauteur R, qu’elle que soit la « vraie » hauteur de sable. Une autre manière de l’interpréter, c’est de dire que si on ajoute du sable en haut, la pression en bas n’augmente pas !

La théorie des arches

Pour comprendre d’où vient la loi de Beverloo, on peut utiliser une observation que l’on retrouve souvent dans les écoulements granulaires : les arches. On sait que du sable dans un cylindre ne se comporte pas comme de l’eau. Si on ajoute du sable supplémentaire en haut de la colonne, son poids ne sera pas supporté par le bas de la colonne (comme avec de l’eau) mais pas les grains intermédiaires qui frottent contre les parois.

Cette friction permet notamment la formation d’arches, c’est-à-dire de structures ressemblant à des clés de voûte, et qui vont soutenir le sable situé plus haut dans la colonne. C’est ce que montre le dessin ci-contre, issu d’une simulation numérique [1]. La couleur représente la pression que supporte chaque bille, et montre clairement que des arches se dessinent d’une paroi à l’autre.

En présence d’un écoulement, les arches provoquent ce qu’on appelle l’écrantage de Janssen : quand le sable s’écoule, de telles arches se font et se défont en permanence. et elles protègent en quelque sorte le bas de la colonne des pressions élevées : c’est ce qui peut expliquer que la vitesse d’écoulement ne soit pas liée à la hauteur de la colonne de sable.

La physique de ces arches a beau être affreusement compliquée, c’est grâce à elles que la vitesse d’écoulement du sablier est constante, le rendant si pratique à utiliser !

Billets reliés :

Sur les écoulements granulaires L’effet Noix du Brésil, qui parle du mouvement des noix du Brésil dans un pot de cacahuètes.

Sur les fluides non-newtoniens : Jésus et la Maïzena

Pour aller plus loin : la rhéologie des écoulements granulaires

Petit échauffement avant d’aller plus loin : la loi de Toricelli peut se démontrer simplement à partir du théorème de Bernoulli. Ce dernier s’écrit

\(\frac{1}{2} \rho v^2 + \rho g h + P = constante\)

On peut voir ce théorème comme une équation de conservation de l’énergie (volumique), avec trois termes : énergie cinétique, énergie potentielle de pesanteur et pression (je vous laisse vous convaincre que la pression est bien une énergie volumique). Si on applique ce théorème en haut de la colonne, et qu’on dit que la vitesse y est nulle et la pression est celle de l’atmosphère, on trouve que la constante vaut \(\rho g h + P_0\). Si on applique ce théorème au bas d’une colonne dans laquelle le trou est bouché, qu’on écrit que la vitesse y est aussi nulle, on retrouve la fameuse pression hydrostatique \(P=P_0+\rho g h\). Maintenant si on perce un trou, on doit écrire qu’au niveau du trou la pression est celle de l’atmosphère, et on tire donc \(\frac{1}{2} \rho v^2 +P_0 = \rho g h + P_0\), et donc \(v=\sqrt{2gh}\).

Un autre aspect intéressant de ces écoulements granulaires concerne la façon dont on peut simuler un écoulement granulaire « presque » comme un fluide normal. Une astuce imaginée par des équipes françaises [2,3] consiste à décrire l’écoulement granulaire comme un fluide dont la viscosité n’est pas constante, et est reliée à l’existence d’un coefficient de friction local dans le fluide. Cette méthode s’appelle la rhéologie du \(\mu(I)\), du nom du coefficient de frottement que l’on utilise. Ces idées ont eu un très fort retentissement dans le domaine des écoulements granulaires.

Pour ceux que ça intéresse, on définit le nombre inertiel \(I\) de la manière suivante

\(I = \frac{\dot{\gamma}d}{\sqrt{P\rho}}\)

où d est le diamètre des particules, \(\rho\) la masse volumique et \(\dot{\gamma}\) le taux de cisaillement.

Le coefficient de friction (définit par \(\mu\equiv\frac{\tau}{P}\)) est ensuite pris comme une fonction de I

\(\mu(I)=\mu_S+\frac{\Delta\mu}{I_0/I+1}\)

avec \(\mu_S\) le coefficient de friction statique, et \(\Delta\mu\) et \(I_0\) des constantes. On a alors pour la viscosité :

\(\eta \equiv \frac{\tau}{\dot{\gamma}} = \frac{\mu(I) P}{\dot{\gamma}}\).

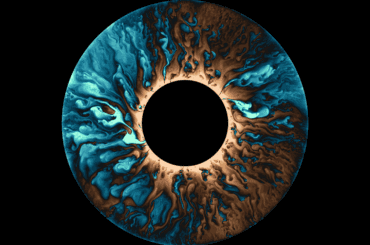
Ce qu’il y a de fort, c’est qu’avec ces définitions, on peut simuler un écoulement granulaire comme un fluide presque normal (enfin non-newtonien quand même), mais sans simuler le détail de chaque grain. Les résultats sont spectaculaires, car on retrouve par exemple l’effet d’écrantage de la pression, comme sur l’image ci-contre tirée d’une chouette publication toute récente d’une autre équipe française [4].

Dans cette image, les couleurs représentent la pression, et on observe très bien que la pression juste au dessus du trou est très réduite comparée à ce que ce cela devrait être pour un fluide comme l’eau.

Avec ces simulations, on peut montrer que l’hypothèse des arches n’est pas nécessaire, ou du moins incomplète ! En effet on se sait expérimentalement que les arches ne peuvent pas se former quand on considère une colonne très large par rapport à sa hauteur, et pourtant l’effet d’écrantage existe quand même. Grâce à la rhéologie du \(\mu(I)\), les chercheurs français ont montré que même sans arches (qui ne sont pas simulées dans leur calcul), le fait d’avoir un seuil d’écoulement frictionnel est suffisant pour expliquer la réduction du champ de pression et la loi de Beverloo.

Question ouverte pour ceux qui ont eu le courage de lire jusqu’ici : je n’ai pas réussi à comprendre comment on pouvait à partir de la description du \(\mu(I)\) retrouver une description d’un fluide newtonien. J’imagine que ça doit être le cas si on fait tendre les bonnes choses vers les bonnes valeurs (genre diamètre des particules vers 0, friction statique vers 0, etc.). Mais je n’ai pas trouvé…

[1] Carlevaro, C. Manuel, and Luis A. Pugnaloni. « Arches and contact forces in a granular pile. » The European Physical Journal E 35.6 (2012): 1-7.

[2] MiDia, G. D. R. « On dense granular flows. » Eur. Phys. J. E 14 (2004): 341-365.

[3] Jop, Pierre, Yoël Forterre, and Olivier Pouliquen. « A constitutive law for dense granular flows. » Nature 441.7094 (2006): 727-730.

[4] Staron, Lydie, P-Y. Lagrée, and Stéphane Popinet. « The granular silo as a continuum plastic flow: The hour-glass vs the clepsydra. » Physics of Fluids 24 (2012): 103301.