Un ascenseur pour l’espace

Imaginons que vous souhaitiez placer un satellite en orbite. Avec les fusées actuelles, il vous en coûtera environ 10 000 €/kg. Pour tenter de réduire drastiquement ce coût, plusieurs scientifiques ont proposé l’idée folle de construire un ascenseur géant pour monter les satellites dans l’espace.

Parmi eux, l’écrivain de science-fiction Arthur C. Clarke qui en 1979 évoque cette idée dans un de ses romans, en ajoutant qu’il est convaincu que ce genre d’ascenseur sera construit un jour, mais « seulement 50 ans après que tout le monde ait arrêté de rire ». Alors voyons s’il est temps d’arrêter de rire !

La tour de Tsiolkovsky

L’idée d’aller dans l’espace avec un ascenseur ne date pas d’hier. En 1895, l’ingénieur russe Konstantin Tsiolkovsky s’inspire de la récente construction de la Tour Eiffel pour proposer tout simplement de construire une tour géante de quelques milliers de kilomètres de haut.

Le principal souci d’une telle tour serait qu’elle ne pourrait même pas supporter son propre poids ! En effet on sait qu’aucun matériau n’est infiniment résistant, et qu’ils peuvent tous casser si on leur applique une pression suffisante : la limite de pression qu’un matériau peut supporter s’appelle sa résistance en compression. Cette résistance, souvent notée \(\sigma\), se mesure en méga-Pascals (MPa), et vaut par exemple 100 MPa pour les bétons les plus performants.

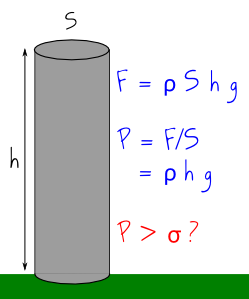La partie de la tour qui subit la plus forte pression, c’est le rez-de-chaussée. Pour savoir si une tour peut soutenir son propre poids, il faut donc voir si la pression subie par le rez-de-chaussée dépasse la résistance en compression du matériau utilisé. Comme illustré ci-contre, la pression subie pour une tour de hauteur \(h\) est \(P= \rho g h\), où \(\rho\) est la masse volumique et \(g\) l’accélération de la pesanteur. La tour résiste donc tant que \(P > \sigma\), c’est-à-dire tant que sa hauteur \(h\) est inférieure à

\(h_C = \frac{\sigma}{\rho g},\)

une quantité appelée la hauteur critique. Celle-ci dépend des caractéristiques du matériau : elle est d’autant plus élevée que le matériau est résistant et léger.

Pour le béton, on trouve une hauteur critique de 4km. Avec de l’acier performant, on peut atteindre 50km. Et pour l’un des matériaux les plus résistants que l’on connaisse, le kevlar, la hauteur critique est d’environ 200km. Pas si mal, mais vous voyez qu’on est encore loin des milliers de kilomètres qu’il nous faudrait pour une tour spatiale !

Une tour pas si lourde que ça

Pour essayer de défendre l’idée de la tour de Tsiolkovsky, on peut noter que le calcul ci-dessus n’est pas tout-à-fait correct. En effet on sait que plus on s’éloigne de la Terre, plus le champ gravitationnel est faible.

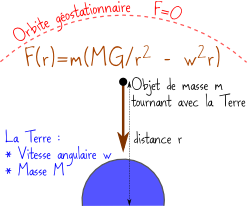De plus, puisque notre tour va évidemment tourner avec la Terre, elle va subir une force centrifuge dirigée vers le haut, et qui s’oppose donc à son poids. Le schéma ci-contre vous montre la force nette que l’on subit si on se trouve à une distance \(r\) du centre de la Terre tout en tournant avec elle.

Au niveau de l’orbite géostationnaire (située 36000 km au dessus de nos têtes), cette force nette est nulle : la force centrifuge compense  exactement l’attraction terrestre (au passage, c’est aussi A. Clarke qui a imaginé le concept d’orbite géostationnaire…)

Du fait de ces deux observations,  la pression sur la base de la tour sera moindre que ce que nous avons estimé juste avant. Le calcul exact est assez simple [1], et on trouve qu’une tour s’étendant jusqu’à l’orbite géostationnaire exercera une pression égale à seulement 14% de celle qu’on obtenait par le calcul précédent. Cela veut dire qu’avec un matériau possédant une hauteur critique de « seulement » 5000km, on pourrait construire notre tour.

Il reste deux problèmes : le premier c’est de trouver un matériau de ce genre, le second c’est que même si elle résiste à son propre poids, une tour de 36 000km de haut a de forte chance de ployer ! Prenez l’exemple d’un arbre extrême, de mettons 10cm de diamètre et 100m de haut. Le rapport hauteur/diamètre est de 1000, et on imagine fortement qu’un tel arbre va ployer facilement sous son poids. Prenez ce facteur 1000 pour notre tour, et vous trouvez que sa base devrait faire 36 km de diamètre ! Pas très réaliste.

Pour résoudre le problème du ploiement, il existe une solution : faire une tour en tension.

La tour en tension

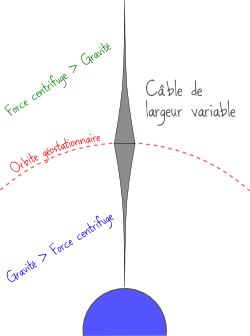En 1975, l’ingénieur américain J. Pearson a exposé le concept de la tour en tension [1], qui en pratique serait plutôt un câble tendu qu’une tour. Si vous reprenez l’expression de la force nette (somme de l’attraction gravitationnelle et de la force centrifuge), vous constaterez qu’au-delà de l’orbite géostationnaire, c’est la force centrifuge qui gagne !

Et donc si la tour s’étend suffisamment au-delà de l’orbite géostationnaire, la force centrifuge peut équilibrer l’attraction terrestre, de sorte que le câble soit tendu mais subisse une force nette nulle. En pratique, l’extrémité inférieure du câble touchera juste la terre sans s’y appuyer !

Pour minimiser les contraintes mécaniques, J. Pearson a calculé que l’épaisseur du câble devait varier : maximale au niveau de l’orbite géostationnaire et minimale au niveau du sol. Plus précisément, il a relié le ratio entre le diamètre minimal et le diamètre maximal à la hauteur critique du matériau utilisé [1].

Mais le problème du choix du matériau demeure : avec de l’acier de hauteur critique 50km, il faudrait un câble dont le diamètre au niveau de l’orbite géostationnaire soit \(10^{40}\) fois plus élevé que le diamètre au niveau du sol. Alors qu’avec un matériau de hauteur critique 10 000 km, ce ratio serait inférieur à 2. Il faut donc définitivement trouver un nouveau matériau plus léger et plus résistant !

Les nanotubes de carbone

Depuis quelques années, l’idée de l’ascenseur spatial est ressortie des cartons, et ce grâce à la découverte d’un nouveau matériau : les nanotubes de carbone. Mis en évidence dans les années 1990, ce sont sont des structures cylindriques creuses, de 1 à 10 nanomètres de diamètre, qui sont formées d’atomes de carbone arrangés en hexagones (voir ci-contre).

Dans beaucoup de domaines, les nanotubes de carbone possèdent des propriétés exceptionnelles : légers, conducteurs, … et extrêmement résistants mécaniquement ! Il paraît même que ma raquette de badminton en contient.

Actuellement, les meilleurs nanotubes mesurés possèdent des résistances approchant 100 000 MPa, et la limite théorique semble se situer vers 300 000 MPa, soit 100 fois plus que le kevlar ou les meilleurs aciers, le tout en étant bien plus légers !

Avec de telles valeurs, une longueur critique supérieure à 10000 km paraît atteignable : pour faire notre ascenseur spatial, on n’a plus qu’à construire un câble en nanotubes de carbones !

Et c’est pour quand ?

Bien que l’idée paraisse encore très exotique, plusieurs entités s’intéressent à l’avenir possible de l’ascenseur spatial. La NASA a lancé il y a 5 ans le Strong Tether Challenge, doté d’un prix de 2 million de $ à qui fabriquera une corde d’un mètre, pesant moins d’un gramme et capable de supporter une traction de 7500 Newtons !

Dans le même ordre d’idée, un brevet sur le concept d’ascenseur spatial  a été déposé par la société d’aviation Lockheed Martin (voir US6491258)  !

Pour ceux qui rêveraient déjà d’atteindre le 36ème ciel spatial en ascenseur, on peut dores et déjà modérer l’enthousiasme en soulignant que de nombreux points restent à résoudre avant de construire notre câble d’ascenseur : celui-ci devra en effet résister notamment aux vents, à l’attraction de la Lune, aux rayons cosmiques ainsi qu’à tous les objets qu’on peut croiser dans l’espace, le tout bien sûr sans perdre ses propriétés mécaniques ! Disons que l’on peut encore rire pendant une bonne dizaine d’années…

Ajout du 28/02 : pour un calcul un peu analogue à celui de la tour la plus haute constructible avec un matériau donné, allez lire ce billet de Xochipilli sur la hauteur maximale des montagnes sur les différentes planètes.

[1] J. Pearson, The orbital tower, Acta Astronautica Vol 2 (1975) p785