L’astéroïde troyen de la Terre

Un troyen, ça n’est pas seulement un beau guerrier antique. C’est aussi un astéroïde plus ou moins gros qui squatte l’orbite d’une planète, mais sans la déranger.

Si l’on en connait quelques milliers près de Jupiter, jamais aucun n’avait été détecté sur l’orbite de la Terre. Eh bien c’est maintenant chose faite, grâce à une récente publication [1] révélant l’existence du mystérieux astéroïde troyen 2010-TK7.

Ménage astronomique à trois

Considérons un système simple : la Terre qui tourne autour du Soleil; et ajoutons un troisième larron : un petit astéroïde. Si sa masse est suffisamment faible, il ne va pas perturber la course de la Terre autour du Soleil, mais cet astéroïde subira l’influence des deux astres.

Suivant où se trouve l’astéroïde, on peut en gros distinguer deux cas de figure :

• s’il est suffisamment proche de la Terre, il va orbiter autour d’elle, à la manière de la Lune;
• s’il est assez loin de la Terre, il va plutôt être attiré par le Soleil et établir sa propre orbite autour de lui.

Comme on peut s’en douter, il existe un cas intermédiaire rarissime, celui où notre astéroïde se trouve exactement à la bonne distance entre la Terre et le Soleil, de sorte qu’il est pile à l’équilibre entre les deux. Cette position très précise s’appelle le point de Lagrange L1.

J’ai réalisé la vidéo ci-dessous pour illustrer ces trois cas de figure, le dernier étant le fameux point L1. Le Soleil est en jaune, la Terre en rouge et notre astéroïde en noir.

Comme vous avez pu le voir, quand un astéroïde est au point de Lagrange L1, son orbite est synchrone avec celle de la Terre. Mais dès qu’il est un tout petit peu plus proche ou plus loin, on retombe dans l’un des deux cas précédents.

Les différents points de Lagrange

Le point L1 situé entre la Terre et le Soleil n’est pas le seul point exceptionnel qui permette d’avoir une orbite synchrone avec la Terre. Il en existe en réalité cinq, et ils sont notés L1, L2, L3, L4 et L5, en référence à leur découvreur, le mathématicien Joseph Lagrange. Ces cinq points sont des endroits où les forces exercées par la Terre et le Soleil s’équilibrent subtilement, de sorte qu’une orbite synchrone devient possible.

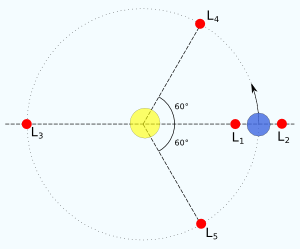La figure ci-contre montre la position des 5 points de Lagrange. Nous avons déjà découvert le point L1, situé entre la Terre et le Soleil. Le point L2 est à peu près à la même distance, mais de l’autre côté de la Terre.

Le point L3 est particulièrement attrayant, car situé en opposition de la Terre, de l’autre côté du Soleil. C’est à cet endroit que pourrait se trouver l’Anti-Terre, une hypothétique planète jumelle de la Terre qui nous serait en permanence cachée par le Soleil.

Sauf que tout cela n’est vrai que dans les oeuvres de science-fiction ! On a en effet depuis longtemps pu vérifier qu’aucune planète ne se trouve au point L3. Et d’ailleurs ce serait bien malheureux pour elle, car ce point est un point instable !

Stabilité ou instabilité ?

Je vous ai dit que les points de Lagrange pouvaient se voir comme des points d’équilibre. Mais comme souvent en physique, certains de ces équilibres sont stables et d’autres instables. Les points L1, L2 et L3 sont des points d’équilibre instable : à la moindre perturbation on s’en écarte rapidement, comme une bille posée au sommet d’une colline. Vous pouvez vous en rendre compte si vous regardez attentivement la toute fin de la vidéo que j’ai mise ci-dessus : on voit qu’après un tour complet synchrone, notre astéroïde situé en L1 finit par quitter cette position et à retomber dans la situation d’orbite autour du Soleil.

L3 est aussi un point instable, c’est pour cela que ça n’est pas un bon endroit pour y cacher l’Anti-Terre ! Par contre pour y planquer temporairement une armée d’invasion spatiale, c’est une bonne idée ! Signalons également que bien que le point L1 soit instable, c’est un bon endroit pour y mettre certains satellites artificiels, notamment ceux destinés à l’observation du soleil. Ainsi ils ne sont pas gênés par la Terre ou la Lune. Et si le satellite dispose de petits moteurs, il peut contrôler sa trajectoire pour rester sur le point L1.

Les points L4 et L5

Bonne nouvelle, les deux derniers points L4 et L5 sont plus intéressants, car ils sont stables. Leur position se trouve exactement sur l’orbite terrestre, respectivement en avance et en retard d’un angle de 60°, comme montré sur le dessin situé plus haut. La stabilité de ces points leur permet d’accueillir des astéroïdes troyens sur des périodes très longues.

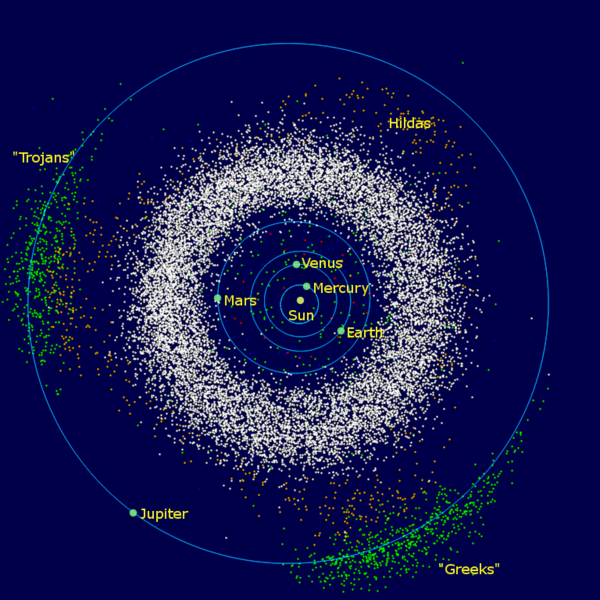
Autour de Jupiter, on a ainsi détecté plusieurs milliers d’astéroïdes au voisinage des points L4 et L5 (voir ci-contre), et on les a baptisés des noms des héros de l’Illiade d’Homère : pour les astéroïdes situés en L4, des noms de héros du camp grec, et pour les L5 des noms de héros troyens. C’est de là que vient le terme !

La vidéo ci-dessous montre l’orbite du point de Lagrange L4 (qui est stable), et montre également ce qui se passe si on essaye de mettre un astéroïde sur l’orbite terrestre, mais en avance de 48° ou 72° au lieu de 60° : les trajectoires ne sont pas synchrones avec la Terre !

« LE » Troyen de la Terre

Depuis quelques semaines, c’est officiel, on a localisé le premier astéroïde troyen de la Terre. Il se nomme 2010-TK7, et se trouve au point L4. Ou plus exactement au voisinage du point L4, car la stabilité de ce dernier autorise des trajectoires qui oscillent autour de lui.

Si vous regardez où se trouve L4, vous comprendrez que ça n’est pas facile de voir un astéroïde dans cette région, car c’est un endroit qui se trouve en permanence dans la lumière du Soleil. Quand on sait que 2010-TK7 ne fait probablement que 300 mètres, autant chercher une aiguille dans une botte de foin ! Et c’est ce qu’on fait les auteurs du papier publié fin juillet dans Nature [1], à partir de données collectées dans le domaine des émissions infra-rouges.

Avec la découverte de ce troyen sur notre orbite, j’espère que vous vous sentez moins seuls !

Pour aller plus loin…

Pour les curieux, j’ai réalisé les deux vidéos précédentes en Matlab avec le solveur ode113. J’ai choisit de m’éloigner de la réalité en prenant une orbite circulaire (et pas légèrement excentrique comme l’est celle de la Terre), et aussi j’ai choisit un rapport de 1 à 10 entre la masse de la Terre et celle du Soleil.

Ce ratio permet d’avoir des trajectoires plus visibles sur le dessin, mais en contrepartie la stabilité des trajectoires est beaucoup plus difficile à obtenir qu’avec le ratio réel. Pour que mon orbite L1 fasse un tour complet sans diverger, j’ai dû ajuster la position de l’astéroïde avec 10 chiffres significatifs ! J’ai pris une distance de 0.7175125871. Si je change ne serait-ce que le dernier de ces chiffres, la trajectoire décroche avant d’avoir fait un tour complet. On mesure à quel point la trajectoire d’un point instable est sensible !

A contrario, pour se rendre compte du fait qu’autour d’un point stable, on peut avoir des trajectoires assez oscillantes sans décrocher, vous pouvez aller voir une vidéo de la NASA, qui montre la complexité de l’oscillation de 2010-TK7 autour de L4

Références et billets reliés

[1] Martin Connors, Paul Wiegert & Christian Veillet, Earth’s Trojan asteroid, Nature 475 (2011) pp481

Sur Science Etonnante : Aller à l’infini en un temps fini, une histoire d’objets astronomiques qui s’envoient en l’air vite et loin;

Illustrations :

• Brad Pitt dans un extrait du film Troie
• Modification personnelle du fichier wikimédia Lagrange_very_massive
• Fichier wikimédia InnerSolarSystem