Ondes gravitationnelles ? Inflation ? Ou les deux ?

La découverte a été annoncée, la nouvelle a fait le tour du monde et les gros titres des journaux. Tout le monde en a déjà parlé, et les blogs scientifiques bien évidemment ne sont pas en reste (voir à ce sujet les billets de mes collègues cafetiers des sciences Ca se passe là-haut et Dr Goulu)

Mais qu’est-ce que je vais bien pouvoir raconter qui n’a pas déjà été dit ?

Eh bien je vais tenter de vous expliquer dans le détail ce que toute cette agitation signifie !

Quand je dis « dans le détail », je veux aller jusqu’à vous montrer les figures qui ont été publiées par les auteurs, et que vous compreniez vraiment ce qu’elles signifient. Et aussi vous faire sentir pourquoi il est légitime de s’enthousiasmer, mais aussi pourquoi il est légitime d’être prudent.

Les concepts que l’on va croiser (inflation cosmique, ondes gravitationnelles, fluctuations de la polarisation…) peuvent paraître franchement intimidants, mais je vais prendre le temps d’expliquer tout ça tranquillement. Alors je vous promets que le voyage ne sera pas si compliqué, par contre il sera un peu plus long que d’habitude ! C’est l’avantage de raconter les choses dans un blog, on dispose de toute la place qu’on veut.

L’expansion de L’Univers

Pour comprendre ce dont il va être question ici, il faut revenir un peu aux bases de la cosmologie, à savoir le modèle du Big-Bang. Tout commence en 1915, année où Einstein publie sa théorie de relativité générale. Celle-ci permet de décrire la force de gravitation, tout comme le faisait la théorie de Newton. Dans bien des situations pratiques, les deux théories font des prédictions similaires, mais celle d’Einstein repose sur des concepts radicalement nouveaux. Alors que Newton décrivait la gravité à partir d’une force immatérielle, Einstein place son origine dans la courbure de l’espace-temps. Les masses courbent l’espace-temps et cette déformation modifie le mouvement des objets alentours.

Peu après sa publication, de nombreux physiciens et mathématiciens ont essayé d’appliquer les équations d’Einstein à tout un tas de situations. La plus ambitieuse consiste à les appliquer à l’Univers tout entier ! Et si on fait cela, on tombe sur une conclusion étonnante : l’Univers n’est pas forcément statique mais pourrait être en expansion ! L’histoire est connue, Einstein n’y croyait pas du tout, mais pour une fois il avait tort : en 1929, l’astronome Edwin Hubble montre en observant les galaxies que l’Univers est bien en expansion !

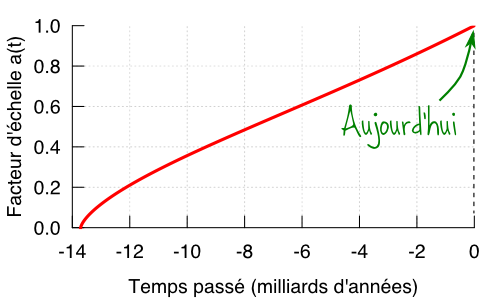
En confrontant les observations d’Hubble (et de tout ses successeurs !) avec les équations d’Einstein, on peut arriver à un modèle assez simple de l’évolution de l’Univers, et qui est représenté ci-dessous :

Cette courbe définit ce qu’on appelle le facteur d’échelle \(a(t)\) : ce facteur nous montre l’évolution des distances dans l’Univers, rapportées à leurs valeurs actuelles. Si on appelle t=0 l’instant présent, on a par définition \(a(0) = 1\) et \(a(t)\) est inférieur à 1 dans le passé.

Par exemple il y a 8 milliards d’années, le facteur d’échelle valait à peu près 0.5. Cela veut dire qu’il y a 8 milliards d’années, toutes les distances était deux fois plus petites. Si deux galaxies sont séparées aujourd’hui de 2 millions d’années-lumières, il y a 8 milliards d’années elles n’étaient séparées que de 1 million d’années-lumières.

Ce que l’on voit, c’est que quand on remonte dans le temps, la valeur de \(a(t)\) diminue jusqu’à tomber à 0, il y a environ 13.8 milliards d’années : voilà ce qu’on appelle le Big Bang ! Il y a 13.8 milliards d’années, le facteur d’échelle était très très petit, l’Univers était dans une phase très comprimée, très dense et très chaude, et il s’est étendu à partir de là.

(Si toutes ces idées vous paraissent encore floues, je donne plus de détails dans ce billet sur l’éloignement des galaxies)

Le modèle du Big Bang a depuis reçu de nombreuses confirmations expérimentales, dont la plus importante est l’existence du rayonnement fossile (ou fond diffus cosmologique), un écho d’une période très chaude du Big-Bang, et dont on va longuement reparler.

Quelques détails qui clochent

Malgré toutes ces bonnes nouvelles sur la validité du modèle du Big Bang, il y a quand même quelques aspects qui ne collent pas bien.

Le premier de ces détails, c’est ce qu’on appelle parfois le problème de l’horizon. Imaginons que vous regardiez le ciel dans deux directions opposées. Aussi loin que l’on sache regarder avec des télescopes, l’aspect de l’Univers dans ces deux directions sera très similaire : même répartition des galaxies, même structure du rayonnement fossile, etc. On dit que l’Univers est homogène même aux très grandes échelles. Et pourtant à cause de l’expansion de l’Univers, les régions lointaines situées dans une direction donnée n’ont jamais eu le temps d’être contact avec les régions lointaines situées dans la direction opposée. C’est ce qui est figuré sur le schéma ci-dessous.

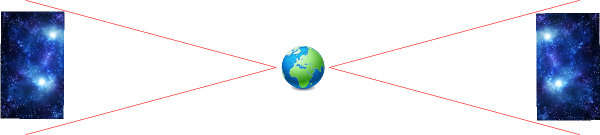Nous avons donc des régions de l’Univers qui se ressemblent beaucoup, et qui pourtant – d’après la théorie classique du Big Bang – on été séparées tellement vite à la naissance qu’elles n’ont jamais pu être en contact. Voilà qui est extrêmement improbable, et a donc mis la puce à l’oreille des cosmologistes. Prenons une analogie : c’est comme si on vous montrait deux lacs en vous disant qu’ils n’ont jamais été en contact l’un avec l’autre, mais qu’en analysant leur eau, vous trouvez que leur composition est quasiment identique.

Autre détail qui cloche dans le modèle classique du Big Bang : la platitude de l’Univers. La théorie d’Einstein nous dit que l’espace temps peut être courbé. Au niveau global, on peut envisager que l’Univers possède une courbure positive (comme sur une sphère) ou négative (comme sur une selle de cheval). Cas intermédiaire juste entre les deux : l’Univers peut en principe aussi posséder une courbure nulle et être plat.

Et quand on mesure effectivement la courbure de l’Univers, c’est précisément ce qu’on trouve. L’Univers est plat, tristement plat, désespérément plat ! Cette observation titille également les cosmologistes car il semble que l’Univers contienne juste exactement la quantité de matière qui est nécessaire pour être plat. Or on sait que cette situation est instable : si aujourd’hui la quantité de matière est « pile-poil » la bonne, alors dans le passé elle a du être « fabuleusement pile-poil ». Et ça aussi c’est improbable.

Il existe encore quelques autres problèmes similaires dans le modèle classique du Big Bang, et je ne vais pas les énumérer; mais l’important à comprendre, c’est que ce sont ces problèmes qui ont conduit à l’apparition de l’idée qui nous intéresse : l’inflation.

L’idée de l’inflation cosmique

Nous l’avons dit, les équations classiques de la cosmologie fonctionnent très bien, mais il y a quelques petits détails improbables qui semblent clocher. Pour les régler, plusieurs scientifiques — dont les plus célèbres sont l’américain Alan Guth et le russe Andreï Linde — ont proposé au début des années 80 une idée radicale : l’inflation cosmique.

Repensez au problème de l’homogénéité de l’Univers : des régions dont on pense qu’elles n’ont jamais été en contact, et qui pourtant se ressemblent…c’est certainement qu’elles ont quand même été en contact un jour ! Guth a alors eu l’idée de modifier les équations de la cosmologie au tout début de la vie de l’Univers pour forcer ce contact initial; et une manière de le faire est d’introduire une phase de croissance exponentielle appelée inflation. Le graphique ci-dessous représente (en rouge pointillés) l’évolution du facteur d’échelle selon le modèle classique (que je vous ai montré ci-dessus), et en bleu une modification possible comportant une phase d’inflation.

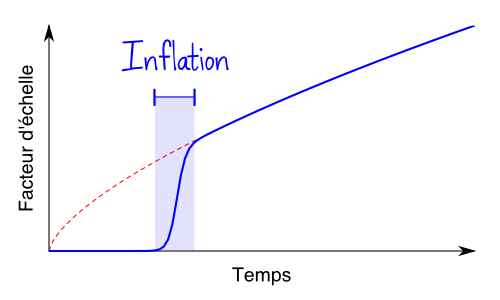Vous voyez qu’avec cette idée, l’Univers ne croit pas tout de suite au début, il a le temps de s’homogénéiser et que toutes les régions se mettent en contact, puis une phase d’inflation très rapide permet de « rattraper » la courbe habituelle, et de suivre ensuite une évolution identique.

Dit comme ça, ça a l’air facile, mais pour que cela fonctionne, la phase d’inflation a dû avoir lieu très tôt dans la vie de l’Univers, et elle a dû être très courte et fabuleusement violente. Je vous donne les chiffres mais ils sont difficile à concevoir : le volume de l’Univers aurait augmenté d’un facteur 10⁷⁸ en 10^-32 secondes ! Je vous laisse calculer le taux de croissance et comparer ce dernier à celui du PIB !

L’idée de l’inflation a l’air très séduisante car elle résout le problème de l’homogénéité de l’Univers, ainsi que les autres petits détails qui clochent. Mais quand même, elle fait appel à des notions extrêmes, très au-delà de la physique que l’on connait ! Il faut donc des preuves expérimentales solides de cette idée. L’autre petit souci, c’est que je vous ai dessiné grossièrement une modification de la courbe du facteur d’échelle qui figure une inflation, mais mathématiquement il existe des tas de façons de le faire. En gros, il existe autant de modèles d’inflation que de physiciens travaillant sur le sujet.

Bref, il est grand temps de chercher une expérience pour prouver l’inflation, et comme l’inflation a été un phénomène d’une violence inouïe, on se dit qu’il doit bien rester quelques traces de cette période ! Et c’est là qu’interviennent les fameuses ondes gravitationnelles.

Les ondes gravitationnelles

Revenons un peu à Einstein. Je vous ai dit que sa théorie de la relativité générale donne une description de la gravité plus précise que celle de Newton. Une des différences, c’est qu’Einstein prédit que la force de gravité peut engendrer des ondes. La situation est très similaire à ce qu’il se passe pour l’électromagnétisme. Le champ électrique est à l’origine de la force électrostatique; et si vous vous mettez à faire varier rapidement un champ électrique, vous allez créer des ondes électromagnétiques qui vont se propager à la vitesse de la lumière. Dans la théorie d’Einstein, c’est pareil ! Dans certaines circonstances il peut se produire des ondes gravitationnelles, qui sont de petites déformations de l’espace-temps qui se propagent elles-aussi à la vitesse de la lumière.

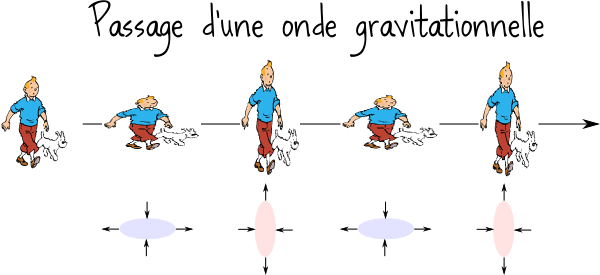
Pour vous rendre compte de ce que cela signifie, le schéma ci-dessous représente ce qu’il arriverait à Tintin s’il était traversé par une onde gravitationnelle : il subirait une série de cycles de contraction/dilatations, de telle manière à ce qu’une contraction dans un sens s’accompagne d’une dilatation dans la direction opposée.

Si vous n’avez jamais vu personne se déformer comme ça dans la rue, c’est normal : c’est que les ondes gravitationnelles sont extrêmement faibles. On estime que les taux de déformation sont au maximum de l’ordre de \(10^{-21}\). C’est tellement petit que les ondes gravitationnelles n’ont encore jamais été directement observées ! Il existe plusieurs expériences en cours à l’aide d’interféromètres géants (comme l’expérience franco-italienne VIRGO). Pour vous faire une idée, les bras de l’interféromètre font plusieurs kilomètres, et l’on espère pouvoir mesurer une déformation de leur longueur de \(10^{-18}\) mètres, soit un milliardième de la taille d’un atome. Pas gagné…d’autant que pour espérer détecter des ondes gravitationnelles, il faut dans l’idéal attendre qu’un évènement cosmique très violent se produise, comme une explosion de supernova, car l’intensité des ondes sera ainsi maximale.

Mais ces circonstances ne sont pas les seules dans lesquelles se produisent des ondes gravitationnelles. Nous l’avons dit, si elle a vraiment existé, l’inflation a été un phénomène d’une violence sans commune mesure : elle a donc engendré une énorme quantité d’ondes gravitationnelles ! Pour les différencier des ondes qui se propagent actuellement, on parle d’ondes gravitationnelles primordiales. La mauvaise nouvelle, c’est que ces ondes ne sont aujourd’hui probablement plus détectables directement; la bonne nouvelle, c’est que si elles ont vraiment existé, elle ont du laisser leur empreinte dans le rayonnement fossile. Voyons pourquoi et comment.

Le rayonnement fossile et ses fluctuations

J’ai déjà eu l’occasion d’écrire un billet détaillé sur le rayonnement fossile lors de la récente publication des résultats du satellite Planck. Rappelons ici les grandes lignes : pendant les 380 000 premières années de l’Univers, il fait très chaud. Bien trop chaud pour que les électrons et les protons se regroupent pour former des atomes. L’Univers est donc fait d’un plasma, et dans cette soupe la lumière ne peut pas se propager normalement, car elle passe son temps à interagir avec les électrons. Au bout de 380 000 ans, tout change ! La température est devenue suffisamment modérée pour que les électrons se marient aux protons pour former des atomes, et tout à coup la lumière peut se propager, car elle n’est plus gênée par les électrons en liberté.

Aujourd’hui encore, on peut observer cette radiation émise il y a presque 14 milliards d’années, et elle baigne l’ensemble de notre Univers. Elle se manifeste sous la forme d’un très faible rayonnement de type « corps noir », et qui correspond à celui qu’émettrait un objet refroidit à 2.7 Kelvin, c’est-à-dire à peine 3 degrés au dessus du zéro absolu. Ce qui est intéressant dans le rayonnement fossile, c’est que puisqu’il a été émit 380 000 ans après le Big Bang, il est l’équivalent d’une photo qui aurait enregistré l’état de l’Univers à cette époque. Mais cet enregistrement est assez difficile à déchiffrer.

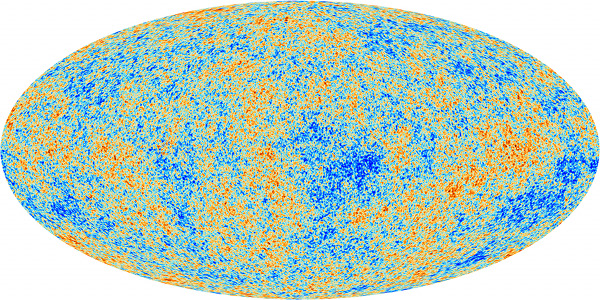
Je vous ai dit que le rayonnement fossile était celui qu’émettrait un corps à 2.7 K, mais en réalité cette température fluctue très légèrement en fonction de l’endroit du ciel que l’on regarde. Dans certaines directions, le rayonnement est un chouilla plus chaud ou froid que la moyenne. Et ce sont ces variations qui portent la trace de l’état de l’Univers primordial. L’image ci-dessous est une carte de température, celle obtenue par le satellite Planck et qui a été publiée il y a quelques mois. Cet ovale représente l’ensemble du ciel autour de nous (c’est comme pour une carte de la Terre : on projette une sphère en un ovale !). On y voit les fluctuations de température en fonction de la direction d’observation. La carte ne donne pas l’échelle de couleur, mais sachez que la taille maximale de ces fluctuations ne dépasse pas 30 millionièmes de degrés !

Le spectre de puissance du rayonnement fossile

Pour décoder complètement ce qui est caché dans les infimes fluctuations du rayonnement fossile, il faut étudier ce qu’on appelle son spectre de puissance. Prenons un exemple simplifié : imaginez que vous observiez les fluctuations de hauteur d’une surface, comme sur le dessin ci-dessous à gauche. Pour caractériser les fluctuations, il faut préciser à la fois l’échelle des fluctuations (la longueur des vagues), et leur intensité (la hauteur). Sur cet exemple, on voit un mélange de fluctuations à grande échelle et à petite échelle.

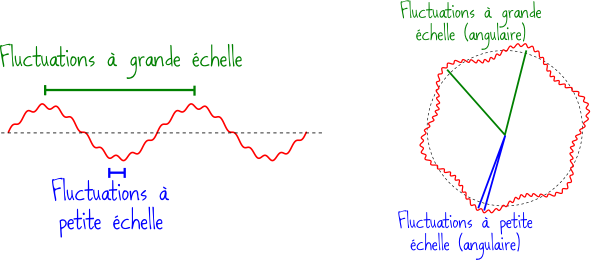Dans le cas du rayonnement fossile, on n’observe pas des variations de température sur une surface plane, mais sur la sphère céleste qui nous entoure. Les fluctuations sont donc caractérisées par leur échelle angulaire et leur intensité. Dans le dessin ci-dessus à droite, on voit un schéma représentant un cercle perturbé par des fluctuations qui sont un mélange de fluctuations de grand angle (ici 60°) et de petit angle (environ 5°).

Voilà donc ce qu’il faut faire pour décoder le rayonnement fossile : mesurer l’intensité des fluctuations en fonction de leur taille angulaire. Le tracé de cette intensité en fonction de l’angle est ce qu’on appelle le spectre de puissance. L’image ci-dessous montre ce spectre tel qu’il a été caractérisé par le satellite Planck. La gauche de la figure représente les fluctuations aux grands angles, et la droite aux petits angles.

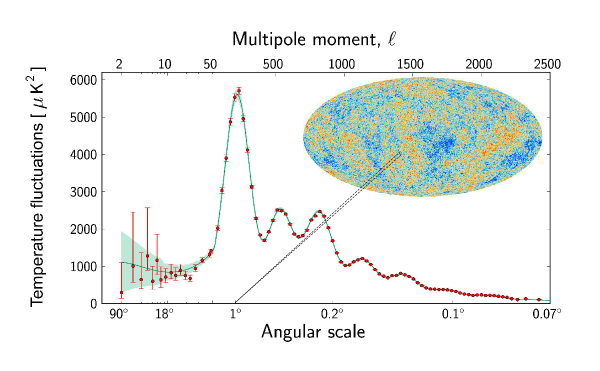On voit qu’il existe par exemple un pic de fluctuations à un angle autour de 1°, et qu’on peut mettre en correspondance avec la carte de température, sur laquelle on observe une granularité dominante de cet ordre.

Ce qu’il y a d’extraordinaire avec ce spectre de puissance, c’est que pour les cosmologistes il s’agit d’un livre ouvert dans lequel on peut apprendre des tas de choses sur le Big Bang. Ainsi la position et la taille des pics nous renseignent sur la densité de matière, la quantité d’énergie noire, etc. De cette manière, les paramètres importants qui entrent dans l’équation du facteur d’échelle \(a(t)\) peuvent être déduits de ce spectre de puissance. Mais à ce stade, ce spectre ne nous renseigne que sur les équations de la cosmologie « normale », il n’est pas encore question de l’inflation…mais ça va venir !

La polarisation du rayonnement fossile

Malheureusement pour la science, le spectre de puissance tel que je vous l’ai montré ne dit rien sur l’inflation. Il ne nous dit même pas si elle a vraiment existé, même s’il y a des indices favorables. Pour percer ses mystères, il faut aller encore plus loin et regarder la polarisation du rayonnement fossile.

Pour commencer, rappelons ce qu’est la polarisation. La lumière est une onde électromagnétique, et quand elle se propage, le champ électrique qui la constitue est situé dans un plan perpendiculaire à la direction de propagation, comme représenté sur le dessin ci-dessous.

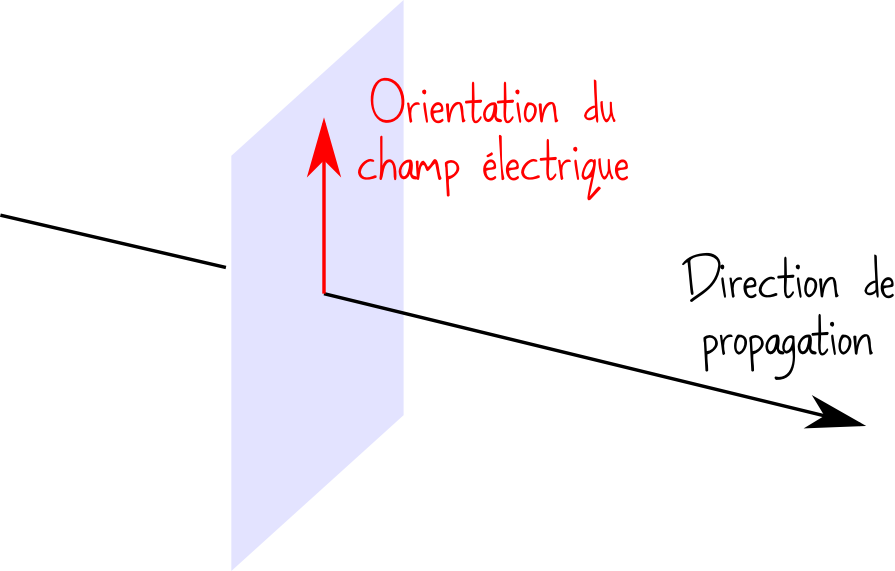En général la lumière de tous les jours est constituée d’un mélange de toutes les directions possibles pour le champ électrique. En moyenne, le champ électrique n’est donc orienté dans aucune direction en particulier, on dit que la lumière est non-polarisée. Mais dans certaines circonstances, il se peut qu’une partie du rayonnement possède une orientation privilégiée pour le champ électrique : on dit alors que la lumière est polarisée. Une circonstance habituelle d’apparition de la polarisation dans notre quotidien, c’est quand la lumière se reflète sur une surface. Par exemple les reflets du soleil dans la mer sont légèrement polarisés, et c’est ainsi que certaines lunettes de soleil (ou certains filtres en photographie) sont capables de les éliminer partiellement.

Pour le rayonnement fossile, ça se passe un peu pareil ! Je vous ai dit que ce rayonnement s’était produit à partir du moment où la lumière a cessé de pouvoir interagir avec les électrons, on appelle ce moment le découplage. Le rayonnement fossile possède en quelque sorte la « mémoire » de sa dernière interaction avec les électrons, et comme dans le cas de la réflexion du soleil sur la mer, cette interaction a pu produire un petit effet de polarisation. Mais cet effet est très faible, car il n’est apparu que dans les tous derniers instants avant le découplage.

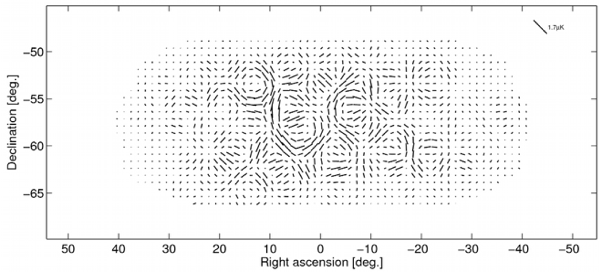
Comme dans le cas de la température, ce qui va nous intéresser, ce sont les fluctuations de la polarisation. C’est-à-dire que si vous regardez le rayonnement en provenance de deux endroits du ciel différents, la polarisation ne sera pas exactement orientée de la même façon. L’image ci-dessous nous montre un exemple de carte de polarisation.

Sur cette carte qui représente un bout du ciel observé par BICEP2, l’orientation de la polarisation en chaque point est indiquée par les petites barres (rappelez-vous, cela indique une direction privilégiée du champ électrique). Vous voyez que cette orientation varie d’un endroit à l’autre, et qu’il y a comme des motifs caractéristiques. C’est la manière dont apparaissent ces motifs qui va nous en apprendre beaucoup, mais pour cela il va falloir décomposer cette carte de fluctuations.

Il existe une manière utile de séparer ces fluctuations de polarisation en ce qu’on appelle deux modes. Le principal est appelé mode E, et il est apparu dans le rayonnement fossile à cause des petites variations de densité qui existaient dans l’Univers au moment du découplage, quand le rayonnement a été émis. Ce mode de fluctuation de la polarisation a été observé pour la première fois en 2002 par l’expérience DASI, et il est maximum pour des variations angulaires de l’ordre de 0.1 degrés. L’intensité de ces fluctuations est seulement de l’ordre de 1 microKelvin !

Malheureusement pour nos affaires, ce mode de fluctuation n’est pas sensible aux éventuelles déformations dues aux ondes gravitationnelles. Ces fluctuations de polarisation que l’on appelle « tensorielles » sont à rechercher dans un autre mode, appelé le mode B. Le problème, c’est que l’intensité du mode B est beaucoup plus faible que le mode E, et jusqu’ici, personne n’avait réussi à le détecter.

Voilà, les préliminaires sont terminés. Nous sommes enfin prêts à parler des résultats annoncés cette semaine ! Résumons où nous en sommes : si inflation il y a eu, elle a engendré des ondes gravitationnelles dites « primordiales », et qui ont déformé la matière présente à l’époque d’une manière bien spécifique. Au moment du découplage, ces déformations ont laissé une légère empreinte dans le mode B des fluctuations de la polarisation du rayonnement fossile. Et ce sont ces empreintes que l’on cherche.

L’expérience BICEP2

Contrairement à l’expérience Planck qui était embarquée dans un satellite, l’expérience BICEP2 utilise un télescope basé au sol et situé au Pôle Sud. Vous pouvez en voir une photo ci-contre. Petite précision : on parle de télescope, mais gardez en tête que le rayonnement que l’on cherche n’est pas du tout fait de lumière visible, mais plutôt de micro-ondes.

Autre différence avec Planck, BICEP2 ne se focalise que sur une partie restreinte du ciel, mais avec l’objectif principal de mesurer les fluctuations de la polarisation. Comme d’autres expériences concurrentes, le choix du Pôle Sud s’explique par une atmosphère pure, sèche, pas trop épaisse et stable.

Il y a un an, le télescope SPT avait déjà annoncé un progrès important car il avait mis en évidence des fluctuations de polarisation en mode B … mais pas celles dues aux ondes gravitationnelles primordiales ! Il existe en effet un autre phénomène qui produit du mode B, et qui est lié à l’existence de lentilles gravitationnelles (dont je parlais ici). Sans rentrer dans les détails, l’interaction du rayonnement fossile avec les objets massif de l’Univers a le mauvais goût de transformer du mode E en mode B. Ce mode B « des lentilles » est beaucoup moins intéressant que le mode B « primordial » l’on cherche, mais on fait heureusement facilement la distinction grâce à l’échelle angulaire des fluctuations. Le mode B « des lentilles » se produit à des échelles angulaires bien plus petites (de l’ordre de 0.1°) que le mode B « primordial », que l’on attend à des échelles de 1°.

Les résultats de BICEP2

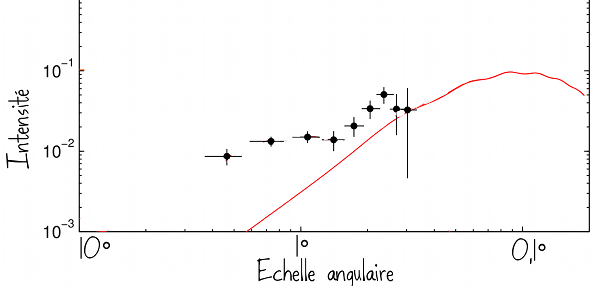
Venons-en enfin aux résulats de BICEP2 annoncés il y a une semaine. Le diagramme ci-dessous montre en noir l’intensité des fluctuations de mode B détectées pour les différentes échelles angulaires, tandis que la ligne rouge représente l’intensité du mode B attendu à cause de l’effet de lentille.

Clairement les points noirs sont au-dessus de la ligne rouge, il y a donc autre chose dans le signal que le mode B des lentilles : c’est bien que l’expérience a trouvé le mode B primordial des ondes gravitationnelles ! (Vous pouvez sortir le champagne)

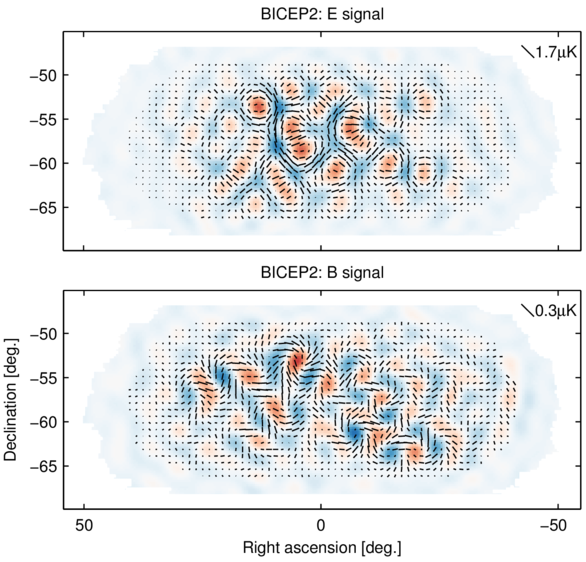
En pratique, si on prend la carte de polarisation que j’ai montré un peu plus haut, qu’on la sépare entre mode E et mode B, on obtient la décomposition ci-dessous.

Vous voyez sur les échelles (coin supérieur droit) que le mode E est plus important que le mode B d’un facteur environ 5. Vous pouvez aussi voir dans ces cartes une sorte de définition de ce qu’on appelle les modes de fluctuation E et B : le mode E produit plutôt des cercles, alors que le mode B produit des tourbillons.

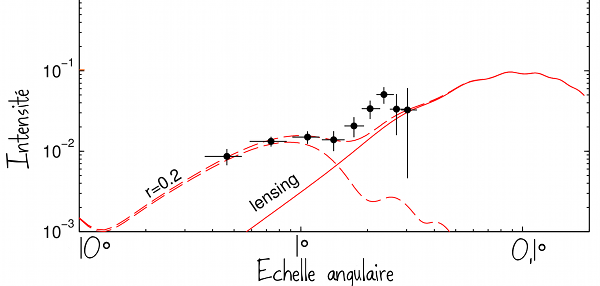
Un point qui a beaucoup agité la communauté cette semaine : le signal observé est finalement moins faible que prévu ! Pour le quantifier, on mesure le ratio (noté \(r\)) entre le mode B et le mode E. Et à l’échelle angulaire qui nous intéresse, ce ratio est d’environ 0.2. Le graphique ci-dessous est le même que celui présenté peu plus haut, mais avec la courbe en pointillés rouges qui indique le niveau théorique des fluctuations de mode B pour une ratio de 0.2. Vous voyez que les points expérimentaux collent bien avec cette estimation !

Interprétation et prudence

La première question que l’on peut se poser avant de parler de prix Nobel, c’est la robustesse du résultat. Est-ce vraiment vrai ? Une raison d’être prudents, c’est que le signal observé est plus fort que prévu. Notamment, avec l’état actuel des données publiées, les scientifiques de la mission Planck annonçaient ne pas avoir vu le mode B, et ils en concluaient que le fameux ratio r devait être inférieur à 0.11…sauf que BICEP2 annonce 0.2 ! Qui a raison ?

Passons en revue les critiques possibles de l’expérience BICEP2. Vu l’ampleur du signal, on peut très certainement exclure un faux positif dû aux statistiques. En revanche, on peut imaginer la possibilité d’une erreur systématique ou d’un autre phénomène causant l’apparition du signal. D’après les scientifiques de la communauté, le nettoyage du signal par les chercheurs de BICEP2 a été fait avec un très grand soin, et il semble que leur méthode de traitement soit donc assez robuste.

Si on veut être un peu pointilleux, il y a quand même un petit truc suspect dans les résultats. Observez les points ci-dessous entouré en vert.

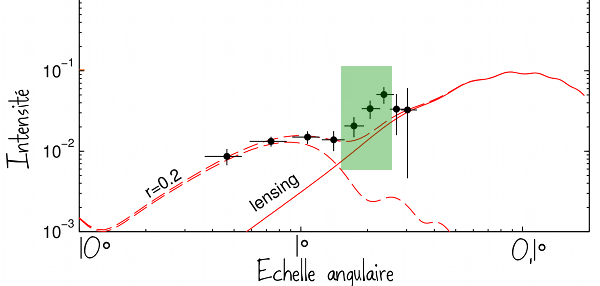Ils sont assez au-dessus de ce qu’on attendrait même en prenant en compte le mode B des lentilles et celui des ondes gravitationnelles. Ça n’est pas extraordinairement significatif, mais c’est à surveiller. Comme ces points sont situés dans une échelle de fluctuations où le mode B des lentilles commence à exister, on peut se demander s’ils ne seraient pas dû à un phénomène de lentille (ou analogue) plus fort que prévu. Et si ce phénomène était réel et contaminait aussi les échelles angulaires plus large, on pourrait craindre que les points détectés aux échelles autour de 1° soient des modes B qui n’aient pas leur origine dans les ondes gravitationnelles primordiales. Heureusement d’autres expériences similaires sont en cours d’analyse (dont un nouveau jeu de données de la mission Planck), et si le résultat est correct on peut espérer en avoir confirmation bientôt. Les résultats de Planck sur la polarisation sont attendus pour Octobre 2014.

Et les modèles d’inflation ?

Jusqu’ici j’ai beaucoup parlé des observations, mais quid des modèles ? (Si cette question théorique vous fatigue d’avance, passez à la partie suivante !) Je vous l’ai dit, il existe autant de modèles d’inflation que de physiciens travaillant sur le sujet. Est-ce que les observations permettent de les discriminer ? La réponse est oui, dans une certaine mesure. Première idée importante : la valeur du ratio r fixe ce qu’on appelle l’échelle de l’inflation, c’est-à-dire le niveau d’énergie (ou de température, c’est pareil) à laquelle elle a pu se produire. Avec les mesures de BICEP2, on trouve une échelle de \(2.10^{16}\) GeV, soit 1000 milliards de fois l’énergie atteinte par le LHC du CERN. Cela confirme que l’inflation a eu lieu dans les tous premiers instants du Big Bang. Autant dire qu’en dehors des observations cosmologiques, des échelles d’énergie pareilles sont inaccessible à l’expérience !

Pour confronter les modèles théoriques aux observations expérimentales, le plus simple est de demander aux modèles de calculer le ratio r, et de comparer cela à l’expérience ! En plus du ratio r, il existe une autre quantité que l’on peut mesurer et qui est prédite par les modèles, et qui s’appelle l’indice spectral, noté \(n_s\). Cet indice très légèrement inférieur à 1 traduit la manière dont le spectre de fluctuation (de température, le premier dont j’ai parlé) décroit quand l’échelle angulaire diminue.

Le diagramme ci-dessous est issue d’une publication de la mission Planck, et date donc d’AVANT la publication de BICEP2. Il montre en abcisses les valeurs possibles de \(n_s\) et en ordonnées les valeurs possibles de \(r\).

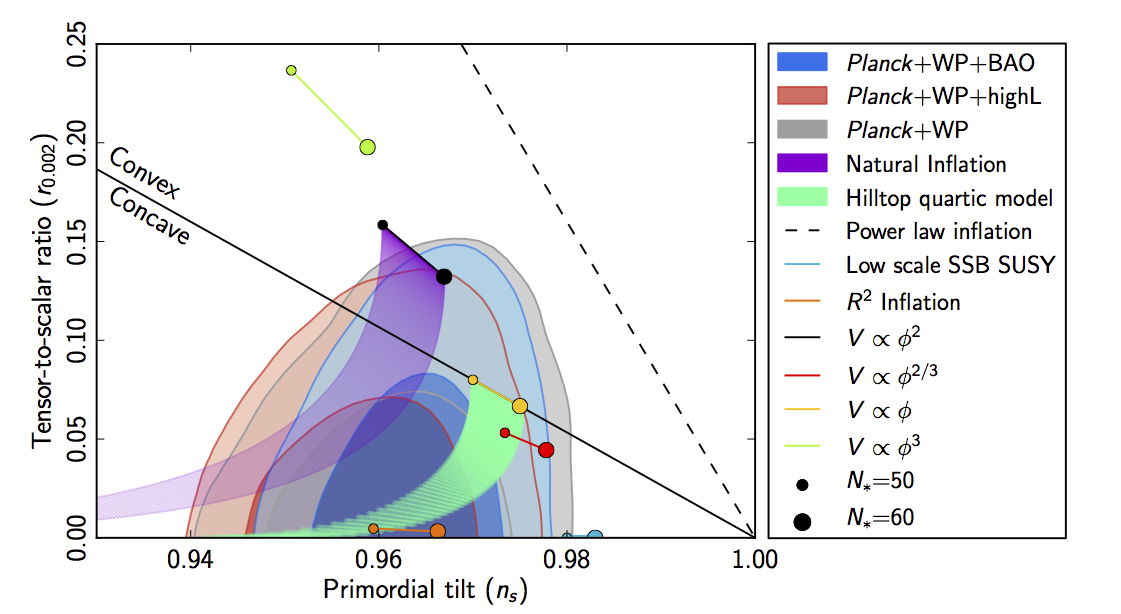On y voit d’une part des contours qui indiquent quels sont les valeurs probables d’après les données de Planck (contours bleu et rouge). Notez que comme je vous le disait, un ratio de 0.2 (en ordonnées) avait a priori été exclu par les observations de Planck ! D’autre part sur ce diagramme, on voit des points qui représentent les prédictions de différents modèles d’inflation (les paires de points, chacun des deux points de la paire correspond à hypothèse différente sur la taille totale de l’inflation, qui vaut \(e^{N^*}\)).

Pour les modèles, les observations de BICEP2 (toujours pareil, si elles sont confirmées…) changent la donne ! En gros pour schématiser, un modèle d’inflation est essentiellement définit par le choix de potentiel que l’on attribue au champ responsable de l’inflation (champ appelé « inflaton« ). Chacun d’entre nous peut choisir son potentiel préféré comme ça lui chante, et la ligne diagonale montre par exemple la limite entre les potentiels convexes et concaves. Notez ainsi les points correspondants à \(V\sim \Phi^2\) (en noir dans la légence), qui était un des modèle d’origine de Linde, un des pères de l’inflation. On voit que son modèle était disqualifié par Planck (il donne un r autour de 0.15), mais revient en force dans la course si la valeur de r est plus élevée !

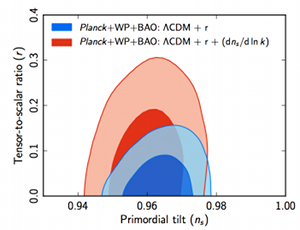Bref la question de la réconciliation de Planck et de BICEP2 devra être au coeur de toutes les attentions dans les prochains mois. A ce sujet, les auteurs de BICEP2 s’en sont tirés par une pirouette. La collaboration Planck avait noté que des valeurs plus élevées de r étaient compatibles avec leurs observations, à condition d’introduire une condition supplémentaire, le fait que l’indice spectral \(n_s\) puisse varier avec l’échelle de fluctuation.

C’est la comparaison qui est faite ci-contre, avec en bleu le même contour bleu que la figure ci-dessus, et en rouge le contour si on autorise \(n_s\) à varier. Si on admet cette possibilité (running spectral index), les résultats de Planck sont moins catégoriques et prédisent seulement r<0.26, ce qui reste compatible avec les nouveaux résultats. C’est cette compatibilité qu’ont mis en avant les auteurs de BICEP2.

Le problème est que cette possibilité d’indice spectral variable n’est pas pour l’instant trop prévue dans les modèles, à moins de les modifier d’une manière assez artificielle. Bref, il reste du boulot aussi pour les théoriciens !

Quelques réflexions personnelles sur l’importance de cette découverte

Quand on annonce en grande pompe des découvertes de ce genre, les journaux sont assez rapides à prédire des prix Nobel comme s’il en pleuvait. Que faut-il penser dans ce cas précis ? Tout d’abord, cette expérience nous parle à la fois d’ondes gravitationnelles et d’inflation. Il y a donc en somme deux découvertes. Laquelle est la plus importante ?

Pour moi la découverte des ondes gravitationnelles est secondaire. En effet il ne s’agit pas d’une mise en évidence directe d’ondes actuellement existantes (comme on espère le faire avec les interféromètres comme VIRGO), mais de la détection de la trace d’ondes ayant existé il y a très longtemps. Pour prendre une analogie, c’est comme si vous cherchiez à prouver qu’il existe des vagues, que vous ne soyez pas capables de les voir directement, mais que vous trouviez une falaise érodée à sa base par les dites vagues. Vous auriez là une preuve indirecte, via une empreinte, de l’existence des vagues. Ici c’est pareil ! Est-ce que ça vaut le Nobel ? Je ne pense pas, car on avait déjà une découverte analogue, qui a déjà valu le Nobel a ses auteurs en 1993. Hulse et Taylor avaient découvert un pulsar et observé que celui-ci perdait de l’énergie à un rythme exactement prédit par le rayonnement d’ondes gravitationnelles. Là aussi, une preuve indirecte. Bref je pense que le Nobel ira peut être un jour à une détection directe des ondes gravitationnelles, mais ici le motif ne me paraît pas suffisant.

Parlons maintenant de l’inflation : est-ce que ça mérite un Nobel ? Si ça se confirme, assurément oui. Comme je le disais au début de ce billet, les modèles d’inflation prédisent des facteurs de croissances démentiels sur des temps incroyablement courts. Il s’agit donc de physique très au-delà du modèle standard ! On pourrait même dire qu’il s’agirait pour la première fois d’une trace expérimentale de la gravité quantique, puisque le signal résulte in fine de fluctuations quantiques de la métrique d’espace-temps.

Au final, on ne peut certainement pas séparer les deux aspects de la découverte, mais l’aspect « inflation » paraît plus important que les ondes gravitationnelles. Et en l’occurrence les journaux ne devraient pas titrer en disant « Einstein avait raison », mais plutôt « Guth, Linde et les autres avaient raison », voire même « Einstein avait tort », puisque l’inflation n’est pas prédite par les modèles classiques de la cosmologie !

Billets reliés, ici et ailleurs

• Sur l’expansion de l’Univers : il y a bien longtemps, dans une galaxie lointaine, très lointaine
• Sur le rayonnement fossile, mon billet publié au moment des résultats de la mission Planck
• Sur les lentilles gravitationnelles, une explication simple avec des boules de Noël
• Chez Dr Eric Simon du blog « Ca se passe là-haut », un billet sur cette découverte
• Un autre billet chez Dr Goulu du blog « Pourquoi Comment Combien » qui partage mon point de vue sur les ondes gravitationnelles
• Pour aller plus loin je vous recommande ces deux billets du blog Résonaances : celui publié avant et celui publié après l’annonce.
• Il y a des FABULEUX tutoriels sur le site de Wayne Hu, professeur à l’Université de Chicago : Il y donne des détails sur le rayonnement fossile, l’apparition de sa polarisation, les modes de fluctuation et les spectres de puissance associés, avec notamment des superbes animations qui montrent comment les spectres changent quand les paramètres cosmologiques varient !
• Voir aussi ce billet qui discute des 3 points un peu suspects

Références

Les 3 principaux papiers de la mission Planck :

[1] Ade, P. A. R., et al. « Planck 2013 results. I. Overview of products and scientific results. » arXiv preprint arXiv:1303.5062 (2013).

[2] Ade, P. A. R., et al. « Planck 2013 results. XVI. Cosmological parameters. » arXiv preprint arXiv:1303.5076 (2013).

[3] Ade, P. A. R., et al. « Planck 2013 results. XXII. Constraints on inflation. » arXiv preprint arXiv:1303.5082 (2013).

Le preprint des résultats de la mission BICEP2

[4] BICEP2 I: Detection Of B-mode Polarization at Degree Angular Scales

Crédits

• La photo du télescope au crépuscule est issu du site l’expérience BICEP2
• Schémas divers (facteur d’échelle, problème de l’horizon, facteur d’échelle avec inflation, ondes gravitationnelles, fluctuations, polarisation) : Science étonnante
• La carte des fluctuations mesurées par Planck
• Le spectre de puissance de Planck est la figure 19 de [1]
• L’image du signal de polarisation totale du mode B n’est pas donnée sur le site, mais je l’ai trouvée dans cette présentation
• Pour le spectre de puissance du mode B, j’ai utilisé 3 fois la figure suivante de la publication BICEP2, que j’ai modifiée et simplifiée pour des besoins pédagogiques.
• Les cartes de polarisation de BICEP2
• Le plot du diagramme r/ns de Planck est la figure 1 de [3]