Il y a bien longtemps, dans une galaxie lointaine, très lointaine…

Il y a quelques mois, une équipe internationale a annoncé la découverte de la plus lointaine galaxie jamais observée [1]. Ce travail se base sur l’analyse de la lumière émise par cette galaxie, et notamment ce que l’on appelle le décalage vers le rouge. Voyons ce qu’est ce décalage et comment son intensité permet de quantifier le chemin parcouru par la lumière depuis son émission par la galaxie.

L’expansion de l’Univers

Le premier ingrédient pour comprendre la manière dont on estime l’âge et la distance des galaxies lointaines est l’expansion de l’Univers. La théorie de la Relativité Générale, mise au point par Einstein au début du XXème siècle, nous prédit que l’espace peut se dilater au cours du temps.

Cette dilatation a comme conséquence que les galaxies s’éloignent les unes des autres, un peu comme si elles vivaient sur un tissu extensible sur lequel on tire progressivement.

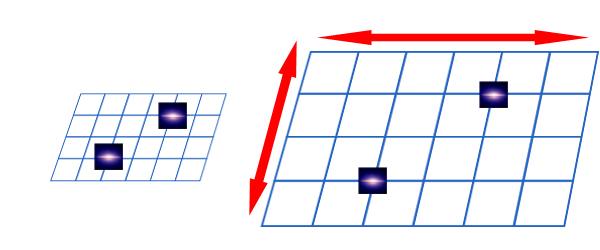A cause de l’expansion de l’Univers, si deux galaxies sont aujourd’hui éloignées d’un milliard d’années lumières, leur distance aura doublé dans 10 milliards d’années.

Le facteur d’échelle

Pour quantifier l’évolution de l’éloignement des galaxies au cours du temps, on utilise une notion appelée facteur d’échelle. On le note \(a(t)\) et il caractérise le degré de dilatation de l’Univers à l’instant t par rapport à aujourd’hui. Si deux galaxies sont aujourd’hui à une distance \(d_0\), alors à l’instant \(t\), elles seront à une distance

\(d(t) = a(t) d_0\)

On peut prendre \(t>0\) pour décrire l’avenir où \(t<0\) pour décrire le passé.

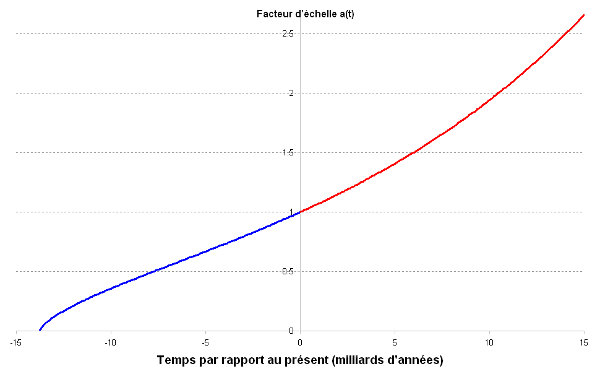
Il existe des équations, dérivées des équations d’Einstein, et qui décrivent l’évolution du facteur d’échelle en fonction de la quantité de matière contenue dans l’Univers. Cela permet donc de retrouver sa valeur dans le passé ou de prédire celle dans le futur. Le graphe ci-dessous vous montre l’évolution du facteur d’échelle par rapport au temps présent t=0 selon le modèle cosmologique actuellement en vigueur [2] . Le passé (t<0) est en bleu et le futur (t>0) en rouge.

On y voit que dans environ 10 milliards d’années, toutes les distances se seront dilatées d’un facteur 2. En revanche il y a 10 milliards d’années, elles étaient environ 1/3 de ce qu’elles sont aujourd’hui. Vous remarquerez que le facteur d’échelle s’annule il y a 13.7 milliards d’années, ce qui signifie qu’à cette époque toutes les distances étaient étaient très très contractées et l’Univers était donc très dense, c’est cela que l’on appelle le big-bang !

Le décalage vers le rouge

Si l’on est capable aujourd’hui d’estimer la distance à laquelle se trouve un objet astronomique très lointain, c’est parce qu’au cours de son voyage vers nous, la lumière qu’il a émise a été modifiée par la dilatation de l’espace.

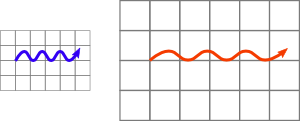On peut comprendre le phénomène en se représentant la lumière comme une onde. Si cette onde voyage dans l’espace et que l’espace se dilate, la longueur d’onde (c’est-à-dire la longueur entre deux pics de l’onde) se trouve augmentée. Ainsi par exemple pour de la lumière bleue (longueur d’onde d’environ 400nm), l’étirement de l’espace d’un facteur 2 peut lui donner au final une longueur d’onde de 800nm, c’est-à-dire rouge.

La relation entre la longueur d’onde initiale (au moment de l’émission) et la longueur d’onde au moment de l’observation est très simple : les longueurs d’onde sont dilatées d’un facteur qui n’est autre que le facteur d’échelle \(\lambda_{obs} = \lambda_{emis}/a(t_{emis})\)

C’est cette propriété qui nous permet de remonter à une distance approximative des objets très lointain : plus l’objet émetteur est lointain, plus la lumière voyage longtemps avant de nous parvenir, plus elle sera décalée vers le rouge par la dilatation de l’espace qu’elle aura traversé [3] !

Les raies d’émission

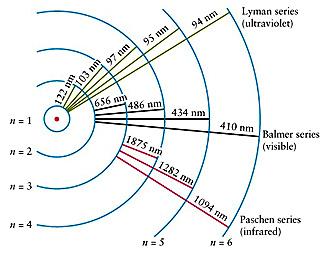Pour pouvoir quantifier le décalage vers le rouge, il nous faut savoir quelle était la longueur d’onde de la lumière au moment de son émission. Cela est possible car nous connaissons les longueurs d’onde d’émission de l’atome d’hydrogène (voir ci-contre), qui est l’élément le plus abondant dans les galaxies.

L’émission la plus courante de l’atome d’hydrogène s’appelle la raie Lyman-alpha, et sa longueur d’onde est de 122nm. Si on est capable de repérer cette raie dans le spectre émis par une galaxie, on peut calculer l’intensité du décalage vers le rouge, et donc remonter au facteur d’échelle au moment de son émission. Voyons cela sur l’exemple de notre galaxie.

UDFy-38135539

Ce nom barbare désigne la galaxie qui nous intéresse, repérée initialement par le téléscope spatial Hubble. L’équipe conduite par M. Lehnert y a ensuite pointé le téléscope VLT pour analyser finement la lumière infrarouge émise. Ils ont alors découvert que la raie Lyman-alpha de cette galaxie se trouvait à environ 1160nm (dans l’infra-rouge), au lieu de 122nm (dans l’ultraviolet) qui est sa longueur d’onde d’émission.

Cela signifie que le facteur d’échelle au moment de l’émission de cette lumière valait environ 122/1160 = 0.105. En regardant le graphique ci-dessus montrant l’évolution du facteur d’échelle, on constate que cette valeur est celle d’il y a 13.1 milliards d’années !

Cette observation du décalage vers le rouge de la raie Lyman-alpha permet donc d’estimer que la lumière que l’on observe de la galaxie UDFy-38135539 a été émise il y a 13.1 milliards d’années. Ceci en fait la galaxie la plus vieille et la plus lointaine jamais observée !

[1] Le papier de Nature : M. Lehnert et al., Spectroscopic confirmation of a galaxy at redshift z=8.6, Nature 467,  p940 (2010)

[2] Pour les furieux, le modèle utilisé ici est le « Lambda-CDM » dont le facteur d’échelle obéit à une équation différentielle assez simple

\(\frac{da}{dt} = H_0 \sqrt{\Omega_M a^{-1}+\Omega_{\Lambda}a^2 }\)

où dans l’état actuel des connaissances de notre univers, \(1/H_0\) est le temps de Hubble et vaut 13.8 milliards d’années, \(\Omega_M\) est la densité de matière et vaut 0.27 et \(\Omega_{\Lambda}\) est la densité d’énergie noire et vaut 0.73.

[3] Les astrophysiciens aiment quantifier cela avec ce qu’ils appellent ‘z’. On a la relation \(z = \lambda_{obs} / \lambda_{emis} – 1\)