La vidéo du jour traite du problème des galaxies « impossiblement précoces » découvertes par le télescope James Webb. Est-ce qu’elles mettent à mal la théorie du Big-Bang ?
Voici comme toujours quelques commentaires et références pour les plus curieuses.
La fonction de masse des halos
Un élément central dans l’argument qui nous fait dire que ces galaxies sont improbables, ce sont ces courbes qui donnent l’abondane attendue des halos de matière noire en fonction de leur masse et du redshift. Ce qu’on appelle la fonction de masse des halos.
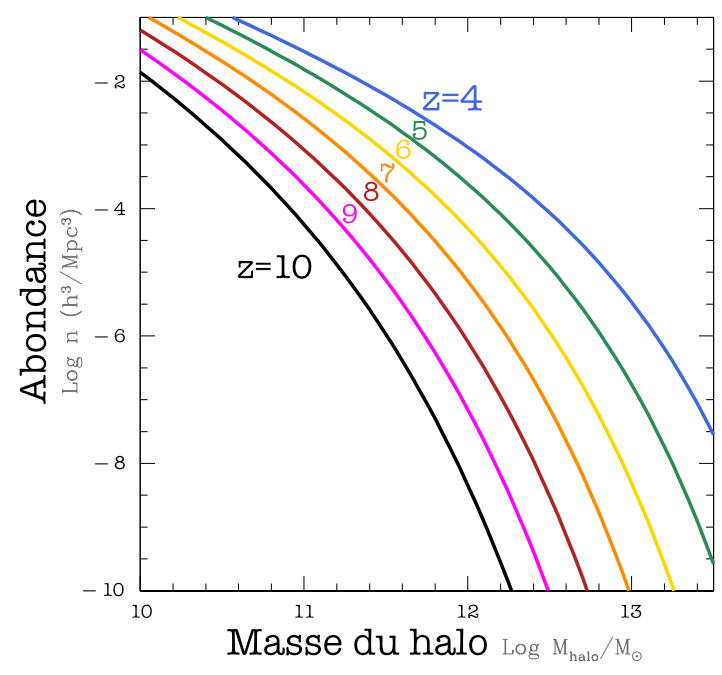
J’ai adapté cette figure de la publication :
Steinhardt, C. L., Capak, P., Masters, D., & Speagle, J. S. (2016). The impossibly early galaxy problem. The Astrophysical Journal, 824(1), 21.
Elle nous montre la densité en nombre des halos de matière noire (combien de halos dans un volume donné exprimé en \(\mathrm{MPc}^3\).) en fonction de la masse et pour différents redshift. Ici c’est une fonction cumulée, donc ça donne le nombre de halos ayant une masse au moins X dans un volume donné.
On parle ici de la masse des halos de matière noire, puisqu’on sait que les galaxies se forment au sein de ces halos, et que la fraction baryonique est de l’ordre de 20%. Sachant dans la matière baryonique, tout ne devient pas de la masse stellaire, ça veut dire que pour un halo donné la masse stellaire sera typiquement de moins de 10% de la masse du halo.
Si on prend par exemple une masse de halo de 1000 milliards de masses solaires (ce qui pourrait donner potentiellement une galaxie de la masse stellaire de la nôtre), on voit qu’elles sont très peu probables à redshift 10, mais que la probabilité augmente de plusieurs ordres de grandeur quand le temps passe (et que le redshift diminue).
Ces courbes s’obtiennent à partir d’un formalisme de calcul qui considère les fluctuations de densité de matière initiales et les fait évoluer au cours de l’expansion de l’Univers pour prédire la fonction de masse des halos. On peut citer le formalisme de Press-Schechter, qui a été depuis amélioré pour donner celui de Sheth-Tormen. Ces formalismes sont semi-analytiques mais ont un certains nombres de paramètres libres qui doivent être déterminés.
Le break de Balmer
Je suis toujours un peu embêté quand j’utilise des termes scientifiques un peu spécifiques, car bien souvent ils n’existent vraiment qu’en anglais. Je me suis résolu à utiliser le terme de break puisque c’est celui qu’on trouve en général dans les publications (mais j’ai trouvé une thèse en français qui parlait de cassure).
Revenons sur le mécanisme à l’oeuvre. Voici un des spectres que je montrais dans la vidéo
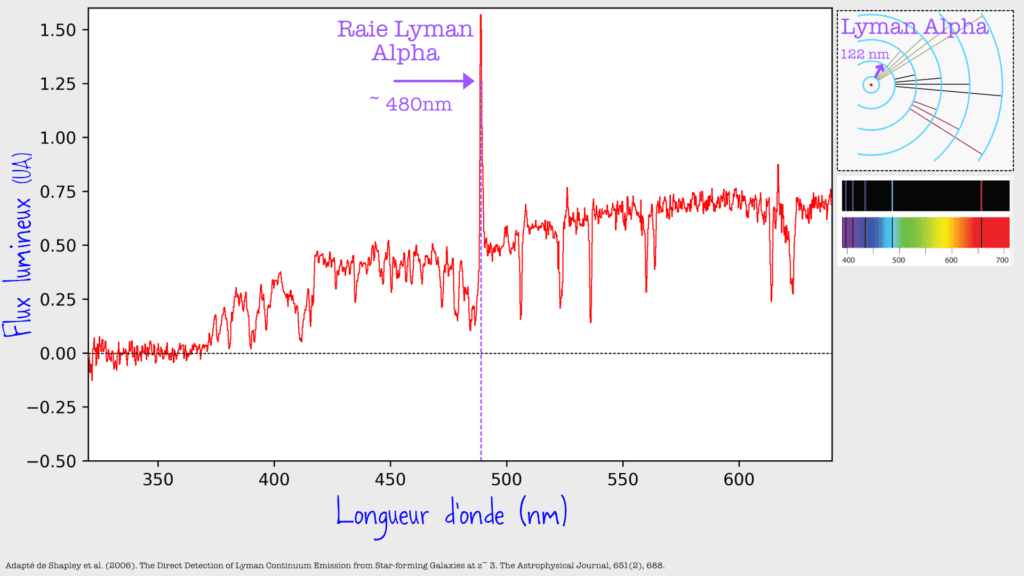
Et avant de parler du break de Balmer, parlons du break de Lyman ! C’est le fait qu’en-deça de 370nm environ sur la figure ci-dessus, il n’y a essentiellement plus de signal. Mais pourquoi ?
Quand un atome d’hydrogène est dans l’état fondamental (n=1), il peut absorber de la lumière à différentes longueurs d’ondes. Ce sont les raies de Lyman qui sont dans l’UV (ici données en Angström)
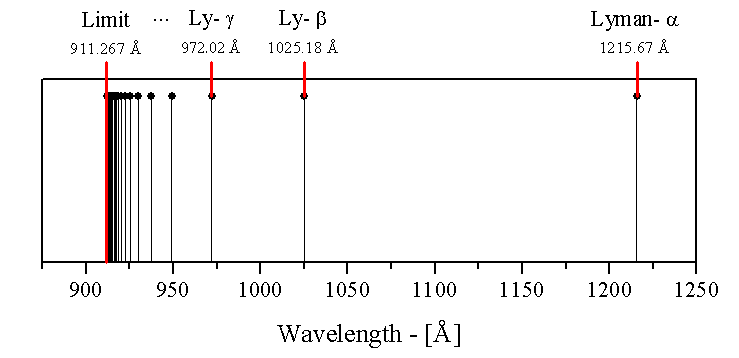
De droite à gauche : on voit que la raie alpha est vers 122 nm, la beta vers 103 nm, la gamma vers 97 nm, etc. Et surtout on voit que l’écart entre les raies se resserre car les niveaux d’énergie élevés sont proches les uns des autres. Asymptotiquement, la limite de 91nm environ correspond à l’énergie d’ionisation : le fait d’arracher complètement l’électron du niveau 1. C’est-à-cette valeur que ce trouve le break de Lyman. Mais pourquoi ça n’est pas une simple raie d’absorption ?
Si un photon a une longueur d’onde de 122nm, il peut faire passer l’électron du niveau 1 au niveau 2. Mais s’il a une longueur d’onde de 100nm, il est trop énergétique pour le faire passer au niveau 2 mais pas assez pour le niveau 3. On pourrait se dire que « trop énergétique » ne devrait pas poser de problème puisque « qui peut le plus peut le moins ». Sauf que l’énergie se conserve, et qu’il faut bien que le surplus d’énergie aille quelque part, et là il n’aurait nulle part où aller. Donc pour les transitions de niveaux énergétiques, on a bien des raies d’absorption.
Mais quand on atteint l’énergie d’ionisation, c’est différent ! Une fois l’électron arraché, toute l’énergie supplémentaire peut aller dans son énergie cinétique. C’est le principe de l’équation d’Einstein pour l’effet photoélectrique.
Et donc toutes les longueurs d’ondes au-delà de la limite de Lyman sont susceptibles d’être absorbées, d’où la présence de cette cassure dans le spectre. Dans mon spectre au-dessus, vu que j’avais un redshift de 3, elle se trouve à environ 4 fois la longueur d’onde d’ionisation, vers 360 nm donc.
Alors tout ça c’était pour Lyman, c’est à dire quand on part d’un atome dans l’état fondamental. Mais le même raisonnement s’applique pour un atome dans l’état n=2, et qui donne naissance aux raies de Balmer, qui nous sont plus familières puisqu’elles sont dans le visible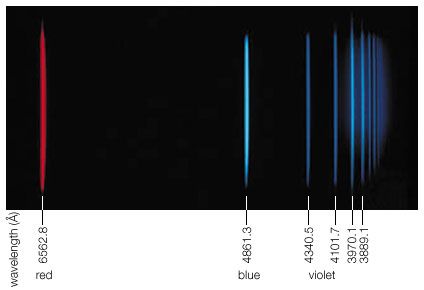
(Ici elles sont représentées en raies d’émissions mais l’idée est la même). Et on retrouve une accumulation asymptotique vers 365nm qui correspond à l’ionisation pour un électron initialement dans l’état n=2. Donc on s’attend aussi à un break pour toutes les longueurs d’ondes inférieures à 365 nm (multiplié par (1+z) avec le redshift). Mais attention l’effet sera moins violent que le break de Lyman !
En effet pour que l’absorption ait lieu, il faut que l’atome soit dans le niveau n=2, ce qui est potentiellement plus rare que d’être dans l’état fondamental. La présence et la taille de la cassure va donc dépendre de la quantité d’atomes d’hydrogène présent dans ce niveau, qui lui même est relié à la température des étoiles.
Il se trouve que l’effet est le plus fort pour les étoiles de type A, c’est-à-dire environ 2 masses solaires et une température de 8000 à 10000K. Pour les étoiles moins lumineuses, il y a moins d’atomes dans le niveau 2 car ils sont dans le niveau 1. Inversement pour les étoiles plus lumineuses, les atomes d’hydrogènes seront plus fréquemment dans des états d’énergie supérieure.
Et c’est en ça que l’intensité du break de Balmer d’une galaxie nous renseigne sur sa composition en étoiles (et donc sur la façon dont cette distribution a évolué depuis la naissance de la galaxie).
D’autres solutions au problème des galaxies impossiblement précoces ?
Je l’ai brièvement évoqué dans la vidéo, mais une solution au problème des galaxies précoces pourrait résider dans l’hypothèse que l’on prend sur la fonction de masse des étoiles, c’est-à-dire la distribution de masse lors de la formation de la galaxie. L’histoire ressemble à ce que je racontais sur la fonction de masse des halos. A partir des galaxies autour de nous, on a inféré une sorte de distribution universelle qui semble coller tout le temps
Il en existe plusieurs variantes analytiques (voir Wikipédia)
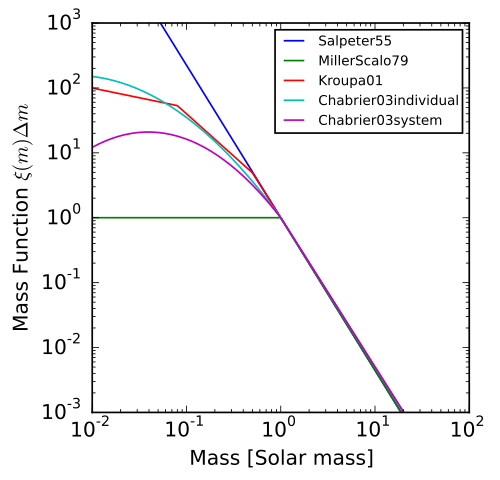
Une des publications récentes que j’ai mentionné dans la vidéo examine l’hypothèse selon laquelle ces distributions ne seraient pas applicables telles qu’elles aux galaxies très précoces, et notamment parce qu’à cette époque le rayonnement fossile avait une température dont on ne pouvait pas négliger l’impact. C’est l’hypothèse des « hot Initial Mass Function » qui semble résoudre la tension.
Steinhardt, C. L., Kokorev, V., Rusakov, V., Garcia, E., & Sneppen, A. (2023). Templates for Fitting Photometry of Ultra-High-Redshift Galaxies. The Astrophysical Journal Letters, 951(2), L40.
On peut citer aussi une simulation plus récente qui aboutit à une conclusion analogue
McCaffrey, J., Hardin, S., Wise, J., & Regan, J. (2023). No Tension: JWST Galaxies at $ z> 10$ Consistent with Cosmological Simulations. arXiv preprint arXiv:2304.13755.





19 Comments
Bonjour,
Je me demandais si, pour le calcul de la distance en fonction du redshift, on tenait compte de la modification (éventuelle) de la vitesse d’éloignement (qui dépends de la métrique de l’univers si j’ai bien suivis vos autres vidéos) pendant le parcours des photons?
En effet, si la vitesse relative d’éloignement était plus rapide au début du trajet du photons et bien moins à la fin, est-ce que ça ne fausserait pas la mesure de la distance de la galaxie?
Oui en effet en principe pour calculer le redshift, il faut faire une intégrale des composantes de la métrique sur l’ensemble du chemin suivi. Dans le cas simple d’une métrique Robertson-Walker on sait le faire analytiquement
https://en.wikipedia.org/wiki/Redshift#Mathematical_derivation
Mais on pourrait imaginer une métrique plus compliquée et écrire l’intégrale
Ok, ma question n’était donc pas stupide! 😅
Par contre, y’a-t-il un moyen de connaitre la métrique au cours du temps ? J’imagine que non, mais les astronomes sont tellement ingénieux…
Sinon, on doit postuler que la métrique suis une loi simple et est homogène partout (ce qui semble raisonnable)?
En effet on postule que la métrique a une certaine forme liée à des hypothèses raisonnables, et on estime les paramètres libres (par exemple la répartition matière ordinaire/noire ou la valeur de la constante cosmologique)
Bonjour !
Voici les quelques questions que je me suis posé pendant le visionnage de votre vidéo:
– Est-ce que dans un cas comme celui-ci, de nouvelles observations avec NIRSpec devient-elle prioritaire sur d’autres mesures déjà programmées, doivent-elles faire l’objet de nouvelles demandes de temps d’observation, ou entrent-elles dans la liste d’attente, comme toutes les autres demandes de temps de mesure déjà acceptées ?
– Sauf erreur, en astrophysique, le « sigma » est de 3 (au lieu de 5 en physique des particules). Qu’est-ce que cela implique, concrètement, au niveau du nombre d’observations et/ou des incertitudes ?
– Je ne sais pas s’il s’agit d’une hypothèse ou d’un fait, mais il aurait existé, au sein du tout jeune univers, des étoiles hyper-massives (ordre de grandeur 10^4 à 10^5 masse solaire). A-t-on une idée du ratio luminosité / masse de ces étoiles, qui pourrait donner des informations sur la masse de ces anciennes galaxies. Ou alors, compte-t-on justement sur la mesure de la masse de ces galaxies pour estimer la masse et le type de ces premières étoiles ?
Merci.
Non je ne pense pas qu’il y ait de notion de priorité. A mon avis les cycles normaux de demande s’appliquent, par contre il est sans doute certains que ces demandes là seront approuvées.
Sur les incertitudes, on est dans un cas un peu moins clair qu’en physique des particules. Pour les particules, on a un truc clair à mesurer, on a les valeurs de « background » attendues selon le modèle standard et donc une notion assez formalisée de « anomalie au delà de X sigmas ».
Ici ça me parait moins clair.
Juste un petit coucou pour te remercier de ta réponse sur YT et du boulot monstre que tu fais 🙂
Sans elle je n’aurai pas eu l’idée de double check ce que j’avançais alors que j’aurai pu au moins vérifier les compléments d’infos du billet, tout y étais ! ^^’ J’avais également trouvé le dernier article que tu cites; arXiv:2304.13755. grâce à la chaîne d’Anton Petrov, il fait des vidéos courtes quotidiennement sur un papier scientifique récent et si tu ne le connaissait pas déjà je ne peux que t’inviter à y jeter un coup d’œil, cela pourrait peut-être même te donner des idées de vidéos qui sait ! Encore merci !
J’ai posté sous la vidéo, mais ça aura probablement plus de chance d’être lu ici 😉
Je suis spécialiste d’évolution des galaxies et je dois dire que je suis impressionné par la qualité ce cette vidéo, qui explique avec une grande clarté les limites actuelles de nos observations. David, tu fais vraiment un travail incroyable de vulgarisation, très haut dessus de la communication tapageuse qu’on voit passer trop souvent par l’enchaînement devenu trop classique: article assez survendu, communiqué de presse qui en remet trois couche, reprise dans la presse sans plus aucune précaution.
Un grand merci pour expliquer si bien ce qu’il se passe en vrai dans notre démarche de tous les jours. Digérer les résultats sur les galaxies massives dans l’Univers jeune de JWST (et EUCLID qui arrive) va prendre beaucoup de temps et de débat. Je mettrais bien une piécette sur l’atténuation de la lumière par la poussière qu’on a peut-être mal compris dans ces objets, mais je suis biaisé!
Merci pour ce sympathique témoignage !!
Bonjour !
Mes travaux laissent à penser que la matière est apparue subitement en un seul bloc d’une multitude de neutrons à l’instant suivant l’inflation. Une telle circonstances peut expliquer la venue précoce d’étoiles massives, de trous noirs et de grandes galaxies.
Bonjour, je me demandais, quelle est la proportion de physiciens qui ne croient pas à la théorie du Big Bang ?
0%.
Et pour répéter ce que je dis souvent, pour un physicien le Big-Bang c’est : l’Univers a été, dans le passé, dans un état extrêmement dense et extrêmement chaud.
Ah, d’accord, donc ce n’est même pas des personnes qui disent cela à partir d’une très faible minorité, c’est de l’invention et du mensonge pur.
Honteux.
Merci de votre réponse et de vos vidéos !
Je me risque à une spéculation: si la matière noire évolue dans une ou plusieurs dimensions supplémentaires, nous ne pourrions voir que les projections de ses effets sur notre espace-temps à 3 + 1 dimensions. Les halos pourraient être une telle projection sans que nous puissions en observer les causes ou les propriétés. Cela compliquerait singulièrement notre compréhension de l’univers si lors du big bang, les baryons, leptons et autres bosons étaient les seuls à avoir droit de cité dans nos quelques dimensions d’espace-temps. D’autres dimensions accueilleraient des particules exotiques.
Bonjour David,
Encore une vidéo exceptionnelle qui donne un éclairage très pertinent sur la situation ! J’avais lu quelques papiers sur le sujet depuis les observations du James Webb et vu une vidéo de conférence scientifique. Mais j’avais encore un peu de mal à saisir en détail toutes les subtilités du problème, ce qui est maintenant fait grâce à toi. Tu m’as permis de recoller les morceaux et organiser le schéma mental du problème pour aider ma mémoire à long-terme 😉
Je n’avais pas connaissance de l’utilisation du break de Balmer pour déterminer la composition stellaire des galaxies et le complément que tu as apporté ici sur le blog m’a vraiment bien fait comprendre le principe.
Sinon pendant la vidéo, je me faisais la réflexion que l’hypothèse sur la distribution de masse à la formation des galaxies avait de forte chance d’être biaisée dans le contexte de l’univers primordial. Finalement j’avais bien intuité au vu de la fin de ton billet. Je vais essayer de prendre le temps de lire les deux articles que tu cites. Merci encore !
Après avoir lu l’article (Steinhardt, C. L., Kokorev, V., Rusakov, V., Garcia, E., & Sneppen, A. (2023). Templates for Fitting Photometry of Ultra-High-Redshift Galaxies. The Astrophysical Journal Letters, 951(2), L40.), je me pose la question de la nature physique du « halo collapse » qui y est mentionné. Je comprends que l’IMF est dérivée des observations au z faible <3. Mais quelle est la physique à l’œuvre sachant que les halos sont en grande partie constitués de matière noire inconnue? Comme le dit l’article il est inévitable qu’inférer quantitativement la genèse des galaxies, d’observations à z faible se heurte à un problème à z élevé.
Les conclusions de l’article sont très intéressantes et proposent trois perspectives:
– révision de l’IMF sur la base des observations à z élevé en intégrant plus de paramètres que la seule luminosité
– nouvelle physique des particules pour comprendre la nature du « halo collapse »
– révision de la physique de formation des étoiles éventuellement en avance du « halo collapse »
Plus que la remise en cause du big bang, il me semble que l’enjeu est avant tout de comprendre la matière noire puisque la concentration baryonique (les galaxies, amas, superamas, etc) lui semble intimement liée. Et encore il restera le plus gros morceau, la question de l’énergie noire (pression négative responsable de l’expansion) soit 70% de l’énergie de l’univers. Si ces 95% d’énergie inconnue sont issus du big bang, la compréhension de leur nature amènera sûrement des clés pour mieux comprendre le big bang lui même sachant que notre monde baryonique (4,5%) est ultra minoritaire.
Bonjour,
Je suis étonné de voir comment on conçoit l’univers. J’ai toujours l’impression que l’on cantonne toutes les théories cosmologiques à ce que nous sommes capables de détecter. Est-il pertinent d’imaginer qu’au delà de notre champ de détection au sens large, il existe d’autres développements de l’univers qui ne se matérialiserait pas par une expansion mais une rétraction par exemple avec des ensembles de galaxies qui serait tellement éloignés de nous que ces ensembles seraient indétectables pour nous ? Ces mêmes ensembles très éloignés pourraient également faire partie d’ensembles beaucoup grands indétectables pour nous etc … Tout ca pour dire que le modèle actuel d’un univers en expansion à partir d’une singularité unique, ne me parait pas plus satisfaisant que le modèle d’une terre plate à l’âge féodal alors que la vue que nous avions au bord des océans était limitée ou même celui d’une terre qui serait le centre de l’univers. Peut être me manque t-il des connaissances pour accepter un univers unique et uniforme ? Existe-t-il des arguments pour le prouver ou est-il possible au contraire que notre univers ne soit pas aussi simple. La partie que nous observons ne pourrait-elle pas se comporter comme une étoile qui exploserait dans un espace infini ou en tout cas beaucoup plus grand ?
super !