Ca fait longtemps que je voulais parler des méthodes de détection des exoplanètes. La vidéo est un peu longue, mais il y a plein de trucs à raconter !
Et comme j’ai dû couper dans le script pour éviter de trop dépasser, voici quelques compléments plus pointus sur chacune des méthodes.
Détection directe
Une petite justification concernant mon calcul de contraste, on peut le prendre de différentes façon. On sait que le Soleil a une puissance d’environ \(4.10^{26}\) Watts. Peut-on estimer la puissance lumineuse de la Terre dans le visible ? J’ai fait de la façon suivante : on sait que la Terre reçoit environ 1400 W/m2 du Soleil, dont elle réfléchit environ 30% (l’albedo), donc on va dire dans les 400W/m2. Si on multiplie grassement par la surface de la Terre, on trouve environ \(2.10^{17}\) W. On a un bon ratio d’un milliard avec la puissance du Soleil, et encore il faudrait prendre en compte la géométrie (toute la Terre n’est pas éclairée, et pas sous incidence normale) et au moins mettre un facteur 4 en plus. Mais ça donne l’ordre de grandeur.
La raison qui fait que ça se passe mieux en infrarouge (et notamment en infrarouge moyen, disons autour de 5 microns), c’est à cause du spectre de corps noir respectivement du Soleil à ~6000K et de la Terre à ~285K.
Parmi les résultats amusants, on peut citer l’étoile HR8799 qui abrite 4 exoplanètes visibles par détection directe. Voici un petit GIF où on voit bien la zone masquée par le coronographe, et les 4 exoplanètes en orbite, à partir d’images prises sur 7 ans à l’observatoire Keck à Hawaï. Ca a été imagé à une longueur d’onde de 3.5 microns.
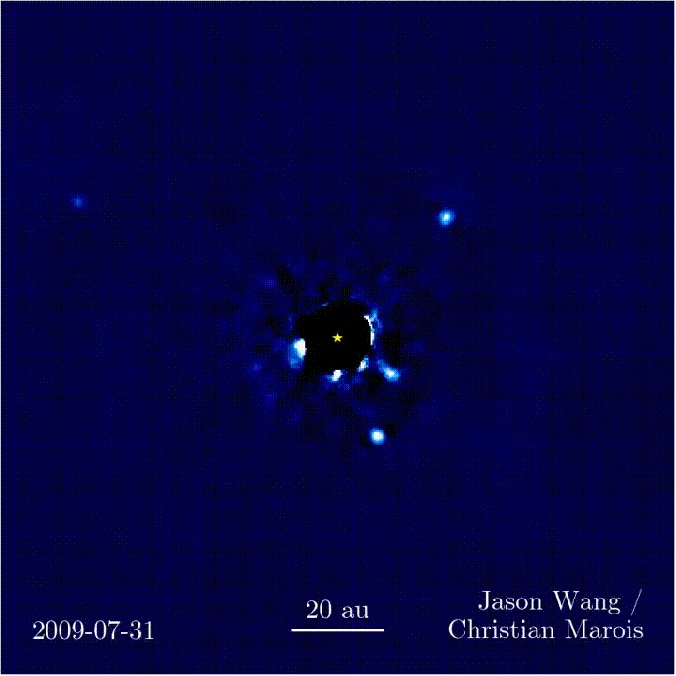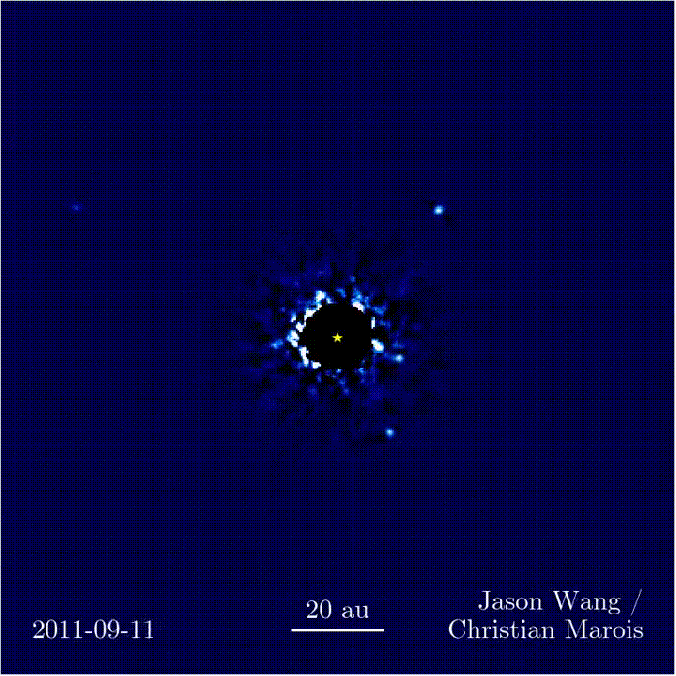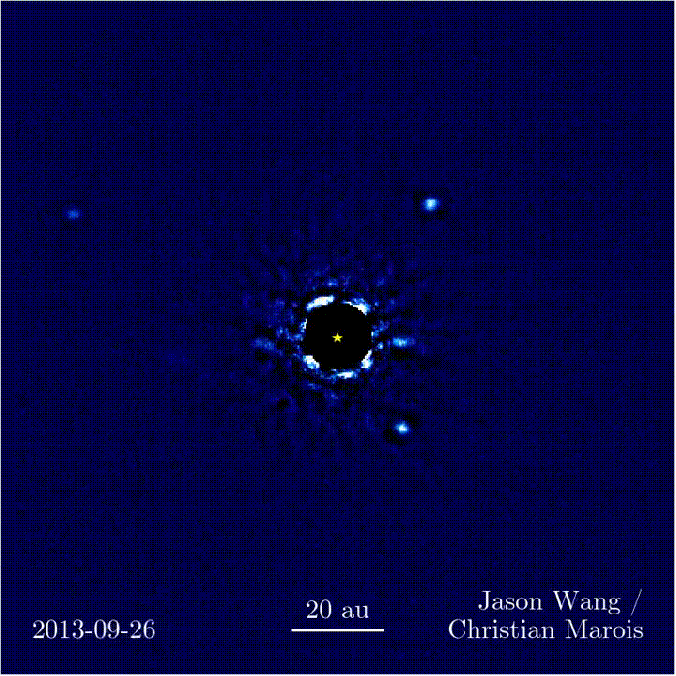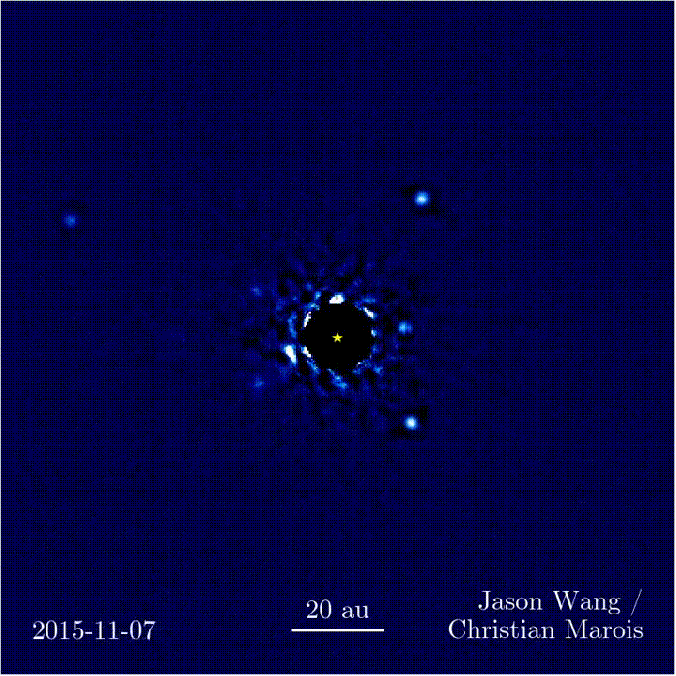
Transit
Pour la méthode du transit, quelques précisions avec un peu de formules. La chute de luminosité (en %) est simplement reliée au rapport des surfaces, donc des rayons au carré
\(\left(\frac{R_P}{R_S}\right)^2\)
Pour la probabilité d’être dans la bonne direction pour détecter une présence par transit, c’est en gros le rayon de l’étoile divisé par le demi-grand axe
\(\frac{R_S}{a}\)
Une petite précision importante sur la façon dont on arrive à tirer des informations de tout ça (et s’applique pour toutes les méthodes). Une relation importante à avoir en tête, c’est la troisième loi de Kepler, qui relie la période de révolution et le demi grand axe
\(\frac{a^3}{T^2} = \frac{GM_S}{4\pi^2}\)
Donc quand on connait l’un (période ou demi grand-axe), on connait l’autre. Sauf que là vous allez me dire : il faut connaitre la masse de l’étoile ! Heureusement on peut assez bien l’estimer à partir de sa luminosité. Il existe des relations simples entre masse et luminosité (pour les étoiles de la séquence principale du moins), de la forme
\(L \propto M^{\alpha}\)
où \(\alpha\) est un exposant qui vaut typiquement 3.5-4. Donc on arrive assez bien à estimer les masses des étoiles concernées.
Astrométrie
Pour l’astrométrie, j’ai peut-être trop laissé sous-entendre qu’on cherchait à voir des oscillations de trajectoire nettes. En réalité une étoile n’est jamais « un » pixel de l’image qui bouge, mais elle est étalée sur plusieurs pixels, c’est une tâche. En fonction des intensités respectives, on calcule la position du « centre photométrique », c’est à dire le centre de la tâche. Quand l’étoile bouge, le centre photométrique se déplace, même si visuellement on peut avoir l’impression que rien n’a bougé. Cette méthode permet d’avoir accès à des déplacements inférieurs à la taille du pixel.
Vitesses radiales
Il faut que je précise plusieurs choses pour les vitesses radiales. Comme je l’ai dit, ce qu’on estime n’est pas la masse de la planète, mais va dépendre de l’angle d’inclinaison \(i\), où \(i=0\) correspond à une orbite perpendiculaire à l’axe de visée. En pratique ce qu’on détermine en mesurant l’amplitude d’oscillation de la vitesse radiale, c’est \(M\sin i\).
La manière de le faire, c’est d’utiliser ce qu’on appelle la fonction de masse du système binaire \(f\). Elle permet de relier les masses du système binaire et l’amplitude de vitesse K mesurée par effet Doppler
\(\frac{T K^3}{2\pi G} = f = \frac{(M_2 \sin i)^3}{(M1+M2)^2}\).
Si la masse de l’étoile \(M_1\) est très supérieure à \(M_2\), on voit qu’on a essentiellement
\(M_2 \sin i =\left( \frac{T K^3 M_1^2}{2\pi G}\right)^{1/3}\)
et on peut déduire (au mieux) \(M_2 \sin i\).
Microlentilles
Un truc que j’ai toujours du mal à bien faire passer quand on parle de microlentilles , c’est le fait que le phénomène existe même si la masse ne passe pas PILE entre l’observateur et l’étoile. On définit une notion de paramètre d’impact, qui est la distance minimale entre les deux lors du passage, et on peut calculer la forme du pic en fonction de ça.
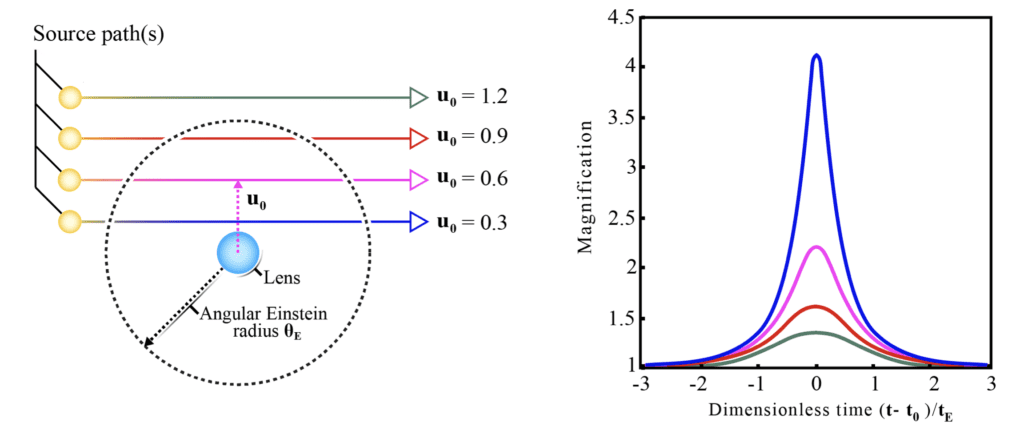
(Fun fact : c’était l’objet de mon stage de license de rechercher des événements de ce genre, pour essayer de détecter de la matière noire à partir de phénomènes de microlentilles)
Par contre pour les caustiques, ça devient vite compliqué. En fonction de la distance angulaire à l’étoile, on peut avoir des courbes plus ou moins exotiques
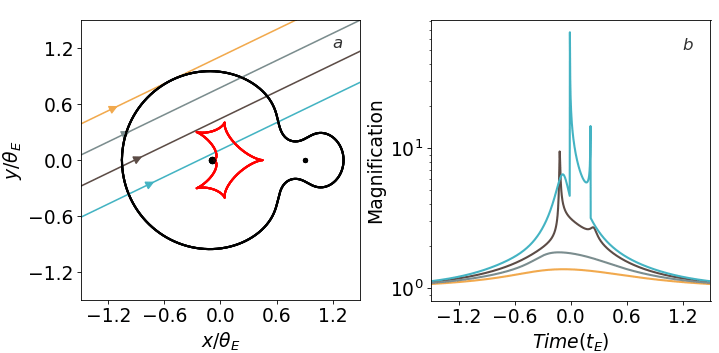
Quand on recherche des événements, on peut utiliser un paramètre qu’on appelle « la profondeur optique ». C’est un nombre sans dimension qui indique en gros la probabilité qu’une étoile donnée à un instant donnée soit en train de subir un phénomène de microlentille. Cela est directement relié à la densité des objets suceptibles de provovuqer le phénomène, dans la direction d’observation. C’est pour ça qu’on regarde vers le bulbe galactique, pour lequel la profondeur optique est d’environ \(10^{-6}\). Donc si vous regardez une étoile dans cette direction, il y a une chance sur un million qu’elle soit en train de subir le phénomène.

8 Comments
Salut !
Bon boulot comme d’hab !
J’ai cité ta chaîne Youtube sur ma page démontrant la non-existence des singularités des trous noirs https://horizongravitation.virtualhost2.workers.dev/
Continue comme ça !
SEPT !!
je croyais connaitre assez correctement le sujet…
BIN-NON… MERCI DAVID
Bonjour, si vous connaissez un peu le sujet… petite question :
Dans le diagramme masse/distance étoile, aucune des 2000 exoplanetes n’est à la fois plus éloignée de son étoile ET de masse plus faible que la terre ?! (Quadrant haut/gauche vide)
C’est normal que la terre ne soit pas au centre du nuage de points, mais de là à se trouver à une limite ?
David Louapre ne souligne pas vraiment ce point, ni que la cause serait nos méthodes de recherche. Sachant tout de même qu’il y en a 7 différentes… et que l’on peut détecter des exoplanètes de masse plus faible et aussi d’autres de trouvant plus loin de leur étoile… ce serait donc celles combinant les 2 qui passeraient sous le radar de nos 7 méthodes ?! Ce n’est pas intuitif et mériterait d’être souligné.
Ou bien la terre est exceptionnelle avec ces caractéristiques… et ça serait encore plus à souligner ! 😊
Merci pour vos éléments !
Faute d’orthographe : « provovuqer » 😉
Et « licence »
Super comme d’habitude.
J’aime bien ce format un peu plus long.
Moi aussi, j’ai appris plein de trucs, je croyais qu’il n’existait que 2 ou 3 méthodes.
Merci encore
Merci encore pour ces vidéos !
Une question : dans le diagramme masse/distance étoile, aucune exoplanete à la fois plus éloignée de son étoile ET de masse plus faible que la terre ?! (Quadrant haut/gauche)
Bugg sur mon commentaire initial, donc je fais court ici 🙂 , merci pour les détails !