Comme vous l’aurez deviné, le sujet du jour est la suite de celui d’il y a 2 semaines. Un sujet en pleine résonance avec l’actualité vénusienne récente, mais ça n’était pas calculé !
Une petite anecdote
Pour commencer, je voudrais vous raconter une petite anecdote amusante concernant la genèse (et l’avenir) de cette vidéo. J’ai découvert les travaux de Stuart Bartlett en écoutant son interview dans le podcast Mindscape de Sean Carroll (que je vous recommande). Il y parlait notamment de son concept de «lyfe», ainsi que de ses travaux sur le modèle de réaction-diffusion de Gray-Scott, et ça m’a tout de suite intrigué !
J’ai été lire ses publications et sa thèse [1], et j’ai trouvé ça fascinant. Je lui ai donc écrit pour savoir s’il pouvait me passer les vidéos de ses simulations pour que je les intègre à ma vidéo. Il m’a répondu fort sympathiquement et me les a envoyées… Et puis j’ai voulu les reproduire moi-même, en utilisant une technique de simulation assez différente de la sienne. Et là ça a fonctionné très bien, extrêmement bien même !
Je lui ai alors envoyé quelques vidéos de mes propres simulations, et là il m’a répondu que ma simulation était « amazing » et « definitely much faster than mine »…et il m’a proposé de travailler avec lui sur l’intégration de nouvelles idées dans cette simulation, pour essayer de trouver et modéliser un système ayant les 4 piliers de la « lyfe ». Me voici donc (de façon totalement inattendue !) embarqué dans un projet de recherche avec lui sur le sujet ! Il est probable que ça ne donne rien, ça reste de la recherche, mais c’est cool !
Passons maintenant aux détails scientifiques !
LYFE
Dans le papier de Bartlett et Wong où ils ont proposé le concept de «lyfe», il y a un diagramme intéressant que j’ai hésité à reproduire. C’est un diagramme de Venn où l’on voit les 4 piliers qu’ils ont considérés, et ce qu’on trouve aux différentes intersections.
Il est notamment intéressant de regarder les cas où l’on en a 2 ou 3 sur 4. Il y a le cas du modèle de Gray-Scott homéostatique (à qui il manque l’apprentissage), et dont j’ai parlé, mais les autres exemples sont instructifs.
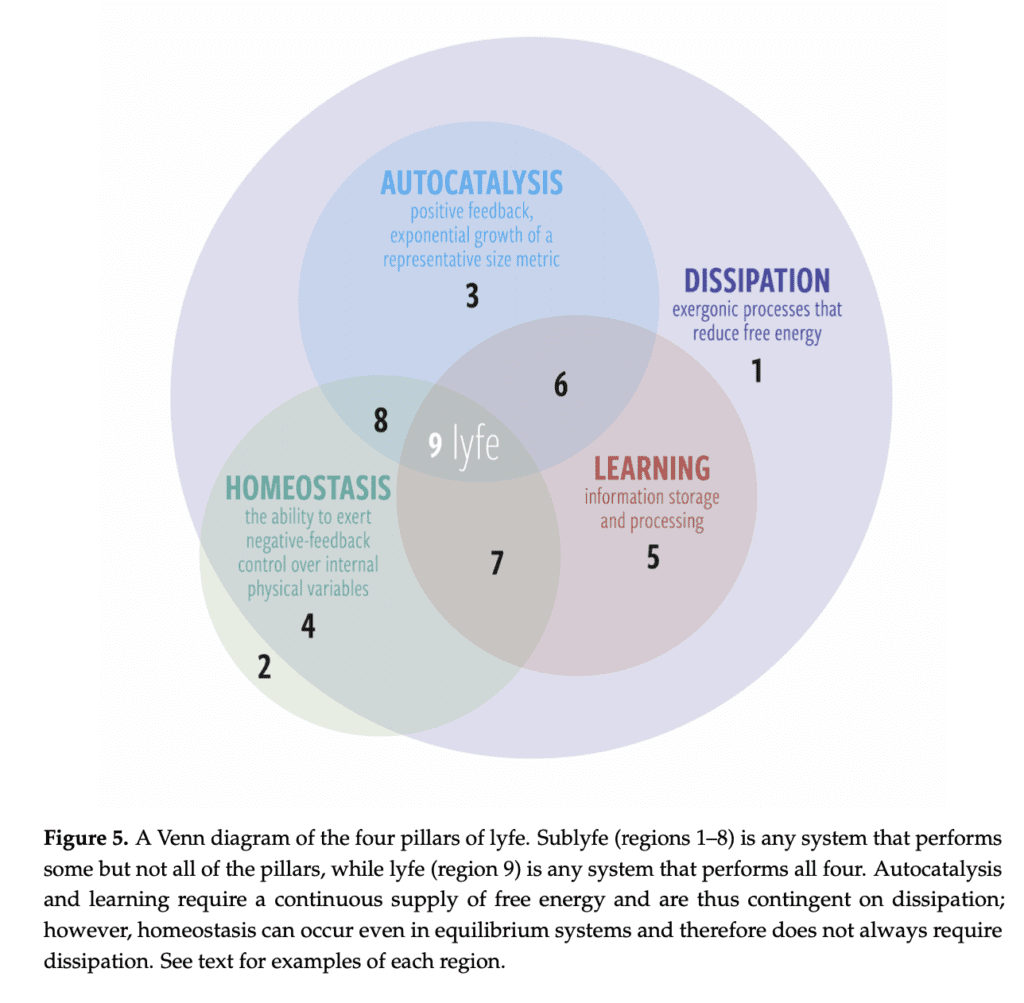
Le modèle de Gray-Scott homéostatique serait donc en (8). Un feu de forêt en (3). En (4) on peut avoir un oscillateur harmonique amorti (qui dissipe et régule sa position, mais n’a pas d’auto-analyse). Etc.
L’entropie, satané concept
Une fois de plus j’ai parlé de l’entropie, et une fois de plus je m’en suis sorti par une pirouette pour ne pas avoir à rentrer dans les détails. Je ferai peut-être un jour une « vraie » vidéo sur l’entropie. En attendant Passe-Science en a fait une, et je crois savoir que ScienceClic en prépare une !
Ma pirouette (qui consiste à dire que en gros l’entropie c’est l’énergie thermique) ne fonctionne évidemment pas si on y regarde de plus près, et le lien avec les notions de désordre n’y est pas franchement clair. Pour voir la faille, il suffit de prendre l’exemple usuel de deux blocs de métal à deux températures différentes (une « chaude » et une « froide ») que l’on met en contact et dont la température s’uniformise. Les seuls transferts sont des transferts de chaleur, et pourtant l’entropie augmente.
Pour ceux qui connaissent, cela vient évidemment du fait qu’on définit l’entropie avec \(dS = \delta Q / T\). L’entropie ça n’est donc pas « vraiment » le contenu en énergie thermique. Mais quand on ne veut pas rentrer dans les détails, je trouve que cette pirouette fonctionne plutôt bien.
De façon générale, mes explications ne rendent pas bien compte non plus de pourquoi la dilution d’une goutte d’encre serait une augmentation d’entropie dans la mesure où il n’y a pas d’échanges de chaleur dans l’affaire. De façon générale, j’aurai du évoquer l’idée de « dissiper des gradients », mais j’ai trouvé que ça nous aurait emmené un peu loin.
Une chose qu’il faut garder en tête, c’est que la thermodynamique « hors-équilibre » reste une discipline relativement jeune, et encore mal comprise. Notamment quand on est « loin » de l’équilibre (il y a des résultats plus riches quand on est sur des perturbations linéaires autour de l’équilibre). Pour ceux que ça intéresse, la lecture Nobel de Prigogine [2] est pas mal sur le sujet.
Rayleigh-Benard dans ma soupe
Pour illustrer la convection de Rayleigh-Benard, j’ai essayé de faire moi-même une petite manipe dans ma cuisine. J’ai d’abord essayé avec de l’eau, puis de l’huile, et différents additifs pour tracer le mouvement (épices diverses, sable coloré). Et puis je suis tombé sur une publication disant que l’idéal, c’était la soupe miso [3].
J’ai donc sorti la pâte miso de mon frigo, et en effet, ça marche très bien ! Comme vous avez pu le voir, on n’obtient pas des cellules hexagonales, mais le phénomène reste très visible.
Ah oui sinon autre astuce expérimentale : pour la diffusion de la goutte d’encre dans l’eau, j’ai pris de l’eau chaude, ça augmente le coefficient de diffusion !
Parlons chimie
Vous le savez, la chimie ça n’est pas mon fort. Et pourtant j’ai pris un certain plaisir à jouer avec les modélisations des cinétiques de réactions. J’ai fait plein de simplification : l’utilisation de seuils de combustion, l’ignorance (sélective) de la loi d’Arrhénius, le fait que les réactions ne soient pas explicitement équilibrées, les réactions irréversibles, etc.
Un petit point de méthode pour ceux qui seraient curieux des équations utilisées derrière. Considérons une réaction chimique simple du genre
A + B => C
Si la réaction est irréversible, l’avancement de la réaction va être proportionnel à \(k A B\), où \(k\) est une constante de réaction (qui peut dépendre de la température via Arrhénius), et on considère le produit des concentrations A et B.
Les équations différentielles qui traduisent l’augmentation ou la diminution des concentrations seront donc de la forme
$$\frac{dA}{dT} = – k A B$$
$$\frac{dC}{dT} = k A B$$
Un cas particulier de ça, c’est une réaction du genre
$$ S + A => S + B$$
Comme S apparait des deux côtés, sa concentration ne varie pas. Mais il s’agit bien d’une catalyse par S de la réaction A => B, et l’effet catalytique se retrouve alors reflété dans la cinétique, puisqu’on a
$$\frac{dB}{dt} = kAS$$
donc le taux de transformation de A en B est proportionnel à la concentration de S. Alors que pour une réaction simple A => B ça ne serait pas le cas.
Plein de réactions
Il y a plein de réactions autres que celle de Gray-Scott dont j’aurais pu parler : la fameuse réaction oscillante de Belousov-Zhabotinski (BZ), le système « Brusselator » de la bande à Prigogine, ou encore le système de Selkov [4], dont le modèle de Gray-Scott est un cas particulier, et qui est une modélisation un peu abstraite de la glycolyse.
Evidemment, il y a un thème très relié que j’ai savamment esquivé, probablement à la surprise de certains d’entre vous, ce sont les modèles de réaction-diffusion de Turing sur la morphogenèse. J’avoue qu’au départ c’était dans le script, et puis je me suis dit que ce serait trop long, trop lourd, et peut-être pas forcément très bien relié. Je pense que ce sujet mérite un traitement à part, donc il y aura sûrement un épisode dessus.
Ah d’ailleurs beaucoup ont logiquement pensé à cela quand ils ont vu mon teaser posté sur Facebook et Twitter. Et vous aurez peut-être été surpris de ne pas retrouver ces images-là dans la vidéo. C’est voulu ! Je ne voulais pas spoiler en montrant une vraie réaction de Gray-Scott, alors j’ai montré un truc un peu différent.

Ce que vous voyez sur l’image de ce genre est en fait le « diagramme de phase », obtenu quand on fait varier horizontalement et verticalement deux paramètres de la réaction de Gray-Scott (le taux d’approvisionnement de A et le taux de décroissance de B). Et suivant les valeurs de ces deux paramètres on n’obtient pas les mêmes motifs.
Une manière simple de faire le diagramme de phase, c’est de lancer une grosse simulation dans laquelle ces deux paramètres varient spatialement (horizontalement et verticalement). Et comme ça en une seule simulation on obtient tout le diagramme de phase ! C’est ce que représente l’image ci-dessus. On y voit donc
- une zone jaune uniforme où la réaction est trop importante et il y a plein de B,
- à l’opposé une zone noire où rien ne se passe,
- et entre les deux une région où l’on a soit des « cellules » soit des « tubules » (et même des cellules inversées à la frontière), ce qui est typiquement le genre de chose qu’on retrouve dans les modèles de Turing.
La différence entre les patterns de Turing et le modèle de Gray-Scott, c’est ici le caractère dynamique. Dans un modèle de Turing, les patterns émergent du bruit partout à la fois, ici on a l’effet de « colonisation ».
[1] Bartlett, S., & Wong, M. L. (2020). Defining Lyfe in the Universe: From Three Privileged Functions to Four Pillars. Life, 10(4), 42.
Why is Life? An Assessment of the Thermodynamic Properties of Dissipative, Pattern-forming Systems
[2] Ilya Prigogine, Nobel Lecture
[3] Cellules de Bénard dans la soupe miso et dans la couche limite atmosphérique Olivier Boucher1, Marie Doutriaux-Boucher






70 Comments
Merci pour cette inspirante vidéo. Tes coding skills ne sont plus à démontrer avec le compliment de Stuart Barlett!
Tu écris dA/dT=-kAB
mais juste après: dB/dt=kAS
voulais tu écrire dA/dt=-kAB ? (note le t ou le T)
Comment as-tu choisis le coefficient de dissipation de B? (Et d’apparition de A)
Peut on avoir des résultats intéressants lorsqu’ils varient en fonction de la température?
Merci encore, bonne continuation. Super projet, ça donne envie de faire des simu.
Après l’équation n’est pas la même car j’ai illustré une autre réaction A + S => B + S
Sion pour le choix des coefficients, comme le montre le diagramme de phase, il faut les choisir pour qu’on soit dans la zone qui donne des cellules (plutôt que des tubules ou bien les zones qui ne donnent rien)
Bonjour, La vidéo était très intéressante ! Je commence à m’intéresser à la modélisation de feu de forêt et je me demandais d’où venaient les equa diffs utilisées à 16:30 ? Merci beaucoup !
« J’avoue qu’au départ c’était dans le script, et puis je me suis dit que ce serait trop long »
> Et moi qui l’attendait comme un sot pendant la moitié de la vidéo…
« Je pense que ce sujet mérite un traitement à part, donc il y aura sûrement un épisode dessus. »
> Ouf, ça va alors, un mal pour deux biens
Bonjour, article très intéressant, comme toujours, merci pour votre travail!
Je tiens à vous partager les travaux de M. François Roddier qui agrémenteront agréablement peut-être quelques unes des notions développées à travers votre billet
https://www.francois-roddier.fr/
Envisageriez-vous éventuellement de rendre public vos codes afin que vos abonnés puissent s’amuser à lancer eux aussi chez eux vos superbes simulations?
Je vous souhaite une très bonne continuation!
> Envisageriez-vous éventuellement de rendre public vos codes afin que vos abonnés puissent s’amuser à lancer eux aussi chez eux vos superbes simulations?
Oh, je plussoie cette idée !!!
En attendant, il y a déja cela: https://www.youtube.com/watch?v=BV9ny785UNc
Je ne vais pas encore les publier tout de suite car je travaille encore dessus. J’utilise plusieurs techniques un peu retors pour accélérer, mais la base est très simple. En effet le lien YouTube me semble bien l’expliquer.
David
Bonjour,
Quel sujet passionnant! Moi qui touillais un peu avec qques pages web de simulation de développement avec mutation via automate cellulaire (un chouette exemple ici: https://thelifeengine.net).
Je regarde ces vidéos avec un peu de décalage (pas un addict à YT).
J’ai trouvé une implémentation en Python de la première partie de la simulation simple (réactifs A et B). Cela marche très bien et reproduit les ‘cellules’ obtenues. Lien ici: https://github.com/soilstack/react_diffuse
Bon, fort de cela, je voudrais ajouter A’ et B’, pour pouvoir ensuite implémenter le système double endothermique et exothermique, et jouer avec les variations de température du milieu.
Vous serait-il possible de revenir un peu là dessus et expliquer comment vous avez pris en compte la température (k et k’ sans doute fonction de t, et t modélisé à l’instar de la concentration d’un réactif diffusant?)?
Que représentez-vous dans la dernière simulation, les concentrations cumulées de B et B’? On ne voit pas véritablement de changement lorsque vous dites que la réaction exothermique prend le dessus. On le voit bien dans la visualisation des températures du milieu, mais les ‘cellules’ restent identiques…
Mille mercis en tout cas pour l’exceptionnel travail de présentation et de vulgarisation, tout en évitant les écueils courants rencontrés sur YT (langage, égo, montage etc). Continuez, c’est passionnant!!!
Bien à vous,
Grégoire
A toutes fins utiles, je me suis jeté à l’eau:
https://github.com/gregvds/grayscott
Voici ma version, en python3 avec Vispy pour l’accélération OpenGL. J’ai constaté récemment un souci avec PyQt5, je vous conseille PySide6 comme backend donc.
J’ai ajouté qques améliorations graphiques, comme des colormaps alternatives, du hillshading, et la possibilité de switcher entre les différents patterns de Pearsons, réinitialiser la modélisation, l’accélèrerer, changer la valeur de dD, et bien sur ajouter ou retirer du réactif catalyseur B (ou V selon la dénomination).
Voilà, si vous avez envie de vous amuser un petit peu avec le modèle de réaction-diffusion de Gray-Scott ;-).
Absolument, j’ai été bluffé par la richesse et agilité de pensée de François Roddier et la puissance de la discipline thermodynamique qui a encore beaucoup à nous apprendre je le pressens 😉. Il y a des années d’idées de recherche à puiser dans les billets et conférences de Roddier qui a fait une synthèse puissante sur beaucoup de phénomènes reliables à la thermodynamique . Une mine d’or à ne pas perdre je vous dis
Bonjour!
Merci pour cette vidéo et ces explications, le sujet est réellement fascinant. Ça fait un moment que l’idée d’essayer de créer une forme de vie informatique basique (très basique hein ^^), le concept de Lyfe va ajouter pas mal d’eau à mon moulin!
Du coup concernant les simulations, vu les échanges avec Stuart Bartlett, je suppose que les sources ne sont pas disponibles? Si ça n’est pas le cas, j’aimerais vraiment y avoir accès ^^
Je plussoie la demande de sources pour tenter des choses aussi ^^
A propos de « simulation », du coup,
en se référant aux tentatives de définition de la vie,
pourquoi ne pourrait-on pas considérer la simulation de la vie comme elle-même, de la vie/vye ?
A commencer par le jeu de la vie de Von Neumann :
– structure dissipative : oui car la simulation électronique avec un ordinateur est dissipative,
– auto-catalyse, oui avec les règles de création de la vie pour une cellule suffisamment entourée, mais pas trop,
– homéostasie : pas vraiment, mais n’est-ce pas une question de mesure ? l’homéostasie d’un léopard est limitée : si plus de nourriture, ou si tombe d’un ravin, la structure ne pourra pas se maintenir,
– apprentissage : non, mais on pourrait coder de l’apprentissage
A continuer bien sûr, par les simulations présentées dans cet article/vidéo et avec les travaux de Stuart Bartlett qui inclura certainement un mécanisme d’apprentissage.
??
d’ailleurs, selon certains penseurs (comme Nick Bostrom) ou physiciens, nous vivons peut-être déjà nous-mêmes dans une simulation !!!
euh, je voulais dire le jeu de la vie de Conway, pas Von Neumann
Peut être un peu hors sujet comme question, mais comment fais tu pour que les conditions initiales se décident interactivement à la souris ?
Merci pour tes vidéos !
C’est codé en C# sur Unity (un moteur de jeu vidéo), et donc je récupère les coordonnées de la souris pour injecter de la concentration dans le modèle en temps réel.
Bonsoir,
Pour ceux qui voudraient poursuivre la réflexion et en remerciement pour votre superbe vidéo sur le facteur de confusion, quelques approfondissements plus solides, dépouillés d’une sémantique anthropocentrée, par François Roddier qui le théorise depuis longtemps.
Sa conférence de 2010 : https://www.youtube.com/watch?v=6lNz5vmKEFA
Et sur son site : https://www.francois-roddier.fr/
Pour prolonger, il y a les excellents cours de Jean-François Joanny au Collège de France. Ils sont filmés et le premier m’avait beaucoup intéressé et aborde des concepts proches de ta vidéo : https://www.college-de-france.fr/site/jean-francois-joanny/course-2019-02-18-15h30.htm
Merci mon cher ! Je ne connaissais pas ce cours, mais je sens qu’il faut que j’aille regarder ça !
Merci pour cette super vidéo 🙂
Je suis un poil déçu (mais juste un ^^), je pensais que tu allais répondre à la question que je me posais à la fin de la vidéo précédente. Je maitrise pas bien le concept d’entropie mais j’espère que ma question sera clair.
Où va l’entropie des espèces vivantes ? Si on prend genre l’ensemble des espèces vivantes (végétaux, microbe ..) sans/avant les animaux, c’est quoi leurs « déchets ultimes », celui qui n’est exploitable par aucun être vivant ? Juste de la dissipation thermique ?
Je sais pas comment axer ma recherche d’article pour trouver réponse à ma question comme j’appréhende pas très bien le concept d’entropie.
(C’est mon premier commentaire depuis ton article « Les automates cellulaires élémentaires », alors j’en profite pour te dire que tu vulgarises super bien et que c’est génial d’avoir ton blog pour se donner envie d’aller voir les sources ^^’)
Merci pour le commentaire 🙂
Oui le déchet ultime c’est de la dissipation thermique. Tu peux par exemple voir une plante comme un système qui absorbe des photons UV (de haute énergie) et ultimement rejette des photons dans l’IR lointain, et ça c’est de la dissipation d’énergie libre.
Bonjour,
Super vidéo (je l’ai regardée 2 fois) et billet. Le source code des simulations est-il disponible?
Je serai très intéressé d’y jeter un œil 🙂
Salut David,
Tout d’abord encore bravo pour la qualité de ta vidéo et de tes explications. Ça fait bon nombre d’années que je te suis et la qualité ne défaille pas!
J’essaie de comprendre avec les mains si on aurait pu anticiper la création des cellules. Et je pense qu’il me manque un ingrédient. Prenons une cellule entourée de plusieurs autres de sorte qu’elle soit stable. En un point de cette cellule je comprends cette stabilité comme un subtil équilibre entre le taux d’apparition de B et son taux de disparition par diffusion et destruction. Comme B est plus concentré au centre, au bilan il a plutôt tendance à y être créé en grande quantité et diffuser vers l’extérieur. Ceci donne l’impression que la cellule puise exclusivement dans son sein les ressources pour s’entretenir. Or dans ta vidéo, les cellules sans voisine se divisent et se propagent, même en partant d’un état stable comme tu le montres lorsque tu supprimes des cellules à la souris. Qu’est ce qui fait qu’un point à la frontière entre deux cellules stables, ayant une concentration quasi nulle en B, bloque la division cellulaire, alors que le même point avec la même concentration en B permet la division s’il n’y a pas de voisine? Mon intuition me dit que la concentration en produit A y est différente (plus faible dans le cas stable que dans le cas de division cellulaire), mais visiblement tu expliques que la simulation utilise une concentration constante et uniforme de A. Qu’est ce que j’ai raté?
Merci à toi encore une fois, super boulot!
Non tu as parfaitement raison, en fait j’ai dit que la concentration est stable et uniforme, mais ça n’est pas tout à fait vrai. Il y a un facteur de réapprovisionnement de A, et donc une cellule, en plus d’être un pic de concentration en B, est un « trou » de concentration en A.
Bonjour,
Merci pour ta série de vidéos, le sujet est vraiment très intéressant.
Dans ta modélisation, une chose m’échappe.
– Si A est plus ou moins constant car « réapprovisionné
– Si A + 2B => 3B
Pourquoi arrive-t-on à des zones sans B (noires dans la vidéo) à la fin de la modélisation ?
Ne devrait-on pas avoir la présence de B partout car le substrat A ne s’épuise pas et le substrat B est aussi le produit donc croissant ?
Je peux clarifier si ce n’est pas assez compréhensible, merci pour ta réponse et tes vidéos !
Oui mais B subit aussi une dégradation progressive (il a l’équivalent d’une demi-vie)
Très bien, merci pour la réponse
Merci pour cette vidéo à mi-chemin entre de la vulgarisation et de la recherche compte tenu de tes simulations extraordinaires. Le fait qu’il soit finalement plus simple de recourir à des simulations qu’à des expériences de chimie comme tu le fais remarquer laisse clairement envisager que l’on parvienne à simuler numériquement une authentique forme de « lyfe » bien avant de pouvoir éventuellement la synthétiser chimiquement. On peut même s’attendre à ce qu’une telle simulation soit obtenue à court ou moyen terme (y compris peut être par ta contribution). Il est intéressant de se demander quelle serait la perception ou la réception d’un tel résultat dans la communauté scientifique et auprès du public. J’imagine que pour beaucoup, et même dans la communauté scientifique, le fait qu’il ne s’agisse « que » d’une simulation informatique serait un critère déterminant pour considérer qu’il ne s’agit pas de quelque chose de vivant ou même de vyvant. En tout cas je suis impatient de voir ce que donneront les recherches en ce sens.
Merci pour ce billet qui m’a bien aidé à récapituler tout ça. C’est la toute première vidéo ou j’ai eu du mal à suivre. Peut être que le sujet m’intéressait moins inconsciemment.
En tout cas, comme d’hab’, merci pour tout.
Un sujet intéressant en effet !!!
Je connaissais déjà un peu les travaux d’England (« statistical physics of self replication ») mais je n’avais jamais entendu parler de Barlett. Je vais (essayer) de lire tout cela si je trouve le temps.
Petite question concernant le diagramme de Venn présenté dans l’article :
Ou situerais-tu les ordinateurs dans le diagramme ? Intuitivement je dirai en (7) car ce sont des structures dissipatives, ils possèdent une sorte d’homéostasie et ils sont capables d’apprendre.
Mais ils sont peut-être en (9) car on pourrait tout à fait envisager d’en construire avec une capacité d’auto-catalyse non ? .
Dans ce cas la les ordinateurs seraient vyvant !!!
En tout cas merci encore pour ton travail
Si je me souviens bien dans la publication, Bartlett classe par exemple en 7 une maison connectée avec un système de domestique.
Pour l’auto-catalyse, il faut des ordinateurs qui puissent construire d’autres ordinateurs (hors d’un environnement humain, donc capacité à fabriquer du silicium, des processeurs, etc.)
Merci David pour ces superbes épisodes comme d’habitude. Est ce qu’il y en aura un troisième qui abordera la définition de la vie sous l’angle de l’information ?
C’est une approche qui commence a être développée par exemple dans le livre de Pierre-Henri Gouyon dans son livre « Le Fil de la vie, La face immatérielle du vivant ».
C’est malheureusement un sujet difficile car l’information n’est pas encore un concept très bien défini comme l’écrivait Tom Stonier qui appelait de ses vœux une nouvelle physique intégrant plus largement le concept d’information dans son ouvrage « Information and the Internal Structure of the Universe ». Mais heureusement les sujets difficiles n’ont pas l’air de vous effrayer ☺ !
A propos de l’entropie , on peut faire remarquer qu’elle peut être également associée à de l’énergie mécanique, et non exclusivement à de la chaleur.
prenons le cas d’un ressort, on peut considérer que le fait de tirer sur sa longueur va provoquer un arrangement particulier des atomes éloigné de sa position d’équilibre correspondant
à une entropie plus faible dans la mesure où ce nouvel état est moins probable que si il était naturellement au repos. En retour, l’augmentation de son entropie vers un état plus probable va provoquer la force de traction. Ce modèle a été utilisé par E. Verlinde pour reformuler les lois de Newton et la Gravitation à partir de l’entropie et de la théorie de l’information. https://arxiv.org/abs/1001.0785
Bonjour,
Vidéo très intéressante. L’utilisation de la souris pour modifier les conditions initiales et très intrigante aussi
et possède une forte valeur pédagogique et ludique pour divers phénomènes simulable en 2D.
J’aurais néanmoins deux questions, une quasi philosophique (que je pose pour la réflexion) et l’autre plus technique.
Admettons que l’on trouve N réactions chimiques dont on pourrait prêter un comportement d’apprentissage
serions nous satisfait de définir le procédé comme vivant alors que ce ne sont que des réactions chimiques ?
Au final nous le somme aussi, mais pouvons nous quantifier à partir de quel complexité N un système peut être considéré comme vivant ou non ? Donc cette étude ne se résumerait elle pas à définir la plus petite complexité Nmin qui défini un être vivant ?
Et question technique :
A quoi est due la taille caractéristique des structures de la simulation ? De la taille de la perturbation (gaussienne j’imagine) ? ou peut être de la vitesse de diffusion ? Il serait alors curieux de faire varier ces grandeurs au cours du temps ou de l’espace voir si d’autres structures apparaissent et quel serait le comportement d’une telle simulation.
La question philosophique : je pense que ça aurait pour effet de nous interroger s’il manque quelque chose dans la définition, et ce qui nous ferait (fondamentalement) penser que même un ensemble de réactions satisfaisant les 4 critères n’est pas vivant.
La question technique : oui c’est une compétition entre la diffusion et les paramètres de dégradation du produit B.
Merci David pour la vidéo, c’est un sujet assez ardu que tu arrives à simplifier à merveille.
Voici un lien qui manque d’explications mais qui permet de faire tourner sur le navigateur le diagramme de phase de Gray-Scott. Avec en bonus le fait que si vous cliquez sur un point du diagramme de phase, alors se lance la simulation associée.
https://www.shadertoy.com/view/MljcW1
Petit commentaire sur les cellules de convection : tu aurais pas pu avoir des cellules hexagonales dans ta soupe, c’est trop turbulent. La photo que tu montres avec de beaux hexagones, c’est pas tout à fait du Rayleigh-Bénard en fait, c’est du Bénard-Marangoni : la tension de surface joue un gros rôle.
Merci pour le lien, ça n’a pas l’air de tourner chez moi mais ça doit être dû à ma machine ou mon navigateur.
Et sinon oui bien vu pour Bénard-Marangoni !
Bonjour, super vidéo !
Je me posais une petite question technique, comment as tu implémenté les réactions diffusions ? Avec un Automate Cellulaire, avec chaque cellules contenant les données de chaleur et de concentration des espèces ? Je m’intéresse beaucoup à la programmation et aux algorithmes et je suis assez curieux de connaître ton approche. Si tu as suivi un article / papier de recherche, serait il possible d’avoir une référence ou un lien ?
J’aime beaucoup ton contenu et les sujets que tu abordes ! Merci de rendre ça accessible à tous gratuitement !
Non ça n’est pas un automate cellulaire (pour laquelle l’ensemble des états de chaque cellule est fini, genre 0/1) mais une « simple » simulation des équations différentielles associées.
Bonjour,
Merci pour cette video, c’est tout simplement fantastique.
Je fait de la recherche sur la diffusion des molécules d’eau dans le coeur en IRM. Je fait des simulations du même type dans ma recherche mais plutôt de type « particule base » (je simule les chocs entre molécules d’eau). En lisant les commentaires plus haut il semble qu’ici tu simules directement les équations différentielles. J’adorerais reproduire tes simulations (je pense que c’est plus efficace que de simuler le mouvement des molécules une par une :D) mais je sais pas trop où commencer . Par hasard aurais-tu un lien ou un exemple de code pour apprendre à simuler ce type d’équa diff ?
En tout cas merci pour tes vidéos, c’est juste un régal.
Kévin
Je trouve que le concept d’apprentissage est assez mal défini. Par exemple, dans ta démo avec les cellules de convections, on peut dire que l’organisme a ‘appris’ des infos sur son environnement, en effet, en observant le système (la position et la rotation des cellules), on peut en déduire des propriétés des cellules de convection (l’environnement). Il y a donc un ‘transfert’ d’information entre l’environnement et l’organisme et donc une forme ‘d’apprentissage’. L’auteur du papier Lyfe semble lui même avoir des difficultés à proposer une définition précise:
Learning—The ability of a system to record information about its external and internal
environment, process that information, and carry out actions that feed back positively on its
probability of surviving/proliferating. […] Hence, “learning” is an umbrella term for this large and incompletely understood set of processes.
Qu’est ce qu’il entend concrètement par ‘enregistrer et processer l’information’? Aussi son critère d’homéostase peut-être vu comme une forme particulière d’apprentissage et apparaît redondant.
Autre point curieux, il semble se contredire: il donne des exemples de systèmes avec dissipation, autocatalyse et apprentissage (mais sans homéostase) en désignant les organismes vivants (sic) qui s’autodétruisent. Doit-on en déduire que si l’Homme ne parvient pas à survivre au réchauffement climatique, il ne devrait pas être considéré comme vivant, car incapable d’homéostase? Que dire des organismes qui ont disparus lors de la grande oxydation, n’étaient-il donc pas des êtres vivants au sens de Lyfe?
EXCELLENT. Je ne connaissais pas ce domaine de recherche.
J’en ai beaucoup appris : merci à David et aux commentaires de chacun.
Ce blog donne un éclairage complémentaire. BRAVO
Merci beaucoup pour cette présentation passionnante qui montre en particulier comment des petits modèles simples peuvent aider à comprendre l’émergence de systèmes aussi complexes que les systèmes biologiques.
Sinon, sur le paradoxe de l’incompatibilité apparente du second principe avec le vivant, on peut précisément le comprendre en restant sur des considérations purement entropiques. Dans l’interprétation de Boltzmann, l’entropie représente la probabilité d’un état macroscopique (puisqu’elle est directement le logarithme de son nombre de micro-états). L’entropie augmente pour un système isolé parce qu’on ne peut accéder qu’à des états de plus en plus probables : a priori il n’est pas impossible de revenir en arrière, mais c’est peu probable et pour des états de taille macroscopique (limite thermodynamique) cette improbabilité est tellement faible qu’elle devient en pratique une impossibilité. Si un système vivant est un système qui maintient son entropie basse et peut même la diminuer, on voit que l’incompatibilité apparente de la vie avec le second principe signifie simplement que l’on ne comprend pas comment des organisations vivantes hautement improbables peuvent être formées à partir d’un état initial très désordonné. Le second principe n’a donc ici rien de mystérieux : il s’agit simplement de comprendre comment des structures aussi bien définies qu’un être vivant peuvent spontanément se former alors qu’au départ on a une matière totalement dispersée. Il n’est même pas nécessaire de connaitre le second principe pour s’interroger sur ce fait étonnant !
La réponse thermodynamique (à la Prigogine) nous dit que c’est parce que le système est ouvert. C’est possible parce que le vivant relargue dans le même temps de l’entropie au milieu extérieur. Autrement dit l’extérieur va dans le même temps accéder à des états macroscopiques de plus en plus désorganisés, ce qui au niveau de l’univers rend la transformation possible. La vie se maintient parce qu’elle relâche de l’entropie ce qui rend les transformations probables.
On peut aller plus loin en se demandant comment en pratique cette entropie est transmise. Dans l’exemple de l’arbre sur la video, c’est assez clair : il absorbe quelques photons de haute énergie (dans le visible) avec une basse entropie tout en émettant de nombreux photos de basse énergie (dans l’IR) avec une haute entropie. La vie existe car elle absorbe de l’énergie faiblement entropique (photosynthèse ou alimentation) en relâchant une quantité équivalente d’énergie hautement entropique (rayonnement ou chaleur – je me demande d’ailleurs si ce n’est pas pour cette raison que le corps humain est confortable à 25 oC et pas à 37 oC – pour relâcher l’entropie). Tout cela rend in fine les structures de la vie probables.
Maintenant, on peut quand même constater que cela ne résout pas tout à fait le problème car il reste le paradoxe de Boltzmann : si la vie rejète l’entropie pour se maintenir et se développer, au niveau supérieur (système solaire ou univers) cela veut dire que l’entropie globale augmente. Il a donc été dans le passé avec une entropie très basse. On relie de nos jours cela avec le Big-Bang, mais à l’époque de Boltzmann où l’univers paraissait immuable c’était très étonnant. On pouvait penser qu’existant de toute éternité l’univers avait eu le temps de faire des fluctuations complètement improbables et donc il avait pu arriver par hazard à un état de basse entropie qui ensuite avait permis le développement de la vie. D’après le théorème de Poincaré, ces fluctuations complètement improbables sont mêmes certaines dans l’éternité à condition que l’univers soit fini. Dit de cette façon l’existence de la vie nous fait arriver à l’idée que l’univers est fini : c’est une conclusion assez imprévue, mais thermodynamiquement le raisonnement n’est pas complètement absurde !
Bon cela nous mène un peu loin, mais encore bravo et merci pour vos videos !
Merci pour le commentaire !
Tiens je n’avais jamais entendu cet argument pour la finitude de l’Univers à partir du théorème de récurrence de Poincaré !
Bonsoir
Je viens de regarder votre dernière vidéo, je crois qu’il me sera nécessaire de la regarder plusieurs fois. Mais je suis impressionné par la clarté de vos explications, qui même si on ne comprends pas tout me laisse une impression de mieux connaître le sujet.
Merci pour la qualité de vos explications, je ne regrette qu’une chose c’est de ne pas avoir eu ces vidéos il y a 40 ans……j’ai 74 ans
Bonjour
Super vidéo comme d’habitude. Je suis fan.
Petite question : on dit que le léopard (et les autres êtres vivants) est « organisé ». Certes, cela parait intuitif.
Mais comment définit-on l’organisation ?
Merci
Christophe
Une façon de le voir, c’est l’hétérogénéité spatiale (à plein d’échelles). Si on prend 1mm3 de léopard à deux endroits différents, ils sont différents (marche aussi avec 1cm3, 10cm3). Si le léopard était « de la soupe », ce serait homogène
Re,
donc, si je comprends bien, on définit « organisation » comme une homogénéité, sans davantage définir homogénéité.
Je suis surpris que l’ensemble du concept d’entropie, que je ne maitrise pas certes, ne soit pas plus définie que cela.
Encore merci pour vos vidéos très instructives
Bonjour, désolé de poster un commentaire qui n’as rien à voir avec cet article mais, je viens de revoir ta passionnante vidéo sur la « machine à inventer des mots » et j’ai tenté via l’article d’accéder à un message d’erreur, je me demandais si tu pouvais le reposter ou me l’envoyer par mail si tu l’as encore à cette adresse h.lefevre966@laposte.net. Merci d’avance et félicitation pour ton contenue.
Il y a cet article là qui est une version mise à jour : https://scienceetonnante.com/2015/11/06/la-machine-a-inventer-des-mots-version-ikea/
Quand je vois écrit « Entropie » depuis que j’ai vu Tenet, j’ai la paupière qui saute :'(
Pingback: My Take on LYFE Part I: Expectations and Hype – A Journey To Another AI
Bonjour et merci pour vos superbes vidéos.
Il y a quelque temps, j’ai eu le plaisir de présenter une conférence tout publique ou j’aborde en 2e partie un modèle assez général pour décrire le concept d’entropie avec son aspect informationnel et son homéostasie. Cette dernière n’apparaît pas en tant que tel mais via une boucle informationnelle entre le système étudier et son environnement (système auto-régulé). Si cela intéresse voici un lien ou je décris le modèle: https://forums.futura-sciences.com/discussions-scientifiques/769453-aborder-lenergie-lentropie-structures-lenseignement-secondaire.html
Je peux aussi donner les liens vers la conférence et le support sur lequel je m’appuie
Bonjour,
Je ne suis pas scientifique mais je regarde nombre de vos vidéos sur you tube et j’ai presque l’impression de comprendre, c’est un exploit de votre part. En tout cas merci pour la passion que vous ne manquez pas d’exprimer.
J’écris mon premier bouquin d’anticipation dont le thème principal est l’entropie, celle-ci étant le principe premier (pardon pour le pléonasme) de la « diffusion » de la vie et de toute la matière de l’univers, énergie et information comprise bien sûr. Je cherche désespérément des informations simples en français sur la relation au temps de l’entropie autre que celles de Brian Greene dans l’Univers Elégant (je crois).
Serait-il exagéré de ma part de vous demander de faire une vidéo à ce sujet ?
Bien à vous
Vraiment super ! franchement c’est excellent je me suis régalé.. Merci pour ce travail David ! Par contre chose étrange si j’essaye de résumer ce que j’ai appris j’ai du mal à trouver quelque chose 😀 ha ha…
C’est que le sujet est sans doute fantastiquement compliqué même si en apparence ça semble accessible et j’ai peur qu’on fasse un peu d’anthropomorphisme entre les « cellules » qu’on croit voir et les petits agrégat de matière B 🙂
A mon avis on est assez loin de trouver une « simulation informatique » qui soit vraiment « vivante », au sens « cellules qui évoluent et se défendent contre la destruction » (la notion de défense, ou de résilience, est à mon avis essentielle dans la vie) même si j’ai la ferme intuition que c’est possible.
bonsoiir David, je suis avec grand intérêt tes post sur des sujets de physique; là je suis un peu déçue…. Etant biologiste, je trouve difficile de ne pas intégrer dans la définition d la vie le « pilier » : capacité reproductive et maintien des caractéristiques d’espèce dans la descendance…. merci quand même c’était intéressant de voir cette interprétation. quoi qu’il en soit, l’idée force est qu’effectivement , la plupart de s gens qui parlent de forme de vie font toujours référence à la « vie sur terre »; c’est donc fondamental de dégager des concepts « plus larges »
Bonjour,
Dans cette vidéo, je ne fais que vulgariser les travaux d’autres, ça n’est pas moi qui a décidé quel « pilier » intégrer 😉
Après la capacité reproductive est induite par l’autocatalyse.
Superbes vidéos qui sont arrivés à pile poil pour moi !
Depuis quelques temps je me questionnais sur les concepts d’entropie et des répercutions que cela engendre. On m’avais conseillé de livre le livre de François Roddier (dont certains on déjà parlé dans les commentaires) « Thermodynamique de l’évolution ».
La vidéo m’a bien facilité la lecture du livre qui s’est avéré super intéressant.
J’aurais bien aimé avoir ton avis sur le travail de M.Roddier. J’ai vraiment été séduit par sa manière de prendre du recul sur tout ce qui pourrait découler des principes thermodynamiques. Le livre ouvre sur des perspectives vraiment intéressantes.
Encore merci pour cette vidéo ainsi que pour l’ensemble du travail que tu fais. Il y a dix ans je me souviens avoir cherché des renseignements sur l’expérience d’Alain Aspect sans en trouver à ma portée ; et j’en ai trouvé récemment dans ta vidéo ! Avec Mr Aspect en personne !! Chapeau !
Merci infiniment pour votre travail, notamment pour cette vidéo et ce billet.
Je me demandais simplement: serait-il abusif de conclure de ces travaux que la société humaine est en elle-même un organisme vyvant? Il s’agit bien d’une structure dissipative, capable d’auto-catalyse, capable (pour l’instant) d’homéostasie et qui d’apprentissage (au sens large) non?
Merci 🙂
Bonjour David,
Merci beaucoup pour cette vidéo qui m’a beaucoup intéressé et intrigué! Je reste bloqué tout de même sur cette notion d’entropie (ahah dsl!). Voici quelques questions fondamentales:
– les forces fondamentales (gravité, électrostatique) ont tendances a créé des structures ordonnées (planètes, molécules) sans pourtant piocher de l’énergie de l’extérieur..
– Si l’entropie ne fait que augmenter… l’univers au temps infini sera une soupe parfaitement homogène… ça me semble.. désespérant!
– Si je place une paroi semi-perméable dans un récipient (comme par exemple les micelles d’acides gras à l’origine de la vie comme présenté par la dernière de Passe-science 😉 )… je vais avoir une sélection avec les petites molécules à droites (à l’intérieur ) et les plus grosse à gauche (extérieur), sans nécessiter de l’énergie par ailleurs!
Si quelqu’un arrive à répondre à ces questions qui me torturent, je lui en serait infiniment reconnaissant!
Merci encore et bravo!
Tanguy
Brillantissime. Merci pour cette vidéo et d’une façon générale pour cette chaine absolument passionnante
Merci pour ces videos et votre remarquable travail de vulgarisation.
Une question d’un néophyte sur l’entropie.
L’univers à son départ était dans un état d’entropie maximale et c’est un système fermé, comment a t il pu s’organiser ?
Bonjour et merci pour ton site et tes excellentes vidéos ! Sur le papier de Turing je me souviens d’une conférence grand public assez sympa https://vimeo.com/26959129 mais ce sera une bonne idée de faire une vidéo dédiée.
Robin
Pingback: Entropie | Pearltrees
Pour le quatrième pilier de Bartlett, il s’agirait peut-être de nous observer « Nous », analyste scientifique, internaute amateur, personne de tout poil s’intéressant à la science, ceci n’excluant pas non plus tout quidam être vivant, sensible et doué de conscience : non plus le « chat de Schrödinger » mais, « Schrödinger » lui-même.
Ce serait passer un cran supplémentaire (ultime ?) et prendre comme sujet d’expérience non pas « la vie dans la nature » mais la « nature dans la vie », non plus un objet ou sujet d’expérience scientifique mais un « sujet comme expérience scientifique » ou encore un « sujet comme objet scientifique », selon qu’il est vu sous l’angle d’une observation objective délimitée dans ce même cadre scientifique. On rejoindrait Freud en passant du courant de la psychologie behavioriste au courant systémique de l’école de Palo Alto, base de la cybernétique et du transhumanisme moderne, annonciateurs de l’ère numérique au point de départ de la Silicon Valley.
C’est l’expérience qui a peut-être lieu en ce moment et de longue date, localement et globalement , dans laquelle nous sommes interconnectés (vidéos, blogs, publications scientifiques…) et où nous nous observons nous-mêmes comme entités soumises, primordialement, à des contraintes morales, donc immatérielles, mais capables de choisir ou non de les affronter, pour donner sens à notre vie car nous y aspirons profondément, ou plutôt de sourire à la vie par liberté en nous sentant plus spécifiquement concernés par notre prochain (ici l’approche scientifique dépasse le psychologique et devient politique ou sociale car elle ne concerne plus « l’individu interagissant avec le monde » mais « le monde composé d’individus variés dotés de dénominateurs communs »).
Il y a bien un système ouvert et un système fermé comme peut l’être un circuit électrique ayant plutôt tendance à se relier à la terre en cas de différentiel de courant pour protéger l’usager, ou à disjoncter, se sectionner pour éviter la surchauffe. L’étude de tous les phénomènes observables, même ceux qui ne peuvent se voir.
Mais c’est de la science, ça ne dit rien de nous directement face à notre destin d’homme. Il faut peut-être creuser dans l’œuvre de Georges Canguilhem ou de Jean Baudrillard ou même Hegel et Leibniz pour élargir la recherche…
Merci pour la vidéo documentée et votre regard d’analyste !
Bonjour,
j’apprécie beaucoup votre travail et la qualité de vos vidéos. C’est très agréable à suivre.
A 17min03, dans la vidéo YouTube, vous présentez une équations de réaction-diffusion pour simuler un feu de foret. Existe-t-il un article scientifique dans lequel vous avez trouvé cette équation?
Je vous remercie de votre réponse!
Matthieu Brachet
Non j’ai juste posé ça comme des équations « naturelles » pour le phénomène, c’est évidemment très simplifié comme modèle.
Oui c’est linéaire mais ça n’en reste pas moins intéressant!
Je vous remercie pour la réponse. Bonne journée
Pingback: Thermodynamique de la vie – L'émergence de la vie sur terre
Coucou,
Un collègue me faisait une remarque assez intéressant : un virus est un cas limite de « life´´ en tout cas pas vraiment vivant au plein sens du terme, mais semble un cas de « lyfe´´ incontestable, dans quelle mesure cette assertion est elle raisonnable ?
Amicalement.