Dans la vidéo du jour, on étudie les liens profonds entre magnétisme, électrostatique et relativité restreinte. Et on démontre que la force magnétique découle naturellement de la force électrostatique (la loi de Coulomb) et de la relativité restreinte.
Comme d’habitude : quelques précisions sur des choses où je suis passé un peu vite. Parlons des aimants, de mu0, de Galilée, des frottements et de Feynman !
Qu’est-ce qu’un aimant permanent ?
J’ai rapidement évacué cette question…car elle n’est pas simple ! Ou du moins elle n’est pas simple à traiter en lien avec l’explication traditionnelle des électro-aimants (disons la loi de Biot et Savart). Cela mériterait bien une vidéo ou un billet complet ! Mais on peut noter que le phénomène trouve son origine la fois dans les orbites des électrons (qu’on peut à la limiter qualifier de courant qui circule de façon spontanée) mais aussi le spin (qu’on pourrait voir comme une charge en rotation, donc un courant, mais c’est pousser trop loin l’interprétation « rotation » du spin). J’ai en tête que la contribution des spins est d’ailleurs en général supérieure à celle des moments orbitaux, mais à voir.
Bon clairement il faudra une vidéo !
Comment mesurer mu0 ?
Contrairement à ce que j’ai laissé penser, la valeur de mu0 ne se détermine pas expérimentalement…elle est très exactement fixée ! La raison est que c’est l’expérience d’Ampère qui sert à déterminer l’unité qui porte son nom. Et donc la constante mu0 s’en trouve automatiquement fixée à une valeur donnée.
C’est analogue à ce qu’il se passe avec la définition moderne du mètre qui se base sur la distance parcourue par la lumière, et donc la vitesse de la lumière s’en trouve fixée par définition ! Mais on aurait pu faire autrement. Aujourd’hui l’unité de charge, le coulomb, n’est pas une unité fondamentale. Elle découple de la définition de l’ampère.
Imaginons qu’on ait défini une unité de charge comme fondamentale, disons « la charge d’une mole d’électron », et l’unité de courant à partir de là, alors il aurait fallu mesurer mu0 !
Erratum ! (Merci Mickaël !)
Depuis 2019, c’est bien la valeur de e qui est fixée, et donc la valeur de mu0 qui est mesurée expérimentalement ! J’avoue que je l’ignorais.
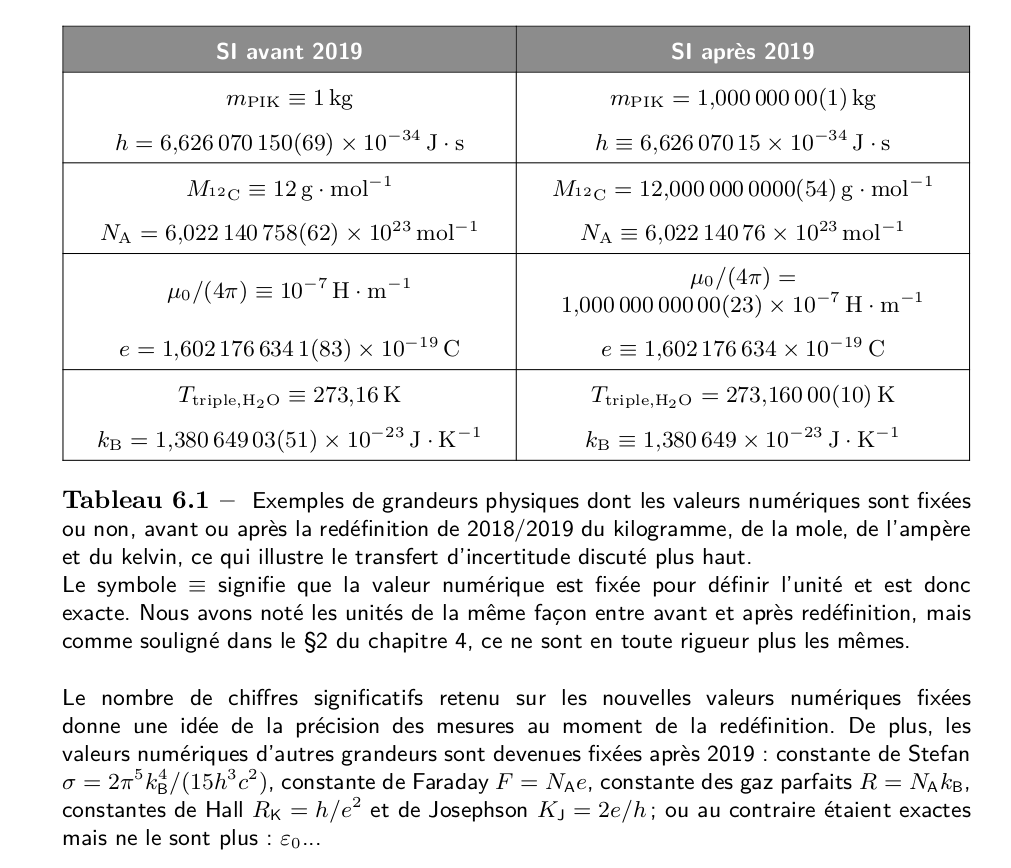
« Le mouvement est comme rien », vraiment ?
De façon amusante, je me suis amusé à chercher la source de cette citation…il n’y en a pas ! Et manifestement elle n’existe qu’en français ! J’ai tenté avec quelques traductions approximatives en anglais ou en italien, mais je n’ai rien trouvé. J’ai l’impression qu’un auteur français a du « inventer » cette citation à un moment donné. Mais qui ?
D’après Google Ngrams, l’effet a commencé dans les années 1960.
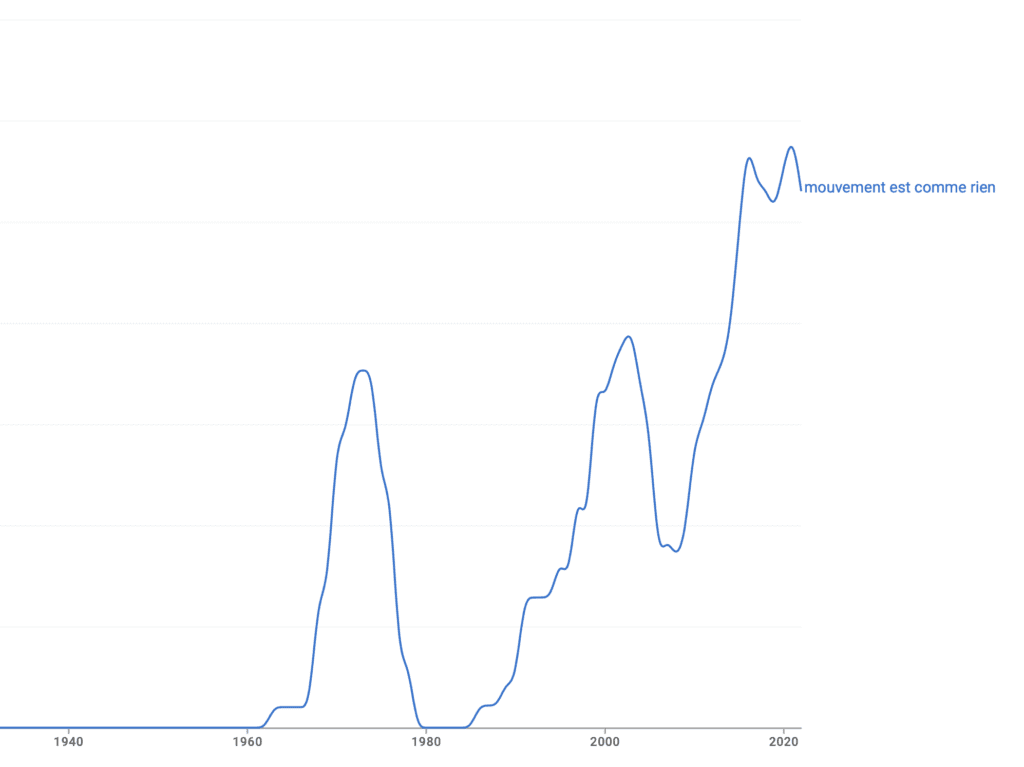
Et d’après Google Books, on trouve une occurence en 1965.
Si quelqu’un a une idée, je suis preneur ! Aidez-moi à reconstituer l’histoire de cette fausse citation !
Et les frottements alors ?
Je dis dans la vidéo qu’une force qui dépend de la vitesse, c’est suspect. Vous pourriez me rétorquer l’exemple des frottements fluides !
Sauf qu’en réalité ce qui entre en jeu dans l’expression de ces forces de frottements, ça n’est pas la vitesse, mais la différence de vitesse entre l’objet et le fluide (qui elle est invariante par changement de référentiel galiléen, du moins en relativité galiléenne), le fluide étant généralement immobile dans le référentiel d’analyse. Ouf, on ne peut pas annuler les frottements en changeant simplement de référentiel !
Que fait Feynman ?
Dans son paragraphe sur magnétostatique et électricité, Feynman reprend en gros l’analyse que j’ai présentée en premier, avec la contraction des longueurs.
Mais il en fait un traitement quantitatif seulement dans un cas particulier : celui où le courant et la particule vont exactement à la même vitesse. C’est un cas très spécial mais c’est déjà ça. Donc il emploie ce raisonnement que j’ai qualifié de « pas très rigoureux »… mais comme Feynman est Feynman, il nous montre qu’il en est parfaitement conscient ! Il valide a posteriori que ce qu’il a fait donne le bon résultat en examinant les forces et les variations d’impulsion dans les deux référentiels
22 Comments
Bonjour !
Très impressionnant comme toujours !!
Je me demande comment vous prenez le temps de faire tout ça, de si bonne qualité (forme et contenu).
Une remarque : à la fin de la vidéo, on aurait pu mentionner la formule reliant epsilon0, mu0, et c2 : le produit des 3 est égal à 1 (en tout cas c’était comme ça de mon temps …), je trouve que c’est une belle formule.
A propos de c : une idée pour une nouvelle vidéo : montrer que c n’est pas fondamentalement la vitesse de la lumière, mais que c’est la vitesse maximale « cinématique » possible due aux propriétés « géométriques » de l’espace.
Je me base sur un article de mon ancien prof de physique Jean-Marc Lévy-Leblond, montrant mathématiquement (par la théorie des groupes) que l’espace (supposé homogène et isotrope) possède une vitesse limite c, et donc que
la lumière subit cette vitesse limite comme tout le monde.
Arvin Ash a fait quelques vidéos en rapport avec cela :
Why No One Knows If Photons Really Are Massless: What if they Aren’t?
https://www.youtube.com/watch?v=c5BPZy2_7U8
How Faster than Light Speed Breaks CAUSALITY and creates Paradoxes
https://www.youtube.com/watch?v=mTf4eqdQXpA
Il me semble que le sujet de ces 2 vidéos, c’est « les photons ont-ils une masse », alors que mon propos c’est justement que c n’a pas de rapport avec les photons, mais que c est une propriété quasi mécanique de l’espace.
Bonjour,
Pourrais-je avoir la référence exacte de l’article de Jean-Marc Lévy-Leblond que vous citez ?
Merci d’avance.
Bien cordialement,
André
Dans American Journal of Physics
https://www.researchgate.net/profile/Jean-Marc-Levy-Leblond/publication/252687984_One_more_derivation_of_the_Lorentz_transformation/links/00b4953b6c595305b6000000/One-more-derivation-of-the-Lorentz-transformation.pdf
J’en ai une version française si vous voulez (Laboratoire de Physique Théorique et Hautes Energies, Université Paris VII)
Ah super ça fait un moment que je voulais faire un billet sur cette construction.
Mais j’ignorais que Lévy-Leblond en était l’auteur originel ! Je m’étais imaginé que c’était un résultat classique et ancestral 🙂
Merci beaucoup pour le fichier. Je suis aussi preneur pour la version française. Même si je lis couramment l’anglais scientifique, c’est un tel plaisir de lire l’excellent Jean-Marc Lévy-Leblond dans notre belle langue maternelle !
vraiment très rassurant de savoir que tu reconnais toi-même des erreurs, cela m’incite à te suivre encore plus attentivement qu’avant. Merci pour tous ces sujets que tu traites si bien pour nous.
Bonjour merci pour cette vidéo.
Il me semblait pourtant en regardant une vidéo dont je ne me souviens plus que l’on avait démontré que le magnétisme est bien formé de particules qui pouvait entrer en collision ( et donc bloquer leur circulation) et par conséquent former un champ anarchique qui n’a pas les valeurs attendues par les équations ??
Bravo de me permettre de comprendre le magnétisme, qui me semblait encore un peu « magique ».
Si vous pouviez continuer en expliquant le fonctionnement des aimants permanents, ce serait le top.
Merci encore
Mais oui, après cette superbe vidéo, on se demande forcément: qu’en est-il des aimants permanents ? quelle vitesse/changement de repère s’il n’y a pas de courant électrique ?
(je vous écris de sous le tapis 😉 )
Merci David, encore une vidéo intéressante !
2 choses que je ne comprends pas :
1/ si j’ai bien suivi : la force magnétique est fondamentalement une force électrostatique, assortie d’un facteur lié aux formules relativistes de changement de référentiel (du fait du mouvement d’une particule chargée et des charges du fil). Mais pour un aimant permanent, vous évoquez les spins. Or, cela est une autre propriété physique que la charge électrique. Comment se fait-il qu’un même phénomène physique puisse trouver son origine dans des propriétés physiques différentes? Y a-t-il un rapport entre spin et charge? la charge n’est-elle pas une propriété fondamentale? Ou bien ces phénomènes tout deux dit magnétiques sont-ils en fait de nature différente?
2/ le champ magnétique B est-il donc aussi une illusion? également pour un aiment permanent? enfin le champ électrique E existe-t-il vraiment? je m’interroge plus largement : finalement les lois de la physique renseignent-elles sur la nature des choses? que signifie « le champ magnétique existe-t-il? » ? par exemple dire « le magnétisme est une illusion » signifie en fait, si je vous suis bien : « la force magnétique est une modélisation confirmée par l’expérience mais qui n’est pas en fait une interaction fondamentale », comme la force de gravité depuis Einstein. Mais est-ce que la force électrostatique existe plus que la force magnétique? car ce n’est qu’une modélisation finalement, plus fondamentale dans une perspective réductionniste mais rien ne dit que cela renseigne sur la nature véritable des choses. Ainsi la déformation de l’espace-temps par des masses est-elle fondamentale? Des théories évoquent la gravité comme phénomène émergent. Alain Connes parle du temps comme un phénomène émergent à partir de la variabilité quantique et de la non-commutativité. A-t-on jamais « mesuré » un champ électrostatique? ou simplement mesurer le déplacement d’une charge en présence d’un déséquilibre entre d’autres charges?
Est-ce que quelqu’un peut m’éclairer sur ces sujets? Merci !
PS : ma formation d’ingénieur m’a orienté vers la technologie plus que la physique, donc je n’ai pas de connaissance suffisante pour bien comprendre en profondeur, même si ça m’intéresse beaucoup. C’est pourquoi vos vidéos de vulgarisation m’intéressent.
Entre temps, j’ai trouvé des article sur votre site qui traitent justement de ces questions !
Je mets les liens ici pour ceux qui ne les connaitraient pas :
https://scienceetonnante.substack.com/p/le-champ-gravitationnel-existe-t
https://scienceetonnante.substack.com/p/le-champ-electromagnetique-existe
https://scienceetonnante.com/2011/06/06/la-gravite-une-force-emergente-dorigine-entropique/
Ca ne répond pas à tout mais ça donne des éléments.
Concernant le magnétisme des matériaux magnétiques, je me pose toujours la question.
Bonjour, super vidéo comme d’habitude ! 🙂
J’ai une petite question qui me turlupine.
Si on considère une particule chargée avec une faible vitesse (par rapport au labo et à la ligne conductrice, et devant c), on pourrait se dire que l’approximation classique est valable. Et donc que la force magnétique (qui existe) n’est pas due à des effets relativistes. J’imagine qu’il y a donc un problème dans mon raisonnement (je n’ai pas fait le calcul, et j’ai bien vu que c’est le produit u x v qui apparaît), mais lequel ?
Bonjour David,
Merci pour cette très belle vidéo (comme d’habitude !). C’est toujours très instructif et très inspirant même quand on est un « professionnel de la science ».
Cette présentation du magnétisme comme effet relativiste est fondamentale et devrait être mise bien plus en avant dans l’enseignement de l’électromagnétisme, ce que j’essaie de faire dans mes cours de Master sous l’œil un peu indifférent des étudiants…
J’aimerais vous signaler une petite erreur qui s’est glissée dans votre présentation : à 26:25, la loi d’addition des vitesses est erronée, il ne doit pas y avoir de racine carrée au dénominateur (on a tellement l’habitude d’en avoir en RR, ça sort tout seul…). Si on prend une des deux vitesses égale à c, on doit retrouver c, ce qui n’est pas la cas avec la racine carrée, mais bien sans. C’est la formule 5.2 de livre de French, « Special Relativity » que vous donnez en référence (très intéressante pas ailleurs pour ces beaux petits calculs pédagogiques !).
Encore bravo et merci pour votre chaîne.
Bien cordialement,
André
Dans le troisième livre de la série The Theoretical Minimum de Leonard Susskind intitulé Special Relativity and Classical Field Theory, Susskind revient au papier de 1905 d’Einstein On the Electrodynamics of Moving Bodies. Einstein fait une expérience de pensée où une particule chargée en mouvement contenue dans un fil est placée dans un champ magnétique. Dans le référentiel du laboratoire, le champ magnétique produit la force sur la charge en mouvement F= e(v x B). Dans le référentiel de la charge en mouvement, il n’y a pas de force magnétique mais une force électrique F= eE.. Voir 8.1 page 270.
Bonjour,
Vous rendez toujours la physique intéressante.
Petit complément sur le mirage de la force magnétique.
SITUATION
Sans relativité.
On a 2 charges de même signe (par exemple électrons) immobiles entre elles (au départ) et aussi immobiles par rapport à un système de référence.
La force répulsive entre-elles est la seule force électrostatique qE. Cette force entrainera une accélération qu’on mesure.
Maintenant on a les mêmes charges (immobiles entre elles) mais vues dans un système de référence en mouvement. La force électrostatique est toujours là, mais il y aura une deuxième force due au champ magnétique causé par une charge en mouvement. La charge 1 crée un champ magnétique qui entrainera une force attractive sur la charge 2 (et réciproquement). La force électrostatique répulsive est ainsi réduite par une fore attractive magnétique.
Quantitativement ça marche, mais c’est totalement incohérent de donner des explications de nature différentes en passant d’un système de référence à l’autre!
Avec la relativité.
On a 2 charges de même signe immobiles entre elles et aussi immobiles par rapport à un système de référence.
La force répulsive entre-elles est la seule force électrostatique qE.
Maintenant on a les mêmes charges mais vues dans un système de référence en mouvement. La force électrostatique est toujours là. Mais le ralentissement du temps nous donnera une accélération d’éloignement plus faible. Plus besoin du mirage magnétique.
La relativité simplifie notre description et la rend plus cohérente. On a plus d’explications de natures différentes en passant d’un système de référence à l’autre!
Merci David pour cette super vidéo !
J’ai toujours regardé l’électromagnétisme comme une poule face à un couteau et c’est assez frustrant, surtout qu’on je lis des IRM quasi tous les jours.
Je me demandais d’ailleurs si tu connaissais un moyen efficace (une référence, un cours, etc.) de comprendre le fonctionnement d’une IRM ? Parce qu’en médecine ont apprend à lire les images mais jamais comment elles sont acquises (on nous donne quelques grands principes mais c’est jamais suffisant pour avoir la sensation de vraiment comprendre ce qu’il se passe).
Merci encore !
Thomas
Bonjour,
Dans le document « Petit complément sur le mirage de la force magnétique. » il manque un détail important (en gras). Un dessin aurait enlevé la confusion!
Voir : Cours de Relativité Restreinte (F Henry-Couannier) (9. La force électromagnétique entre deux charges en mouvement) page 41
« La force totale entre les deux charges est donc atténuée par un facteur gamma par rapport à celle calculée dans le référentiel R’ de repos des charges. »
SITUATION
Sans relativité.
On a 2 charges de même signe (par exemple électrons) immobiles entre elles (au départ) et aussi immobiles par rapport à un système de référence. Elles ont la même coordonnée en x mais séparées de delta y.
La force répulsive entre-elles est la seule force électrostatique qE. Cette force entrainera une accélération en y qu’on mesure.
Maintenant on a les mêmes charges (immobiles entre elles) mais vues dans un système de référence en mouvement (sur l’axe x). La force électrostatique est toujours là, mais il y aura une deuxième force due au champ magnétique causé par une charge en mouvement (en x). La charge 1 crée un champ magnétique qui entrainera une force attractive (dans la direction y) sur la charge 2 (et réciproquement). La force électrostatique répulsive (en y) est ainsi réduite par une fore attractive magnétique.
Quantitativement ça marche, mais c’est totalement incohérent de donner des explications de nature différentes en passant d’un système de référence à l’autre!
Avec la relativité.
On a 2 charges de même signe immobiles entre elles et aussi immobiles par rapport à un système de référence. (Mêmes conditions qu’avant)
La force répulsive entre-elles est la seule force électrostatique qE.
Maintenant on a les mêmes charges mais vues dans un système de référence en mouvement (sur l’axe x). La force électrostatique est toujours là. Mais le ralentissement du temps nous donnera une accélération d’éloignement plus faible vue dans un système de référence au repos. Plus besoin du mirage magnétique.
La relativité simplifie notre description et la rend plus cohérente. On a plus d’explications de natures différentes en passant d’un système de référence à l’autre!
Bonne journée
Merci pour la vidéo. C’est la première vois que je vois une explication aussi claire et précise pour comprendre pourquoi électricité et magnétisme sont la manifestation d’un même phénomène.
Sinon je me suis intéressé à la citation de Galilée que l’on ne retrouve en effet qu’en Français et qui semble ainsi a priori apocryphe. En fait, après des recherches un peu approfondies, il apparait qu’elle ne l’est pas.
On la trouve dans son ouvrage le plus célèbre, le « Dialogue sur les deux grands systèmes du monde », dans la deuxième journée (le dialogue est divisé en journées). La source est disponible en VO sur wikisource
https://it.wikisource.org/wiki/Dialogo_sopra_i_due_massimi_sistemi_del_mondo_tolemaico_e_copernicano/Giornata_seconda
La citation se trouve page 141-142.
En italien, le passage donne
« Però notate: il moto in tanto è moto, e come moto opera, in quanto ha relazione a cose che di esso mancano; ma tra le cose che tutte ne participano egualmente, niente opera ed è come s’e’ non fusse »
La traduction est assez délicate surtout quand on ne connait que l’italien musical comme moi, mais en s’aidant de différents traducteurs automatiques et de citations du texte dans d’autres langues on arrive à quelque chose comme :
« Ainsi notez : le mouvement est mouvement et il agit comme mouvement dans la mesure où il se rapporte avec les choses qui en sont privées. Mais en ce qui concerne les choses qui se meuvent également avec lui, il est sans effet ; il est comme s’il n’était pas »
C’est ce dernier bout de phrase (« il moto […] è come s’e’ non fusse ») que l’on traduit par « Le mouvement est comme rien ».
La citation et la façon dont elle est citée correspond bien au sens de Galilée. En lisant le dialogue de façon plus large et approfondie, on comprend que le texte signifie en effet, en termes un peu plus modernes, que le mouvement d’un référentiel en translation rectiligne uniforme par rapport à la terre fait que pour les objets qui se rapportent à lui, tout se passe comme si on était sur terre, le mouvement du référentiel ne jouant donc aucun rôle. En termes encore plus modernes, on dirait qu’un référentiel en translation uniforme peut être considéré, comme le référentiel terrestre… galiléen !
J’ai proposé un traitement un peu plus « américanisé » de la question dans cette vidéo :
https://youtu.be/YQYytiD4MO0
Il s’appuie sur ces très chouettes petites notes de Daniel Schroeder :
https://physics.weber.edu/schroeder/mrr/mrrnotes.pdf
En espérant que cela puisse intéresser quelqu’un ici.
Hello.
Merci pour cette belle vidéo.
Je trouve vertigineux l’idée que la relation entre les forces électriques et magnétiques prennent leur racine dans la relativité restreinte.
Les lois de l’électromagnétisme avec les équations de Maxwell ne sont elle pas en outre à l’origine du caractère ondulatoire de la lumière et donc de la physique quantique?
On cherche souvent un lien entre ces deux théories. Cette démonstration n’en n’est elle pas un?