Dans la vidéo du jour, on parle de la mise en évidence de l’expansion accélérée de l’Univers…et dans la prochaine on verra les théories qu’on peut mettre dessus !
Un mot sur le « diagramme de Hubble étendu » que j’ai présenté dans la vidéo. Je l’ai obtenu (pour les différents scénarios) à partir d’une petite simulation (faudra que je partage le code quand il sera un peu propre). Et il y a plusieurs points que je peux préciser à ce sujet.
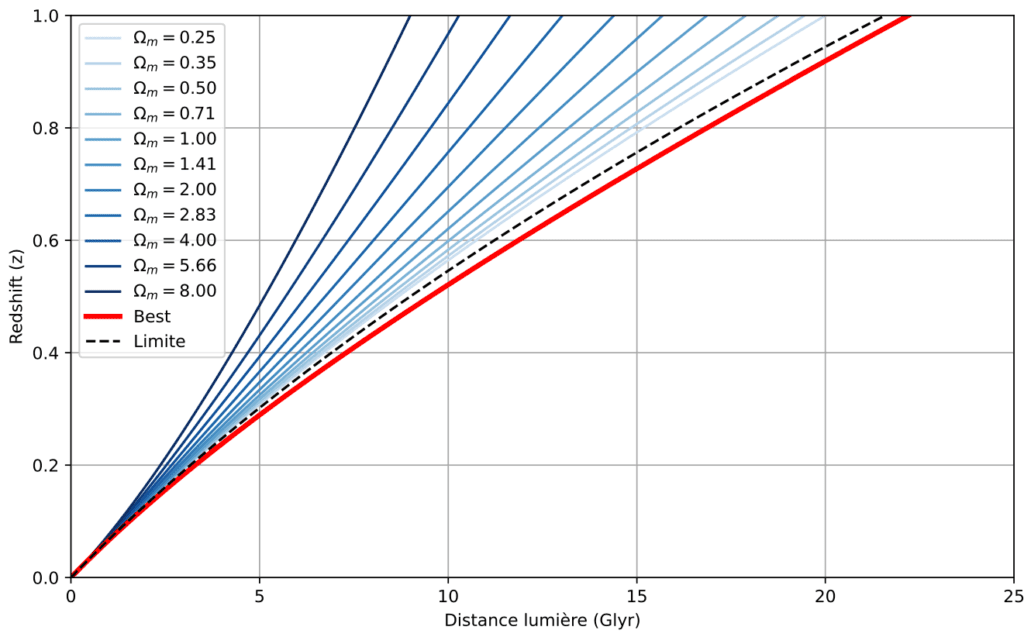
Tout d’abord les publications sur l’expansion accélérée ont tendance à publier le diagramme « distance vs redshift » avec les axes inversés par rapport à ce que j’ai fait, donc avec z en abscisses et la distance en ordonnées.
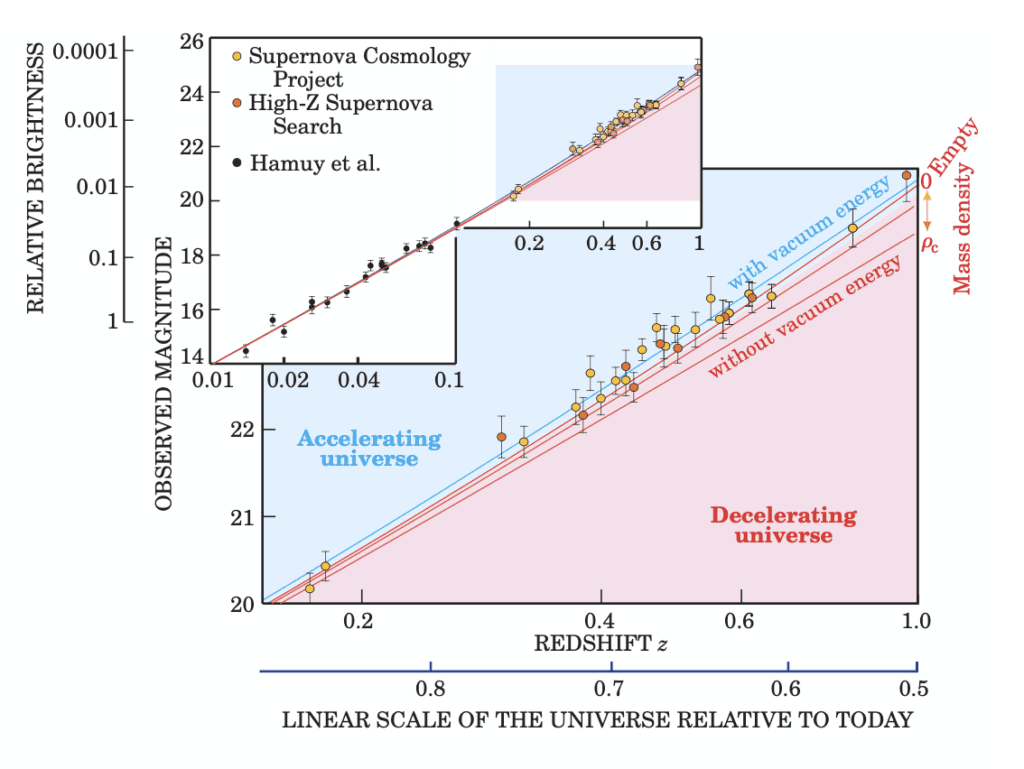
Ici par exemple le graphique dans l’article de Physics Today de Saul Perlmutter, de la collaboration High Z
Perlmutter, S. (2003). Supernovae, dark energy, and the accelerating universe. Physics today, 56(4), 53-60.
Malgré tout, j’ai choisi de faire l’inverse (distance en abscisses et z en ordonnées) pour que ça soit raccord avec un diagramme de Hubble traditionnel.
A propos de la distance
Ensuite il faut parler de « distance ». En relativité générale, la notion de distance est un peu ambigüe. On peut parler de distance propre, de distance comobile, … ici on parle généralement de distance de luminosité. La distance de luminosité d’un objet est celle qu’on déduit en comparant sa luminosité apparente et sa luminosité intrinsèque (ou sa magnitude comme sur le graphe de Perlmutter). La distance de luminosité est plus grande que la distance propre puisqu’elle prend en compte la dilatation de l’espace et donc l’allongement du trajet de la lumière. On pourrait prendre une autre distance pour faire le diagramme, mais c’est moins raccord avec les mesures expérimentales.
A propos de la vitesse
Sur la question de l’interprétation de l’expansion comme une « vitesse » des galaxies, j’ai évacué rapidement le sujet pour bien souligner que l’interprétation Doppler n’était pas la bonne. Mais si on le souhaite, on peut bien sûr définir une sorte de « vitesse », mais je trouve qu’utiliser le terme est un peu confusant. Il s’agirait plutôt de la dérivée temporelle d’une distance (disons la distance propre entre deux galaxies), mais qu’il ne faut pas interpréter comme « la vitesse d’un truc matériel mesuré dans un référentiel ». Et dans ce cas, si on dit que c’est « juste » la dérivée temporelle d’une distance, alors aucun problème à dépasser la vitesse de la lumière.
Il y a un autre exemple classique de ce phénomène : imaginez un laser très puissant tournant à 1 radian par seconde, et tellement puissant qu’on observe la tâche lumineuse qu’il produit sur un mur à 600 000 km de là. La tâche lumineuse se déplacera sur le mur à une « vitesse » de 600 000 km/s. Pour autant on n’entre pas en contradiction avec la relativité restreinte. Cette « vitesse » est la dérivée temporelle d’une distance, mais pas la vitesse de propagation d’un bout de matière ou d’énergie mesurée dans un référentiel.
9 Comments
Je pense que le fait de traiter des sujets en plusieurs vidéos est une bonne chose, car comme il y a forcément un intervalle de temps entre chaque production, on a le temps de comprendre la première avant d’attaquer la deuxième.
En passant, merci beaucoup pour votre travail depuis plus d’une décennie.
Une petite question cependant. La vitesse d’expansion augmente donc actuellement. Cependant, peut-elle baisser un jour ?
Merci encore pour votre travail et votre réponse.
« Bon, ben y’a plus qu’à ! » : bravo pour cette pointe d’humour au milieu de considérations scientifiques très poussées.
Tout à fait remarquable, comme d’habitude lorsque vous traitez ce type de sujet.
Merci pour ce gros travail qui éclaire l’esprit.
Cordialement
Jean
Très bonne vidéo comme d’habitude… juste une petite confusion avec le facteur z. Le décalage Doppler n’est proportionnel à v/c que lorsque v/c<<1 mais son expression relativiste est plutôt z=sqrt((1+ß)/(1-ß))-1, avec ß=v/c. On atteint donc un z=2 pour v=0.8c et z tend vers l'infini lorsque la source s'éloigne à une vitesse tendant vers c… En l'occurrence ce n'est pas le fait que z puisse prendre des valeurs arbitrairement grande qui évacue l'interprétation en termes d'effet Doppler…
Ah mais oui effectivement ! J’avais oublié cette expression de l’effet Doppler relativiste, merci du complément !
Bonsoir
J’aurais deux questions liées, sur la prise en compte ou pas de la courbure de l’univers dans les méthodes de mesure des distances et donc de l’expansion ; je me les suis posées après le visionnage des épisodes sur l’expansion et de celui tout aussi passionnant sur la mesure des distances. Également, le sujet de la tension de Hubble a été évoqué dans la presse récemment. C’est sans doute bête, mais j’aimerais bien savoir quand même.
Première question : prenons une galaxie lointaine d’où partent deux signaux lumineux : le premier nous arrive en ligne droite car l’espace-temps n’est pas déformé sur le trajet. Le deuxième nous arrive après avoir suivi une trajectoire différente, celle-ci ayant été influencée par des courbures locales de l’espace temps. Il a un trajet plus long (y compris en temps) ; l’allongement de la longueur d’onde est donc supérieur et la distance calculée de la galaxie sera différente si on se base sur les deux redshifts. La situation est la même si on mesure les distances de deux galaxies lointaines équidistantes de la terre, l’une séparée de la terre par un espace vide, l’autre par un espace avec beaucoup de matière donc courbé. L’impact de la courbure est-il pris en compte dans les mesures ou non, car peut être négligeable ?
Deuxième question : reprenons le deuxième exemple avec les deux galaxies équidistantes (d1) dans le passé avant l’expansion ; mettons nous dans un espace à une dimension (ligne) et non en trois pour simplifier :
Le trajet galaxie 1-terre était : (schéma qui ne passe pas: ligne droite) longueur d1
Le trajet galaxie 2-terre déformé était : (schéma qui ne passe pas: ligne courbée) longueur d2 = 1,5*d1
Disons que l’expansion jusqu’à maintenant a ajouté 100% à la distance.
On va avoir comme distance actuelles :
d1’= d1*2
Pour d’2, j’imagine que l’expansion ne s’applique qu’à la dimension de l’univers, donc horizontalement et pas verticalement ; peut être que la courbure est plus réduite comme la matière est la même ; la distance augmentée du fait de l’expansion est
d2’ = d2*5/3
Si on observe ces deux galaxies aujourd’hui et qu’on mesure leur distance grâce à des chandelles cosmiques, on va calculer deux couples redshift/distance si j’ai bien suivi:
d’1 avec un redshift de 2 ; c’est-à-dire 2*d1 pour un redshift de 2
d’2 avec un redshift correspondant à un allongement de 5/3 ; c’est-à-dire 2,5*d1 pour un redshift de 5/3
L’expansion calculée ne va pas être la même.
Donc s’il faut prendre en compte la courbure dans les calculs de distance, cela a l’air de fausser aussi les calculs de vitesse d’expansion.
Désolé c’est moins clair sans les dessins mais je n’ai pas pu les coller….
Je ne sais pas si vous aurez le temps de lire et répondre, mais merci beaucoup si c’est le cas !
Christian
Bonjour,
A vrai dire ce n’est pas un commentaire que je souhaite faire mais poser une question
Votre approche est très intéressante et je me demande ; l’expansion de l’univers n’entraîne-t-elle pas en même temps une expansion globale, par exemple celle du système solaire, voire de la terre elle même ?
En tous cas merci pour votre travail et l’éclairage que vous donnez à tous.
Cordialement
Yves RENAUD
Bonjour, tout d’abord merci pour ces vidéos qui abordent des sujets complexes.
je voulais poser une question à propos du laser qui tourne et la tache à 600000km : il me semble que le rayon laser ne reste pas droit puisque chaque nouveau photon qui est émis est décalé par rapport au précédent : le photon 1 est émis à 0°, 1/100 de seconde(par exemple) plus tard le 2ème photon est émis avec un angle de 360/100=3,6° par rapport au premier et ainsi de suite, on obtient donc un rayon courbé. du coup je ne suis pas sur que la « vitesse » de la tache obtenue est quand même de 600000km/s
Merci d’avance et encore bravo pour ce travail remarquable 😉
Bonjour,
Les distances exprimées dans les différents diagrammes sont elles les distances au moment de l’émission ou bien au moment de la réception du signal ?
Thomas