La vidéo d’aujourd’hui parle d’une technique puissante, dangereuse et méconnue. Non, pas le côté obscur de la Force, mais l’analyse dimensionnelle !
Comme d’habitude, quelques compléments pour celles et ceux qui veulent en savoir plus, ou qui connaissaient déjà le sujet !
Unités et dimensions
Ceux qui ont déjà fait de l’analyse dimensionnelle auront noté le choix que j’ai fait de ne pas franchement aborder le concept de « dimension », et de parler uniquement des unités. Plusieurs raisons à cela.
La première, c’est que ça m’obligeait à introduire un concept abstrait supplémentaire, à passer du temps à expliquer ce qu’il est, et ce qu’il n’est pas. La deuxième c’est qu’en pratique, je ne sais pas vous, mais moi je fais toujours avec les unités, je trouve ça plus facile et concret. Et la troisième c’est que le concept de dimension a le mauvais goût de s’appeler « dimension », qui est déjà un mot qui a un sens, mais pas le même. Je trouve ça toujours extrêmement difficile de commencer à présenter un concept portant le même nom qu’un autre en expliquant qu’on ne parle pas de la même chose. Je suis donc resté sur les unités !
J’ai expliqué vite fait que les unités à considérer comme n »fondamentales » vont dépendre du contexte. Stricto sensu ça ne devrait pas, mais en pratique si. Prenons l’exemple de la température. Si je suis dans un contexte de transfert de chaleur macroscopique, avec des conductivités, capacités calorifiques, etc. je vais traiter la température comme une dimension en soi. En revanche si je suis en train de faire de la physique statistique, température et énergie c’est pareil, via la constante de Boltzmann. D’ailleurs si on pousse un peu, tout n’est qu’énergie !
Un point confusant que m’a fait remarquer un commentaire. Le fait de parler d’unité plutôt que de dimension peut perturber notamment quand il s’agit d’angles. Les angles peuvent avoir une unité, mais cela reste une quantité sans dimension (que l’on peut voir comme un rapport de longueurs).
Tiens d’ailleurs dans Pythagore, la vraie forme de la fonction qui donne l’aire d’un triangle rectangle, ça doit être un truc du genre
\(\frac 12 x^2 \sin(\theta)\cos(\theta)\)
Le théorème de Buckingham
Pour ceux qui s’inquiéteraient que l’analyse dimensionnelle ne soit que bricolage et ne repose sur rien de solide, rassurez-vous ! Il existe un théorème, parfois nommé « le théorème \(\Pi\) », qui permet de donner un sens à tout cela, notamment en mettant en avant les quantités sans dimension que l’on peut construire à partir des variables du problème.
Reste la question de la constante sans dimension.
On peut se dire qu’il est assez rare qu’en physique les constantes soient très exotiques, mais ça arrive quand même ! Mon exemple préféré, c’est celui du calcul de la divergence à deux boucles de la quantification perturbative de la relativité générale. Ca sonne très barbare comme ça, mais c’est en gros le calcul qui montre qu’il est impossible de traiter la gravité d’Einstein de la même manière que les autres forces, quand on veut les considérer dans le cadre de la mécanique quantique (les « quantifier »). La divergence, c’est un terme qui montre que des infinis vont apparaître de manière incurable, et dans le cas que je mentionne, le terme divergent incriminé s’écrit
\(\displaystyle \frac{209}{737280}\frac{1}{\pi^4} \frac{1}{\epsilon} \int d^4x \sqrt{-g} R^{\mu \nu}_{\rho\sigma}R_{\epsilon\theta}^{\rho\sigma}R^{\epsilon\theta}_{\mu \nu}\)
Comme vous le voyez, le coefficient numérique est assez improbable ! (et en plus il est très petit) D’ailleurs ce genre de petits coefficients arrivent assez régulièrement en physique des particules à cause des \((2\pi)^D\) qui résultent des normalisations des gaussiennes en D dimensions.
Autour du pendule
Si vous avez déjà vraiment fait l’exercice du pendule, vous savez peut-être que ce que j’ai raconté n’est vrai que dans l’approximation des petits angles. Dans le cas général, l’équation devient non-linéaire et l’angle initial (une quantité sans dimension) doit être pris en compte.
Dans le cas général, la période s’exprime comme
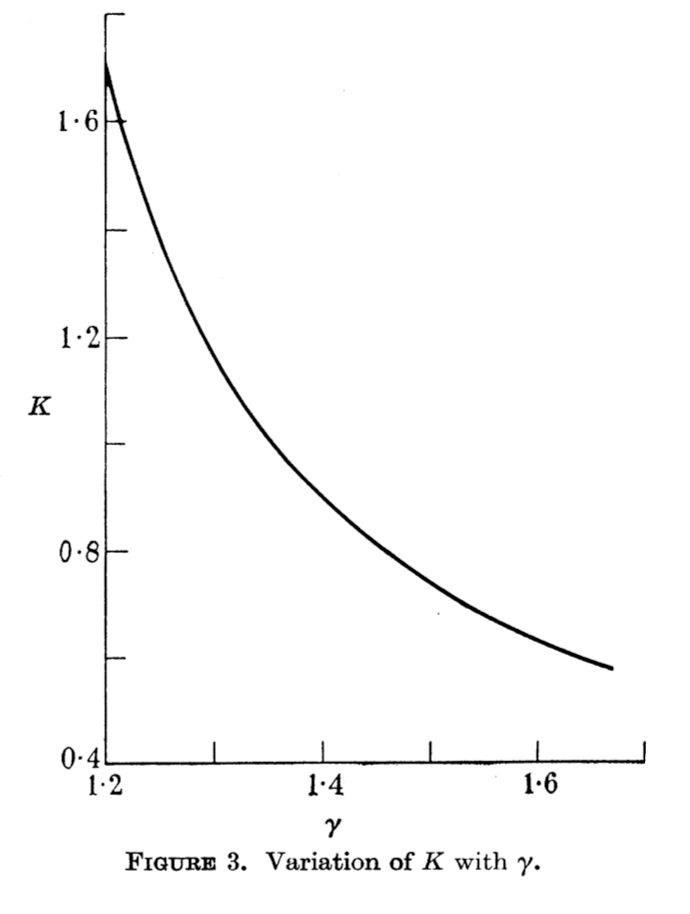
\(\displaystyle 2\pi\sqrt{\frac Lg} \frac{2}{\pi} K(\sin \theta_0)\)
où \(\theta_0\) est l’angle initial et \(K\) est la fonction elliptique de Jacobi. Bien sûr il est totalement exclu de « deviner » ça par analyse dimensionnelle !
Taylor et la bombe
Commençons par une précision intéressante concernant les images de Trinity. On peut avoir l’impression qu’il y en a un vingtaine, vu comme ça. En réalité, il y en a plus de 100 000 ! Le photographe s’appelait Berlyn Brixner. Extrait du site :
Brixner’s objective as a member of the Manhattan Project can be best described as follows: Photograph all aspects of an unknown and unpredictable event that begins with the brightest flash of light ever produced on Earth. To accomplish this, Brixner was stationed 10,000 yards (5.68 miles) away from the detonation. He incorporated fifty cameras of various running speeds using 16-millimeter black-and-white film positioned at different locations in order to capture in full and slow motion. These cameras were positioned at every possible angle, distance, and available film speed. All the cameras, including the one he had in his lap at the time of the atomic bomb’s detonation were operated from a central control station. Approximately 100,000 photographs were made of the Trinity atomic bomb test.
Comme je l’ai évoqué dans la vidéo, l’histoire de l’analyse de la puissance de la bombe par Taylor s’est retrouvée assez romancée au fil du temps. Si la question de ce glissement vous intéresse, vous pouvez consulter l’article suivant
Michael A.B. Deakin (2011) G.I. Taylor and the Trinity test, International Journal of Mathematical Education in Science and Technology, 42:8, 1069-1079, DOI: 10.1080/0020739X.2011.562324
Taylor a notamment écrit deux articles. Ils ont je crois été publié en même temps, mais le premier est « la théorie », développée avant la publication des images de Trinity, et le second est « la pratique » avec les photos de Trinity.
Taylor, Geoffrey. « The formation of a blast wave by a very intense explosion. I. Theoretical discussion. » & « II. The atomic explosion of 1945. » Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 201.1065 (1950): 159-186.
L’ensemble fait 37 pages ! Donc le travail de Taylor n’a pas consisté à juste faire une analyse dimensionnelle de coin de table. Le point essentiel est que si on fait correctement l’analyse physique du problème, on trouve que l’indice adiabatique du gaz \(\gamma\) doit jouer un rôle, or d’une part c’est une quantité sans dimension (qu’on peut donc faire apparaitre dans n’importe quelle fonction), d’autre part il est connu que cet indice dépend de la température du gaz !
Dans son premier article, Taylor considère notamment le cas « idéal » de $\gamma = 1.4$, c’est-à-dire un gaz parfait diatomique. Dans le second article, il regarde comment ça colle avec les images de Trinity, et se rend compte, ô surprise, que l’approximation $\gamma = 1.4$ fonctionne tout à fait bien. Ca n’était pas du tout garanti, puisque le gaz s’échauffe dans l’explosion, et que cela fait baisser le coefficient adiabatique.
Autre petit miracle, pour la valeur de $\gamma = 1.4$, la constante est très proche de 1, ce qui fait que l’analyse dimensionnelle semble marcher si bien.






20 Comments
Bonjour. J’attire votre attention sur une publication de Jean Lahérrere qui a corrélé certaines des distributions que vous présentez avec ce qu’il appelle des « fractales paraboliques ».
Voici ce qu’il en dit récemment
« “Distributions de type fractal parabolique dans la Nature”- Comptes Rendus de l’Académie des Sciences- T.322 -Série IIa n°7-4 Avril 1996 p535-541 http://www.oilcrisis.com/laherrere/fractal.htm, je montrais que les galaxies, les agglomérations urbaines, les tremblements de terre et les réserves pétrolières suivent une distribution fractale parabolique (et non pas linéaires comme la loi de Gutenberg-Richer) » »
Merci pour votre travail.
Erreur de post (mauvaise video!)
E = 19 000 000 kg de TNT = 19 kt de TNT
En effet je me suis planté !
Merci pour ce post mais j’ai du mal à être convaincu par la preuve du théorème de Pythagore.
Pourquoi l’on suppose que la fonction f ne dépend pas de x?
Après tout on pourrait avoir: f(θ, x) = cos(θ) si x<1 et f(θ, x)=sin(θ) sinon (ou toute autre atrocité).
Une fonction du genre $\cos(\theta)$ ne peut pas marcher car elle serait sans dimension, donc ça ne peut pas donner une surface à la fin.
Merci pour la réponse mais je parlais de la partie notée f en vidéo, à savoir ce qui suit le x².
Dans la vidéo, il est affirmé que l’aire est de la forme x² f(θ) et je me demandais pourquoi on ne pouvait pas avoir x² f(θ, x) où f(θ, x) est bien adimensionnel mais dépend de x
Je pense que l’important pour comprendre la non dépendance à x de la fonction f c’est qu’un triangle rectangle est *caractérisé* par une longueur et un angle (précisé au tout début de la démo: « suffisent à complètement décrire le triangle rectangle » ).
La fonction f se doit d’être adimensionnelle.
Or il est impossible pour cette fonction de dépendre de x sans faire intervenir une autre longueur indépendante de x (par analyse dimensionnelle). Ce qui briserait la caratérisation du triangle rectangle par le couple theta et x.
Ton exemple est trompeur car dans « f(θ, x) = cos(θ) si x<1 sinon ..", x<1 n'a pas de sens dimensionnellement (1 est sans dimension). Il faut comparer x avec une autre longueur, on est donc bien dans le cas précédent.
J'espère que mon explication est la bonne et qu'elle est relativement claire!
Oui c’est exactement ça ! Il y a d’ailleurs un cas où cette démo de Pythagore ne marche pas précisément pour cette raison, c’est pour un triangle en espace courbe. Car là il y a une longueur supplémentaire, le rayon de courbure de l’espace qui intervient, et qui permet de fabriquer une quantité sans dimension et donc autorise plein de formes de la fonction
On peut se convaincre que $f(\theta)$ ne dépend pas de $x$ par un calcul élémentaire.
L’aire du rectangle obtenu par collage de deux triangles rectangles de paramètres $(x,\theta)$ est proportionnelle à $x^2$, et on note que la constante de proportionnalité est nécessairement indépendante de $x$. Il existe donc une fonction $g$ telle que, en notant $T(x,\theta)$ l’aire de ce rectangle, on ait
\begin{equation}
T(x,\theta) = x^2 * g(\theta).
\end{equation}
Or $T(x,\theta) = 2 A(x,\theta)$, il vient donc immédiatement que pour tout $x$,$\theta$, on a
\begin{equation}
A(x,\theta) = x^2 A(1,\theta)
\end{equation}
En posant $f(\theta) = A(1,\theta)$, on a
\begin{equation}
A(x,theta) = x^2 f(theta)
\end{equation}
et $f$ ne dépend pas de $x$.
Bonjour , merci pour votre vidéo et votre commentaire .
3 points :
1/ OUI , il faut absolument répéter que l’ Analyse Dimensionnelle (AD )est « locale » : elle se pratique sur les équations du problème considéré posées . La réduction utilise alors le SUN ( système d’unités naturelles ) DU problème considéré , et cela peut agrandir le nombre des unités : ce fût l’objet du débat Rayleigh-Riaboushinski . Une fois compris ce caractère local ( càd adapté à chaque système d’équations ) , l’ AD peut se résumer à : sans restriction de généralité( srg ) , on peut poser h-barre = 1 , m = 1 , c = 1 , etc . Claude.Cohen-Tannoudji en avait discuté avec Pierre-Gilles deGennes , afin de savoir si , les équations étant posées , il fallait ou non , les écrire de façon simplifiée , et comment procéder avec des étudiants : la réponse fût nuancée : ça dépend ! sourire ! Réduire l’écriture par les SUN fait ressortir la structure algébrique du pb ; mais lors d’une première approche des calculs , l’homogénéité aide comme garde-fou précieux.
2/ la remarque de J.A.Wheeler : dans le « bon » SUN adéquat, tout résultat est de l’OdG de 1 , ou alors il faut se poser des questions : cela est discuté abondamment par JM Levy-Leblond , et son analyse est tout à fait pertinente . Si c^4/G est une « unité de puissance » légitime pour les trous noirs , il n’est pas évident que le nb d’Avogadro stellaire ( hbar. c/ Gm^2 ) ^3/2 soit à la puissance 3/2 , etc ,etc
3/ Barenblatt ( école de Kolmogorov ) va plus loin :son analyse du Reynolds^ (alpha) et la notion « de l’asymptotique intermédiaire » est très puissante . La discussion faite par S.Fauve (cours de l’ens paris ) est pertinente
merci , respectueusement , marc.s
Un témoignage plutôt qu’une contribution scientifique. J’étais élève-ingénieur dans les années 70 et j’étudiais de façon assez approfondie la mécanique des fluides. Mes profs de l’époque ne parlaient pas d’analyse dimensionnelle, mais avaient 2 obsessions qu’ils voulaient faire partager à leurs étudiants : contrôler l’ordre de grandeur du résultat d’un calcul numérique et vérifier l' »équation aux dimensions » du résultat littéral. L’acquisition de cette discipline intellectuelle simple reste valable à vie et évite pas mal de déboires professionnels.
Merci David d’œuvrer à en convaincre le jeune public, et merci pour vos vidéos que je déguste avec toujours autant de plaisir.
Bonjour,
encore merci pour ça (j’ai apprécié la preuve de Pythagore)
Sinon j’ai essayé d’appliquer (naïvement) cela avec la loi de Newton, mais je n’y arrive pas : F = K.m.m’/R^2
j’ai l’impression que K (i.e. G) n’est pas sans dimension, c’est bien cela la raison ? ou suis passé à coté de qqchose ?
et oui… ce sont des newton mètre carré par kilogramme carré !
Bonjour,
Merci pour cette vidéo, je ne connaissait pas l’analyse dimensionnelle.
Je ne comprends pas en revanche comment celle-ci peut donner une estimation de la réponse.
Ici on semble pouvoir trouver une formule juste en manipulant les variables, mais ne pourrait pas tomber sur des cas où on a une constante très grande ou très petite que l’on devrait ajouter à la formule, ce qui fausserait les résultats ? Est-ce que ça ne dépend pas fortement du Système International des unités ?
D’autre part est-ce que cette vérification est vraiment efficace ? Par exemple la formule E = mc² relie une masse et une énergie. Avec la méthode utilisée dans la vidéo on cherche déterminer une énergie E en joules à partir d’une masse m en kg et une constante en m²s-², les unités ne correspondent pas.
Bonjour,
L’analyse dimensionnelle permet de retrouver quelques formules simples en physique mais il ne doit pas y en avoir tellement que ça , non ? Car j’ai cherché sur le net d’autres exemples et je tombe toujours sur le pendule, la puissance d’une bombe, la pulsation du cyclotron , la chute des corps de Galilée.la vitesse de sédimentation et le rayon de Hubble. Et c’est tout. Quelqu’un aurait il un site qui en recense d’autres ?
Bonjour,
Une question qui n’a rien à voir mais il y avait sur le site un article qui parlait d’erreurs liées aux fluctuations statistiques (bruit gaussien) lorsqu’on essayait de prendre en compte et de corriger le paradoxe de Simpson, et qui montrait que de très nombreuses conclusions dans des articles scientifiques étaient erronées, ce qui était très grave.
Je voulais relire cet article mais il n’y est plus. Il a été supprimé ? Pourquoi donc ?
Bonjour, vidéo passionnante, comme toutes les vidéos de la chaîne !
Juste une petit remarque sur la formule du pendule. C’est vrai qu’elle n’est valable que pour les petits angles. Mais le rayon R de la boule a également une influence ! S’il est de l’ordre de la distance entre le point d’attache et le centre de la boule (L), la période diminue à cause du moment d’inertie de la boule par rapport à son centre qui devient non négligeable. La formule correcte (dérivée de la formule pour un pendule physique) est alors :
T = 2π √((MLL + (2/5)M RR) / (MLg))
Pingback: L’analyse dimensionnelle, ou comment se faciliter les équations en physique - vivreaulycee
Voir aussi ce livre : Dimensional Analysis and Theory of Models – January 1, 1951
by Henry L. Langhaar (et aussi sa traduction en français par C. Charcosset)