Je pourrais probablement écrire une tonne de précisions pleines d’équations pour cet épisode, je vais essayer de me limiter. Et pour les curieux, une saveur de la démonstration des inégalités de Bell se trouve à la fin du billet !
Les citations d’Einstein
Tout le monde le sait, les citations d’Einstein c’est un truc très casse gueule ! Il fallait forcément que j’en glisse quelques unes. Heureusement un livre récent d’Adam Becker, What is real ?, très bien documenté et sourcé, permet de s’y retrouver là-dedans. Einstein aurait bien dit « Dieu ne joue pas aux dés », pas à Bohr en 1927 mais dans une lettre à Max Born du 4 décembre 1926. La citation que j’ai donnée plus tard date de 1942, dans une lettre à Lanczos.
Il existe un autre « élément de langage » fameux d’Einstein, c’est le « spooky action at a distance ».
I cannot seriously believe in it because the theory cannot be reconciled with the idea that physics should represent a reality in time and space, free from spooky actions at a distance. (Lettre à Born du 3 Mars 1947)
Je ne l’ai pas mentionné dans la vidéo, notamment parce que cette citation n’a pas de version populaire en français. J’ai l’impression que c’est dû à la difficulté de traduire ici le sens de spooky. C’est un truc à mi-chemin entre « inquiétant », « fantomatique », « qui fait peur », « effrayant », « qui donne la chair de poule ».
Mais de fait, et dommage pour Einstein, les expériences d’Alain Aspect montrent bien qu’il existe une « spooky action at a distance ».
L’argument EPR
Une des raisons qui font que l’argument EPR d’Einstein n’a pas été reçu à l’époque avec la force qu’il mérite, c’est peut-être qu’il n’était pas si clairement exposé que ça. La légende dit que le papier a été écrit par Podolsky, et si vous essayez de le lire…il n’est pas si bien écrit que ça !
Et surtout, il n’est pas dans la forme « moderne » que je vous ai présentée. Il fait référence à l’impulsion de particules qui ont été en interaction, et il semble que l’argument ait été pris parfois comme une « attaque » contre le principe d’incertitude d’Heisenberg, plus qu’une contestation de l’interprétation de Copenhague.
La forme « moderne » est due à David Bohm, qui a reformulé l’argument EPR avec deux spins intriqués, et la version que je vous ai présentée est la même, avec deux photons. Il existe une petite différence entre les spins et les photons, c’est que les photons intriqués en polarisation qui sont émis par la source dont j’ai parlée (une source de photons uniques en polarisation circulaire) sont corrélés (état superposé ++ et – -), alors que dans l’exemple classique de Bohm, les spins sont anticorrélés. L’état typique est une superposition de +- et -+. Ca ne change bien sur rien à l’argument, c’est juste un chouilla moins clair car il y a une gymnastique à faire en plus.
Qu’est-ce qu’un état intriqué ?
Un mot sur le concept même d’état intriqué. Tous les états qui par exemple superposent les 4 possibilités ne sont pas nécessairement intriqués ! Ce qui définit l’intrication, c’est la « non-factorisabilité » (je ne sais pas si le terme existe). Imaginez deux photons chacun dans un état superposé, et indépendants.
\( \Psi_1 = a\Psi_+ + b\Psi_- \\ \Psi_2 = c\Psi_+ + d\Psi_-\)
On peut fabriquer l’état complet « produit » du système :
\(\Psi_1\otimes\Psi_2 = ac(\Psi_+\otimes\Psi_+) + ad(\Psi_+\otimes\Psi_-) + bc(\Psi_-\otimes\Psi_+) + bd(\Psi_-\otimes\Psi_-)\)
Ca a l’air d’être un état intriqué, qui superpose les 4 possibilités, mais le fait que cet état se « factorise » fait qu’il n’est justement pas intriqué. Les deux particules se comportent de façon indépendante.
Alors qu’un état comme celui dont on a parlé dans la vidéo est justement un état non-factorisable en un produit de deux états, un pour chaque photon.
Polariseurs et prédictions de la mécanique quantique
Quand dans l’expérience EPR, on a deux polariseurs séparés d’un angle \(\theta\), la mécanique quantique nous dit que les probabilités de résultats identiques (++ et – -) sont de \(0.5\cos^2 \theta\) et pour les résultats différents (+- et -+) c’est \(0.5\sin^2 \theta\). La somme des 4 possibilités fait bien sûr 1. Voilà comment remplir le tableau pour n’importe quel réglage.
Un point intéressant avec cette prédiction, c’est que les valeurs numériques sont exactement celles qu’on obtient en superposant deux filtres polariseurs avec un angle \(\theta\) entre eux. Et ça n’a rien d’évident a priori, puisque les deux situations sont différentes ! Dans un cas, un même photon traverse deux filtres (et on sait qu’il est affecté par le passage du premier), et dans l’autre deux photons jumeaux traversent chacun un filtre.
J’ai hésité à le mentionner, c’est parfois présenté comme une illustration des inégalités de Bell, mais c’est un abus de langage. Il se trouve que oui, les valeurs numériques sont les mêmes, mais ça reste deux expériences différentes. Alors finalement je n’ai pas insisté, je me suis dit que ça créerait plus de confusion qu’autre chose.
Une théorie « naïve » à variables cachées
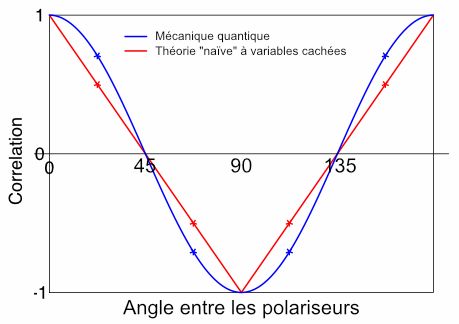
Un exercice amusant que l’on peut faire, c’est d’essayer quand même de trouver une théorie à variables cachées. Une tentative naturelle, c’est d’imaginer que chaque photon est dans un état bien défini caractérisé par un certain angle \(\lambda\), qui est la « variable cachée », et que le photon traversera tout filtre dont l’angle est suffisamment proche de l’angle \(\lambda\), par exemple dans l’intervalle \(\lambda-45°, \lambda+45°\), et tandis qu’il sera absorbé par tout filtre dont l’angle est dans l’autre intervalle.
Ce qui est intéressant de constater, c’est qu’un tel modèle à variable cachée respecte bien évidemment l’inégalité de Bell. Mais dans le tableau, il prédit 12.5% là où il y avait 7% dans la vidéo, et donc il satisfait « pile-poil » l’inégalité. (Il la sature).
On voit ci-dessous le tracé des corrélations prédites par la mécanique quantique (en bleu), et celles prédites par la théorie naïve. On voit que ça ne colle pas, et l’écart est maximum pour les angles 22.5, qui sont les angles où chercher la violation maximale des inégalités de Bell.
Les sources de photons
Parlons un peu des sources de photons. Tout d’abord au tout début, dans mon exemple à « 1 photon », je n’ai pas vraiment décrit ce qu’était cette source mystère. Pour avoir le bon état superposé, il faut s’imaginer que c’est une source de photons uniques polarisés circulairement.
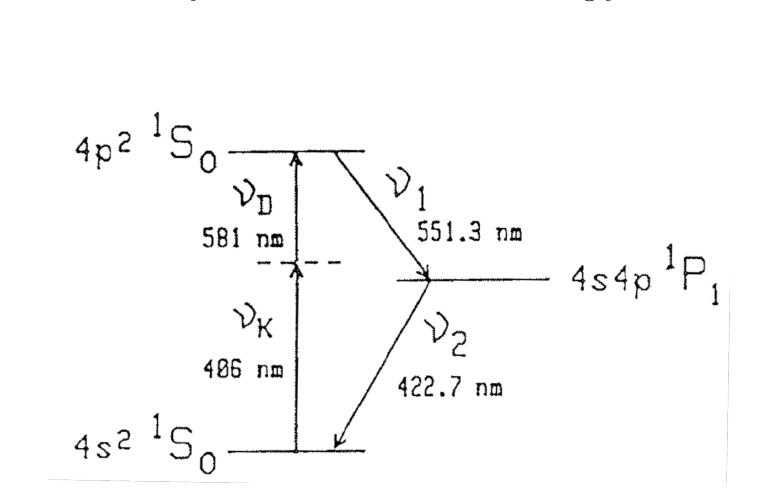
Quant à la source « réelle » utilisée par Alain Aspect, c’est à la base la même que Clauser, mais au lieu d’exciter les atomes de façon un peu aléatoire (avec une lampe UV), ce qui crée beaucoup d’états excités qui ne sont pas celui que l’on veut, Alain Aspect a utilisé une excitation laser qui permettait avec une absorption à deux photons d’arriver pile dans l’état excité, et donc d’améliorer beaucoup la pureté du signal.
On le voit ci-dessous, on amène l’atome dans un état excité par l’absorption successive de deux photons, qui doivent êtreà la bonne longueur d’onde, d’où l’utilisation de lasers accordés comme il faut.
Statistiques
Je n’ai pas forcément beaucoup insisté là-dessus, mais la violation des inégalités de Bell est une violation statistique. Ca se voit dans mon exemple où je dis que je prends 100 paires de photons. Quand je dis qu’il ne peut pas y en avoir plus que 7 dans la case « passe à 0 et est absorbé à 22.5 ». C’est évidemment 7 en moyenne. Si ça se produit avec 100 photons ça peut être une anomalie statistique. Si ça se produit avec 100 000, ça devient déjà beaucoup plus significatif !
Il existe un très bel exemple d’une violation des inégalités de Bell qui n’a pas besoin de corrélations statistiques. C’est une idée que l’on doit aux physiciens Greenberger, Horne et Zeilinger, qui ont montré que si on intriquait 3 particules (un mélange de +++ et – – -), on pouvait mesurer une certaine propriété qui d’après la mécanique quantique donne toujours un résultat +1, mais d’après toute théorie à variable cachée donne toujours un résultat -1. Donc il suffit (en théorie) d’une expérience sur un seul triplet de photons pour violer les inégalités de Bell !
https://en.wikipedia.org/wiki/Greenberger–Horne–Zeilinger_state
Pour un autre exemple d’une violation très élégante des inégalités de Bell, il y a l’état de Hardy dont j’avais parlé dans ma vidéo sur les « gâteaux quantiques ».
Echappatoires
Je n’ai pas trop commenté sur les autres échappatoires qui ont subsisté après le travail d’Alain Aspect. Il y en avait notamment une qui concernait l’efficacité des détecteurs. Pour être certain qu’une conspiration n’existait pas, il fallait des détecteurs de photons qui aient une efficacité supérieure à 70%. Ce qui a été fait par la suite.
En théorie, il existe encore des échappatoires ! Par exemple celle du superdéterminisme, qui dit que tout est absolument prévu d’avance, et que l’expérience que je vais faire, les choix des réglages etc. est absolument calculé dès le départ pour donner ces résultats là, et donc sans avoir besoin d’invoquer de l’action instantanée à distance. Mais bon le problème avec cette idée là, c’est qu’elle remet même en cause l’idée de faire de la physique pour essayer d’y comprendre quelque chose ! N’importe quel résultat expérimental violant n’importe quelle loi physique peut s’expliquer en invoquant un superdéterminisme.
Autre échappatoire aux inégalités de Bell : les mondes multiples. Il existe une hypothèse implicite (qui semble naturelle) dans le travail de Bell : on suppose que chaque mesure ne donne qu’un résultat à la fois. Si on lève cette restriction, on tombe sur l’interprétation des mondes multiples d’Everett, qui permet à la fois d’expliquer les corrélations observées en mécanique quantique, tout en préservant la localité.
Et la relativité restreinte là-dedans
Il y a une question que j’ai un peu esquivée, c’est celle de savoir comment ces résultats sur l’intrication quantique affectent la théorie de la relativité.
Il est bien sûr faux de dire que grâce à l’intrication quantique, on peut communiquer à distance de façon instantanée. L’intrication ne peut pas être utilisée pour envoyer instantanément des messages et permettre des paradoxes temporels.
Néanmoins, évacuer le problème en disant « pas de messages, pas de problèmes » me parait également un peu exagéré. D’après la version la plus aboutie du théorème de Bell, l’intrication quantique permet de violer la « causalité locale », ça n’est quand même pas rien. Certes on ne peut pas détourner ce phénomène à notre profit, mais ça reste une violation de la localité quand même, donc on a une forme de contradiction avec la relativité restreinte (même si encore une fois ça ne fout pas tout en l’air).
Comment démontrer les inégalités de Bell ?
Quand j’ai entendu parler pour la première fois des inégalités de Bell, ça m’a fait le même effet que quand j’ai découvert le théorème de Gödel. Comment est-il même possible de démontrer un truc pareil ? Comment un tel résultat peut-il être accessible à la démonstration ?
Je ne vais pas détailler toutes les étapes, mais je vais essayer de vous en donner une saveur. Pour démontrer l’inégalité de Bell, on a besoin de quelques définitions, de quelques lignes de calcul algébrique sans grande subtilité, et d’UN argument qui contient toute la physique du truc. Je vais vous donner les définitions et l’argument, je vais zapper quelques calculs.
Prenons le dispositif générique dont on a parlé : deux mesures en deux points distants A et B de l’espace, avec deux réglages possibles pour chaque : on va appeler \(\alpha\) le réglage en A, et dire qu’il peut prendre deux valeurs (\(\alpha=0\) ou \(\alpha=1\) par exemple, mais ça n’a aucune espèce d’importance), et \(\beta\) le réglage en B. Chaque mesure peut donner soit le résultat +1, soit le résultat -1. On va appeler \(a\) le résultat d’une mesure en A, et \(b\) le résultat d’une mesure en B.
Souvenez vous du tableau de la vidéo : il avait 16 cases car 4 réglages possibles, et 4 résultats possibles :
\((a=+1,b=+1), (a=+1,b=-1), (a=-1,b=+1),(a=-1,b=-1)\).
On s’intéresse de façon générale à la probabilité, quand on réalise un run de l’expérience, d’obtenir le résultat \((a,b)\) sachant qu’on a réglé les appareils sur les réglages \((\alpha,\beta)\). C’est une probabilité conditionnelle, on va la noter :
\(p(a,b|\alpha,\beta)\).
Petite définition qui nous servira ensuite : on va s’intéresser, pour un réglage donné de l’expérience, à la corrélation qu’on obtient entre les mesures de chaque côté. C’est un truc assez simple que j’ai écrit vite fait dans la vidéo : c’est la somme des probabilités des cas identiques moins la somme des probabilités des cas différents :
\(C = p(+ +) + p(- -) – p(+ -) – p(- +)\).
Et je vous laisse vous convaincre que c’est la même chose que d’écrire
\(C(\alpha,\beta) = \sum_{a,b=\pm1} ab p(a,b | \alpha,\beta)\).
Alors laissons la corrélation de côté 5 minutes, et revenons à la probabilité conditionnelle. Imaginons qu’il y ait effectivement des variables cachées qui pour chaque run de l’expérience prédéterminent le résultat. On va noter \(\lambda\) ces variables cachées : à chaque run de l’expérience, on va avoir un nouveau \(\lambda\). Je ne dis pas exactement ce qu’est \(\lambda\), ça peut être un truc très compliqué dans un espace très grand, mais la seule chose dont j’ai besoin, c’est que c’est une variable aléatoire sur un certain espace \(\lambda \in \Lambda\), avec une distribution de probabilité \(\rho(\lambda)\).
Je peux décomposer ma probabilité conditionnelle de départ avec les valeurs des variables cachées :
\(p(a,b|\alpha,\beta) = \int_{\Lambda} d\lambda\ \rho(\lambda) p(a,b|\alpha,\beta, \lambda)\)
Pour l’instant je n’ai rien écrit de révolutionnaire : j’ai juste appliqué les probabilités conditionnelles. Et maintenant, voici la clé : si la causalité locale est respectée, ce qu’il se passe en A ne peut dépendre que de \(\alpha\) et de \(\lambda\), et ce qu’il se passe en B ne peut dépendre que de \(\beta\) et de \(\lambda\).
On peut alors factoriser les probabilités :
\(p(a,b|\alpha,\beta, \lambda) = p(a|\alpha, \lambda) p(b|\beta, \lambda)\)
Voilà, c’est ça la seule ligne du raisonnement où on écrit un truc non-trivial, et qui contient toute l’essence de la démonstration. Et une fois qu’on est là, c’est seulement de la cuisine algébrique. Tout l’argument tient dans l’affirmation précédente. Je vous fais quand même un bout de la cuisine.
Reprenons ma définition de la corrélation, et injectons-y la décomposition que je viens de faire, on a alors
\(C(\alpha,\beta) = \int_{\Lambda} d\lambda \rho(\lambda) \sum_{a,b=\pm1} ab p(a|\alpha, \lambda) p(b|\beta, \lambda)\)
que l’on peut factoriser en
\(C(\alpha,\beta) = \int_{\Lambda} d\lambda \rho(\lambda) \left(\sum_{a=\pm1} a p(a|\alpha, \lambda)\right)\left(\sum_{b=\pm1}b p(b|\beta, \lambda)\right)\)
que l’on peut récrire
\(C(\alpha,\beta) = \int_{\Lambda} d\lambda \rho(\lambda) {\cal A}(\alpha,\lambda) {\cal B}(\beta,\lambda)\)
en définissant \({\cal A}\) et \({\cal B}\) comme il faut, c’est à dire la valeur moyenne obtenue pour un réglage donné sachant que la variable cachée vaut \(\lambda\).
Avec ça, on a plus qu’à construire la quantité :
\({\cal I} = C(0,0) + C(1,0) + C(0,1) -C(1,1)\),
transformer chaque \(C(,)\) en son expression intégrale :
\({\cal I} = \int_{\Lambda} d\lambda \rho(\lambda) \left[{\cal A}(0,\lambda) {\cal B}(0,\lambda) + {\cal A}(1,\lambda) {\cal B}(0,\lambda) + {\cal A}(0,\lambda) {\cal B}(1,\lambda) – {\cal A}(1,\lambda) {\cal B}(1,\lambda)\right]\)
faire une ou deux manipulations sous l’intégrale pour démontrer la borne :
\(|{\cal I}| \leq 2\).
Un point assez subtil de l’argument : ici, on n’a PAS supposé le déterminisme, juste la causalité locale. Ajouter l’hypothèse du déterminisme, ça reviendrait à dire que pour une valeur donnée de la variable cachée \(\lambda\), et pour un réglage donné \(\alpha\), la probabilité \(p(a | \alpha, \lambda)\) vaut 1 pour une valeur de \(a\) et 0 pour l’autre (et que par conséquent \({\cal A}(\alpha, \lambda)\) vaut +1 ou -1. Mais en fait, rien dans l’argument n’oblige à ça ! On peut tenir ce raisonnement même en l’absence de déterminisme.
Autre point, il y a en fait 4 inégalités de Bell. J’ai construit la quantité \({\cal I}\) en mettant un signe négatif devant le terme 1,1, mais j’aurai pu choisir n’importe lequel des 3 autres termes, puisqu’ils jouent un rôle symétrique.






116 Comments
« que le photon traversera tout filtre dont l’angle est suffisamment proche de l’angle λ, par exemple dans l’intervalle α−45°,α+45°, »
Je suppose que c’est plutôt λ – 45° et λ+45° ?
Ah oui mince j’ai changé les notations en cours d’écriture et je n’ai pas tout corrigé !
Hello,
Oui, c’est probant a partir de l’hypothèse du concept corpusculaire de la lumière et de la construction très « mathématique et statistique » de la physique quantique ( dont je respecte complètement l’utilité).
Disons tout de suite que j’aimerais consolider ces résultats avec une approche ondulatoire des phénomènes lumineux pour être convaincu de cette « preuve » de l’intrication.
Ah ! mon ancêtre devait être saint Thomas, et encore, je réfuterais sa sainteté…
Si les expériences de Clauser et de l’autre (j’ai entendu HallTapkinkin dans la vidéo mais c’est pas ça :D) à Harvard renvoyaient des résultats différents mais qu’un doute était permis à cause de l’intervalle de fluctuation trop grand, pourquoi ne pas répéter l’expérience un grand nombre de fois ?
C’était Holt et Pipkin. Eh bien l’expérience durait déjà des jours et des jours !
Et puis ce que voulait surtout faire Alain Aspect, c’est la modification avec les polariseurs qui changent en vol !
Pourquoi la source de lumière a mis 5 ans a être créé ? Quelques sont les étapes que Alain ASPECT a effectué pendant ces 5 ans ? J’ai du mal à comprendre ce qui a pu être amélioré petit à petit dans la création de cette source.
C’est le fait de passer d’une excitation « désordonnée » (comme le faisait Clauser) à une excitation précise, grâce à des phénomènes non-linéaires et l’absorption conjointe de deux photons.
Et du coup est-ce que c’est quelque chose qui a été trouvé d’un coup au bout de 5 ans « par hasard » en testant pleins de choses ou est-ce que Alain Aspect avait déjà une idée de comment résoudre ce problème au début des 5 ans ?
Comment c’est possible d’envoyer un proton dans une direction ou une autre suivant la polarisation mesurée ? Est-ce que c’est justement grâce a la cuve acoustique dont on parle plus tard ?
On parle de photons, pas de protons.
On utilise des cristaux biréfringents (indices optiques différents selon l’orientation de la polarisation incidente), qui permettent de séparer spatialement la lumière suivant sa polarisation.
La cuve acoustique permet simplement de choisir vers quel polariseur on envoie les photons.
(Dans cette expérience, polariseur = cristal biréfrigent.)
Rien à voir mais si je ne devais acheter qu’un seul livre entre Mais qui a attrapé le bison de Higgs et Insoluble mais vrai, lequel devrais-je choisir ? Sachant que j’ai vu toutes les vidéos / lu tout les billets de blogs.
Cela fait 6 ans que j’attend cette vidéo (https://scienceetonnante.com/2015/03/23/le-libre-arbitre-existe-t-il-video/#comment-7253) et j’étais donc super heureux quand j’ai vu le titre de la nouvelle vidéo. Mais au vu de la fin de la vidéo, finalement la question du déterminisme n’est pas encore tranchée.
J’ai du mal à comprendre ce qu’est une variable cachée globale / non locale, mais je suppose que je devrais attendre l’épisode De Broglie Bohm pour en savoir plus 🙂
Peut être dans 6 ans à nouveau :p
le superdéterminisme n’empêche pas de faire de la physique. il montre le biais de sélection. nous faisons partie du système observé. les inégalités de Bell avec le principe de causalité questionnent de manière scientifique l’a priori de libre-arbitre. il y a un siècle et demi on pensait l’humain séparé des animaux. il y a un demi-siècle on pensait tous les organes plastiques sauf le cerveau…. pourquoi notre esprit serait-il différent des autres mécanismes physiques? Attention ce n’est pas de l’explication anthropocentrée. C’est juste pour relevé le gros biais de sélection, comme quand on ne remarque quel type de file on a pris au supermarché que lorsque qu’on a pris la mauvaise…
Bonjour,
Je pense que la phrase « empêche de faire de la physique » veut simplement dire que si l’on accepte l’hypothèse du superdéterminisme, alors il est vain de chercher des règles qui s’appliquent au monde physique. En effet, toujours sous hypothèse d’hyperdéterminisme, il est tout à fait possible que 1 fois tous les 6 milliards d’années, la gravité terrestre s’inverse brutalement et nous nous retrouvons tous propulsés dans l’espace (par exemple). Et nous n’avons absolument aucun moyen de prédire un tel événement ou tout autre plus farfelu encore.
Autrement dit, pour pouvoir « faire de la physique », il faut au moins admettre la possibilité d’établir des lois qui sont universelles dans le temps et l’espace. Cela alors même que l’on n’a accès qu’à un tout petit bout de temps et d’espace.
désolé, pouvez-vous préciser le passage « Ajouter l’hypothèse du déterminisme, ça reviendrait à dire que pour une valeur donnée de la variable cachée λ, et pour un réglage donné α, la probabilité p(a|α,λ) vaut 1 pour une valeur de a et 0 pour l’autre (et que par conséquent A(α,λ) vaut +1 ou -1. « $
vous parlez de superdéterminisme/éternalisme? ou de déterminisme « simple » ?
je n’ai pas les capacités pour parler de ce sujet. mais je trouve ce lien https://www.futura-sciences.com/sciences/dossiers/physique-causalite-classique-remise-question-physique-quantique-3/page/2/ assez précis sur le sujet.
En langage familier, c’est comme si on voulait voir la solidité d’un bâton en essayant de la plier. Il plie ou non. Mais tout ceux étudiés n’avaient pas la même résistance. Nos mesures impliquent une interactions, et « binarisent » nos sujets d’études, parce qu’il nous est impossible de connaître les états intermédiaires.
Bonjour David, merci beaucoup pour votre vidéo très intéressante et pour les maths derrière les inégalités de Bell.
Cependant, si je ne dis pas de bêtises, il me semble que la théorie des mondes multiples (due à Everett si je ne m’abuse) « résout » la notion de hasard fondamental et évite également de postuler qu’il y a une réduction du paquet d’onde lors d’une mesure. Au passage, s’il y avait réduction du paquet d’onde, ce phénomène serait l’unique phénomène de la mécanique quantique à la fois non linéaire, non unitaire et discontinu (et qui ne respecte pas la symétrie CPT je crois). Qu’en pensez-vous ?
Oui c’est juste, une autre échappatoire c’est d’invoquer des univers multiples !
Je vais faire un petit ajout à ce sujet
Salut.
passionné, je revisionne la vidéo pour bien comprendre.
Je bloque sur deux définitions importante pour une entière compréhension:
celle de non localité ou j’ai une vague compréhension.
Et celle de variable caché ou je patauge pas mal.
T’a bien vulgarisé mais ça reste quant même réservé aux passionnées de physique.
Merci.
Je me répond.
Pour le coup en revisionnant j’ai fini par comprendre.
Il y a encore deux ou trois détailles qui m’échappent.
je pence qu’il est possible de remettre en cause un des concept de la physique quantique.
Le concept de particule « non déterminer a l’avance » ou dis autrement « la dualité » d’une particule.
Allé je continue.
le vocabulaire Technique ne fais qu’obscurcir le tableau et rend confus l’auditeur.
Pourquoi utiliser le mot « localité » a la place « d’influence instantané »?
Ces mots n’ont absolument pas le même sens pour un novice.
Puis pourquoi parler de « variable caché 16:15 » plutôt que de parler de « Photons déterminer a l’avance » qui est le cœur du débat. Les Particules sont elle déterminer avant la mesure?
Quant j’arrive a 17:38 Je suis complètement larguer avec un vocabulaire complètement décalé de la réalité.
J’écris mot pour mot se que t’a écrit puis je traduis dans un langage courant.
Si (1) la prédiction de la mécanique quantique sont correctes et (2) localité : Il n’y a pas d’influences instantanées a distance alors il existe des variables cachées.
Traduction.
Si (1)les prédictions de la mécanique quantique sont correct et que (2) il n’existe pas d’influence instantanée alors les Photons sont déterminé a l’avance puisque la condition (2) n’est pas respecter.
Bon, je continue le visionnage.
Bon ça y est j’ai bien cerner le problème.
Je suis pas un rapide.
J’avais déjà fais une démo dans une vidéo de Passe-science qui explique que l’inégalité de Bell ne prouve rien car elle est tout simplement contradictoire.
Pour l’ensemble des inégalités il y en a forcement une qui est fausse dans une citation déterministe.
Je vais tenter d’adapter la démo avec la vidéo de science-étonnante.
Lien: https://www.youtube.com/watch?v=7fbANQs6Tkg&lc=UgxRcJLlNwVwP4ulF6B4AaABAg&ab_channel=Passe-Science
Cordialement.
Thomas.
Salut j’ai bien avancé.
Je simule toutes les possibilités de la situation ou les Photons sont déterminer a l’avance.
Si toutes les inégalités de Bell sont dite vrais dans une situation déterministe alors aucune inégalité ne devrais être violer.
Etant donnée que toues les possibilité peuvent exister alors il y a forcement une inégalité qui est violé bien que nous sommes partie d’un System totalement déterministe donc bye bye Monsieur Bell.
Dis autrement si les inégalités de Bell sont violer pour une situation non déterminer autant que déterminer a l’avance donc ne prouve rien du tout.
Bonjour,
J’ai adore cette video, mais une question m’a taraude pendant toute la video : Sans vouloir etre farfelu, existe-t-il une theorie d’une 4eme dimension ou les photons seraient en fait une seule et meme particule ? Ainsi, cette dimension « est » la variable cachee, et la principe de localite est conserve. De ce point de vue, meme l’intrication quantique ne serait en realite que la facon dont nous percevons cette dimension.
PS: desole pour les accents, je suis sur un clavier qwerty.
Merci
Il y a cette conjecture dite « EPR=ER » qui affirme que deux particules intriquées seraient reliées par un « trou de ver » permettant la communication
David,
Avant de poser ma question, je dois vous remercier et vous féliciter pour votre travail. Je connais ce blog depuis peu. Mais j’ai déjà visionné pas mal de vidéos toutes plus intéressantes les unes que les autres. Il y a longtemps que je dévore de la vulgarisation scientifique. Mais vos vidéos m’ont vraiment fait passer un cap. On a l’impression d’être plus intelligent après les avoir vues.
Les thèmes qui me fascinent le plus sont ceux qui gravitent autour de la relativité et de la mécanique quantique.
Cette dernière vidéo était géniale. Je l’attendais en quelque sorte.
J’en viens à ma question qui me taraude de longue date. Je la poste ici car elle rejoint celle de Nicolas. C’est d’ailleurs peut-être la même.
Comme beaucoup, j’ai un peu de mal à accepter la fameuse « spooky action at a distance ». J’ai toujours pensé que des particules intriquées sont en réalité le même objet. En tout cas, je trouve que c’est la plus simple explication. Si c’était le cas, il n’y aurait aucune surprise à ce que leurs mesures donnent le même résultat.
J’imagine une sorte d’onde qui se propagerait dans d’autres dimensions pour traverser les nôtres en plusieurs endroits.
Pour simplifier, imaginons que nous vivions dans un monde en 2d sur un plan. La 3ème dimension existe mais nous ne la voyons pas. Imaginons que nous soyons capable de générer une onde dans notre plan (comme un rond dans l’eau). Cette onde serait donc un cercle grandissant. Admettons qu’il puisse être bleu ou rouge. Imaginons, encore, que ce cercle se déploie parfois dans un plan qui forme un angle avec le notre (90° par exemple). Le cercle se déploie dans l’espace et coupe notre plan en 2 points. Notre vision 2d serait celle de deux points qui s’éloignent l’un de l’autre. On appellerait ces points des particules. Si l’on pouvait les mesurer, on s’apercevrait à notre grande surprise qu’elles seraient toujours de la même couleur. Du point de vue 2d, c’est peut-être surprenant. Mais du point de 3d, pas tout puisque c’est le même objet.
Ma question fait echo à celle de Nicolas, est-ce que cette théorie a déjà été imaginée ?
Est-ce la même chose que d’être reliés par des trous de ver ?
Bien à vous
Je ne crois pas au trou de ver qui relierait deux particules, puisqu’un trou de ver par définition, est sensé relier deux singularités où l’espace-temps s’effondre (trou noir/trou blanc). Imaginer un trou de ver qui permettrait d’expliquer l’intrication quantique, c’est un peu comme essayer d’expliquer le mouvement bizarre des planètes dans la théorie géocentrique: on y arrive, mais c’est toujours tiré par les cheveux.
Je te rejoins sur ta théorie d’une dimension supplémentaire, mais si personnellement c’est assez présomptueux d’avoir des théorie avec les maigres connaissances que j’ai sur le sujet 🙂
En tant que néophyte, je ne peux que faire marcher mon imagination. Et pourquoi ne pas imaginer une dimension pour chacune des propriétés d’une particule ? Et si quand on observe deux particules intriquées, on n’observait finalement que la projection d’une seule particule, qui ait une trajectoire particulière dans la dimension qui correspond à ce que l’on perçoit nous comme la « polarité » ?
Malgré toutes les preuves indiscutables apportées par John Bell et Alain Aspect, j’ai l’intuition qu’Einstein avait encore raison – ou plutôt j’ai envie de faire confiance à l’intuition d’Einstein. Peut-être que comme pour le géocentrisme, nous n’avons pas toutes les clés pour comprendre ces phénomènes, et nous avons besoin de changer de point de vue.
Je précise que le « présomptueux » ne s’adresse qu’à moi, parce que je n’y connais pas grand chose à tout ça. Ce n’est en aucun cas un jugement sur le fait que toi aussi tu aies des théories 🙂
(je préfère préciser, en me relisant j’ai vu une double lecture possible)
bonjour,
bonne video toujours et le sujet est intéressant. J’ai qques remarques sur le raisonnement logique, je ne sais pas si elles tiennent :
1 si les prédictions de la MQ sont correctes
2 pas d’influence à distance
alors 3 la MQ est incomplète.
Prenons le point 1 comme acquis les prédictions de la MQ sont statistiquement correctes ,.
En revanche pour le point 2, on ne pourra jamais assurer en vertu du principe d’incertitudes que les 2 systèmes de mesures distants seront rigoureusement identiques donc on ne peut pas certifier (sauf en pensée ) que les mesures sur de 2 photons intriqués donneront des résultats identiques, par conséquent on ne pourra jamais conclure rigoureusement qu’il y a une action à distance, c’est le point 2 qui est non réaliste donc on ne peut pas conclure que la MQ est incomplète.
Par ailleurs, pour s’assurer que les mesures distantes sont identiques , il faudra bien les comparer localement en un endroit donné, tant que les mesures sont distantes on ne peut rien dire sur leur corrélation, et là de même on observera que localement une supposé action à distance.
J’ai d’autres remarques sur les expériences de Bell Aspect mais ce sera pour plus tard.
Bonne Journée.
Bonjour David,
Encore merci pour cette excellente video ! Je suis impatient d’avoir votre point de vue sur la vision Bohm-de Broglie, car je ne comprends toujours pas pourquoi cette voie également prometteuse, n’a jamais été plus mise en avant.
Notamment a la lumière des travaux du Dr. Couder et Eddi sur les marcheurs, et la mémoire de chemin, qui propose une analogie et des pistes de réflexions tout a fait convaincantes pour expliquer de manière plus « réaliste » des résultats fondamentaux de la physique quantique !
D’ailleurs certaines expérience tendaient a redémontrer les resultats de l’experience des 2 fentes, en savez vous plus a ce sujet ?
Bonjour David,
Excellente vidéo, comme d’habitude, merci !
Pour moi, le plus mystérieux dans toute cette histoire, c’est que 40 ans après, Alain Aspect n’ait toujours pas eu le prix Nobel…
Eh bien, voilà qui est fait, et bien mérité, bravo !
Bonjour David,
Il y a encore une petite chose que je ne comprends pas.
A 28:00 de la vidéo, on aboutit à un paradoxe quand on prend les photons (+-) de l’expérience 0°-45° et qu’on dit qu’il doivent respecter les 7% de l’expérience 0°-22.5°.
Mais ce résultat des 7% s’applique quand on part de l’ensemble des photons intiaux (++, –, +-, -+). Pourquoi la règle devrait s’appliquer aussi pour chacun des sous-groupes ? Cela ne me semble pas trivial.
Bonne journée.
Bonjour,
On suppose que les réglages de la machine qui émet les photons n’ont pas été modifiés entre les deux séries de mesures. Donc dans les deux cas les photons doivent avoir les mêmes variables cachées. Ou alors cela veut dire qu’en modifiant les polariseurs on affecte le processus qui émet des photons, ce qui rentre dans la catégorie des « spooky actions ».
J’espère que ça répond à ta question.
Bonne journée
Bonjour,
J’ai quelques remarques à faire sur les expériences de Bell-Aspect. Peut être que ce sera utile pour comprendre les choses.
Tout d’abord pour simplifier es choses, On a pas besoin de passer par les formules compliquées de Bell pour s’apercevoir que en MQ les 2 series de valeurs ou signaux physiques S1=S(teta1) et S2=S(teta2) en sortie de polariseurs sont liées et non indépendantes donc corrélées puisque la MQ prédit pour la corrélation de ces 2 séries une correlation du type cos(teta1-teta2) qui n’e sera jamais un produit du type S1*S2 , ce qui serait le cas si ces 2 séries étaient indépendantes.
Donc sans même parler des inégalités de Bell, on sait qu’on va avoir un problème.
Et remarquons aussi autre chose, vous avez vu que je parle de série de signaux S1 et S2 et non de mesures.
Rappelons ici la différence en MQ entre mesure et états ou fonction d’onde ou signaux comme je les appelle.
La MQ est très claire, il y a une grosse différence entre états et mesures. Je ne peux pas rentrer dans les détails mais en gros un état caractérise l’état d’une observation, c’est en général un vecteur à n composantes complexes (amplitude , phase) sans unité dans un espace de Hilbert alors qu’une mesure est un nombre réelle avec des unités (volt, mètre etc) qui est la valeur propre d’une matrice dites observable qui caractérise l’observation.
Concernant les expériences EPR la MQ prédit que la moyenne des mesures d’une observable dites de corrélation quantique correspond au produit scalaire des fonction d’onde et non à un produit simple des mesures. En MQ ces calcul de corrélations entre états sont présentés de la façon suivante =cos(teta1-teta2) qui est le produit scalaire de 2 états ou encore fonctions d’ondes ou encore signaux et non des mesures!
Si c’étaient des mesures on aurait E(s1*s2)=E(s1)*E(s2) qui correspond à la valeur moyenne de 2 séries indépendantes, ce n’est pas le cas!.
Je conclue donc que puisque les résultats obtenues dans les expériences de Bell Aspect sont conformes aux calculs de la MQ, les corrélations obtenues dans les expériences d’Aspect Bell ne sont pas des corrélations de mesures mais bien à des corrélations disons quantiques entre 2 vecteurs d’états quantiques préparés par 2 polariseurs distants.
Voilà, j’espère que je n’ai pas rajouté de la confusion à la confusion sur ce sujet.
Cdlt.
Je l’ai déjà dit, mais on ne m’écoute pas (lol) devant des résultats expérimentaux étranges comme ça, le travail du scientifique, son DEVOIR même, devrait être de découvrir la « combine », le truc qui nous échappe… En physique depuis une centaine d’année on a perdu ce réflexe d’essayer d’expliquer des phénomènes « étranges » rationnellement, et on admet n’importe quoi, l’inadmissible même, c’est plus de la science, on est revenu au temps des enchanteurs… On a peut-être « besoin » de ça, sans doute, de magie, dans notre vie si « normale »…
Et les pistes sont nombreuses à explorer pour découvrir « le truc » dans cette expérience… D’abord il me parait important de rappeler qu’un polariseur ne laisse pas « passer » ou pas une onde électromagnétique, il a seulement (et simplement d’ailleurs) pour effet de projeter l’amplitude de l’onde qu’il reçoit sur son axe, donc l’amplitude sortante dépend du cosinus de l’angle incident et notez que là il n’y a pas de puissance au carré, du coup ce n’est pas linéaire, ce qui expliquerait déjà les différences de soustraction entre les angles selon l’inclinaison à laquelle il sont fait si la réaction du détecteur dépendait de l’amplitude et non de l’intensité.
Ensuite il est très probable qu’il n’existe pas de telle chose, « un » photon, les ondes électromagnétiques sont (comme leur nom l’indique) de nature ondulatoire, la seule chose qui donne l’impression qu’elles sont corpusculaires c’est leur détection qui ne se déclenche qu’après un certain « seuil d’excitation » de la particule « surveillante » du détecteur, celle qui réagit et nous donne l’information.
Bref on a tous bien compris que c’était bizarre, c’est démontré même grâce à Mr Aspect. Alors : AU BOULOT ! Trouvons le « truc » !
Bonjour Fabien,
les inégalités de Bell ne font aucunement intervenir les concepts de photons ou de polariseurs. Comme l’explique David dans le texte qui suit la vidéo, il suffit de disposer de deux instruments de mesure distants, avec deux choix de mesure, ayant chacune deux possibilités. Si les résultats d’une expérience effectuée avec ces dispositifs viole les inégalités de Bell, alors on peut conclure que la théorie sous-jacente est nécessairement non-locale, sans même aller regarder de quoi sont faits les dispositifs de mesure. C’est ce qu’ont montré les expériences d’A. Aspect, et bien d’autres depuis.
Oui, c’est un résultat assez déconcertant, et les physiciens n’ont pas attendu vos recommandations pour essayer de trouver « le truc » : ils ont imaginé ces fameuses échappatoires, certaines vraiment farfelues, qui feraient que les conditions expérimentales ne vérifient pas les hypothèse du théorème de Bell. En vain !
Depuis un siècle, les physiciens explorent des domaines – l’infiniment grand, l’infiniment petit – qui échappent à la perception directe de nos sens. Il n’est donc pas vraiment étonnant qu’ils y trouvent des lois qui échappent à notre intuition directe. Mais alors ces lois sont cohérentes et rendent très bien compte des observations, devons-nous les rejeter sous prétexte que Fabien Sabinet ne les trouve pas « admissibles » ?
Ben si, l’expérience d’Aspect implique des photons et des polarisateurs… Et David prend l’exemple d’un dispositif « générique » qui violerait ces inégalités pour nous en faire comprendre le principe mais il n’existe pas… A part ces expériences à base de photons soit disant intriqués et de polarisateurs, il n’y a AUCUN autre dispositif expérimental qui violent clairement ces inégalités. Et heureusement.
Bien sûr que si. Ca a été fait avec des spins d’atomes, des jonctions Josephson, des ions piégés…
https://en.wikipedia.org/wiki/Bell_test_experiments#Notable_experiments
Si vous lisez les rapports d »expériences (et en particulier celle dont vous parlez sans doute de Hensen en 2015 qui recueille le meilleurs consensus https://arxiv.org/pdf/1508.05949.pdf) vous verrez que la détection des photons et l’usage de polariseurs est au coeur du dispositif expérimental (comme à chaque fois).
Ce que je veux dire, c’est que le fait que les expériences d’A. Aspect (et suivantes) violent les inégalités de Bell suffit pour conclure que la théorie qui décrit l’expérience est non-locale. Pour aboutir à cette conclusion, on regarde uniquement la statistique des événements en sortie de l’expérience, sans à aucun moment utiliser le fait que ces événements ont été obtenus en mesurant la polarisation de photons intriqués ou autres. Quand bien même des générations de physiciens se seraient fourvoyées avec le concept de photons, quand bien même on n’aurait pas compris le fonctionnement d’un polariseur, le résultat de non-localité resterait là, indépendamment de la modélisation de l’expérience. Il est donc vain de chercher un « truc » selon les pistes que vous avez proposées.
Là où la modélisation de l’expérience entre en jeu, c’est uniquement pour vérifier que les résultats sont en accord avec les prédictions de la mécanique quantique. Vous pouvez très bien arguer que la mécanique quantique n’est pas correcte, et proposer une autre théorie qui rendra compte de ces résultats, mais elle devra nécessairement être, elle aussi, non-locale.
Et puisque vous semblez y porter votre attention, il y a aussi des tests des inégalités de Bell avec des ondes électromagnétiques continues (https://arxiv.org/abs/1801.03194) pour lesquelles les détecteurs ne sont pas des compteurs de photons, et la polarisation n’est utilisée que pour multiplexer les signaux et non pas pour encoder l’état quantique.
Merci JL pour ce lien sur les ondes électromagnétiques continues, je vais étudier ça avec grand plaisir et grand intérêt.
Concernant, les expériences de Bell Aspect, on a une preuve de la non localité qu’à condition d’admettre qu’on effectue effectivement un calcul de corrélation sur les mesures faites au niveau des polariseurs mais est ce bien le cas? en réalité on fait un traitement analogique des signaux en provenance des polariseurs et donc c’est bien une corrélation quantique qui n’est pas du tout équivalente à une corrélation numérique sur les mesures. je ne suis pas non plus certain de l’interprétation qu’il faut donner au résultat quantique qu’on nomme abusivement corrélation, c’est en réalité la projection d’un état quantique sur un autre ou un produit scalaire dans un espace hilbertien des états . On est loin du sens classique de corrélation.
Salut,
Désolé de parasiter à nouveau ce blog pour de l’auto-promo, mais j’ai récemment fait une série de trois « vidéos » (plus des présentations sans son et pleines de texte que des vidéos…) sur la mécanique quantique qui peuvent peut-être trouver un intérêt chez ceux lisant ce billet : https://www.youtube.com/playlist?list=PL1m96–TUxs7ARukxILKrnNp9M1V1wUFH.
La deuxième évoque les inégalités de Bell et la troisième l’idée de Greenberger, Horne et Zeilinger (du Bell sans statistiques) mentionnée dans le billet.
Bonjour Marc, J’ai visionné vos vidéos intéressantes. Vos explications sur la nature complexe des matrices de transition est intéressante, je ne connaissais pas.
Mais je reviens sur la video EPR. je vous fais la copie du message mis sur youtube.
Les expériences imaginées par Bell sont effectivement celles des jumeaux par contre les expériences d’Aspect ne le sont pas. En réalité dans les expériences d’Aspect on a pas réellement les réponses des jumeaux sous forme de oui/non ou +/-1. C’est le collecteur de coïncidences qui donne les réponses oui/non +/-1. Avant c’est pas possible, la quantique est formelle sur ce point si on relève les réponses des jumeaux, on détruit la phase du signal et les coïncidences sont brouillées et alors les réponses relevées (les mesures) seront conformes aux inégalités de Bell. En quelque sorte c’est la MQ qui sauve la localité.
Vous êtes en train de dire qu’Aspect n’a pas testé EPR, que son expérience n’est qu’un simple interféromètre…
La phase est effectivement perdue là où les questions sont posées, mais c’est bien au niveau des polariseurs (éloignés l’un de l’autre) et non du collecteur de coïncidences (qui ne fait que… collecter les réponses).
À partir des polariseurs, les photons sont projetés dans un état de polarisation donné et y restent.
Ils étaient par contre en phase jusqu’à eux et le fait que les réponses des polariseurs coïncident malgré l’éloignement laisse bien penser que l’état quantique est délocalisé.
Je ne vois pas où j’ai pu dire que les expériences d’Aspect étaient simples, elles sont remarquables et ce ne sont pas des interféromètres de toute façon.
Si les phases sont brouillés au niveau des polariseurs, on ne peut pas avoir de corrélation quantiques conformes aux prédictions de la MQ, donc on est d’accord.
C’est comme l’expérience des fentes de young, si vous faites une mesure ou posez une question entre les 2 fentes sources et l’écran, vous détruisez la phase de l’onde et du coup les interférences. Si une question est posée entre la source et l’écran les corrélations quantiques sont aussitôt détruites.
J’imagine que Aspect a dû apporter le plus grand soin pour que les signaux électriques soient acheminés des photo multiplicateurs au corrélateur à l’abri de toutes questions perturbatrices de l’environnement avec un soin remarquable et beaucoup de talent de façon à préserver la phase des signaux au Maximum pour en final obtenir des réponses ou mesures propres et nettes au niveau du corrélateur sans quoi les réponses n’auraient pas été conformes aux prédictions de la MQ.
Désolé, je n’ai pas été clair. Je me doute bien que vous ne dénigrez pas l’exploit expérimental.
Par contre, si vous supposez que la mesure qui désintrique l’état quantique se fait au niveau du compteur de coïncidences (c’est ce que j’ai compris de votre commentaire, mais j’ai dû me tromper) alors ce n’est pas un test EPR.
La désintrication se fait dans les polariseurs (c’est le seul endroit où l’état quantique est mesuré) puisque l’expérience vise justement à questionner les photons lorsqu’ils sont loin l’un de l’autre, puis à regarder combien de fois ils sont d’accord entre eux. Il n’y a pas d’interférences dans le compteur de coïncidences, juste un signal lorsque les deux réponses sont les mêmes.
Une expérience plus ou moins équivalente avec les fentes d’Young s’arrêterait au niveau des fentes. La question deviendrait : les mesures du passage ou non dans chacune des fentes sont-elles corrélées même lorsque leur écart supposerait un signal plus rapide que la lumière de l’une à l’autre pour se mettre d’accord ? Il n’y aura bien sûr pas d’interférences derrière les fentes, mais ce n’est pas ce qu’on cherche ici à mesurer.
En d’autres mots : on regarde les corrélations entre les réponses classiques (non cohérentes) aux questions posées à un état quantique (cohérent).
Merci de bien clarifier où se situe le désaccord, au moins on est d’accord là dessus.
Vous pensez que les mesures sont faites au niveau des polariseurs mais pourtant vous parlez de signaux acheminés au compteur de coïncidence CC , si c’est un signal analogique alors il y a une phase et une amplitude, ce n’est pas une simple mesure +/-1. je pense que l’information de phase passe jusqu’au CC d’une manière ou d’une autre.
A mon avis , si on stockait les mesures +/-1 numérotées en fonction du temps sur 2 clés USB , une pour chaque polariseur , donc sans info de phase on est d’accord, et qu’on fasse ensuite un calcul numérique de corrélation sur ces valeurs numériques binaires alors on aurait sans problème des corrélations en accord avec les inégalités de Bell ou alors faudrait qu’on m’explique par où est passé l’info de phase.
A noter que la synchronisation des horloges distantes pour numéroter les 2 séries de mesure en fonction du temps poserait un sérieux problème.
Félicitation David,
Je connaissais l’expérience d’Alain Aspect pour avoir regardé ses vidéos sur le sujet. Mais je trouve que votre présentation est d’une grande clarté et quelle présente un aspect pédagogique remarquable. Je me permets de vous signaler une de mes élucubrations sur le sujet que vous trouverez dans mon blog cité ci-dessus. C’est beaucoup moins scientifique que vous mais la conclusion est un peu la même.
Au plaisir de vous suivre.
L’expérience d’Alain Aspect invalide l’hypothèse des variables cachées locales par violation des inégalités de Bell. Mais la théorie de la décoherence quantique ne serait-elle pas une « sorte » de théorie à variables cachées locales pour expliquer l’effondrement de la fonction d’onde?
C’est compliqué 🙂 Disons pour aller vite que la décohérence ne suffit pas pour expliquer l’effondrement de la fonction d’onde et de façon générale le problème de la mesure en mécanique quantique. Elle explique comment un état quantique peut interagir avec l’environnement (et s’intriquer), mais elle n’explique pas pourquoi à la fin on n’a qu’un résultat. Pour prendre des mots savants, dans la vision orthodoxe, le phénomène de réduction est un processus dit « non-unitaire » alors que la décohérence (et de façon générale tout ce qui suit l’évolution par l’équation de Schrödinger) est unitaire. Donc il reste un truc à expliquer
Un partisant de la théorie de la décoherence quantique pourrait dire que l’effondrement de la fonction d’onde n’est qu’une illusion, il n’y aurait pas qu’un résultat à la fin mais une fonction d’onde extrêmement concentrée autour d’un point, et négligeable ailleurs (mais non-nulle): une sorte d’unitarisation du processus d’effondrement de la fonction d’onde. L’interrogation sous-jacente à mon commentaire précédent est donc de savoir si l’expérience d’Alain Aspect invalide cette unitarisation parce qu’elle serait une théorie à variables cachées locales.
Bonjour David,
Je me demande si on peut on considérer que les phases et amplitudes des fonctions d’onde ou signaux en sortie des polariseurs ne sont pas justement ces variables cachées recherchées dans la mesure où ce sont justement ces info de phase et d’amplitude qui permettent de retrouver le bon résultat de corrélation quantique et ce en accord avec la localité.
Bonjour !
Il a quelque chose que je ne comprend pas !
Comment les 2 photons peuvent s’influencer instantanément à n’importe quel distance ?
Cela signifierai que les 2 photons communique plus vite que la vitesse de la lumière et donc cela contredirait la théorie de la relativité restreinte non ?
Merci d’avance pour ta réponse 😉
Eh bien oui il y a de ça ! Après dire que ça contredit la RR, c’est probablement aller un peu vite. Pour reprendre les termes techniques de Bell, c’est une violation de la causalité locale.
Je suis un peu perdu alors :p
Je pensais que rien ne pouvait se déplacer plus vite que la vitesse de la lumière et que c’était un des fondement de la RR.
Bonjour,
Il y a quelque chose que j’ai du mal à saisir sur la notion de photon intriqués. En effet, dans les expériences de Bell-Aspect, les photons intriqués ont des caractéristiques physiques (notamment la longueur d’onde) différente. La notion d’intriquation est-elle donc propre à une expérience? S’agit-il donc d’une dénomination empirique ou sommes-nous capable de prédire que deux photons seront intriqués?
Merci pour votre réponse et félicitations pour votre travail.
Oui la notion d’intrication peut être propre à une caractéristique (une « observable »), ici la polarisation
Bonjours. D’abord, je voudrais vous remercier pour vos vidéos. J’adore ces vidéos et j’ai appris beaucoup de choses en les regardant. Le français n’étant pas ma langue maternelle, j’ai parfois des difficultés à suivre certaines parties de vos vidéos. Des sous-titres en français donc seraient très appréciés. Encore une fois merci beaucoup!
Bonjour,
Peut-on affirmer que deux particules intriquées ne constituent pas en réalité le même « objet » ?
Autrement dit, deux particules intriquées ne pourraient-elles pas être la manifestation de la même chose ?
Merci pour ces vidéos passionnantes.
C’est une interpretation à laquelle je souscris. L’état intriqué est l’objet considéré, et il évolue dans l’espace de hilbert. Les clics des détecteurs ne sont que des valeurs propres des observables. Si ces clics sont localisés dans notre espace physique (et avons tendance à dire : quelque chose a provoqué cela), l’évolution du vecteur d’état est indépendante de l’espace physique. Il dépend du contexte expérimental.
Séparer les particules par la pensée, c’est apauvrir la réalité.
Bonjout David,
Merci pour cette super vidéo. Une question me taraude. Quand tu montres l’effet de l’orientation 2 polariseurs successif sur la transmission, ce que j’en comprends c’est que le 1er réduit le paquet d’onde dans le sens du 1er polariseur, et du coup le photon correspondant ne peut pas passer par un second polariseur à orienté à 90deg par exemple. On révèle l’état du photon, et sa probabilité de polarisation 90deg devient nulle. Mais si on intercale un 3eme polariseur entre les 2 premiers, et qu’on l’oriente à 45deg, on augmente la transmission. Donc la probabilité de passage du polariseur à 90deg n’est plus nulle. On re-introduit du « hasard » dans le comportement du photon, alors que le 1er polariseur était sensé avoir tué ce hasard. Pourquoi cet argument n’est pas un bon argument pour prouver le non-déterminisme ?
oui! alors cette expérience simple que tout le monde peut faire avec des verres polarisés de lunettes par exemple et une sources de lumière polarisée des diodes par ex. Voilà typiquement une expérience totalement incompréhensible, au même titre que les expériences de Bell, si on n’applique pas rigoureusement les principes de la MQ.
Voyons comment cette expérience se présente. On a une source S polarisée et 2 filtres Polariseurs P1 et P2 avec P1 intercalé entre S1 et P2 puis un écran de visualisation E ou l’oeil de l’observateur si on veut.
La chaîne de mesure se présente donc sous cette forme: S=>F1=>F2=>E.
La présence et la position de l’écran dans la chaîne de mesure est FONDAMENTAL. Faut bien comprendre où est faite la mesure. La MQ est très claire à ce sujet. La mesure est faite au niveau de l’écran pas avant. La réalisation de l’expérience , le comptage des photons se fait au niveau de l’écran pas avant. En MQ, l’existence du photon comme particule n’a pas de sens avant la réalisation de l’événement au niveau de l’écran . Entre la source S et l’écran E ,la MQ ne décrit l’expérience que sous forme d’état mais ne parle jamais de particule avant la mesure. D’ailleurs mettez un écran E entre P1 et P2 ou essayez de localiser les photons entre P1 et P2 et vous changez tout.
Moralité, l’endroit où est faite la mesure a toute son importance, la particule n’a pas de réalité physique avant la mesure sous peine de faire des erreurs , avant la mesure l’expérience et la réalité physique est décrite physiquement sous forme de vecteur d’état.
J’espère avoir apporté un peu plus de photons éclairants sur vos écrans dans la mesure de mes moyens.
Bonjour David
Comme toujours j’ai beaucoup apprécié votre vidéo ,même si je l’ai vue deux fois pour suivre…
J’aimerais beaucoup qu’un jour vous traitiez le réacteur au Thorium qui est décrit comme l’avenir énergétique de l’humanité, mais qui est très mal expliqué…
Bien a vous YC
Bonjour, je sais que je pose cette question un peu tard, mais j’espère qu’elle sera lue.
Je viens de voir une vidéo expliquant que la vitesse de la lumière n’a jamais réellement été mesurée, mais qu’on ne peut que mesurer un allé retour de la lumière. Ainsi la lumière pourrait se déplacer plus vite dans un sens de l’univers et moins vite dans l’autre, et toutes les prédictions de la relativité générale resteraient valides. Le fait que la lumière se déplace à la même vitesse dans toutes les directions de l’espace n’est qu’une convention (l’hypothèse de synchronisation de Einstein)
Pour l’expérience de Monsieur Aspect, la preuve de la non localité partait du principe que rien ne peut aller plus vite que c, or cette majoration pourrait être plus haute si la lumière se déplaçait plus rapidement dans un sens de l’espace.
N’est pas là une faille restante de la localité ?
L’homogénéité et l’isotropie de l’espace sont à la base de la relativité restreinte. L’arrivée et le départ n’ont pas de signification spécifique pour la physique.
N’ajoutons pas des hypothèses farfulues pour compliquer la simplicité qui est là.
La localité revient à dire que l’influence à distance instantanée d’un événement sur un autre est impossible. La localité est à la base de la relativité. Pas de localité, pas de relativité. Si je comprends bien , si les expériences de Bell Aspect remettent en cause la localité, alors il faudrait rejeter la relativité, mais pas seulement, il faut rejeter toute la cosmologie actuelle, les modèles de Friedmann Lemaître, le Big-Bang, mais pas seulement une bonne partie de la physique nucléaire, les anti particules n’ont plus de sens , la théorie Quantique des champs, voir même les équations de Maxwell bref il faut poubeller le travail de centaines de milliers de chercheurs du XXe et XIXe siècle etc etc…et sans localité il faut aussi remettre en cause la causalité, alors là ça va plus loin c’est le travail des scientifiques depuis des millénaires… et même on se demande si la sciences est possible car si il n’ y a pas de causalité, il n’ y a plus d’explications rationnelle , c’est presque remettre en cause la raison.
Une telle remise en question n’est-elle pas en effet diablement insupportable ? (A moins qu’elle soit excitante ?)
L’expérience EPR nous montre que le clic d’un détecteur n’est pas causé par un objet localisé sur le détecteur. C’est choquant pour notre cerveau mais c’est bien le résultat de la MQ.
Je vous renvoie aux conférences d’Etienne Klein sur le sujet (celle ci par exemple : https://youtu.be/8vNtPd_4E74) qui sont très bien vulgérisées.
Je crois qu’on a pas la choix, Si 99,9999% de la physique nous dit qu’elle est locale alors si on voit un physicien qui nous dit qu’il a un résultat expérimental qui montre le contraire , c’est qu’il y a sûrement un problème dans l’interprétation de l’expérience et des résultats, faudrait plutôt chercher l’erreur tout simplement.
Les pistes pour chercher, je les ai déjà exposées plus haut. AMHA, le problème d’interprétation majeure est qu’ il n’ y a pas de mesures au niveau des polariseurs même si ils émettent des « clics » , la mesure quantique est faites au niveau du CC localement , avant la mesure ce sont des états ou signaux qui ont aussi une réalité physique et décrivent parfaitement l’expérience en accord avec la localité donc avec 99,9999% de la physique. merci!
Je connais par coeur les vidéos de Klein, elles sont excellentes, c’est grâce à lui que j’ai repris goût à toutes ces questions de physique. Pour moi la question EPR est résolue, je suis passé à autre chose.
Nous savons bien que la relativité générale et la théorie quantique des champs ne sont pas compatibles. Cela n’a conduit personne à « rejeter » entièrement l’une ou l’autre. Simplement, nous imaginons qu’il doit y avoir des circonstances dans lesquelles l’une ou l’autre (au moins) est prise en défaut, et qu’il faudrait peut-être les déduire comme des limites d’une théorie plus fondamentale. Bref, il se pourrait que nous ayons à « rejeter » la relativité, mais seulement dans le même sens où la relativité elle-même à conduit à « rejeter » la mécanique newtonienne ou la théorie de l’électromagnétisme de Maxwell (ce qui ne revient pas du tout à tout jeter à la poubelle, me semble-t-il). Le fait que tout ne soit pas soumis au principe de causalité locale ne signifie pas que rien ne le soit : cela pose simplement une question : à quelles conditions un phénomène physique l’est-il?
Bonjour David,
Merci pour cette vidéo passionnante qui m’a permis (enfin!) de bien comprendre les inégalités de Bell ainsi que l’expérience d’Alain Aspect. Question: tu affirmes que la préoccupation principale d’Einstein n’était pas le déterminisme, mais la non-localité. Sur quoi bases-tu cette affirmation? Il me semble en effet qu’à la question: « que feriez-vous si il apparaissait que la physique ne répondait pas à la loi de la causalité », Einstein aurait répondu: « alors je me désintéresserais totalement de la physique » (les citations sont très approximatives, je m’en excuse).
Deuxième point, j’attends avec impatience la présentation sur de Broglie – Bohm. Comme tu le sais, lors du congrès Solvay de 1927, de Broglie avait « rejoint le camp » de l’interprétation de Copenhague. Mais il s’en est mordu les doigts – il a affirmé plus tard que c’était l’erreur qu’il regrettait le plus. Après guerre, il a rejoint Einstein et le « clan » des déterministes. C’est cette position qui fait qu’il a été depuis lors ostracisé par la communauté scientifique française, et que tous ses travaux ont été délibérément ignoré par cette communauté: en particulier sa théorie des particules à spin, qui offre un vaste sujet de réflexion et d’études dans bien des domaines. On peut citer ses travaux avec Marie-Antoinette Tonnelat, qui sont les seuls, à ma connaissance, à avoir apporté des résultats sur la synthèse entre mécanique quantique et relativité générale.
Bref, un article sur de Broglie-Bohm remettrait un coup de projecteur sur ses travaux, et montrerait à tous les jeunes physiciens qui te lisent qu’il y a une vie en dehors de l’interprétation de Copenhague! 😊
Bonjour David,
Merci beaucoup pour ta vidéo. J’ai une question.
Je cite «Pour avoir le bon état superposé, il faut s’imaginer que c’est une source de photons uniques polarisés circulairement ». A t-on une superposition de la polarisation circulaire droite et de la polarisation circulaire gauche quand les photons uniques sortent du dispositif ? Pouvons-nous également imaginer cette superposition dans une autre base (base horizontale/verticale ou base diagonal/antidiagonal) ?
En fait une polarisation circulaire (gauche ou droite) va correspondre à un état superposé dans n’importe quel choix de base linéaire
Merci pour la vidéo. super intéressant.
Trois questions d’un non-initié:
– Pouvez vous partager toutes les valeurs (percentages) du tableau?
– D’un point de vue de vulgarisation, peut-on imaginer l’experience suivante: On a une barre de fer d’une longueur de 10^6 km. Si je tourne la barre de fer d »une extrémité, alors la question est: est-ce que l’autre extrémité de la barre de fer tournera de façon instantanée? ou alors il y aussi la contrainte de la vitesse de la lumière?
– Souvent, en face d’incohérence de ce type (when we hit a wall) la solution est d’imaginer une dimension supplémentaire. C’est le cas du nombre imaginaire pour les nombre complexe ou encore la variable latente (cachée) dans le paradoxe de simpson (statistique). Pour la violation de l’inégalité de bell, un bon nombre de commentaires ont suggéré la dimension supplémentaire, et vous avez cité conjecture dite « EPR=ER ». Alors pour accepter une variable caché (dimension supplémentaire), il faudra que la localité ne soit pas respectée. En d’autres termes, la fonction de la variable cachée est justement d’expliquer la non-localité, par une localité dans une dimension supplémentaire. Ma question est, dans cette conjoncture EPR=ER, est-ce que la théorie de la relativité est respectée (y compris la limite de la vitesse par la vitesse de la lumière)? si oui, peut-on dire que la localité est respectée non pas dans cet espace+temps mais dans l’expace+temsp+la_dimension_supplémentaire. est-ce un raisonnement qui tient la route?
Merci pour toutes vos vidéos
Désolé, j’ai écris mon commentaire avant de finir la video. Je viens de continuer la vidéo, donc il y a bien une explication avec une variable cachée non-locale Broglie-Bohm.
Vivement une vidéo sur ce sujet
Bonjour,
J’ai une question mais je ne sais pas faire les calculs nécessaires pour y répondre (mes bidouillages donnent n’importe quoi). Si on prend un triplet de photons intriqués, ça doit bien donner une distribution de probabilité sur toutes les possibilités du style « passe à 0°, passe à 22.5°, ne passe pas à 45° », n’est-ce pas ? Quelle est cette distribution de probabilité et quel est son lien avec les distributions de probabilités pour les couples d’orientations ?
Eh bien on peut « en principe » imaginer trois photons intriqués avec n’importe quelle superposition de résultats sur un choix de base d’orientation donnée. Donc par exemple décomposer sur la base (+++;++-;+-+;-++;etc. il y 8 cas possibles)
Bonjour,
Merci pour votre réponse. Cependant j’aurais voulu savoir quelles sont les probabilités de ces 8 possibilités.
Si j’ai bien compris, le résultat se reformule comme suit. Pour chaque paire de filtres parmi 0°, 22.5°, 45°, la mécanique quantique prédit une loi de probabilité sur l’espace des couples de {passe,ne passe pas}. Le résultat est qu’il ne peut pas y avoir de loi de probabilité sur les triplets de {passe,ne passe pas} de sorte à induire les probabilités prédites sur les espaces associés aux couples de filtres. Pourtant, si on fait l’expérience avec trois photons intriqués, on devrait avoir une loi de probabilité sur ces triplets de {passe,ne passe pas} ! Le fait qu’elle n’induise pas les bonnes probabilités sur les espaces de couples veut dire que les résultats de l’expérience avec trois photons intriqués sont différents suivant si on oublie l’un des photons ou si on le prend en compte ?
Il doit donc y avoir une frontière entre « prendre le troisième photon en compte » et « ne pas le prendre en compte ». Pourtant, il y a un continuum entre ces deux alternatives, je ne vois pas comment on pourrait ne serais-ce que définir une séparation entre les deux. Alors comment est-ce que la mécanique quantique résout ce paradoxe ? Je veux bien accepter que la mécanique quantique soit un modèle totalement contre-intuitif du monde, mais que répond-il à ce que je viens de dire ?
Non en fait c’est plus compliqué que ça.
L’état (intriqué) est défini par la donnée des coefficients complexes sur chacun des 8 vecteurs de base, appelons les a,b,c,d,e,f,g,h. (en fait seulement 7 car la somme des modules carrés doit faire 1).
Une fois qu’on a fixé l’état en choisissant ces coefficients, on se choisit 3 angles pour régler nos polariseurs, et dans ce cas il existe (pour cet état là et pour ces angles là) une distribution de probabilité des résultats sur les 8 possibilités. Cette distribution va dépendre des 8 (7) coefficients et des 3 angles.
En théorie on peut la calculer, en pratique ça va prendre un peu de place 🙂
Bonjour,
Merci de vos réponses.
C’est normal que mes autres commentaires ne soient pas apparus ? Je réitère.
Je disais juste que du coup j’avais posé la question sur physics.stackexchange et en fait les calculs naïfs que j’avais fait étaient les bons. Le truc qui est étrange, c’est que dans le cas de deux photons intriqués, il y a une symétrie de rotation : quand on tourne chaque filtre du même angle, rien ne change. Mais quand on ajoute un photon de plus, ce n’est plus le cas ! C’est pour ça que je croyais que ce n’était pas correct.
J’ai aussi appris l’existence de cette expérience qui utilise trois photons intriqués : https://en.wikipedia.org/wiki/GHZ_experiment
Enfin, je ne comprends toujours pas comment c’est possible que le résultat d’une expérience dépende de quelque chose qui n’est pas pris en compte dans l’expérience (le troisième photon). Apparemment, il n’est pas possible de juste « oublier » le troisième photon d’un triplet intriqué pour obtenir un couple de photons intriqués.
Ah oui mince, c’est tombé dans les commentaires à modérer !
questions de noob (j’espère que le vocabulaire que je façonne est compréhensible):
1) (10’28) c’est un photon-onde qui devient photon-corpuscule au « proba-contact » de l’écran (il me semble). Du coup je vois pas trop ou la localité est bousillé : « la fonction d’onde change partout pour être 0 partout sauf au point d’impact »
wiki : principe de localité est un principe selon lequel des objets distants ne peuvent avoir une influence directe l’un sur l’autre
quand bien même mon photon-onde compterait pour un objet, je suis pas sur qu’on puisse parler de « distance » vu que il a pas une réel coordonnée mais un ensemble de proba-coordonné. En gros, ça me donne l’impression que ça dépend de mon interprétation (contrairement a une balle de tennis qui serait voyage plus vite que la vitesse de la lumière) . Non? (de plus je voudrais savoir si l’ensemble des proba-coordonné du photon est un nuage ou un disque parrallele à l’écran)
2)13’38 : on fait une superposition des 4 situations (++ +- -+ –)d’après la physique quantique. Pourquoi on fait pas un ensemble de 2 superpositions (Photon gauche, Photon droite) des 2 situation (+ ou -)? Alors oui dans la finalité les 4 situations existent. Mais ça change/lie/symetrise les possibilité possible non? Disons filtre gauche filtre Pg (en % =>E[0;1]) et filtre droite filtre Pd(en %).
En faisant mon arbre de proba, j’ai 4 équations avec 2 inconnus :
– – : Xg*Xd (exemple video 32% et 50%)
– +: Xg*(1-Xd) (exemple video 5% et 0%)
+ – : (1-Xg)*Xd (exemple video 46% et 0%)
++ : (1-Xg)(1-Xg) (exemple video 17% et 50%)
du coup si je « decide » de me mettre dans un systeme — 50% et ++ 50%,
mes proba + – et ++ ne sont pas illimité en choix (et d’ailleurs l’exemple vidéo me semble impossible pour moi).
Enfin bref je comprend pas et vu que je suppose qu’on arrive bien a faire votre exemple 50% ++ et – -, je vois pas trop en quoi mon raisonnement est faux (ou alors je sais pas, faut faire des proba avec des nombres irréel?)
1) C’est pour ça que je précise que c’est un argument illustratif uniquement utilisé de façon initiale par Einstein, pas un truc super carré.
2) Eh bien justement si on fait un ensemble de deux superpositions, on a un état non-intriqué, ce qui est un sous-ensemble des états possibles (ceux qui se factorisent). Mais les états non-intriqués n’épuisent pas toutes les possibilités.
Vous êtes presque plus rapide que la vitesse de la lumière pour me répondre. Merci^^
J’ai bien aimé cette vidéo. Claire et agréable à suivre. J’ai écrit il y a longtemps une petite nouvelle de SF qui s’inspire de la corrélations des particules, en détaillant un peu la violation des inégalités Bell. Mais je me pose une question. dans l’expérience de A. Aspect, les polariseurs sont à égale distance de la source (6 mètres il me semble). Imaginons que l’on place un polariseur à 6 m et l’autre à 12 m. Je pense que cela ne devrait rein changer puisque les photons sont intriqués, non ?
Don si la source n’envoie pas de particule intriquer mais des particule déterminer a l’avance, combien y a il de Sigma?
Quelqu’un a fais l’expérience?
Donc si la source n’envoie pas des particules intriquer mais des particule déterminer a l’avance, combien y a il de Sigma?
Quelqu’un a fais l’expérience?
N’y a-t-il pas un autre échappatoire?
Si c’est un générateur quantique qui commande la position aléatoire des polarisateurs, ne peut-on pas penser que la raison (quantique, inconnue) qui fait décider d’une position du polarisateur… fasse AUSSI décider de la polarisation des particules? Et créer un biais systématique.
C’est comme si je demandais à un hacker de choisir le mot de passe de ma carte de banque!
Il faudrait refaire l’expérience en choisissant autre chose comme générateur aléatoire. Comme les décimales d’un nombre transcendant (?) Il faudrait que le photon soit balaise pour les deviner!
Bonjour,
Merci beaucoup pour votre superbe travail !
J’essaie très fort de comprendre mais j’ai beaucoup de mal à accepter la non-localité (je serais plutôt partisan de laisser tomber le principe de causalité pour pouvoir conserver une forme de localité).
J’essaie de comprendre ce qui se passerai si on faisait l’expérience avec 3 photons intriqués, et 3 détecteurs, mais je tombe sur un os : si on envoie seulement les résultats de 2 des détecteurs à un scientifique, il devrait retrouver les statistiques et les corrélations présentées ici sans pouvoir se douter qu’il y avait un 3ème détecteur non ? En partant de cette hypothèse, j’essaie de calculer à quoi peuvent ressembler les résultats globaux mais je trouve des probabilités négatives pour certaines configurations !
Il doit y avoir quelque chose que je n’ai pas encore compris dans ces expériences …
superbe et limpide exposé, merci David !
Une question, si demain matin je rencontre un photon, y-a-t-il un moyen de savoir s’il est intriqué avec un autre photon (éventullement hors de portée) ou pas ?
Eh bien non, c’est bien le problème 🙂
Pour savoir des choses sur un système quantique, on doit « mesurer », et quand on fait ça on ne reçoit qu’une réponse unique, mais pas d’information sur l’état quantique en général. Si on n’a qu’un seul exemplaire du système en question, aucun moyen de savoir s’il est dans un état « propre », dans une superposition, intriqué ou pas, …
Merci pour la réponse superluminique !
Une autre question David. Supposons qu’une expérience ait fourni le résultat suivant : un photon A (non polarisé) est passé avec succès au travers un polariseur P. Imaginons maintenant qu’avec ce même photon A, au lieu de cette expérience là, nous en ayons conduit une autre avec pour seule différence que le polariseur est décalé d’un mètre. Que dit la théorie quantique, le photon serait-il passé au travers ou au contraire les deux possibilités passage-bloquage auraient été équiprobables ?
Si le photon est passé à travers un polariseur, c’est équivalent à une mesure donc il sera polarisé dans cette direction. Elle na varira pas avec la distanc ensuite.
ce n’est pas la question. La question est « Imaginons maintenant qu’avec ce même photon A, au lieu de cette expérience là,… »
J’avais effectivement mal compris la question. La probabilité que le photon passe ne change pas avec la distance. Le vecteur d’atat n’évolue pas car rien n’influence le comportement du photon. Seul le polariseur « fait la mesure. »
Il faut raisonner avec un grand nombre de photons ou la probabilité de passer le polariseur.
(on ne peut pas dire, ce photon là, spécifiquement, que se serait il passé si …) Tous les photons de l’univers sont identiques. On est obligé de faire l’expérience plusieurs fois pour obtenir la probabilité.
la question n’est pas :
« que se serait il passé si… »
mais :
« que répond la théorie quantique, A ou B ? » (cf. A et B ci-dessous)
Si elle répond A, elle dit « le photon serait passé avec certitude », mais si elle répond B, elle ne fait que dire que les possibilités sont équiprobables, sans dire ce qui se serait passé.
Quelqu’un saurait-il dire si c’est A ou B ? @David ?
Encore faut il que la question soit bien posée…
Modifier une expérience dans sa tête qui a déjà été réalisée et se demander quelles aurait été le résultats n’a aucune utilité pratique. Une expérience, un résultat.
Désolé d’être un peu brute, je ne peux pas aider plus.
oui, c’est vrai, le résultat n’a aucune utilité pratique (mais ceci est une autre question, on a bien le droit intellectuellement de se poser des questions sans utilité pratique), et je me demande si la conclusion n’est pas « aucune théorie scientifique ne peut répondre à cette question puisqu’elle n’est pas réfutable » (cf. https://fr.wikipedia.org/wiki/R%C3%A9futabilit%C3%A9 ). Bon, je reste un peu sur ma faim, merci quand même Pierre.
ce n’est pas encore tout à fait la question, il faut répondre A ou B :
A : le photon serait passé au travers,
B : les deux possibilités passage-bloquage auraient été équiprobables.
(il sagit d’un expérience invérifiable expérimentalement puisque par hupothèse l’expérience a déjà été menée et on ne peut pas la refaire avec le même photon. C’est une question purement théorique portant sur la théorie quantique)
Bonjour, j’ai je crois assez bien compris l’article (en même temps je suis en train de suivre un cours d’introduction à la mécanique quantique) et ça m’a enlevé deux ou trois idées fausses que j’avais en tête. Je reste un peu sur ma faim avec la fin de la démonstration de l’inégalité de Bell (le moyen ou il faut montrer que =∫Λ𝑑𝜆𝜌(𝜆)[(0,𝜆)(0,𝜆)+(1,𝜆)(0,𝜆)+(0,𝜆)(1,𝜆)–(1,𝜆)(1,𝜆)] < 2 ). Est-ce que tu aurais une bonne source ou je pourrais trouver la fin de cette démonstration, ou alors des indices comment y arriver par moi-même?
Dans tous les cas merci pour tout ce que tu fais, ça fait environ 6 ans que je te suis (depuis mes quinze ans) et maintenant je me retrouve à étudier la physique au niveau universitaire, et tes vidéos me plaisent toujours autant.
C’est comme en programmation ? Quand une variable n’est pas locale, elle est globale ?
Bonjour,
Question certainement naïve, mais pourquoi l’influence instantanée à distance, ne s’explique pas par la relativité des distances (et durées) selon la théorie d’Einstein?
Dans le référentiel de l’observateur on a bien une distance mesurée d entre les photons
Mais dans le référentiel des photons d’=d/γ avec γ => ∞ (transformation de Lorentz avec différence de vitesse => c vitesse de la lumière)
donc d’ => 0
Dans le référentiel des photons, ils ne sont pas à distance, mais au même endroit
Les mesures de corrélation sont faites par l’expérimentateur avec les moyens de son labo donc dans le repère de son labo. Autrement dit, le physicien qui fait la mesure ne voyage pas à la vitesse de la lumière, il fait les mesures de corrélation localement dans un repère lié à son labo.
Pingback: A la recherche du réel - BLOmiG - Bernard d'Espagnat
Et un prix Nobel pour Alain Aspect (entre autres !), un 🙂
bonjour , tous d’abord bravo pour vos videos de vulgarisation
je voudrais savoir si alain aspect a fait un livre sur ces experiences ? peut importe le niveau
cordialement
jerome
Il y a des conférences de lui sur ces sujets sur youtube. J’avais également trouvé un article de la démonstration simple des inégalités de bell sur google.
Bonjour,
Ma question va certainement paraître naïve mais il y a un point qui me gêne dans cette histoire, dès le début de la démonstration à laquelle je m’intéresse depuis l’attribution du prix Nobel à Alain Aspect. Pourquoi les photons intrigués, puisqu’ils ont même polarisation (ou des spins inversés s’il s’agit d’électrons) conduisent à des possibilités de corrélations lorsqu’il y a un angle non nul entre les détecteurs? Aucune coïncidence ne devrait intervenir dans un raisonnement « classique ». Comment explique-y-on qu’il puisse y avoir 2 détections positives alors que les 2 détecteurs ne sont pas alignés mais font un angle entre eux? Merci d’avance et bravo pour les vidéos, même si elles ne m’ont pas permis de tout comprendre !
Bonjour David,
Je commente un peu tardivement cette vidéo car je suis tombé un peu tard dans le « rabbit hole » de la physique quantique!
Dans la vidéo vous dites qu’on ne peut pas mettre à profit la propriété de l’intrication pour communiquer de manière supralumique car il n’est pas possible de forcer le résultat d’une mesure, qui sera toujours aléatoire.
Et si toutefois on considère le fait d’avoir fait une mesure, et donc le fait de ne plus avoir d’état superposé comme un bit d’information (0 ou 1), pourquoi cela ne marcherait il pas?
Merci beaucoup!
Bonjour David, j’ai une question. Pourrait-on imaginer que 1) la variable cachée se trouve dans l’environnement, sa valeur déterminant le résultat de la mesure via le processus de décohérence, et 2) que cette variable cachée se propage à la vitesse de la lumière, ce qui lui permettrait d’affecter les mesures sur chacun des photons sans qu’il y ait besoin d’invoquer une non-localité ?
Bonjour j’ai une question,
Dans l’expérience d’Alain Aspect on dit que les paires de photons intriqués produits par la source sont espacés de 2 ns.
Question 1 : comment des photons peuvent ils être intriqués avec ce décalage ?
Question 2 : comment peuvent-ils par la suite se comporter de la même façon au même moment lors de la mesure ou alors ces 2 ns sont elles toujours là ?