La vidéo du jour parle d’un sujet que j’avais brièvement évoqué dans mon épisode sur la relativité restreinte, mais qui méritait bien un traitement spécifique : le paradoxe des jumeaux de Langevin.
Et si les jumeaux communiquent ?
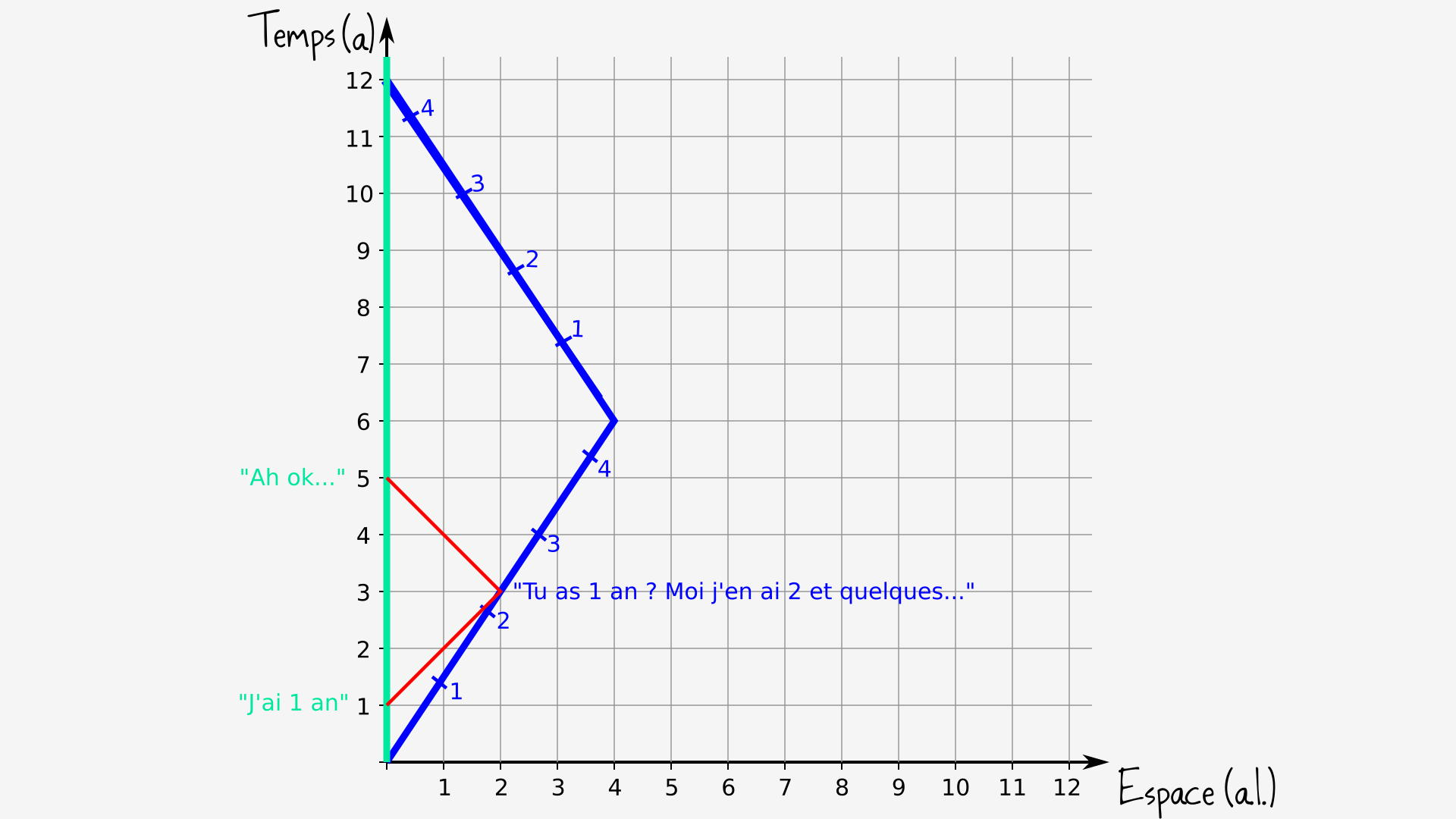
(Edit 08/03/20) Je n’avais pas anticipé que tant de gens poseraient la question de ce qu’il se passe si les deux jumeaux communiquent « par téléphone » (ou autre) pour comparer leurs âges en permanence.
Eh bien ça ne marche pas de façon si simple, car la communication ne peut pas aller plus vite que la lumière ! Voici un schéma qui montre à quoi pourrait ressembler la conversation. Au bout d’un an dans son référentiel, le jumeau terrestre envoie un message pour donner son âge (1 an donc). L’autre le reçoit au bout de 2 ans et quelques (dans son référentiel), et décide de répondre. Le jumeau terrestre n’aura la réponse qu’à 5 ans (dans son référentiel).
Temps propre et temps des coordonnées
Il y a un point essentiel à bien comprendre pour saisir toute la saveur du paradoxe des jumeaux, et j’espère avoir réussi à le faire passer dans la vidéo : la différence entre la notion de temps propre, et celle de « temps des coordonnées ».
Prenons deux événements E1 et E2 de l’espace-temps. On peut choisir un référentiel inertiel, et exprimer les coordonnées de ces deux évènements dans ce référentiel : \((x_1,t_1)\) et \((x_2,t_2)\). On peut alors calculer l’écart de temps
\(\Delta t = t_2 – t_1\),
entre ces deux événements, écart mesuré dans le référentiel qu’on a choisit. Comme je l’explique dans la vidéo, cet écart dépend du référentiel et dans un référentiel différent, les évènements auront d’autres coordonnées et on obtiendra une autre valeur \(\Delta t^\prime\).
Le temps propre (souvent noté \(\tau\)) est, lui, une grandeur associée à une trajectoire, pas juste aux 2 événements qui se trouvent aux extrémités. En revanche, et c’est important, cette grandeur est absolue, indépendante du référentiel. Pour le voir, regardons dans le détail comment on calcule ce temps propre.
Prenons deux événements, et une trajectoire qui les relie. Pour commencer simple, imaginons une trajectoire rectiligne uniforme. Plaçons nous dans le référentiel inertiel qui coïncide avec cette trajectoire. Dans ce cas, le temps propre est égal à l’écart de temps des coordonnées \(\Delta t\) mesuré dans ce référentiel. Mais attention, ça n’est pas comme ça qu’il faut se le représenter ! Il faut plutôt le voir comme la distance d’espace-temps \(\Delta s\) qui sépare ces deux événements.
La distance d’espace-temps entre deux évènements se définit comme
\(\Delta s = \sqrt{(c \Delta t)^2 – (\Delta x)^2}\)
Evidemment, dans le référentiel qu’on vient de choisir, les deux évènements se produisent au même endroit, donc \(\Delta x=0\) et \(\Delta s = \Delta t\). Mais définir le temps propre comme \(\Delta s\) est plus générique, puisque cette définition marche dans n’importe quel référentiel et fourni une quantité absolue : je le rappelle, la distance d’espace-temps est la même dans tous les référentiels.
Là on l’a fait pour une trajectoire rectiligne uniforme. Maintenant imaginez une trajectoire quelconque. Pour faire simple on va se la représenter comme une succession de petites trajectoire rectilignes uniformes. Dans ce cas là on peut calculer la distance d’espace-temps \(ds\) sur chacun de ces petits bouts de trajectoire, et additionner le tout.
Mathématiquement, on peut définir le temps propre entre deux événements le long d’une trajectoire T quelconque comme l’intégrale de la distance d’espace-temps
\(\displaystyle \tau = \int_T ds\).
Et là on a bien une grandeur invariante, absolue, qu’on peut calculer dans n’importe quel référentiel : le temps propre est la longueur d’espace-temps de la trajectoire.
Maintenant un point important à préciser : derrière l’idée du paradoxe des jumeaux, il y a une hypothèse sous-entendue, qui n’est pas forcément apparente, qu’on appelle l’hypothèse de l’horloge. Cette hypothèse dit que le temps mesuré le long d’une trajectoire par une horloge physique (quel que soit son mécanisme, supposé sans défauts) est justement le temps propre de cette trajectoire. Les horloges physiques mesurent le temps propre.
On peut trouver cette hypothèse « évidente » … ou pas ! Mais elle fait partie des « axiomes » de la relativité restreinte. Et le test de Hafele et Keating (et les autres depuis) ont justement permis d’aller dans le sens de cette hypothèse.
(Cette hypothèse est très bien mise en avant et discutée dans l’article de Pierre Spagnou dont je parle un peu plus bas.)
Distance d’espace-temps et contraction des longueurs
Dans cet épisode, je me suis concentré sur les effets temporels, et donc je n’ai évoqué que la « dilatation du temps », mais pas son phénomène symétrique : la « contraction des longueurs ».
Et pour une interprétation complète, il faut y faire référence quand on regarde les détails. Prenons les muons cosmiques. Vus de la Terre, les muons « vivent » environ 20 microsecondes…et comme on les voit se déplacer à une vitesse proche de celle de la lumière, on les voit parcourir environ 6 kilomètres.
Mais le muon, lui, ne vit que 2 microsecondes dans son propre référentiel. Il verra donc la surface de la Terre se rapprocher de seulement 600 mètres.
6 kilomètres vs 600 mètres : la distance entre deux évènements est relative.
Il se passe la même chose avec nos jumeaux. Celui de la Terre voit l’autre aller aux 2/3 de la vitesse de la lumière, et considère que la distance Terre-Proxima est de 4 années-lumière : il en déduit donc que le temps de parcours de son frangin sera de 6 ans.
Celui de la fusée se considère immobile (dans son propre référentiel) et voit Proxima se rapprocher de lui aux 2/3 de la vitesse de la lumière. Mais à quelle distance voit-il Proxima au début ? Puisque le voyage ne va durer que 4 ans 1/2, cela ne peut pas être 4 années-lumières. Cela sera seulement environ 3 années-lumière.
La distance Terre-Proxima n’est pas la même suivant le référentiel. Du fait de son mouvement, celui de la fusée « voit » cette distance plus courte que son frère terrestre.
Si tout cela vous semble confusant : une chouette référence c’est la série de MinutePhysics où il joue avec un objet qu’il s’appelle le « globe d’espace-temps », qui permet de visualiser les changements de référentiels. Une belle invention !
L’accélération
Parlons un peu de l’accélération. C’est souvent source de confusion, car on lit parfois que la relativité restreinte ne traite pas des corps en accélération. C’est évidemment faux ! On peut très bien traiter l’accélération, et il y a l’équivalent de la loi de Newton, mais qu’on écrit avec des « quadrivecteurs » :
\(F^{\mu} = m A^{\mu}\)
C’est d’ailleurs un exercice classique de relativité restreinte que de traiter le cas d’un objet uniformément accéléré.
Comme je le disais plus haut, dans le cas générique d’une trajectoire accélérée, on peut calculer le temps propre en faisant une intégrale qui considère en chaque point le référentiel inertiel localement coïncident.
Je le discute dans la vidéo, on peut se demander si c’est l’accélération en elle-même qui provoque la différence entre les deux jumeaux ? Comme je l’ai dit, stricto sensu c’est plutôt le caractère non-inertiel de la trajectoire qui induit la différence. Mais évidemment le caractère non-inertiel est ici une conséquence directe de l’existence d’une accélération.
Prenons une analogie : sur un terrain plat, la trajectoire en ligne droite est la plus courte. Une trajectoire qui ne va pas tout droit sera plus longue. Une telle trajectoire comprend nécessairement « des virages ».
Est-ce qu’on peut dire que ce sont « les virages » qui rallongent la trajectoire ? Pas vraiment, mais le caractère « non-direct » de la trajectoire est concomitant avec l’existence de virages.
Bref, savoir si c’est vraiment « l’accélération » qui crée la différence n’a pas vraiment de sens. Surtout que comme je l’ai dit, la différence n’existe de façon absolue qu’une fois les jumeaux réunis.
Il existe une variante de l’expérience qui prétend démontrer que l’accélération n’a pas de rôle, et qui se fait avec 3 jumeaux portant des horloges (un qui reste sur Terre, un qui part, et un qui part de Proxima). Quand les deux jumeaux voyageurs se croise, celui parti de la Terre communique à l’autre la valeur de son horloge. Pas d’accélération, mais je n’aime pas trop cette façon de faire car dans cet expérience, on perd la notion d’une même horloge physique faisant toute la trajectoire.
Une autre expérience amusante consiste à prendre des univers ayant des topologies non-triviales (disons un tore) et donc le fait que le jumeau de la fusée puisse revenir au point de départ et retrouver son frère sans avoir jamais du faire demi-tour ! Dans ce cas, il faut réfléchir à la notion de référentiel inertiel dans un espace de ce genre.
J’en retoucherai un mot plus tard. Pour les curieux :
Barrow, J. D., & Levin, J. (2001). Twin paradox in compact spaces. Physical Review A, 63(4), 044104.
Uzan, J. P., Luminet, J. P., Lehoucq, R., & Peter, P. (2002). The twin paradox and space topology. European journal of physics, 23(3), 277.
L’expérience de Hafele-Keating
Je dois vous avouer une chose : quand j’ai appris la relativité restreinte (en master à l’époque), je ne m’étais pas du tout intéressé à l’expérience de Hafele-Keating. Je ne suis même pas sûr qu’elle ait été mentionnée dans mon cours, ou peut-être qu’elle l’a été et que je n’y ai pas prêté attention.
Dans ma tête, on avait testé le paradoxe avec des horloges atomiques, mais je n’avais jamais retenu les détails.
Or un article très intéressant sur le sujet est celui de Pierre Spagnou : l’expérience cruciale de Hafele et Keating. Il m’a appris plusieurs choses sur cette expérience.
Cet article met très bien en lumière l’importance de l’expérience. On y trouve l’expression de la valeur du décalage (relatif) d’une horloge qui voyage :
\(\displaystyle \delta = \frac{1}{c^2} \left(gh – vR \omega \cos \lambda – \frac{1}{2} v^2 \right)\)
où h désigne l’altitude, R le rayon de la Terre, \(\omega\) la vitesse angulaire de rotation de la Terre, et v la vitesse de l’avion : positive pour un voyage vers l’est et négative pour un voyage vers l’ouest. Intervient aussi la latitude \(\lambda\).
On retrouve bien ici l’influence gravitationnelle (le premier terme) et les termes cinématiques.
Un autre article amusant cité par Pierre Spagnou est celui de JM Lévy-Leblond,
Lévy-Leblond, J. M. (2015). Two new variations on the twins pseudoparadox. European Journal of Physics, 36(6), 065023.
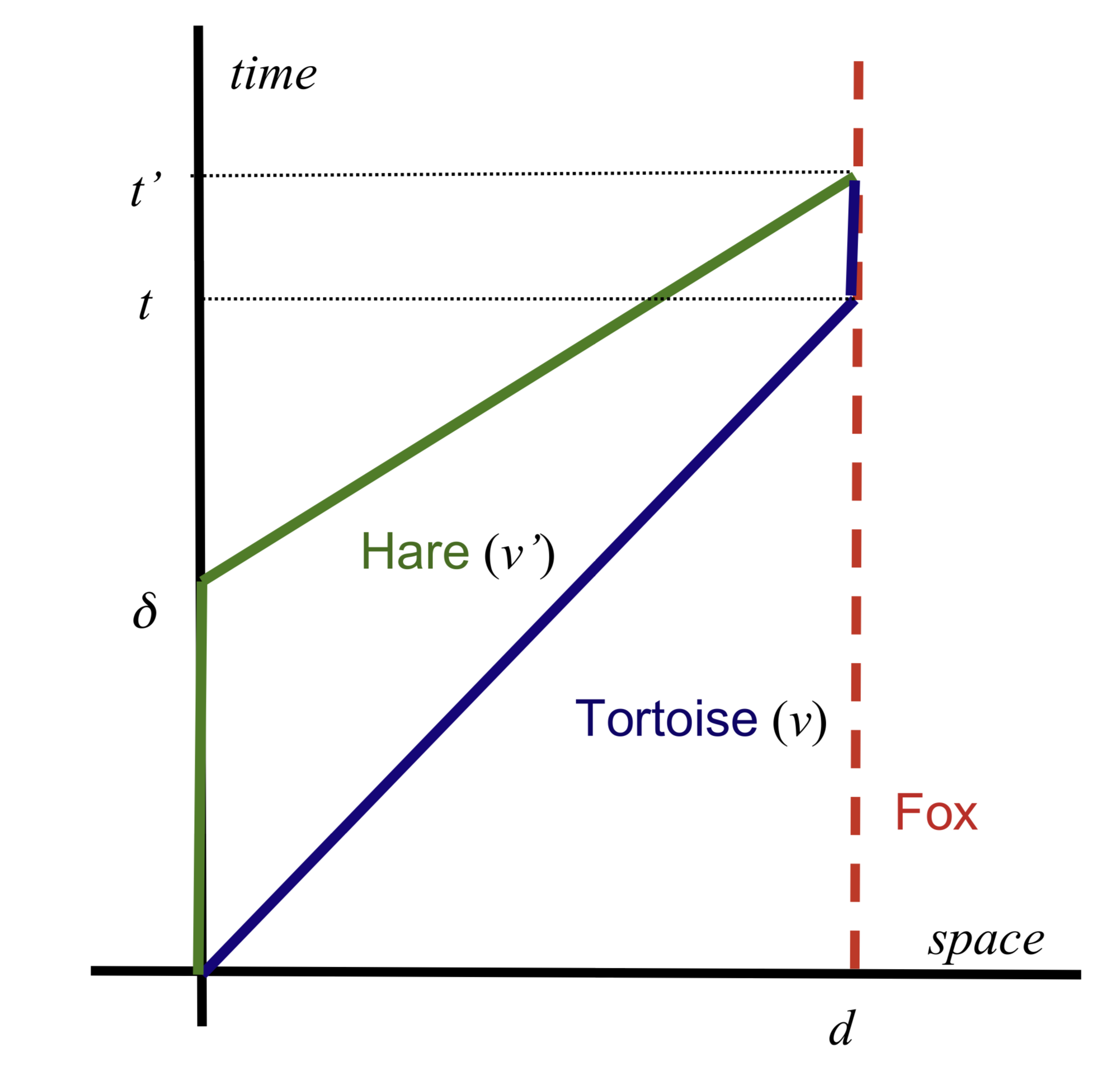
Dans cet article, l’auteur imagine une expérience du « Lièvre et de la Tortue » relativiste, dans lequel le lièvre part après la Tortue, arrive après elle. Le temps entre son départ et son arrivée sera jugé plus important par l’arbitre (le renard), mais le temps propre associé à la trajectoire du lièvre sera plus court que celui de la trajectoire de la tortue !
Version gravitationnelle
Dans la vidéo, j’ai brièvement présenté la version « gravitationnelle » du paradoxe des jumeaux, mais il s’agit bien d’un seul et même phénomène ! On peut unifier tout ça en introduisant la notion de métrique d’espace-temps \(g_{\mu\nu}\) et en écrivant que le temps propre s’obtient comme
\(\displaystyle \tau = \int \sqrt{g_{\mu\nu} dx^{\mu}dx^{\nu}}\)
En relativité restreinte, on utilise simplement la métrique « plate » de Minkowski \(\eta_{\mu\nu}\).
Dans le cas d’une métrique en faible champ gravitationnel (où l’on retrouve la gravité de Newton), le seul coefficient de la métrique qui se distingue de la métrique plate est le coefficient \(tt\) qui au lieu de valoir -1 (comme dans la métrique de Minkowski) vaut \(– (1+2\Phi)\) où on a \(\Phi\) le potentiel gravitationnel newtonien.
C’est ce terme \(tt\) qui provoque (en champ faible) la dilatation « gravitationnelle » du temps, mais également le fait de retrouver la loi de Newton. Et c’est en ce sens que ces deux phénomènes sont essentiellement dus à la « courbure du temps ».
Dans le cas général de la métrique de Schwarzschild (qui décrit notamment les trous noirs), on peut calculer le temps propre sur une trajectoire qui part de l’horizon pour aller vers la singularité.
Pour un objet qui commence au repos sur l’horizon des événements, le temps propre de chute est proportionnel à la masse du trou noir
\(\displaystyle \tau = \frac{\pi G M}{c^3}\)
Et c’est le temps propre maximal que l’on puisse espérer. Si au cours de la chute on essaye de freiner « pour tomber moins vite », on va en fait diminuer le temps propre de la trajectoire jusqu’à la singularité, étonnant non ?
Pour être tout à fait complet, notons que dans le cas général, si on croise l’horizon avec certaines trajectoires, alors la chute libre n’est plus nécessairement ce qui maximise le temps propre.
Lewis, G. F., & Kwan, J. (2007). No Way Back: Maximizing survival time below the Schwarzschild event horizon. Publications of the Astronomical Society of Australia, 24(2), 46-52.
https://arxiv.org/pdf/0705.1029.pdf
Et si on enlève tout ? Le principe de Mach
Maintenant je voudrai m’attaquer à une question un peu plus difficile, et pourtant que certains se seront posés : quand je dis que la situation n’est pas symétrique entre les deux jumeaux, pourquoi et-ce que ce serait le jumeau terrestre qui serait inertiel ?
La relativité restreinte (tout comme la relativité galiléenne) nous dit de façon un peu abstraite « il existe des référentiels inertiels », mais ne nous dit pas a priori comment les trouver ! Comme on sait qu’ils sont tous reliés par des translations rectilignes uniforme (ou des translations ou rotations fixes) : il suffit d’en trouver au moins un, et on les a tous. Ok, mais comment en trouve-t-on UN avec certitude ?
On a une définition expérimentale du référentiel inertiel : c’est un référentiel dans lequel les corps ne subissant aucune force ont une trajectoire rectiligne uniforme. Donc on peut expérimentalement en chercher un.
Le référentiel terrestre a l’air d’être un bon référentiel inertiel. Quand on fait des expériences, on remarque que c’est le cas. Sauf que dans certaines situations, on touche les limite. La terre n’est pas un pur référentiel inertiel du fait de sa rotation. Et cette rotation provoque des phénomènes mesurables : pensez au pendule de Foucault ou aux alizés, qui sont dus à la force de Coriolis.
Si on fait des expériences à des échelles de temps et d’espace qui font que la Terre n’est plus un bon référentiel inertiel, on peut se placer dans le référentiel héliocentrique, celui du Soleil. Mais lui non plus n’est pas un référentiel inertiel parfait, car le Soleil se situe sur le bord de notre galaxie, et effectue un mouvement de révolution autour d’elle en environ 250 millions d’années.
On peut continuer comme çà, mais la question demeure : qu’est-ce qui donne son caractère inertiel à un référentiel plutôt qu’à un autre ? En particulier, que se passe-t-il si on fait l’expérience des jumeaux dans un univers qui ne contiendrait absolument rien d’autre que nos deux jumeaux (pas de Terre, d’étoiles, de galaxies…) On aurait une situation en apparence parfaitement symétrique : qu’est-ce qui ferait que l’un serait plus inertiel que l’autre ?
La réponse à cette question se trouve être la même que celle d’une autre fameuse expérience de pensée : l’expérience du seau, imaginée par Newton et revisitée par Mach.
Prenez un seau rempli d’eau, et faites le tourner autour de son axe vertical. La surface de l’eau ne sera plus plate, et prendra une forme incurvée. Maintenant refaites cette expérience dans le vide absolu, en imaginant qu’il n’y ait plus ni Terre, ni étoiles, ni galaxies, rien. (et que l’eau reste gentiment liquide). Dans ces conditions, si on fait tourner le seau, il ne tourne plus par rapport à rien. Donc pourquoi la surface devrait s’incurver ?
La résolution de ce paradoxe, c’est de dire qu’en conditions normales, c’est la distribution de toute la matière de l’Univers qui fixe une notion absolue de « pas de rotation ». C’est donc cette distribution qui détermine ce qui est un référentiel inertiel, de ce qui n’en est pas un.
Dans le paradoxe des jumeaux, c’est pareil : le référentiel terrestre est (à peu près) inertiel du fait de sa vitesse relative par rapport au reste de la matière de l’univers, contrairement à la fusée.






70 Comments
Bonjour,
Merci pour cette vidéo et ce billet, et notamment merci d’avoir rétabli le fait qu’il ne s’agit pas d’un paradoxe, terme utilisé bien souvent à la légère.
J’aurais, si possible, une question. Elle n’est pas liée directement au sujet de la vidéo, si ce n’est par la notion de temps propre et de référentiel. Cette question concerne les paradoxes temporels. Mais avant de poser m question j’aurais besoin de préciser ce que je comprends à ce jour :
Il y a un temps propre, basé sur un référentiel. La causalité consiste à savoir comment sont reliés des événements dans le temps. Un temps propre signifie donc obligatoirement une causalité propre, car causalité sans temps n’a pas de sens. Il ne peut donc y avoir aucun paradoxe temporel : ce qui peut apparaitre à notre intuition comme un paradoxe est simple lié à une différence de référentiel.
Exemple : Le classique, je remonte le temps et je tue mon grand-père avant qu’il ne fase naitre mon père. On y voit généralement un paradoxe, dans le sens où ce serait censé empêcher ma naissance, je ne pourrais donc pas remonter le temps pour empêcher ma naissance, donc j’existerais, donc je pourrais remonter le temps pour empêcher ma naissance … … … .
Sauf que si on accepte la notion de temps/causalité propre il n’y a aucune contradiction. Je remonte le temps et je tue mon grand-père. Dans ma causalité personnelle je n’ai aucun besoin de ce grand-père pour naitre, je suis déjà né il y a x années. Dans le référentiel de mon grand-père il ne me fera jamais naitre mais n’en a pas besoin pour mourir, je l’ai déjà tué bien avant le moment où j’aurais du naitre.
L’illusion de paradoxe serait donc issue de notre intuition qui nous fait apparaitre le temps et la causalité comme universelle, ce que nous savons être faux.
Ma question est la suivante : Y a-t-il une incompréhension de ma part ? Je ne suis pas physicien, il y a de nombreuses choses que je ne connais pas, il se pourrait donc que je passe à côté d’une évidence. Est-ce le cas ?
J’y ajoute une question subsidiaire : s’il s’avérait que je n’ai aucune incompréhension pourquoi ce point de vue, lorsqu’il est question de paradoxes temporels, n’est pas seulement non-majoritaire, mais me semble même être inexistant dans les débats ? J’ai l’impression qu’il s’agit d’une conséquence simple et naturelle du temps propre, je ne comprends donc pas que tant d’autres hypothèses continuent à exister et à avoir tant de poids (encore une fois sauf incompréhension de ma part).
Les paradoxes temporels viennent d’une profonde incompréhension de la nature du temps et de beaucoup de fantasmes véhiculés par les films et les livres. En réalité la matière qui compose le objets et les êtres ne peut absolument pas se trouver à deux époques différentes dans le temps. Je l’explique (assez bien 🙂 ) dans un article sur le voyage dans le temps que j’avais écris sur Agoravox, et c’est sympa à lire, c’est ici :
https://www.agoravox.fr/actualites/technologies/article/le-voyage-dans-le-temps-175773
Bonjour,
Je te remercie pour ta réponse mais je la trouve malheureusement sans lien avec ma question. Je questionnais sur la causalité dans l’hypothèse du voyage dans le temps et non pas de l’hypothèse du voyage dans le temps lui-même.
De plus je t’avoue n’avoir absolument pas été convaincu par ton texte. Tu parles d’une vision du voyage dans le temps où le référentiel est une zone et où le temps propre monte à rebours, ce qui n’a rien à voir avec ce qui est communément appelé voyage dans le temps, et tu affirmes que c’est la seule chose possible. En dehors de ça je ne vois nulle démonstration.
Mais de toute façon ainsi que je l’indiquais même si ta démonstration avait été flamboyante à mes yeux je n’en aurais pas tiré usage, mon questionnement ne tenant pas à la crédibilité du voyage dans le temps.
Toutefois tu as vu ma question et tu as tenté de m’apporter quelque chose, je t’en remercie donc.
Mais justement Agaldian, « ce qui est communément appelé voyage dans le temps » comme tu dis n’est pas forcément « la vérité », cela pourrait parfaitement être un gros fantasme, et ça l’est bien sur, c’est ce que je défends dans l’article, le temps, comme bien des choses en physique, est « simple », enfin simple dans le sens « compréhensible » par l’esprit humain, ce n’est pas quelque chose qui est « hors de notre portée », car il y en a des chose comme ça, apparemment impossible à comprendre pour nous, et en tête : l’infini !
C’est vrai que le temps a une dimension infini, l’espace aussi. C’est encore une des choses qui me résiste et je ne sais pas par quel bout le prendre… L’infini, c’est même la seule « grande » question qui reste en physique, et il se décline dans tous les sens le petit coquin : dans le temps, donc, comment est-it possible qu’il puisse y avoir un début ? on peut toujours remonter avant… Et dans l’espace, bien sur, dans l’infiniment petit ou l’infiniment grand, « on peut toujours aller plus loin ».. cela défie l’esprit, il faut faire attention de ne pas devenir fou quand on travaille sur ça… Mais quand même, si je pouvais comprendre ça, l’infini, même un peu, avant de quitter ce monde… 🙂
Hoo mais.. l’infini ce n’est pas non plus ce que tu demandais… Pardon. Décidément, il ne faut pas parler avec des gens passionnés en physique, on arrive à rien vraiment 😀
Je te le confirme, je n’ai à nouveau aucun usage de cette réponse. Je te prie donc, s’il te plait, de ne plus intervenir sur mon commentaire.
Soit dit en passant tu ne défends rien dans ton article. Tu affirmes par le péremptoire. Il y a une grosse nuance entre ces deux choses. ‘Je connais la vérité ultime, c’est ça, et je le sais non pas parce que je m’appuie sur des théories scientifiques éprouvées ou sur des expérimentations mais parce que je le dis ».
Il est possible que ce que tu dis soit la vérité ultime. Je ne m’y oppose en rien. Mais il en va de même pour les milliers, voire les millions de personnes qui ont un avis sur le voyage dans le temps ou sur d’autres choses, comme l’infini. En venant en parler à quelqu’un qui n’a rien demandé ça signifie que tu estimes que je devrais m’intéresser à cet avis en particulier dont je ne suis pas demandeur et qui n’a à mes yeux aucune valeur ajoutée face aux milliers ou millions d’autres avis, d’autant plus ceux sans fondement.
Cela étant dit il y a probablement des gens qui postent ici ou sur youtube pour papoter. Toutefois si tu postes à l’aveugle il me semble que oui, tu seras à-priori souvent confronté à des gens obtus avec qui tu n’arrives à rien. Parce que ces gens peuvent trouver très facilement ce que tu viens apporter, et s’ils affirment un besoin autre, comme la recherche d’une réponse à une question précise, ce n’est généralement pas à l’aveugle.
Pardon mais vous me dites de ne plus intervenir mais vous contester mon article et je ne devrais pas avoir de droit de réponse ? Ce n’est pas très juste, si vous voulez que je ne réponde pas, ne lancé pas de controverse aussi…
Et en physique, quand on commence à étudier un phénomène on « affirme TOUJOURS par le péremptoire », forcément, et ensuite on réfléchit à la proposition, à l’idée, et on trouve ou pas que c’est « valide ». Quand Newton étudie la gravité universelle et comprend que la pomme est attirée par la terre il ne fait que « proposer » à tout le monde cette idée, de façon péremptoire, il ne PEUT RIEN prouver à l’époque évidemment, des gens aurait très bien pu lui opposer que la pomme est au contraire repoussée par le ciel (et si ça se trouve on lui a opposé cela), et même aujourd’hui ce n’est pas évident de le « prouver ».
Einstein n’a rien prouvé non plus quand il a « proposé » l’idée du 2 eme postulat, Maxwell non plus n’a rien « prouvé » quand il a proposé l’idée du courant de déplacement (avec laquelle je ne suis pas d’accord), une découverte scientifique c’est le règne du péremptoire bien sur. Et des idées.
Ensuite si tout le monde trouve que « l’idée » est bonne alors on commence a faire des expérimentations pour la vérifier et elle s’installe dans les esprits comme la « bonne idée ».
Voilà, il a fallu que je fasse un effort pour répondre et me défendre car je n’ai vraiment plus de plaisir à discuter avec vous, ce manque d’interet, d’humour, cette froideur inutile, me démotive totalement. Au départ je répondais (précisément ne vous en déplaise) à votre question « Le classique, je remonte le temps et je tue mon grand-père avant qu’il ne fase naitre mon père » car dans mon article j’explique précisément ce cas et donc je ne répondais pas « à l’aveugle » comme vous dites (notez que je ne me permet pas de vous tutoyer et merci d’en faire de même, nous sommes fort loin d’être intime !). Adieu donc j’espère.
Bonjour, merci pour ces discussions.
Je voulais souligner que vos façons de voir se rapprochent me semble-t-il !?
Fabien a peut-être un style professoral qui dépasse sa légitimité, et il semble aimer écrire des articles. Mais c’est de bonne guerre, et il sait que rien nous oblige à le croire. Néanmoins, s’il y avait eu une réponse apportant une vrai démonstration, il y a fort à parier que ni vous Algadian, ni Fabien, ni moi ne l’aurions comprise :). Faute d’être professionnels, nous en sommes réduit à quelques éléments de pensée.
Par contre, Fabien aborde bel et bien le sujet du paradoxe du voyageur dans le passé qui tue son parent. Il a une réflexion intéressante à ce sujet: dans l’univers il y a conservation de la matière. Comme l’ont expliqué des scientifiques : l’eau que nous buvons a déjà été uriné par les dinosaures ! (Ou la vidéo de Scienceétonnante : il y a dans mon verre une molécule déjà bue par Jules César !)
De ce fait, si je ne déforme pas trop les propos de Fabien, nous ne pourrons pas exister en « double » si un voyage dans le passé existe. Et cela correspond à ce qu’avance Algadian: si j’ai bien compris, chacun gardant son référentiel. Certes, le grand-père ne permettra pas la naissance du père, ni donc d’un petit fils. Mais pour ce dernier, qui a réussi à trouver un système pour s’incruster dans ce temps passé : cela ne change rien… il y est, il y reste ! 🙂
En fait, le plus étonnant serait qu’en s’incrustant dans le passé il ne change rien ! Il y a tout un tas d’effets papillon qui pourrait faire rater la rencontre de ses parents, ou bien.. le soir de sa conception un parent aurait une migraine… qui repousserait la conception au lendemain. C’est à dire avec un autre spermatozoide vainqueur.. et donc la naissance d’un frère, et jamais de lui-même !…
Meurtre de son grand-père ou non, il faut avouer que le cas où tout se passe identiquement au millimètre près (au micron près), est finalement le moins probable. C’est un peu ce qui dit Fabien aussi.
Mais si on en revient à la remarque concernant la quantité de matière : Fabien, vous imaginez qu’un retour dans le passé pourrait consister à « rembobiner » le monde, instant par instant, sauf le voyageur qui serait dans la machine (et donc serait absent du « film » se rembobinant sans lui.)
Ceci paraît effectivement « conserver la matière » … sauf que, si le voyageur sort de sa machine à l’époque où il était bébé : il ne peut exactement remplacer celui-ci dans l’univers…car il emmène trop de matière par rapport au bébé qu’il était. Sans compter que les cellules qui nous composent ont leur histoire propre, et ne sont pas les mêmes que celles qui nous composaient étant bébé. On ne peut donc pas s’isoler d’un côté et rembobiner le reste du monde par ailleurs. Des électrons, des cellules qui nous composent étaient utiles à d’autres (hommes, animaux, plantes, …).
Le problème est identique avec des univers parallèle : problème de conservation de la matière si on passe de l’un à l’autre.
Ce n’est pas cet argument qu’utilise Fabien, mais il considère aussi que les voyages dans le passé ne sont pas possibles. Et cela constitue aussi une réponse à votre question Agaldian: on ne peut pas théoriser sur quelque chose d’impossible. Bien sûr, je crois comprendre que vous n’êtes pas sensible à cet argument et considérez les voyages dans le passé comme possible. Mais à partir du moment où vous posez la question chacun vous répond selon ses convictions. D’ailleurs Einstein persista toute sa vie à croire au principe de causalité. Bien sûr, on a vu qu’il avait tort à ce sujet concernant la physique quantique. Mais proposer la vue d’Einstein pour l’échelle humaine ne paraît pas stupide.
il n’en reste donc pas moins qu’une réponse à tes questions Agaldian, peut très bien être que les voyages dans le passé sont impossibles.
Bonne soirée
Maxime vous avez presque tout compris 🙂 juste à un moment vous dites : « si le voyageur sort de sa machine à l’époque où il était bébé : il ne peut exactement remplacer celui-ci dans l’univers… » mais justement, à ce moment, s’il sort de la machine, il n’y aura pas de bébé qui serait lui-même à cette époque, la matière du voyageur n’est pas revenu dans le temps donc elle n’est pas « redevenu » bébé… Et pire comme le monde est revenu en arrière sans les actions « à l’envers » du voyageur le monde tout entier est différent… C’est une sacré gymnastique d’imaginer tout ça mais une fois qu’on a pris l’habitude ça roule tout seul et il n’y a plus le moindre paradoxe, ça devient presque trivial, le temps, alors que c’était éligible pour être un des phénomène inabordable pour notre conscience…
L’infini ça, ça reste une de mes grandes interrogation ! Ca c’est vraiment pas facile… Pire que la constante de structure fine… La seule pseudo solution que j’ai trouvé (et encore seulement pour l’infini de l’espace parce que pour celui du temps c’est juste impossible apparemment 😐 ) c’est qu’à un moment, à une limite, quand on avance très loin dans l’univers, et bien il n’y a plus rien.. voilà, et le « rien » de cette ampleur, vraiment rien, et bien ça n’a plus de « dimension », donc ça n’est pas infini, c’est « rien », le néant… Par contre quand on avance dans ce « rien » ça se construit, avec de la matière, ça prend de la « dimension », on peut objecter qu’on peut le faire de façon infini et que donc la question continue de se poser et c’est vrai en théorie mais en pratique !? Et oui, en pratique on ne peut rien faire de façon « infini », on ne peut pas « avancer de façon infini » en pratique, de la même façon on ne peut pas réellement compter jusqu’à l’infini, c’est juste en « théorie » qu’on voit que c’est « possible », en pratique niet… Bref, ça reste ouvert mais c’est un truc comme ça je pense 🙂
Vidéo géniale (comme d’hab). Suite à la lecture de votre billet, je me pose une question fatidique. En observant un astre situé à 4 années lumière de nous. L’image que nous recevons correspond elle, temps pour temps, à ce qu’elle était il y a 4 ans en arrière ? Plus clairement, tenons nous compte de la notion de paradoxe lorsque nous estimons une distance dans l’espace ? Merci beaucoup
Je vais tenter une réponse simple (peut-être fausse désolé) : sans doute que les scientifiques considèrent l’espace-temps comme étant presque (et non pas strictement) vide dans les calculs de longue distance. Il doit s’agir d’une moyenne, et donc de la célérité c de la lumière dans le vide, considérée comme constante. Oui, un astre situé à 4 années lumières est vu, grâce aux photons, comme il était il y a 4 ans, à quelques approximations près (je crois que le paradoxe implique un « aller-retour » et une comparaison entre objets macroscopiques)
Merci. En fait j’avais fait une analogie entre les jumeaux et les photons. Mais peut être que cette comparaison n’a guère de sens. C’est pour cela que je me demandais si le temps parcouru par la lumière était réellement absolu ou si il subissait la même « déformation » que le jumeau voyageant d’un point à un autre de l’espace.
Les photons qui nous parviennent ont voyagé à la vitesse de la lumière, dans leur temps propre, ils se sont « téléportés » jusqu’à nous.
Pour nous, ils ont parcouru 4 AL en 4 ans. L’image que nous recevons est donc bien une image qui a 4 ans « pour nous ». Mais ce n’est pas l’image de ce qu’était l’étoile il y a 4 ans, dans le sens ou cette notion de simultanéité n’a pas de sens : au moment où on regarde l’étoile, l’image qu’on en a c’est ça qui est simultané pour nous. ça n’a pas de sens de se demander à quoi elle ressemble « maintenant » : pour nous, elle ressemble à ce qu’on observe « maintenant ».
C’est le même soucis que le jumeau qui se demanderait quel âge a son jumeau « maintenant » : il n’y a pas de référentiel de temporalité universel, donc on ne peut pas savoir tant qu’ils ne sont pas réunis.
Bonjour,
Merci beaucoup pour cette vidéo. Cependant, une question m’a toujours turlupiné à propos du paradoxe des gémeaux. Je l’ai posé en commentaire sous la vidéo mais j’aurai plus de chances d’avoir une réponse ici.
« Comment lève-t-on le paradoxe si l’on suppose que le jumeau suit une géodésique non triviale (c’est-à-dire qu’il part de la Terre avec une certaine vitesse et y retourne en un temps t>0 sans jamais subir la moindre accélération) ? La situation me semble alors parfaitement symétrique.
Je veux bien qu’on me dise que ce n’est pas possible, mais il me semblait que c’était le principe des trous de vers. J’ai essayé de trouvé une réponse à ce paradoxe (qui porte le nom de « Paradoxe des jumeaux cosmologique », je crois), mais je ne les ai jamais comprises ! »
J’ai trouvé une référence qui parle de ça depuis que j’ai rédigé ce commentaire (qui reprend, d’après l’abstract et ce que je peux en juger, des explications que j’avais trouvé sur un forum). Je vais essayé de m’y replonger, mais je n’avais pas compris à l’époque :
https://arxiv.org/abs/gr-qc/0101014v1
PS.: J’ai une formation de maths, pas de physique, ce qui explique sans doute pourquoi je galère.
Bon, ben… en la réponse d’Erwan ci-dessous, j’ai appris que le sujet était évoqué dans le billet (ça m’apprendra à lire en diagonale), avec des références et une promesse d’explication ! J’ai l’air malin tiens.
Bon, j’ai lu le « Twin paradox and space topology » mais il y a toujours des points mystérieux pour moi :
1) L’espace-temps peut s’écrire M = R x Σ = R x (X/Γ). Jusque là, d’accord, mais « If Γ reduces to the identity, space is simply–connected, in the sense that two points of space are connected by only one geodesic » : ce n’est pas la définition d’une variété simplement connexe… Les sphères S^n sont simplement connexes pour n>1 (d’ailleurs rien n’empêche X = Σ = S³) et tous les points antipodaux sont reliés non pas par une géodésique, ni même un nombre fini de géodésiques, mais par tout un continuum de géodésiques ! Pourtant, l’article ne semble considérer qu’au plus un nombre fini de géodésiques minimales sur Σ et ne semble pas s’intéresser du tout à la topologie de X.
2) Ce problème s’aggrave lorsque l’on considère un cas comme Σ = P³ = (S³/Z₂), où Γ consiste à identifier les points antipodaux. Dans ce cas, le groupe fondamental de Σ est Z₂, c’est-à-dire que l’on a une géodésique γ telle que γ ≁ {0} mais γ² ~ {0} : le « winding index » d’un jumeau 0 resté sur Terre est le même que celui d’un jumeau 2 ayant fait deux fois le tour via une géodésique mais n’est pas le même que celui d’un jumeau 1 n’ayant fait qu’une fois le tour. Comment départager alors ?
Bon, c’est deux problèmes sont tellement énormes qu’il s’agit forcément d’un truc énorme que je n’ai pas compris et qui justifie de se limiter aux topologies données par la figure 1 de l’article (et leurs généralisations en dimension 3).
3) « [C]utting and pasting to compactify the spatial sections defines (i) particular directions, so that space, even if locally isotropic, is no more invariant under rotations, and (ii) a particular time: the one measured by an observer whose 4–velocity is perpendicular to Σ ». Si je comprend bien cette étape, il s’agit de prendre des cartes locales de Σ engendrées par les vitesses des jumeaux 3 et 4 en t=0. Si l’espace Σ est compact (ex. : un tore), alors on a suffisamment de géodésiques pour former une base locale et donc fixer un axe du temps particulier. Cependant, si l’espace Σ n’est pas compact mais non-euclidien (ex. : un cylindre), alors on a moins de géodésiques et on ne peut pas fixer un axe du temps particulier, seulement un sous-espace strict de M particulier contenant les axes du temps de tous les référentiels. Ça ne pose pas de problème pour le reste puisque les directions de M qui sont distinguées par ce processus sont précisément celles qui requièrent une distinction pour le reste de l’article (en particulier pour les « winding indices »).
Est-on bien d’accord tout de même que l’article montre que la compacité de Σ définit un référentiel inertiel privilégié, mais que l’on ne peut pas être sûr que la Terre est ce référentiel privilégié plutôt qu’une fusée empruntée par le jumeau 3 ou 4 ? Dans l’article, le problème est esquivé, je crois, en considérant des événements O et P de M plutôt que le vaisseau Terre.
4) Dernier point, promis. Est-il possible que la topologie de l’univers observable soit différente de la topologie de l’Univers ? J’imagine que oui puisque les distorsions de la métrique de l’Univers peuvent ‘aller plus vite’ que la vitesse de la lumière (c’est un réponse à l’interrogation de Myrkiriad ci-dessous). Ça ne pose pas de problème qu’une expérience conduite par les jumeaux 1, 3 et 4 de l’article – expérience qui se déroule strictement à l’intérieur des univers observables des protagonistes – puisse renseigner sur la topologie hors de l’univers observable ? En particulier, si je ne dis pas de bêtise, cette expérience pourrait déterminer si le jumeau 3 est plus jeune à cause de la topologie de l’Univers ou s’il a juste tourné autour d’un objet extrêmement massif situé hors de son univers observable (arrivé à la fin de cette phrase, j’ai complètement perdu l’espoir de ne pas avoir dit une bêtise que j’avais au début, mais je ne vois pas l’erreur…). En gros, on pourrait distinguer entre les deux situations suivantes alors que l’univers observable (orange) ne suffirait pas à priori à décider de la topologie de l’Univers (bleu ciel).
https://imgur.com/fxvU45Q
Pardon pour le pavé ; j’espère n’avoir pas enfilé que des perles et qu’il y a quand même quelques difficultés réelles dans ce que je ne comprends pas !
Non Arthur je ne suis pas en accord avec tes dernières conclusions : Si l’étoile dont on parle n’a pas de vitesse relative par rapport à toi sur terre, il est parfaitement possible de parler de son état réel il y a 4 ans et d’extrapoler son état pour maintenant car dans ce cas tout ce passe dans le même référentiel.(le référentiel de l’étoile est le même que le tien). En fait dans ce cas , on peut raisonner tout a fait naïvement sans invoquer théorie de la relativité, c’est juste le messager qui prend du temps pour arriver, mais ce serait pareil avec une onde sonore ou la poste .
Merci pour cette nouvelle vidéo encore une fois de grande qualité !
Je me pose la question du paradoxe des jumeaux dans un espace fini depuis un petit bout de temps :
Je suis impatient d avoir plus de détails dessus comme tu le mentionnes dans cet extrait de ton article
» topologies non-triviales (disons un tore) et donc le fait que le jumeau de la fusée puisse revenir au point de départ et retrouver son frère sans avoir jamais du faire demi-tour ! »
Je n’ ai jamais réussi à trouver une vulgarisation sur ce sujet.
J’avais un prof en TD de relativité restreinte qui nous avait expliqué ce paradoxe avec les mains, mais dans le cadre du cylindre (c’est le même problème que celui du tore, d’ailleurs l’article cité « The twin paradox and space topology » en parle aussi, mais est un peu plus simple à se représenter):
Si on prend le diagramme d’espace temps de la vidéo (par ex. à 17:28), et qu’on replie la dimension d’espace, en considérant que la ligne x=8AL est équivalente à la ligne x=0AL, le « nouveau » paradoxe est que si le jumeau de la fusée continue tout droit sur sa trajectoire, il retrouvera quand même le jumeau de la terre après 12 ans (pour un observateur terrestre), et n’aura vieilli que de 9 ans. Pourtant, rien dans les trajectoires ne permet à priori de distinguer les deux jumeaux, vu que la fusée n’a jamais fait demi-tour.
En fait la solution de ce paradoxe est que c’est la topologie choisie qui casse la symétrie: quand on dit que x=8AL est équivalent à x=0AL, on veut en fait dire que les évènements qui ont lieu simultanément en x=0AL et en x=8AL sont identiques. Mais quand on parle de simultanéité, ça veut dire qu’on a déjà choisi un référentiel particulier: ici celle du diagramme d’espace temps que l’on a considéré, le référentiel terrestre. Ce repliement n’a pas du tout la même tête si on cherche à le représenter sur le diagramme d’espace temps de la fusée.
Le plus drôle, c’est que le prof de TD en question était un certain Roland Lehoucq, et que c’est après 10 ans et grâce à ce blog que je découvre qu’il avait publié sur la question quelques années plus tôt… :p
Je prends le risque de répondre, mais je précise que je ne suis pas un professionnel ou un étudiant en physique/maths.
D’après mes propres recherches et réflexions, j’ai conclu que la notion d’accélération est inévitable en physique : elle symbolise le mouvement le plus fréquent, qui sous entend une interaction (car une bulle d’espace-temps sans aucune énergie est elle possible ?). La topologie non-triviale dont vous parlez semble être un objet mathématique. C’est peut-être physiquement possible, mais je vous conseille de vous méfier des objets mathématiques purs (ils aident à comprendre mais c’est une simplification, parfois complexe !, du réel).
Avant d’entrer dans le vif du sujet, je précise qu’il s’agit de réflexions plus proches de la métaphysique que de mathématiques physique.
Il y a un postulat (sorte d’axiome) qui considère la valeur c comme étant une limite physique maximale de déplacement dans l’espace-temps. Le photon, quantum de lumière, est attribué à c. Mais pourquoi la lumière aurait elle un caractère absolu? Pourquoi pas une particule virtuelle, entre corpuscule et onde? Je propose d’inclure la notion de spectre de valeur (échelle de valeur) avec des nombres entre une forme la plus corpusculaire possible et une forme la plus ondulatoire possible (il se peut que ces notions d’ondes et de corpuscules soient entièrement à revoir). L’objet le plus corpusculaire pourrait être au centre d’un trou-noir tandis qu’un objet le plus ondulatoire possible pourrait être une particule virtuelle. Il est possible qu’une particule virtuelle aille plus vite que c dans le vide (mais ce serait une limite indépassable, c’est le déplacement absolu d’une onde dans le vide). Cette onde est intemporelle (donc sans masse, càd sans volume d’énergie dans un lieu donné et à un moment donné).
Une autre notion qui rejoint l’idée du spectre de valeur (pour avoir une alternative au concept d’espace en mètres et de temps en secondes). Ce serait la notion de mesure référentielle. Celle-ci est un nombre qui dépend du référentiel : tous les objets du même référentiel auraient la même mesure interne (une sorte de vitesse interne en fait). Plus le déplacement est rapide ou soumis à une gravité forte, plus la trajectoire spatio-temporelle sera courte (le temps propre), et plus le nombre de la mesure référentielle est important. Des objets ayant la même mesure référentielle sont classés selon le nombre associé au spectre de valeur entre le corpuscule absolu et l’onde absolue. Choisir la valeur de cette mesure référentielle dépendrait du degré de vieillissement (nombre de désintégrations d’une catégorie d’atomes, nombre de cycles biologiques, etc). Ou alors créer un instrument de mesure capable de distinguer le degré ondulatoire et corpusculaire, en mesurant la densité de masse (un corpuscule a une densité de masse plus élevée qu’une onde). Il s’agit d’idées purement théoriques pour remplacer les notions d’espace et de temps (mais je suppose que c’est innapplicable pour faire de la physique expérimentale).
En tous cas, merci David pour ta vidéo très claire (le temps propre est important à comprendre). J’ai même auparavant consulté bon nombre de tes vidéos et blogs (mais je n’avais pas de compte youtube). J’espère que tu vas continuer à nous faire partager tes connaissances !
Pour ce qui concerne le caractère maximale de c c’est plus une certitude qu’un simple postulat en réalité, cela découle directement des équations de l’électromagnétisme si je ne dis pas de bêtise. Comme vous l’avez très bien fait remarqué pourquoi la vitesse d’un photon et pas d’une autre particule ? et bien la réponse est, comme souvent en physique, la plus simple, on s’en moque du photon, on peut regarder un muon, un kaon ou un électron dans un atome leurs célérités atteignent toutes la fameuse valeur c. Je suppose que l’on a gardé le nom de vitesse de la lumière parce que c’est la plus parlante pour le grand publique et que c’est certainement la première que l’on est pu mesurer avec certitude)
Attention, la constance de c ne « découle » pas des équations de l’électromagnétisme, Maxwell a « introduit » un phénomène (qu’il a totalement imaginé) le courant de déplacement, et il l’a ajouté dans les équations d’électromagnétismes classiques (Ampère/Faraday) ce qui a permis d’introduire le temps, et du coup une vitesse, ce qui est plus que fumeux et en tout cas ne « prouve » rien du tout…
Mais cette pirouette mathématique en physique, comme c’est souvent le cas de nos jours où tout est « expliqué » par des maths, plus rien par des « mots » (sauf dans les vidéos de David ! 😉 ) a finalement été accepté par tout le monde car expérimentalement on a constaté que la vitesse de la lumière était toujours c plus ou moins partout où on pouvait l’observer. Mais ce qu’il n’ont pas compris (ce que je défends) c’est que la lumière, les ondes électromagnétiques, changent de vitesse très facilement, après une simple réflexion sur un miroir par exemple quand elles arrivent à toute vitesse de l’espace… Leur vitesse est extrêmement « fragile » on pourrait dire.
En fait les ondes électromagnétiques sont émise (ou ré-émise) par la matière à exactement la vitesse c donc on calcule partout cette vitesse et on croit que c’est pareil dans tout l’univers.
Pourtant il y a de nombreux indices qui prouvent que dans certains cas on a à faire a des ondes électromagnétiques qui vont plus ou moins vite que c, et en tête Pioneer 10, comme on le voit dans l’article sur vixra par exemple :
https://vixra.org/pdf/1904.0121v1.pdf
Merci pour vos explications !
Très bonne vidéo ( accompagné du billet ) qui donne une super compréhension de l’origine de l’asymétrie des deux référentiels de ce paradoxe.
Une question cependant me turlupine. Si l’on fait l hypothèse d’un univers fini sans bords alors il serait possible pour la fusée, après l’accélération initiale, de revenir a son point de départ sans changer de direction. Quel serait le résultat de cette expérience ? A-t-on toujours une asymétrie ?
Une chose que j’ai du mal comprendre :
Mon prof de physique à la fac nous donnait l’exemple suivant :
-prenez une table plate avec un trou circulaire en son centre (supposer immobile dans une référentiel Galiléen)
-prenez une plaque ayant exactement les même formes, taille et épaisseur que le trou de la table
-positionnez vous à la verticale du trou et décalez vous d’une distance non nul
-envoyez la plaque en visant parfaitement le trou de la table (et en veillant à ne lui donner aucune rotation de façon à ce qu’elle arrive parfaitement coplanaire à la surface de la table)
-à cause de l’épaisseur combiner à l’angle d’approche, la plaque ne devrait pas pouvoir passer à l’intérieur du trou pourtant on peut y arriver, comment ? en l’envoyant à une vitesse remarquable devant celle de la lumière
-la conservation de la distance d’espace-temps fait que la plaque franchira le trou sans problème
et c’est là que je ne comprend pas, une fois que la plaque a atteint la vitesse voulu, elle ne subit plus d’accélération et se retrouve donc dans un référentiel Galiléen au même titre que celui de la table. Il n’y a donc aucune asymétrie des référentiels et j’ai du mal à comprendre en quoi c’est la plaque qui voit ces longueurs contracter afin qu’elle passe et non la table qui se contracte mettant un terme à toutes chances de faire passer la plaque ?
Dernière phrase du blog: « Dans le paradoxe des jumeaux, c’est pareil : le référentiel terrestre est (à peu près) inertiel du fait de sa vitesse relative par rapport au reste de la matière de l’univers, contrairement à la fusée. »
Je ne vois pas en quoi la vitesse relative de la terre est significativement différente de celle de la fusée par rapport à la matière de l’univers. Du fait de l’expansion de l’univers, n’y a-t-il pas quantité de matière qui s’éloigne de nous à des vitesses proche de celle de la lumière ? Du coup, on trouve tout le spectre de vitesse relative par rapport à la matière de l’univers que ce soit pour la terre ou la fusée.
Bonjour,
pour ce qui concerne l’inclinaison du temps, vous ne donnez pas d’interprétation. Vous parlez de l’estimation de l’âge de la Terre par le jumeau dans la fusée. Puis vous dites que tant qu’ils ne sont pas réunis parler de leur âge relatif n’a pas de sens. Le fait que la Terre ait 3 ans puis 9 ans pour le jumeau dans la fusée a une réalité ou n’en a pas ? Si le jumeau de la fusée pouvait téléphoner à une personne de son propre référentiel situé en face de la Terre celui lui décrirait bien une terre plus jeune dans le premier référentiel puis une terre plus vieille dans le deuxième.
Le problème vient peut-être du fait que ce plan avec ses coordonnées de temps et d’espace ne fonctionne pas comme un plan euclidien ; on le voit quand David trace les lignes de simultanéité pour le jumeau de la fusée (// à l’axe de temps dans son référentiel). Il faut prendre cela comme un échiquier avec ses règles de déplacement spécifiques. Je n’en dirais pas plus car cela fait plus de 40 ans que je ne les ai pas maniés et je risquerai de dire des bêtises sur les métriques pseudo-euclidiennes et l’espace-temps de Minkowski.
J’ai tenté de répondre à votre question mais je ne suis pas totalement sûr de ma réponse et surtout de sa clarté : le jumeau de la fusée téléphone quand il est sur Proxima avant de faire demi-tour. Ce n’est pas instantané : il faut 4 ans pour que les ondes électromagnétiques transmettant son message arrivent sur Terre (Proxima est à 4 AL de la Terre). Donc il se dit à son premier coup de fil qu’il se sera écoulé 3,3 + 4 = 7, 3 ans sur Terre quand son jumeau décrochera le téléphone (je suppose 3,3 ans au vu du graphique). Pour le jumeau terrestre, puisque l’autre lui a téléphoné à proximité de Proxima il reçoit le coup de fil quand il s’est écoulé 6+4 = 10 ans (4 ans aussi puisque la vitesse de la lumière est la même dans tous les repères).
Puis après son freinage son demi-tour et son accélération, qui ne peuvent être instantanés, disons qu’il s’est écoulé quelques semaines, il appelle à nouveau et pour lui à ce moment la Terre est à environ 8,8 ans du départ. Donc le jumeau de la terre recevrait son coup de fil à 8,8 + 4 = 12,8 ans après son départ. Déjà ça coince parce qu’à cette date, il est déjà revenu sur Terre.
Son calcul ne marche pas car il additionne un temps propre qui correspond à une (enfin deux) trajectoires réelles – le temps entre l’envoi du coup de fil à Proxima et sa réception sur Terre soit les 4 ans de trajet – et un, enfin deux, temps qui ne correspondent pas à un intervalle entre des évènements réels, mais à des calculs de simultanéité, des droites non physiques qui donnent 3,3 puis 8,8 ans.
Le seul évènement réel est l’envoi de ses messages au moment où il atteint Proxima. La trajectoire est celle de ses messages et pour le jumeau sur Terre, si je ne me trompe pas, ces messages arrivent 6+4 = 10 ans (+ quelques semaines) après le départ (second évènement). Et le jumeau terrestre lui donnera ce temps.
Bonjour, merci pour votre réponse. Je comprends que le coup de tel ne peut pas être instantané. Mais mon point était un peu différent. La constance de la vitesse de la lumière entraîne une contraction des distances, une dilatation du temps et une inclinaison du temps. Or pour pour les 2 premiers effets, on peut toujours citer des expériences qui les ont démontrés. Mais pour l’inclinaison du temps, on a l’impression que tout le monde se défile. David parle d’estimation, l’auteur des idées froides parle d’un effet de perspective. C’est cela que je ne comprends pas. Si l’inclinaison du temps fait bien partie de la théorie, alors on peut l’utiliser pour calculer ce qu’indique les 2 horloges des jumeaux à tout moment. Pourquoi dire que tant qu’on a pas réuni les 2 jumeaux essayer de comparer leur horloge n’a pas de sens ? Ce que je comprends de l’inclinaison du temps c’est qu’un observateur appartenant au référentiel de la fusée (donc synchro avec le jumeau de la fusée) et qui se trouverait en face de la Terre verrait bien le jumeau sur Terre plus jeune. Puis après le demi tour, le jumeau de la fusée change complètement de référentiel. Il est alors synchro avec un observateur qui se déplacerait dans l’autre sens à la même vitesse. Et pour cet observateur en face de la Terre le jumeau terrestre serait bien plus vieux.
» vous dites que tant qu’ils ne sont pas réunis parler de leur âge relatif n’a pas de sens »
puis :
» Pourquoi dire que tant qu’on a pas réuni les 2 jumeaux essayer de comparer leur horloge n’a pas de sens ? »
Vous trouverez la réponse à votre interrogation dans, d’une part, l’axiome » Les horloges physiques mesurent le temps propre » ( paragraphe » Temps propre et temps des coordonnées ») et ,d’autre part, dans l’analogie euclidienne illustré par un dessin et expliquée dans la paragraphe » Accélération » . Dans le cas euclidien, on ne peut comparer utilement des distances parcourues le long de deux trajectoires distinctes QUE SI ces trajectoires ont des points extrêmes communs ( même point de départ et même point d’arrivée ) . Si deux « voyageurs » partent d’un même point et si leurs trajectoires respectives ne concourent plus jamais ensuite, que peut-on comparer utilement ? Dire que la distance parcourue par l’un est plus grande ou plus petite que la distance parcourue par l’autre n’a aucune pertinence si le point de départ est le seul point de concours des trajectoires . OK ?
L’analogie euclidienne que Didier Louapre a faite dans son texte est une excellente idée . C’est d’ailleurs bien plus qu’une analogie « illustrative », il y a une vraie parenté mathématique : Les aspects cinématique du modèle de la relativité restreinte sont régis par la métrique de Minkowski et la « distance » associée est la variation de temps propre , tout comme les propriétés de la distance que nous qualifions communément d’euclidienne sont régis par la métrique … euclidienne, justement . En toute rigueur, il faudrait remplacer le terme familier ( et trompeur) de « droite » par la notion de géodésique, et remplacer la notion de « virages » par quelque chose du genre « écart à la géodésique » . Mais bon, je pense que Didier Louapre a bien fait de privilégier une présentation des choses un peu moins technique ici …
Bonjour, merci je viens de comprendre. Chacun des jumeaux peut bien calculer à tout moment dans son propre référentiel l’âge de son frère. En revanche ce que l’on peut pas faire c’est dire l’âge de chacun des jumeaux en ce moment tant qu’on ne les a pas réunis parce que « en ce moment » n’a pas de sens.
David l’explique très bien (c’est mon cerveau qui est lent) en prenant l’exemple du « moment » du 1/2 tour. Ce moment a lieu quand le jumeau sur Terre a 6 ans (pour le jumeau sur Terre) et quand le jumeau sur Terre a un peu plus de 3 ans pour le jumeau dans la fusée. Du coup effectivement se demander quel est l’âge des jumeaux au moment du 1/2 tour n’a pas de réponse absolue. Ça dépend pour qui.
Merci pour votre réponse . Si l’analogie euclidienne vous a aidé à éclaircir les choses, je ne saurais trop vous recommander d’approfondir cette analogie LE PLUS que vous pouvez . C’est plus qu’une analogie « ordinaire » ( car, mathématiquement, c’est très semblable) . Cette « analogie » est très utile pour éclaircir de nombreux aspects QUALITATIFS de la relativité restreinte. Par contre les conclusions QUANTITATIVES pourront être différentes . Un exemple illustrera mon propos :
Dans un espace métrique euclidien, entre deux points fixés, c’est la géodésique qui réalise le MINIMUM de distance ( le « plus court chemin entre deux points » ) . Dans un espace métrique minkovskien, la « distance » définie par la métrique est la variation de temps propre et une géodésique réalise le MAXIMUM de la « distance » entre deux points fixés . Pas de soucis à ce sujet, ces propriétés se démontrent ( d’ailleurs, pour ces DEUX propriétés, on peut mettre sur pied deux démonstrations « jumelles », bâties sur les même principes mathématiques, exactement ) . Donc dans les deux cas euclidien et minkowskien les aspects QUALITATIFS sont semblables ( la géodésique réalise un EXTREMUM de la distance entre deux points fixés ), par contre la nature QUANTITATIVE de l’extremum en question sera opposée ( minimum dans un cas, maximum dans l’autre ) .
L’analogie euclidienne est également utile pour comprendre le rôle joué par la transformation de Lorentz dans toutes ces histoires . Une telle transformation de coordonnées est une transformation ISOMETRIQUE pour la métrique de Minkowski, c’est à dire qu’elle CONSERVE l’expression du tenseur métrique . En effet, lorsqu’on change de système de coordonnées, l’expression d’un tenseur métrique doit être recalculée, et en général ce ne sera plus la même … SAUF si la transformation de coordonnées est ISOMETRIQUE justement .
Faisons alors l’analogie euclidienne (2D ou 3D, mais 2D est plus simple pour commencer ) : quelle est la transformation qui va jouer un rôle analogue a la tr. de Lorentz ? C’est la rotation, bien sûr ! Une rotation conserve le tenseur métrique euclidien ( Dans la littérature, vous trouverez souvent une formulation du genre « une rotation appliquée aux coordonnées conserve la distance », je n’aime pas cette formulation pour des raisons que je ne détaillerai pas ici ) .
On peut donc s’inspirer de l’illustration 2D du texte de David Louapre, en effaçant les segments de courbes ( et de droite ) et en illustrant à la place deux axes de coordonneés horizontal et vertical appelés « X « et « T »( oui « T », histoire de faire penser à la coordonnée « temps » présente dans le cas minkowskien … ) . Le nouveau système de coordonnées, mettons X’ et T’ , sera obtenu par la rotation d’un angle donné appliquée aux axes de coordonnées X,T . Prenons un point origine commun « O » pour faire simple, les nouveaux axes OX’, OT’ seront chacun « inclinés » par rapport aux anciens OX,OT . Si, par la pensée, on attribue à T et T’ les rôles de « dimension temps » dans leurs systèmes respectifs, on voit que la simultaneïté, c.a.d. la notion de « iso-temps » sera un « iso-T ( soit une droite horizontale ) dans l’ancien « repère », et un iso-T’ ( c.a.d une droite inclinée ) dans le nouveau repère . La « simultaneïté »est donc relative au « référentiel » .
Bien entendu, on peut faire tourner la page autour du point O de façon que les nouveaux axes soient horizontal/vertical et les anciens soient inclinés, histoire d’illustrer la SYMETRIE du probleme . Si on a pris soin de dessiner une courbe d’égale distance euclidienne à l’origine O, autrement dit … un cercle, ce cercle sera globalement inchangé par la rotation de la page autour de O .
Justement, cette dernière remarque illustre les limites … GRAPHIQUES ( mais non mathématiques) de l’analogie euclidien/minkowskien . Si on prend un cas minkowskien simplifié avec une seule dimension spatiale, mettons X ( on n’a alors que 2 dimensions : X et T ) . On peut toujours dessiner sur une page deux axes orthonormés OX ( horizontal) et OT ( vertical ) . Si on a pris soin de fixer à 1 la valeur de la vitesse limite » c » ( choix d’unités « ad hoc » ), alors la vitesse limite sera illustrée par la bissectrice de OX et OT, à 45 degrés de chacun, donc . ( Dans le cas Minkowskien complet XYZT, on appelle cette notion le « cône de lumière », je crois …) Les trajectoires issues de O et admissibles sont au dessus de la bissectrice ( vitesse inférieure à la vitesse limite ) . Prudemment, je n’évoque pas la partie gauche de la figure ( en principe, ce devrait être symétrique, mais bon faisons simple …) . Sur cette même figure, comment peut-on alors illustrer les nouveaux axes de coords OX’ et OT’ ? Ils ne sont pas obtenus par une rotation mais par une transformation de Lorentz (2D), chacun des nouveaux axes OX’ et OT’ sera « incliné » par rapport à l’ancien axe correspondant ET ( point important!) leur bissectrice sera LA MÊME que pour les anciens axes de coords . Pourquoi la même ? Parce la vitesse limite est la même pour les deux « référentiels », autrement dit l’équation de cette bissectrice commune aux deux systèmes de coordonnées est la même dans les deux systèmes, soit X = T et pareillement X’ = T’ . On peut donc illustrer OX’ et OT’ symétriques par rapport à la bissectrice commune et ils ne sont pas orthogonaux ( angle inf ou sup à 90 degré, et attention aussi au fait que les échelles VISUELLES sur les axes anciens d’une part et nouveaux d’autre part sont affectées et seront différentes VISUELLEMENT ).
Pour faire la manip analogue à « faire tourner la page autour de O » pour rendre OX’ et OT’ horizontaux et verticaux, ça se complique beaucoup bien sûr . Il ne s’agit plus de faire tourner la page ici . En fait il faut envisager une déformation continue assez compliquée de la figure . Si OX’ et OT’ font initialement un angle 90 ( angle défini par les orientations positives des axes bien sûr ). Et l’analogue du cercle, globalement inchangé par la rotation ? Ici, ce doit être la courbe d’égale distance MINKOWSKIENNE à l’origine O : c’est une branche d’hyperbole située au-dessus de la bissectrice . Se peut-il que, comme pour le cas du cercle, elle soit GLOBALEMENT inchangée par la déformation continue envisagée ici ? Et ben oui, cette hyperbole est GLOBALEMENT conservée telle quelle . « Globalement » ça veut dire qu’un point donné de cette courbe se déplacera SUR LA COURBE ( initiale ) au cours de la déformation continue évoquée ici, et la courbe elle-même est inchangée ( comme pour le cercle et la rotation ….) . Mais là, je renonce à l’expliquer avec des mots …
On trouve sur internet des illustrations où ces choses sont assez bien expliquées, avec des figures statiques mais c’est quand même très éclairant . L’idéal serait une animation en continu, il y a sûrement des gens assez dégourdis pour le faire ….
A noter que l’analogie euclidien/minkowskien est aussi utile pour « illustrer » graphiquement la propriété de distance minkowskienne MAXIMALE le long d’une géodesique ( entre deux points fixes ) mais seulement en 2D (X et T) et pour une trajectoire non géodésique vraiment basique, c.a.d. un « aller » non accéléré, puis une phase accélerée « instantanée » ( demi-tour), puis un » retour » non accéléré . Soit techniquement deux segments de géodésiques non alignés successifs, mis bout à bout . On se fait d’abord les dents en illustrant/expliquant la propriété de distance euclidienne MINIMALE à l’aide de deux cercles centrés respectivement sur chacun des 2 points extrêmes ( qui se font face donc ). Quand c’est tout à fait clair, on passe au cas minkowskien 2D avec deux branches d’hyperboles dont les creux se font face, à la place des cercles . Cela peut demander quelques tatonnements mais c’est très éclairant . Cela dit ça ne remplace pas une véritable démonstration analytique valable dans le cas minkowskien « complet » ( 4 dim : XYZT ) et qui ne fait aucune hypothèse sur la nature géométrique de la trajectoire « non géodésique » .
Si ces notions vous sont familières, vous me pardonnerez la longueur de ma réponse, sinon j’espère que ce texte pourra
éventuellement éclairer quelques aspects …
ERRATUM : un des paragraphes de mon texte à été mal transmis . Désolé . Je le reproduis ici :
Pour faire la manip analogue à « faire tourner la page autour de O » pour rendre OX’ et OT’ horizontaux et verticaux, ça se complique beaucoup bien sûr . Il ne s’agit plus de faire tourner la page ici . En fait il faut envisager une déformation continue assez compliquée de la figure . Si OX’ et OT’ font initialement un angle 90 ( angle défini par les orientations positives des axes bien sûr ). Et l’analogue du cercle, globalement inchangé par la rotation ? Ici, ce doit être la courbe d’égale distance MINKOWSKIENNE à l’origine O : c’est une branche d’hyperbole située au-dessus de la bissectrice . Se peut-il que, comme pour le cas du cercle, elle soit GLOBALEMENT inchangée par la déformation continue envisagée ici ? Et ben oui, cette hyperbole est GLOBALEMENT conservée telle quelle . « Globalement » ça veut dire qu’un point donné de cette courbe se déplacera SUR LA COURBE ( initiale ) au cours de la déformation continue évoquée ici, et la courbe elle-même est inchangée ( comme pour le cercle et la rotation ….) . Mais là, je renonce à l’expliquer avec des mots …
Pour Vincensini : Je ne parviens pas à transmettre mon texte correctement , je ne sais pas pourquoi . Je l’ai rédigé avec soin et tenais à vous le transmettre Je n’ai pas d’autre moyen que de le poster sur un blog . Désolé .
http://tarentedusoir.over-blog.com/2020/04/reponse-a-vincensini.html
Sérieusement ? La simultanéité change de plusieurs années quand le vaisseau fait juste demi-tour ?… Je n’avais pas compris ce point dans la théorie, c’est encore plus grave que je pensais… Il n’y en a pas un qui se dit qu’il y a un problème grave là ? Là je comprends pas comment un physicien peut accepter un truc pareil…
Pourtant la simultanéité c’est tout simple, on peut facilement la définir strictement par une expérience de pensée : deux événements se produisent « en même temps » dans l’univers quand un observateur pouvant se déplacer instantanément (à une vitesse infinie) voit ces deux événements au même moment, et voilà, pas la peine de chercher à emberlificoter des trucs super basics… Après on s’étonne que les gens se détournent de la physique.
Justement, être à deux endroits différents à un même moment est impossible, ce ne peut pas être à la base d’une notion physique (la simultanéité). J’imagine en m’amusant un univers peuplé de moi, partout.
Une expérience de pensée est une « proposition d’expérience » en quelque sorte, qui devrait pouvoir être physiquement mise en œuvre. Et se déplacer ou plus généralement transmettre une information plus vite que la vitesse c de la relativité n’est pas possible dans le cadre de la Relativité – qui a été créé pour expliquer le résultat imprévu de l’expérience de Michelson-Morley au départ.
Donc cet observateur n’existe pas dans ce cadre.
Et pour des raisons « historiques » la vitesse limite c de l’information a été d’abord la vitesse de la lumière dans le vide.
Quant aux solutions simples : A chaque question subtile et complexe, il existe une réponse parfaitement simple et directe,
… qui est fausse. (H.L. Mencken)
Pour rappel le résultat de l’expérience de Michelson-Morley est parfaitement normal si on applique la composition des vitesses aux ondes électromagnétiques (avec le mouvement de la Terre donc dans ce cas), on a pas du tout besoin de la relativité pour expliquer cette expérience.
Ah bon ?
Où trouve-t-on cette explication non relativiste de cette expérience ?
Le problème posé par l’expérience de Michelson-Morley est souvent mal compris car on ne se rappelle plus du contexte de l’époque et pourquoi elle a été réalisé :
Les scientifiques avaient déjà bien constaté que les ondes électromagnétiques sembaient ne pas obéir à la composition des vitesses et se déplaçaient partout où elles pouvaient être observées à la vitesse de c exactement… Du coup ils pensaient que dans le sens du mouvement de la terre autour du soleil les rayons lumineux se déplaçaient à c sans compositions de vitesses, et dans ce cas en les faisant interférer avec des ondes se déplaçant perpendiculairement, on aurait dû observer un changement des franges d’interférence en tournant le dispositif entier. Ce qui ne fut pas le cas.
Mais bien sur si les ondes obéissent à la composition des vitesses l’expérience devient complètement triviale, j’avais fait la démonstration mathématique avec cette hypothèse quand j’étais jeune et beau et j’étais tombé sur un résultat du genre 1=1… Pour l’anecdote j’avais envoyé ce résultat à l’académie des sciences, et le type m’avait répondu gentiment qu’on savait que la relativité restreinte n’était pas parfaite mais que pour le moment c’était ce qu’on avait de mieux 🙂
Dont acte. A l’époque je crois que je n’avais pas encore compris que les ondes électromagnétiques sont EMISE par tout ce qui les produit (que ce soit création complète ou « transmission ») à la vitesse de c exactement.
C’est vraiment la présentation la plus complète que j’ai vu/lu sur ce paradoxe. En particulier la partie sur les simultanéité relatives et l’effet de l’accélération et du demi-tour est passionnante (et condensée).
Et l’exposé qui suit montre bien que la relativité restreinte traite aussi des corps en accélération.
A propos de cet exposé, ce principe de Mach sur la distribution de matière de l’univers ne permet-il pas aussi de définir le temps cosmique ? Sur le temps cosmique, l’article de Wikipédia est assez clair : En cosmologie, le temps cosmique est le temps propre d’un observateur dit « fondamental » ou « comobile » appartenant à un univers homogène et isotrope. En pratique, l’univers n’est pas exactement homogène et isotrope, mais en moyennant la distribution de matière de l’univers, on peut considérer qu’il l’est et ainsi utiliser le principe cosmologique. Le temps cosmique est alors le temps propre d’un observateur au repos par rapport à cette distribution de matière moyenne : c’est le temps de son référentiel comobile qui est le même pour tous les référentiels comobiles puisque l’univers est homogène et isotrope. Cette situation, permise par le principe cosmologique, est exceptionnelle en relativité générale (fondement théorique de la cosmologie), car normalement il n’y existe pas de temps universel absolu, mais un temps qui est propre à chaque observateur et sa ligne d’univers.
On a l’impression que le temps absolu de Newton sorti par la porte est revenu par la fenêtre grâce à la notion de temps cosmique. Mais par rapport au temps absolu, ce temps cosmique est « expérimental » : nous pouvons vérifier si nous sommes dans un tel référentiel inertiel par exemple en vérifiant que nous somme (à peu près) immobiles par rapport au fond cosmologique.
Le principe de Mach est à la base d’expériences de pensées qui ont influencé fortement les réflexions d’Einstein.
Bonjour à tous
Bon ben je dois avouer que je n’ai pas compris grand chose, je n’ai pas de formation en mathématiques ni en physique aussi pointu que les votres, je fais partie du commun des mortels, mais lire ces articles m’ont ouvert l’esprit, merci à vous,
Grand respect
Christian
Bonjour David et bonjour à tous,
Tout d’abord merci pour cette vidéo et ce billet, comme bien souvent, très intéressants. D’autant plus que ce paradoxe des jumeaux fait naître beaucoup de questions.
Avant d’indiquer quelles sont les miennes, je précise que je suis novice en physique et mathématiques. Il y a donc sans doute certaines choses que je n’ai pas comprises.
Dans ce paradoxe, on indique qu’au terme du voyage les jumeaux n’ont pas le même âge, tant bien d’un point de vue « mathématiques » (mes excuses pour cet emploi très approximatif) que biologique (sous-entendu leur apparence physique). Très bien.
Je peux comprendre que sur le plan « mathématiques » ils n’aient pas tous les deux le même âge. En revanche, j’ai plus de mal à le comprendre sur le plan biologique. Si j’ai bien compris le paradoxe, sur un plan biologique cela signifie que les cellules du jumeau parti pour Proxima du Centaure vieillissent plus lentement que celles de celui resté sur Terre.
C’est là que je m’interroge. Qu’en est-il de notre chronobiologie dans ce cas-là? Cela signifie-t-il qu’elle aussi est touchée par les effets du voyage? Notre horloge biologique n’est-elle pas elle-même le référentiel de notre organisme? Autrement dit, ne serait-ce pas plutôt elle qui traduit notre vieillissement cellulaire plutôt que le référentiel dans lequel se trouve notre organisme? Pourquoi notre biologie serait-elle impactée par les effets du voyage?
Je précise ma réflexion. Le jumeau resté sur Terre vieillit donc de 12 ans biologiquement alors que le jumeau voyageur aurait vieillit de seulement 9 ans, soit la durée écoulée dans son temps propre. Pourquoi ne pourrait-on pas dire que le jumeau qui a voyagé a subi un vieillissement de 12 ans (temps biologique) en seulement 9 ans de temps propre? Si c’était le cas lors de son retour sur Terre, le jumeau voyageur aurait effectivement perçu la durée écoulée comme étant 9 ans mais son organisme, lui, aurait tout de même subi un vieillissement de 12 ans. Les jumeaux n’auraient effectivement pas vécu le même temps propre durant ce laps de temps mais leur organisme aurait pour chacun d’entre eux vieilli de 12 ans. Par conséquent, la différence d’apparence physique liée au vieillissement ne devrait pas être visible. Physiquement l’un et l’autre auraient tous deux subi un vieillissement de 12 ans. Aucun des deux ne devrait paraître plus vieux que l’autre.
Si je m’en tiens à ma compréhension de ce paradoxe, un changement de référentiel (couplé à une très grande accélération) impacterait la perception de notre temps propre mais aussi celle de la durée de nos processus biologiques.
Merci par avance des différents retours.
Bonjour, et merci pour cette vidéo très claire. Vous insistez surtout sur ce qui se passe quand la fusée fait demi-tour (changement de référentiel inertiel, ou accélération si on préfère analyser l’expérience en ces termes). Mais il me semble qu’il faudrait aussi prendre en compte ce qui se passe au début et à la fin du voyage : le voyageur subit aussi une accélération quand la fusée décolle, puis une décélération pour revenir sur terre. Du coup, la différence d’âge réellement observée ne sera t-elle pas plus grande (d’un facteur 2 ?) que celle que vous calculez dans la vidéo ?
Bonjour à tous,
Merci pour cette superbe explication qui m’aura bien éclairé, mais pas à la vitesse de la lumière. En fait j’ai une question purement technique, j’ai fait pause sur les équations, et je n’arrive pas à comprendre comment le terme c peut sortir lorsque les nombres sont mis dans l’équation. Merci pour vos réponses
Aurélien
Bonjour,
L’analyse du « paradoxe des jumeaux » avec la relativité restreinte est très intéressante, sauf qu’il est absolument certain qu’il faut changer de représentation de l’espace-temps, et, à partir de là, la compréhension de ce « paradoxe » va être différente.
En lisant l’article en référence (« De l’impossibilité théorique à ce que la vitesse de la lumière soit invariante dans tous les cas de figure ») on comprendra pourquoi il faut changer de représentation de l’espace-temps:
http://www.leprincipemoteurdelunivers.com/pages/projet-d-article-pour-revue-scientifique-a-comite-de-lecture.html
Dans cet article il manque l’annexe mathématique, je suis prêt à rémunérer ce travail:
http://www.forum2.math.ulg.ac.be/viewthread.html?SESSID=0545ba95aae79d077dc5f5be818358be&id=13319
Bien cordialement
Philippe de Bellescize
J’ai une question : au sujet du paradoxe des jumeaux, si jamais l’univers est un espace multi-connexe (ce qui est plutot crédible en vu des différentes topologies cosmiques envisageables), il n’y aurai pas de brisure de symétrie puisque le jumeau en voyage dans l’espace pourrait rejoindre son frère sans jamais faire de demi-tour, comment résoudre le paradoxe a ce moment la ?
Je me demande si la réponse à la question d’Hugo ne se trouve pas au moins en partie dans la question que j’ai posée un peu plus haut : ne faut-il pas aussi tenir compte de l’accélération au décollage et de la décélération à l’atterrissage ?
Salut David,
Superbe post et vidéo.
J’ai fait des études scientifiques mais je n’ai jamais vu cette partie de la physique dans mes études.
Je n’ai pas bien compris pourquoi la différence de temps viendrait du changement de vitesse au retour du jumeau voyageur.
Je me rappelle avoir lu je ne sais où que c’était la concentration en énergie par volume d’espace qui permettait de calculer la courbure de l’espace temps.
Et que c’était cette courbure qui provoquait les effets relativistes sur une trajectoire rectiligne.
En effet, pour atteindre une vitesse, il faut accélérer et donc accumuler de l’énergie (cinétique), ce qui augmente la concentration en énergie du corps en mouvement et donc la forme de l’espace autour de lui durant son voyage jusqu’à décélération.
Du coup, la différence d’âge viendrait non pas du retour mais serait une accumulation d’un biais introduit par la courbure dés le départ, du fait que le jumeau a voyagé avec une certaine énergie (cinétique), capturée lors de l’accélération initiale et restituée lors de la décélération (ce qui explique pourquoi le jumeau voyageur, une fois immobile, vieilli de nouveau « normalement » pour un observateur immobile à Proxima).
Chose qu’on pourrait observer en imaginant que le jumeau terrestre décide de rejoindre son frère sur Proxima mais avec une vitesse différente (donc une énergie différente et donc une contraction de l’espace durant le voyage différente).
Est-ce que j’ai bien compris?
Merci pour cette vidéo !
Si je comprends bien, pour un photon, un corps qui se trouve sur sa géodésique ne peut avoir que deux âges apparents : l’âge qu’il avait lorsque le photon y est passé, ou bien l’âge qu’il aura lorsque le photonl y passera. Mais si le photon se trouve sur une orbite circulaire (à la « surface » d’un trou noir), on est dans les deux cas à la fois, comment trancher ?
Pour les corps qui ne se trouvent pas sur la géodésique du photon, l’âge apparent doit se situer entre les deux extrêmes, mais lequel ?
Sinon, rien à voir avec les questions précédentes, mais je butte sur le principe de Mach depuis que j’ai appris à l’école qu’il existe un référentiel « absolu » pour les rotations. J’aimerais savoir si la solution de ce « paradoxe » est formalisée, ou s’il s’agit plutôt d’une sorte de consensus entre physiciens. Si il y a une vraie solution, j’aimerais bien savoir où chercher davantage d’infos sur ce sujet.
Je me réponds à moi-même : non, il n’y a pas que deux âges apparents, je suis juste pas encore assez à l’aise avec le diagramme de Minkowski 🙂
En revanche, pour le principe de Mach, ma question reste entière.
Bonjour, il y a quelque chose que je ne comprends pas : je croyais (naïvement sans doute) que la vitesse de la lumière dans la vide était constante quelque soit le référentiel considéré. Or, dans la vidéo, David nous dit que la lumière, du point de vue des photons, met environ 6 mois à atteindre proxima du centaure alors que du point de vue de l’observateur terreste elle met un peu plus de 4 ans (puisque proxima du centaure est à environ 4.2 années lumières du soleil)
Du coup, j’y comprends plus rien …
Quelq’un saurait m’expliquer ?
Le photon a son temps propre. Dans son temps propre, il ne met que 6 mois pour rejoindre proxima. Pour un observateur avec un autre référentiel de temps, celui de la terre, il met 4,2 ans.
Bonjour,
Tout ce qui est dit dans cette vidéo est exact. Cependant je voudrais attirer votre attention sur le point suivant : la notion de jeunesse et de vieillesse. Dans cette expérience de pensée, il est dit, que le jumeau qui a quitté la Terre est, à son retour, plus jeune que son frère. C’est exact sur le plan temporel mais son corps aura prématurément bien plus vieilli que celui de son frère resté sur Terre. Nous n’affrontons pas impunément les contraintes d’un temps propre ralenti. Les dégradations physiologiques des occupant de l’ISS, en apportent la preuve.
Je voudrais aussi dire que la géométrie des référentiels doit être prise en compte. Ce n’est pas seulement un espace limité par les grilles orthonormées que l’on voit souvent représentées dans un cube, mais par des grilles enroulées et entraînées par la masse des corps célestes (planètes, étoiles, galaxies, trous noirs, amas de galaxies…). Ceci dans le cadre de l’Univers. Nous avons les mêmes configurations à l’échelle subatomique. Si cela vous intéresse voici le site : http://www.universstrobofractal.fr
Ce que vous dites est très intéressant. J’ai eu la même réflexion : Et si tout était lié ? Si « impression », « fatigue », « stress », « usure de la vie » n’étaient pas indépendant de ce que nous avons identifié comme grandeurs physique ?
Je ne dirais pas que le jumeau voyageur souffrirait des « contraintes d’un temps propre ralenti »: concernant purement la grandeur physique du temps, il ne se passe rien de spécial dans ce vaisseau. David Louapre le souligne je crois : On ne peut pas dire que « le temps ralentit ». Le temps s’écoule normalement, pour celui qui est dans le vaisseau.
Cependant, là où je vous rejoint, c’est que celui qui veut faire un bond dans le futur doit se taper un sacré voyage ! Déjà, en restant sur terre, nous avons tous expérimenté des années qui nous « usent » plus que d’autres. Même en restant sur terre un jumeau peut décéder plus vite que l’autre. On peut se demander aussi : A quoi cela sert-il de passer 4 ans coupé du monde dans un vaisseau, pour « gagner » 2 ans ? A l’arrivée, soyez en sur : Vous auriez surtout l’impression d’avoir perdu 4 ans !! 🙂
On pourrait argumenter, qu’en moyenne, les voyageurs mourraient 2 ans plus tard une fois revenus sur terre, puisque ayant vécu 2 ans de moins ? En théorie, et en se limitant aux hypothèses simplifiées d’un cas, peut-être. Mais personnellement, je ne parierai pas forcément sur le gars resté 4 ans enfermé, alimenté en intraveineuse à boire son urine, par rapport à celui ayant passé 6 ans à manger des légumes frais avec une activité sportive régulière …
Je me souviens du moment où j’ai réalisé, étant enfant, qu’une après-midi à s’amuser passait plus vite que si je m’ennuyais. Cela correspond, évidement, à l’age où j’ai appris à lire l’heure. Je pensais donc le temps absolu : C’est moi qui me trompais, et l’horloge prouvait mon erreur. Mais, tous comptes fait (et c’est là le plus dur : prendre tout en compte), tous comptes fait, dans mon référentiel: une après-midi m’avait parut plus courte, et n’est-ce pas là l’essentiel ? Le temps a-t-il une importance, autrement que pour un être pensant ? Et si l’être pensant considère que le temps est vite passé, en quoi un mécanisme sans vie pourrait le contredire ? Ces raisonnements sur le vieillissement n’ont de sens qu’appliqué à des êtres pensants. Tant que c’est une horloge qui rentre sur terre en indiquant 2 ans de moins, ça n’a rien d’émouvant. On peut presque dire que rien ne s’est passé en fait. Les horloges que nous avons fabriqué collent avec les équations que nous avons fabriqué. D’ailleurs, l’énoncé de Langevin prend des jumeaux, pas des horloges.
Attention, je ne dénigre pas les horloges 🙂 …elles servent à se coordonner. Elles servent à ce que celui qui n’a pas vu passer son après-midi puisse retrouver à 19h pour l’apéro, celui qui s’est fait ch..r toute l’après-midi. Notre calcul du temps permet aux jumeaux de se retrouver en prévoyant que celui qui reste sur terre revienne dans 6 ans au même endroit, et impose à l’autre de voyager à une certaine vitesse durant un certain temps, avant de faire demi-tour et revenir à une vitesse définie. Si nos calculs sont exacts, alors celui qui a passé dans un vaisseau 4 ans lui semblant une éternité, retrouvera exactement au même endroit, celui qui s’est marié, a eu 3 enfants, a fait construire une maison, et n’a pas vu les 6 ans passer.
Bonjour,
Pour ce qui est du vieillissement des astronautes, je me fie aux études faites à ce sujet sur l’état de santé des occupant de l’ISS dont la vitesse n’est (heureusement) égale qu’à 0,000025 fois celle de la vitesse de la lumière, mais malheureusement dans le mauvais sens de rotation (Ouest->Est). Alors oui, il y a l’état d’apesanteur qui joue mais pas seulement. Quand vous êtes dans l’ISS vous faite corps avec celui-ci au même titre que les boulons et les tôles qui le compose. Sur mon site*, je donne les résultats d’une étude sur ce sujet : La densité des minéraux dans les os baisse (20% de perte osseuse en 6 mois). Les artères vieillissent (de 20 à 30 ans en 6 mois ! …). Malgré les exercices physiques imposés, les muscles s’atrophient. Les proportions de graisse augmentent et le système immunitaire se dérègle.
*http://www.universstrobofractal.fr
Merci pour cette vidéo très pédagogique et bravo pour parvenir à être synthétique sans être approximatif!
Pour ma part, l’explication que je m’étais donnée pour l’inversion de la ligne de simultanéité est la suivante :
1) Quand je vois une étoile, je la vois telle qu’elle était au moment où elle a émis la lumière qui me parvient (cas de 1ère ligne de simultanéité qui me fait « voir dans le passé » de l’étoile, alors que je continue de m’éloigner d’elle). Plus je m’éloigne d’elle, plus les images qui me parviennent d’elle me parviennent avec un léger « retard ». Je la vois en quelques sorte « au ralenti ».
2) Si je décide cette fois de me diriger vers l’étoile, au fur et à mesure que je me rapproche d’elle, je vais donc voir en « accéléré » tout ce qui s’y est passé entre l’époque vue en 1) et celle où je l’aurais rejointe.
C’est en effet cette construction mentale, qui, pour ma part, me permet de justifier l’inversion de pente à l’origine du « paradoxe ».
Je pense que le concept de l’expansion de l’univers offre pas mal d’exemple d’application…
Salut. Merci pour tes vidéos que je regarde assiduement.
J’ai une question qui est amusante : Si A reste sur terre et que B part dans un vaisseau à une vitesse proche de la lumière, puisqu’il n’y a pas de référentiel commun à l’univers, alors pour B, la terre part à une vitesse proche de la lumière avec A à son bord. Puisqu’il n’y a pas de référentiel absolu, pourquoi A ne serait il pas plus jeune que B à leur retour ?
C’est carrément expliqué dans la vidéo
Excuse moi, mais sur terre je subit une accélération de 1G, Comme le dit la relativité générale la gravité et l’accélération = même chose.
Donc si le vaisseau de mon jumeau part en accélérant à 1G tout le temps (sauf imaginons pendant le retournement de la fusée), et que moi sur terre pendant que la fusée se retourne, je saute (haut).
Nous avons donc subit tous les 2 exactement le même profil d’accélération. pourtant le paradoxe s’applique non ?
Pingback: Le paradoxe des jumeaux de Langevin expliqué Par Etienne Klein – Sciences Et Zététique
Pingback: Temps et relativité | Pearltrees
Bonjour,
Admettons que le jumeau « terre » envoi à chaque seconde l’information de son âge au jumeau « voyageur », cette information avançant à la vitesse de la lumière le jumeau « voyageur » connaissant sa position par rapport à la terre ne pourrait-il pas connaître l’âge de son frère à chaque instant ?
Merci de votre réponse
L’expérience de Hafele-Keating nous montre-t’elle que « la seconde » est fixe en tant que division d’un ensemble défini dans un certain système (rotation complète de la planète), mais que le temps qu’elle divise est variable, subjectif, plastique…autres termes?…
Qu’une horloge seule n’indique qu’un nombre de seconde, pas la durée de celle-ci, qui n’est pas alors absolue?
« Le temps » ne pourrait-il pas être abordé comme une densité?
Bonjour,
Merci pour cet article et cette vidéo.
Peut-on imaginer que les jumeaux communiquent de façon instantanée en utilisant l’intrication quantique ? (en mettant en place un langage codé)
Passionnant ! Toutefois vous dites que les paradoxes temporels relativistes n’ont pas de rapport avec la biologie. Mais il me semble que le temps (surtout pour un individu) est d’avantage lié à une variation d’entropie qu’à une horloge. Or il semble que l’entropie est un invariant relativiste : si c’était le cas la variation d’entropie serait la même, le jumeau stellaire vieillissant seulement « plus vite » que le jumeau terrestre… Qu’en pensez vous ?
With respect !!!
Bonjour.
Si je puis me permettre, il y a une erreur à 19:10. La flèche bleue qui apparaît à droite n’est pas l’axe de temps du nouveau référentiel, mais l’axe d’espace ! Cela fait sens car les lignes de simultanéités sont bien parallèles à celui-ci, et non à l’axe de temps.
Enfin, j’ai deux questions !
Première question -~-~-> Vous expliquez dans la vidéo que le décal’âge à l’arrivée du jumeau sur Terre n’est pas dû à une raison qui serait biologique, mais qu’il s’est simplement écoulé moins de temps. Mais le temps ne peut-il pas justement être perçu comme une notion biologique ? Typiquement, si je tape « définition seconde physique » sur Google, j’obtiens : « La seconde est la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l’état fondamental de l’atome de césium 133 ». Je ne m’y connais pas du tout en physique, mais ces phénomènes de temps relatif ne pourrait-il pas s’expliquer par le fait que la vitesse influe sur lesdites périodes de transitions ? Et donc sur tous les phénomènes biologiques en découlant.
Deuxième question -~-~-> Je ne suis pas sûr d’avoir complètement compris si cette relativité est seulement due à la vitesse.. Typiquement, si dans le futur, nous arrivons à coloniser une partie de la galaxie, dont une planète qui serait similaire à notre terre mais qui se trouverait un peu plus au centre de la Voie Lactée, les habitants de cette nouvelle planète verraient-ils le temps s’écouler différemment que nous (si on omet le décalage dû au voyage inter-planètaire) ?
Merci beaucoup pour cette vidéo !
Bonjour,
Je pars de ce questionnement :
Et si les jumeaux communiquent ?
(Edit 08/03/20) Je n’avais pas anticipé que tant de gens poseraient la question de ce qu’il se passe si les deux jumeaux communiquent « par téléphone » (ou autre) pour comparer leurs âges en permanence.
Eh bien ça ne marche pas de façon si simple, car la communication ne peut pas aller plus vite que la lumière ! Voici un schéma qui montre à quoi pourrait ressembler la conversation. Au bout d’un an dans son référentiel, le jumeau terrestre envoie un message pour donner son âge (1 an donc). L’autre le reçoit au bout de 2 ans et quelques (dans son référentiel), et décide de répondre. Le jumeau terrestre n’aura la réponse qu’à 5 ans (dans son référentiel).
L’affirmation : « la communication ne peut pas aller plus vite que la lumière » n’est-elle pas contredite par les travaux d’Alain Aspect sur l’action à distance permise par le phénomène d’intrication quantique ? Les jumeaux ne pourraient-ils pas communiquer instantanément via ce mécanisme, en supposant qu’il soit technologiquement accessible ?
Bonjour Victory,
J’ai envisagé cette hypothèse en pensant au projet d’Elon Musk d’envoyer des gens sur Mars.
Si un jumeau part et que l’autre reste sur terre, ils peuvent décider de se contacter tous les ans à date et heure fixe. Quand on sait qu’il faut environ 4 min pour la transmission d’un message vers mars on évite le problème de fusées qui s’éloigne tout en se trouvant sur deux systèmes inertiels différents.
On me dit que la réponse est connue au vu des expériences faites sur les horloges atomiques (David en parle dans sa vidéo). Mais je ne suis pas convaincu.
En mathématique le temps est une notion abstraite et on peut inverser la flèche du temps sans choquer personne mais dans la réalité physique ?
Est-ce que vraiment un des deux jumeaux vieillira moins vite que l’autre ? Grande question.
Bonjour David,
Très intéressante cette histoire de muon qui parcourt 6 km au lieu de 600 m comme sa durée de vie lui permettrait.
Interprétation A : dilatation du temps 2 microsecondes dans son référentiel équivalent à 20 microsecondes dans le nôtre. Il faut voir : A-t-on mesuré cette durée ou bien vient-elle de savants calculs de dilatation du temps pour expliquer le phénomène ?
Interprétation B : Nous détectons l’entrée dans notre référentiel d’un muon. Ce muon a une durée de vie mesurée en laboratoire de 2 microsecondes et il parcourt dans cet intervalle 6 km toujours dans notre référentiel. . Il a donc une vitesse calculée de 10 x la vitesse de la lumière….
Impossible ? Sauf si la très grande énergie dont il dispose par rapport à un électron lui donnait des propriétés particulières. Serait-ce l’exception aux lois de la relativité ?
Imaginons que l’on se serve de muons pour transmettre des informations…. N’y a-t-il pas là quelque chose d’intéressant à étudier ?
Je rêve bien sûr…