Aujourd’hui une vidéo « un petit peu spéciale », puisque je me suis rendu au CERN pour la tourner !
Je sais que la vidéo est déjà bien assez longue, mais pour ceux qui voudraient encore plus de détails, ou se poseraient quelques questions, voici un peu de compléments.
Un point tout d’abord : je suis passé assez vite sur « ce que fait » le boson de Higgs, puisque c’est un sujet que j’ai déjà traité dans une autre vidéo où j’explique notamment le lien entre le boson et la formule E=mc2.
L’histoire de la physique des particules expérimentales
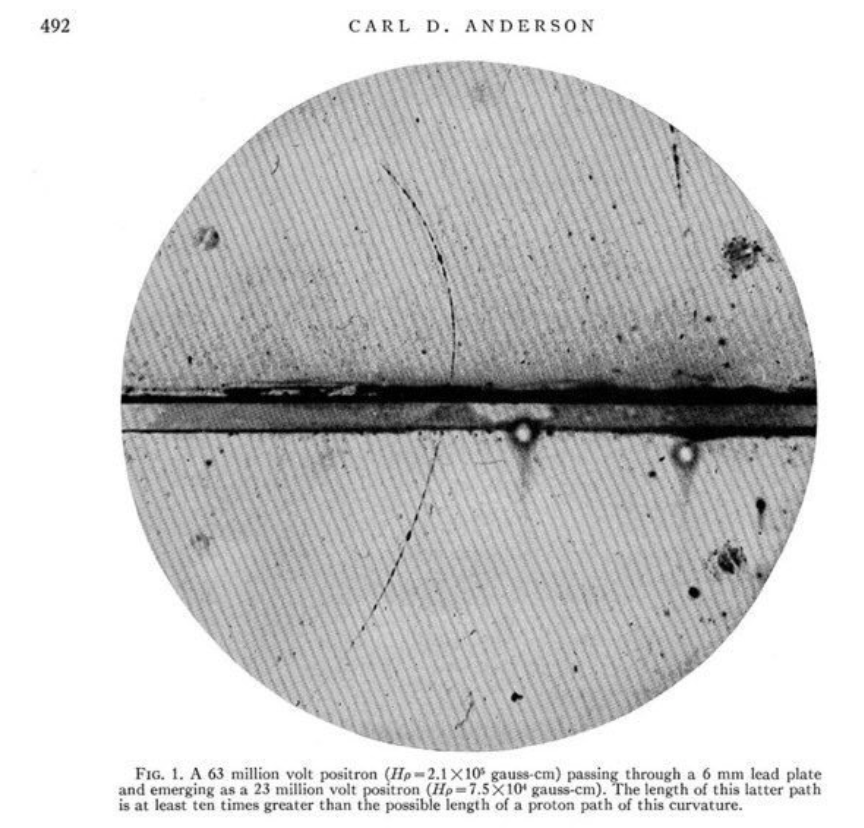
J’ai choisi de commencer mon histoire en 1932, et de me concentrer sur l’histoire de la découverte du muon en 1936. Mais la découverte de « nouvelles » particules a commencé dès 1932 avec le positron, lui aussi découvert dans les chambres à brouillard grâce à sa trajectoire dans le champ magnétique.
On peut supposer qu’il avait déjà été observé avant par d’autres qui l’avaient pris pour un proton, et c’est Anderson qui le premier l’a correctement identifié et a fait le lien avec la théorie de Dirac des électrons / anti-électrons :
Concernant l’histoire de la physique des particules expérimentales, j’ai du aller assez vite pour ne pas alourdir la vidéo, mais voici une bonne référence
Bryant, P. J. (1994). A brief history and review of accelerators.
qui présente notamment ce qu’on a coutume d’appeler Livingston plot à savoir un graphique montrant l’évolution de l’énergie des accélérateurs en fonction des années et des technologies. Je me suis créé ma propre version, mais il existe plein de façon de le faire, tapez « Livingston plot » dans votre moteur de recherche d’images préféré.
Dans l’histoire des accélérateurs, il y en a quand même un qui mérite une attention particulière, c’est le « SC », le synchro-cyclotron du CERN. Mis en service en 1957 et arrêté en 1990, ce fut le tout premier accélérateur de particules du CERN. Et c’est devant lui que je tourne cette séquence sur l’histoire des accélérateurs !
Je n’ai pas expliqué le principe du synchrotron et ce qui fait sa différence avec le cyclotron, même si une de mes animations le suggère. Dans un synchrotron, le champ électrique accélérateur est pulsé et résonnant. On ne met plus le champ magnétique sur tout un disque mais sur une couronne, et on passe d’une trajectoire en spirale à une trajectoire circulaire à rayon donné. Cela nécessite d’augmenter progressivement le champ magnétique jusqu’à sa valeur nominale et d’ajuster le champ accélérateur en fonction.
Pour créer la résonance du champ, on utilise des cavités que l’on voit schématisées sur une des animations, ce sont les deux boursouflures en forme de bouée que l’on voit ci-dessous
Vitesse et énergie
Un point vous aura peut-être surpris (ou pas), c’est le fait que la vitesse des protons dans le LHC se trouve être seulement 3 m/s inférieure à celle de la lumière. Pourquoi ne pas pousser un peu plus l’accélérateur pour atteindre la vitesse de la lumière ?
Eh bien parce qu’on ne peut pas ! A basse vitesse, l’énergie cinétique d’un corps varie comme le carré de sa vitesse. Mais quand on s’approche de la vitesse de la lumière, un autre facteur rentre en compte : les phénomènes relativistes.
Plus on s’approche de la vitesse de la lumière plus il faut fournir d’énergie pour gagner en vitesse. Si on note \(x\) la vitesse d’un corps rapporté à la vitesse de la lumière (donc \(x=v/c\)), son énergie cinétique varie proportionnellement à
\((\frac{1}{\sqrt{1-x^2}} – 1)\times mc^2 \)
Le premier terme est le préfacteur relativiste de Lorentz, qui tend vers 1 à faible vitesse mais tend vers l’infini quand on s’approche de celle de la lumière.
Du point de vue des accélérateurs, cela signifie qu’augmenter l’énergie encore et toujours n’a qu’un faible impact sur la vitesse des particules. Mais on s’en fiche, puisque c’est l’énergie qui nous intéresse !
Si vous voulez mieux comprendre tout ça, vous pouvez aller voir la vidéo de J’m’énerve pas j’explique.
La structure du LHC
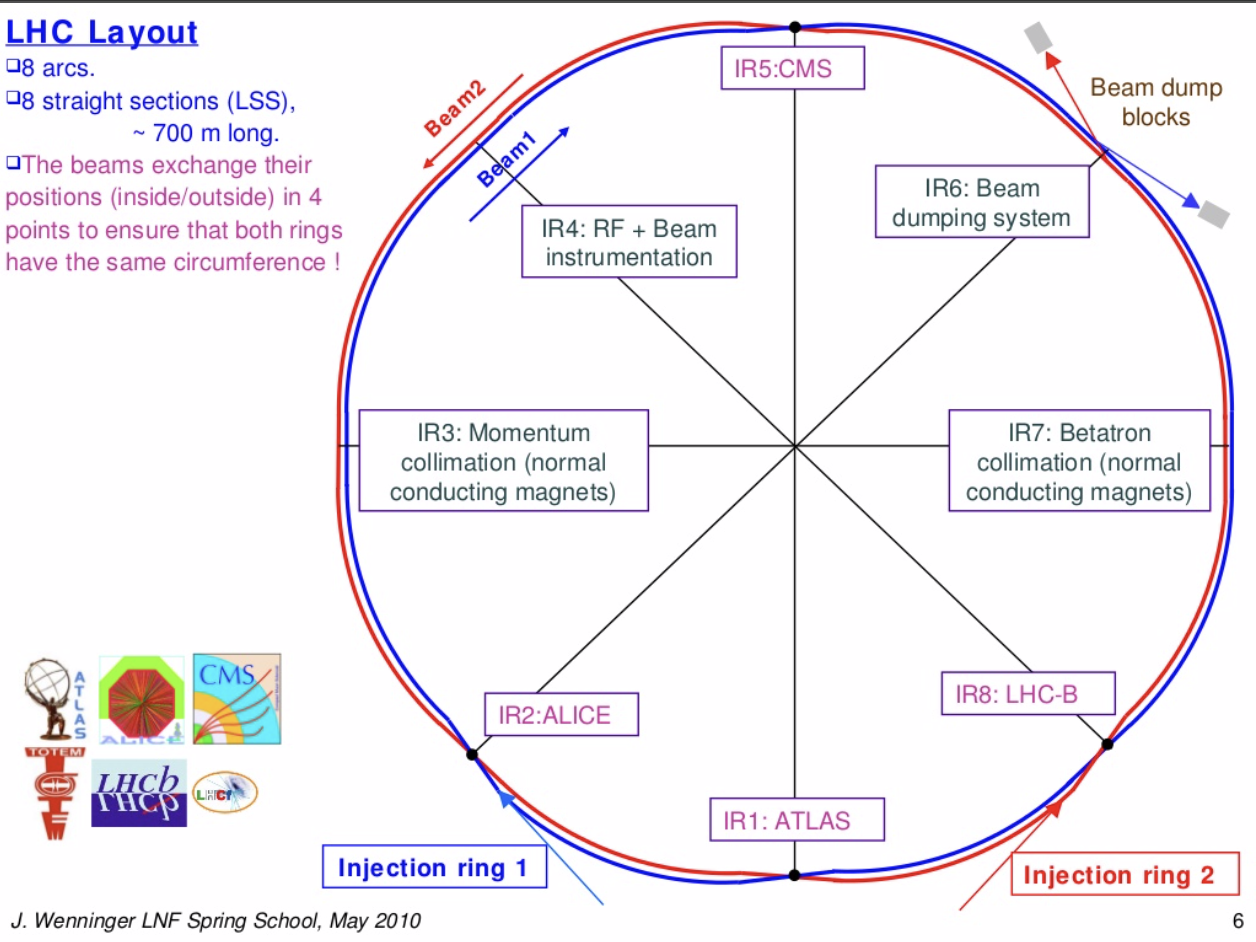
Quelques précisions concernant la structure du LHC. Je l’ai présenté évidemment comme un anneau circulaire…mais ça n’est pas tout à fait ça !
En réalité le LHC est constitué de 8 sections circulaires de presque 3 kilomètres, séparées par 8 sections droites où se trouvent les points d’injection, les cavités accélératrices et les détecteurs, ainsi que d’autres opérations.
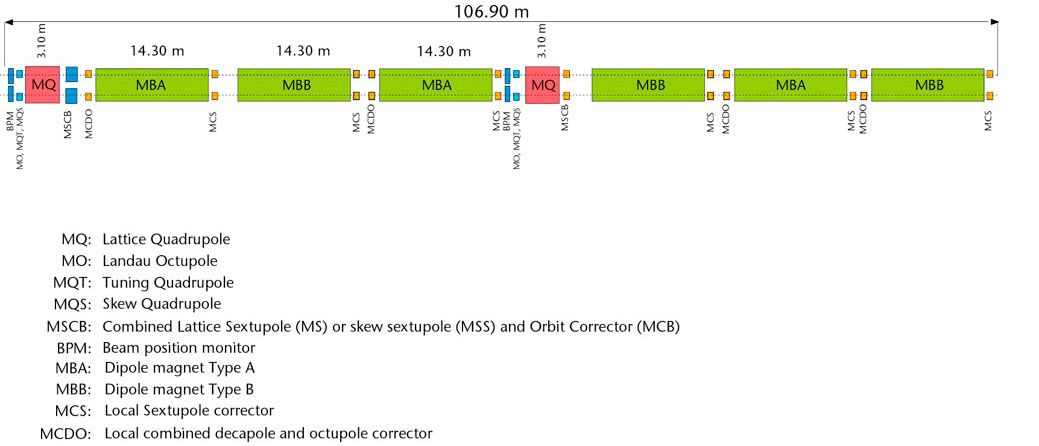
Chaque arc circulaire est divisé en cellules élémentaires dont le design est fixe :
On y retrouve majoritairement les dipôles (en vert) mais aussi les quadripôles (en rouge) qui refocalisent le faisceau, et plein d’autres petits aimants correcteurs.
Luminosité et sections efficaces
J’ai évoqué le concept de luminosité qui est une caractéristique importante des accélérateurs. Ce que l’on souhaite, c’est provoquer des collisions. Intuitivement, on sent bien que le nombre de collisions sera d’autant plus grand que le faisceau est dense (il y a beaucoup de protons par unité de volume), et que sa vitesse est élevée (car ainsi les particules se croisent plus souvent).
Si l’on multiplie la densité \(n\) d’un faisceau par sa vitesse \(v\), on obtient une grandeur dont l’unité est \(m^{-2}s^{-1}\) et dont on se dit qu’il y aura d’autant plus de collisions qu’il est élevé. Dans le cas de deux faisceaux structurés en paquets et qui se croisent, le calcul est un peu plus compliqué que ça.
La luminosité est proportionnelle au nombre de protons dans chaque paquet, au nombre de paquets, à la fréquence de croisement, et inversement proportionnelle à la surface transverse des faisceaux
\({\cal L} \propto \frac{N^2_{protons} N_{paquets} f}{S}\)
Avec un diamètre dans la zone d’interaction d’environ 15 microns, on retrouve l’ordre de grandeur de luminosité nominale du LHC
\({\cal L} = 10^{34} cm^{-2}s^{-1}\).
La luminosité permet notamment de calculer le nombre de collisions attendues, en fonction de la section efficace des interactions, c’est-à-dire en gros de la « surface de contact » des protons qui se croisent. C’est un concept un peu plus subtil que cela, mais le taux de collision (nombre de collision par secondes) s’obtient alors comme :
\(\tau = {\cal L} * \sigma_{pp}\)
Pour calculer la section efficace d’interaction, eh bien c’est compliqué ! On peut faire des estimations numériques et essayer de croiser avec les données expérimentales. J’ai pris cette source :
Total, elastic and inelastic p-p cross sections at the LHC. Tomáš Sýkora
Et surtout, cela dépend de l’énergie ! Plus l’énergie est élevée, plus la section efficace (et donc la probabilité de collision) sera forte. On voit sur le graphe ci-dessous une estimation en fonction de l’énergie (en échelle log).
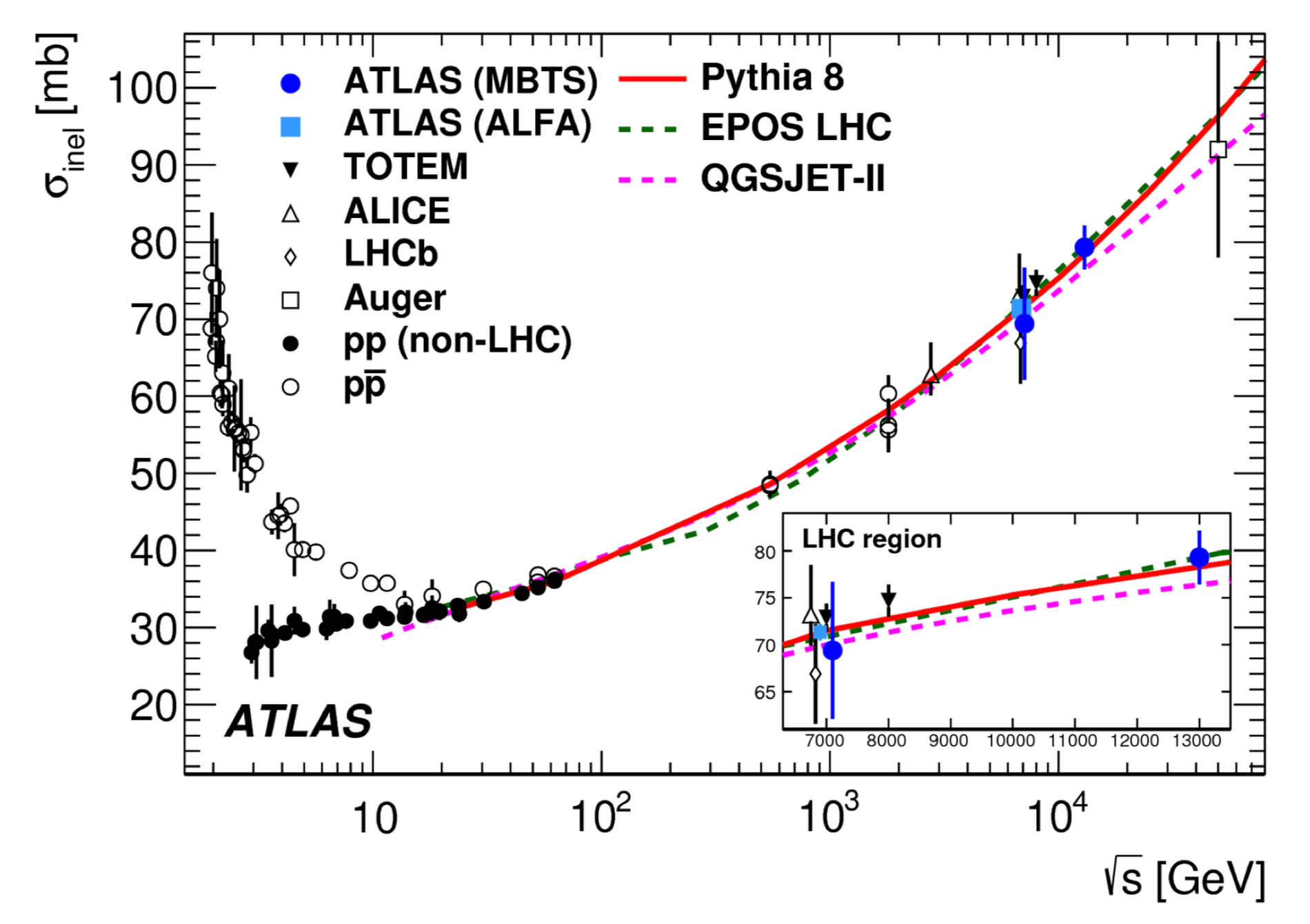Une fois que l’on connait la luminosité et la section efficace de collision, on peut estimer donc le taux de collision.
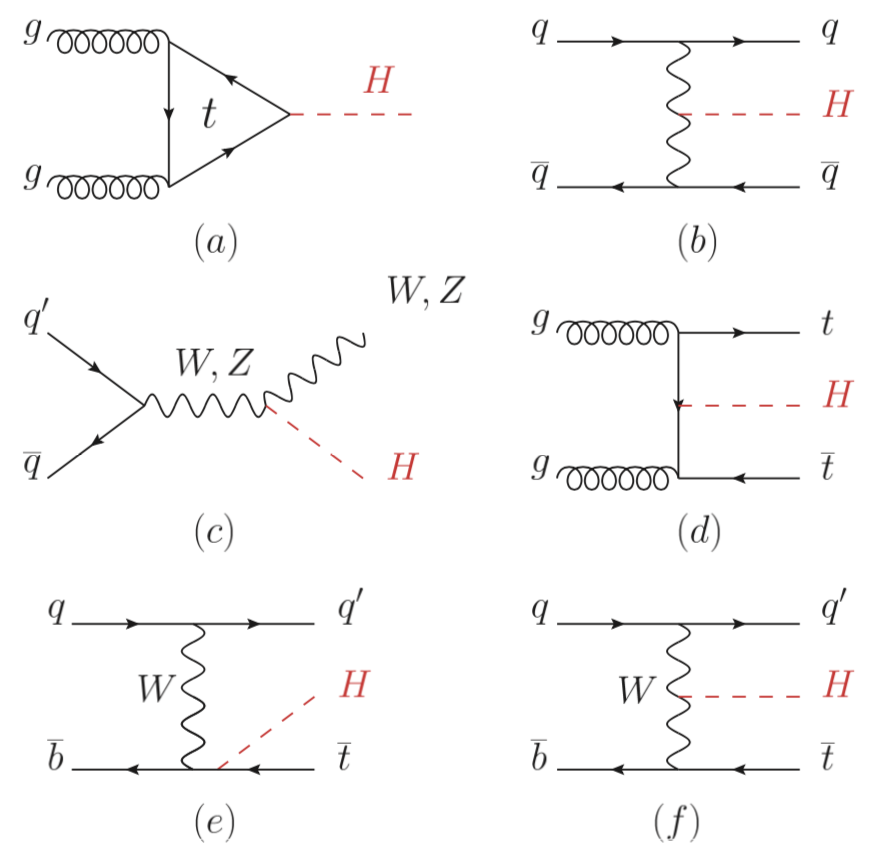
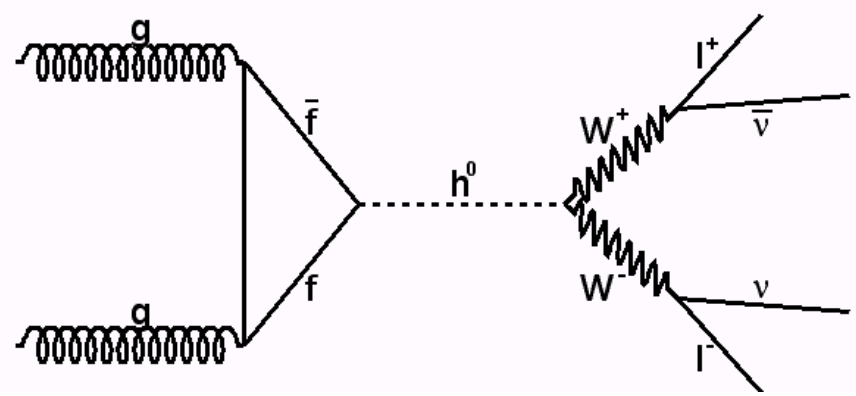
Maintenant se pose la question du pourcentage de ces collisions susceptibles de conduire à la production d’un boson de Higgs (Une bonne source : Status of Higgs boson physics) J’ai parlé du principal mécanisme, la fusion de gluons, mais il en existe d’autres moins fréquents, dont voici les diagrammes de Feynman
A chacun de ces processus correspond une section efficace, et donc une probabilité de production lors d’une collision. Les sections efficaces dépendent du processus considéré, de la masse du boson de Higgs et de l’énergie de collision,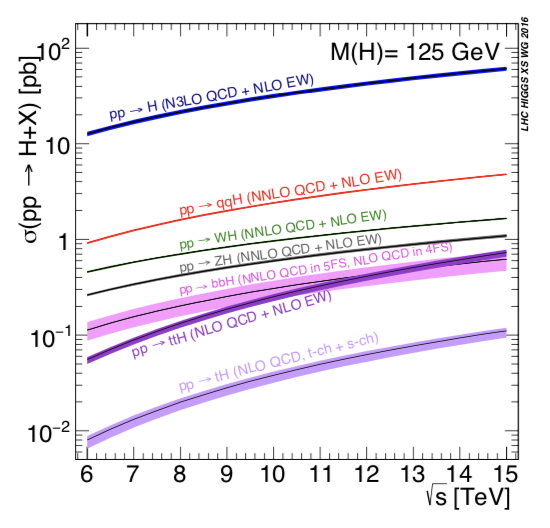
Pour les estimer, on doit avoir recours à des modèles numériques qui décrivent la façon dont interagissent les protons lors de la collision. On utilise un modèle effectif, le modèle des partons, qui permet de réaliser ces calculs suivant plusieurs niveaux d’approximations (c’est le sens des mentions NLO qui signifient Next-to-Leading Order, et on peut en ajouter pour avoir NNLO, N3LO etc.)
Modes de désintégration
Maintenant que l’on peut calculer les taux de production de Higgs, on peut s’intéresser aux modes de désintégration, et à leur abondance respective. Et là c’est encore plus compliqué car cela dépend beaucoup de la masse du Higgs.
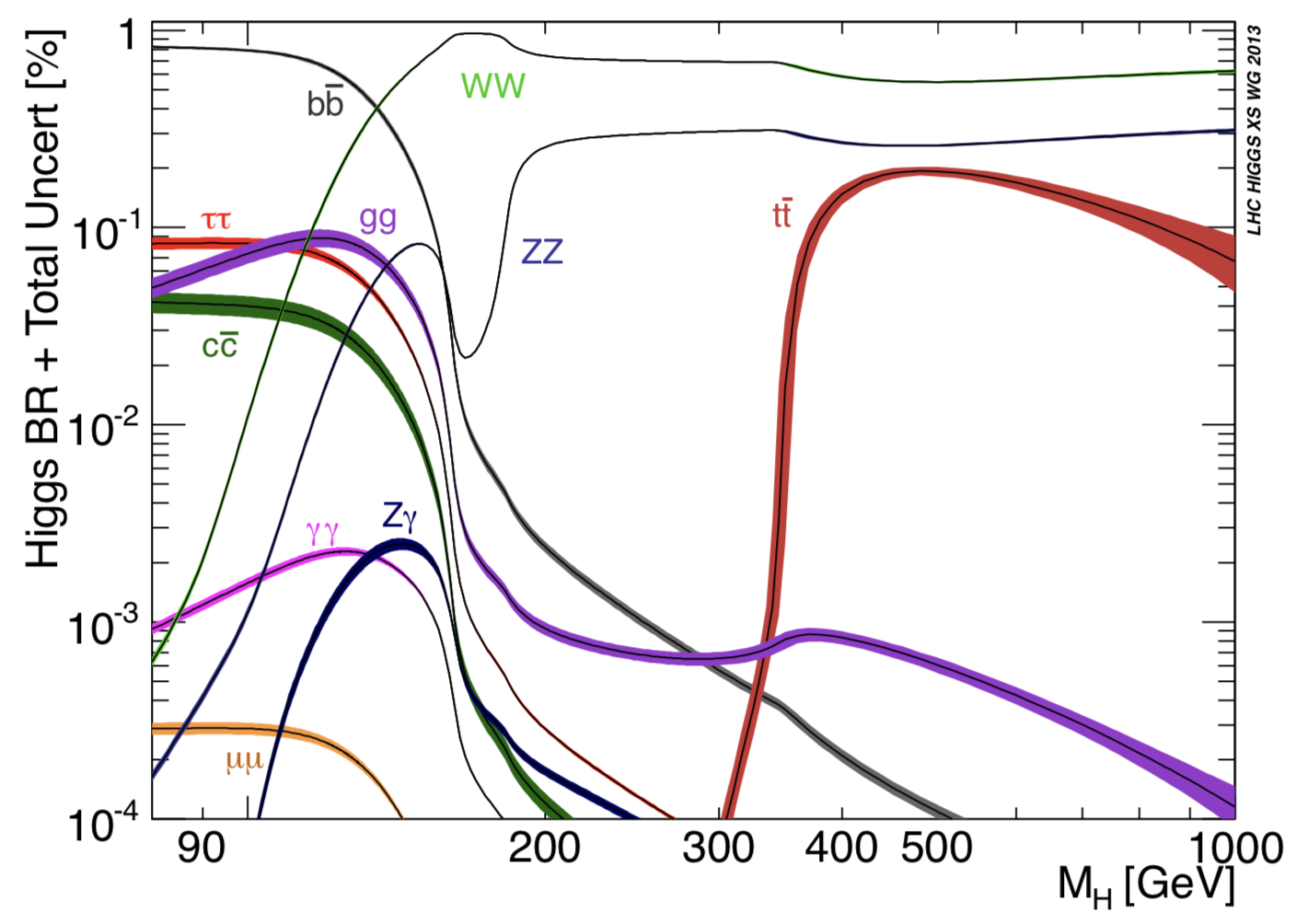
Voici le graphique qui donne la fraction de chacun des modes en fonction de la masse potentielle du boson de Higgs (source) :
Maintenant que l’on connait bien sa masse, ça parait facile, on a des ratios de façon assez précise, mais on voit qu’au moment de designer les détecteurs comme CMS ou ATLAS, il fallait pouvoir ratisser large et s’adapter aux différentes éventualités.
Voici un zoom sur la zone de masse du Higgs 110-130 GeV
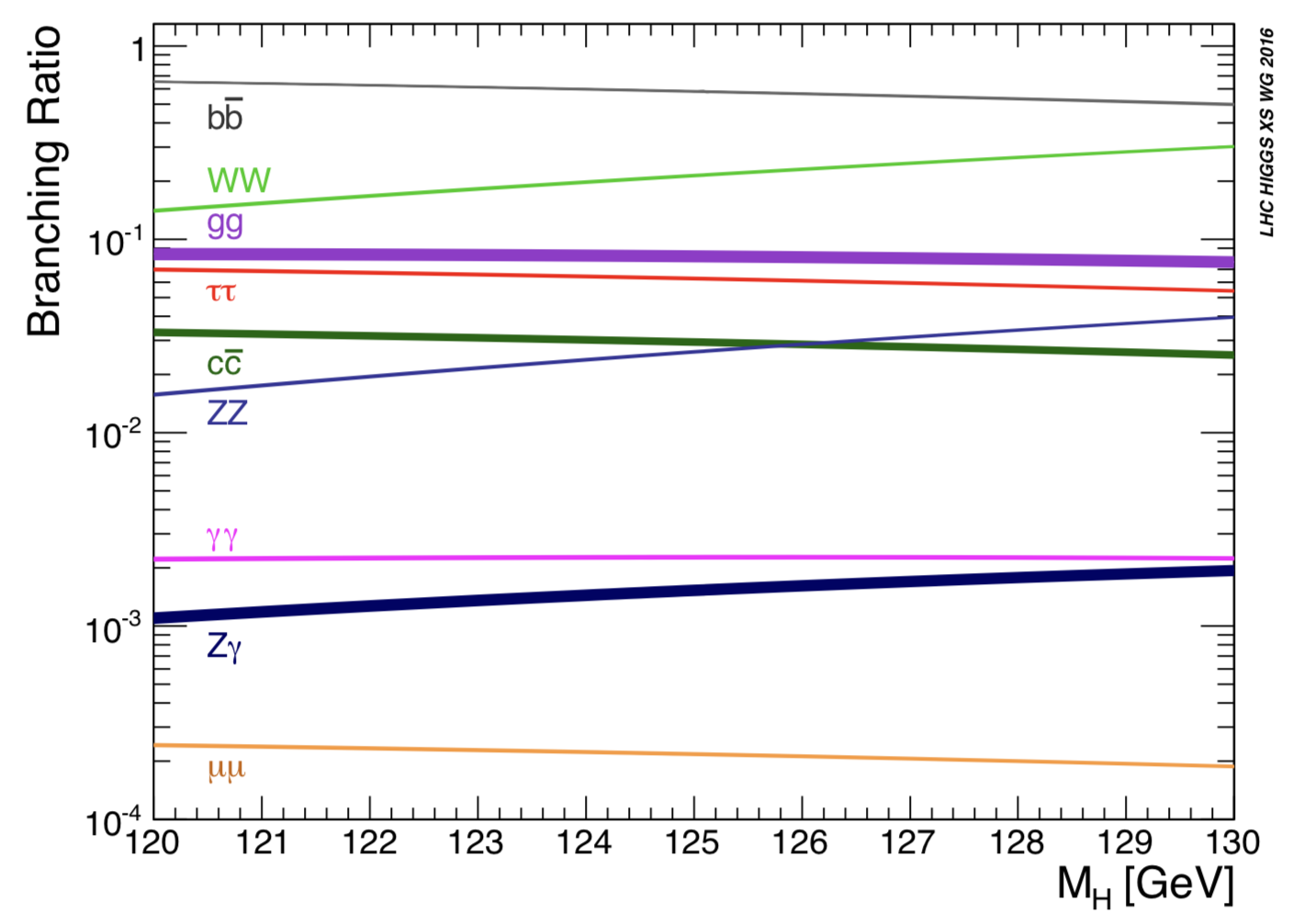On retrouve les différents canaux de désintégration dont j’ai parlé dans la vidéo (ainsi que d’autres). Comme je l’explique, tous ne se valent pas pour débusquer le Higgs. Un canal qui soit fréquent, c’est bien, mais si il conduit à une identification difficile, il ne sert à rien.
Pour cela, on privilégie les canaux ayant une signature nette, et qui permettent de reconstruire la masse du Higgs avec une bonne précision. Des canaux fréquents comme le bb où le WW ne sont pas forcément les plus utiles s’ils ne conduisent pas à une reconstruction aisée de l’énergie du Higgs.
C’est par exemple le cas du canal WW, car les deux bosons chargés vont ensuite se désintégrer en lepton avec un neutrino.
Or j’en parle dans la vidéo, les neutrinos ne sont pas détectés par les instruments comme CMS. Cela conduit à une grosse incertitude sur l’énergie mesurée, et donc à l’étalement de la bosse qui produit un mauvais rapport signal sur bruit.
Le canal à deux photons est bien pour cela, malgré un background assez abondant et donc un rapport signal sur bruit de l’ordre de 0,1.
Pour la désintégration en deux bosons Z, on voit qu’elle est relativement fréquente, 2,6% des cas, mais c’est quand chacun des bosons Z se désintègre ensuite en une paire de leptons que l’on peut vraiment avoir une bonne identification.
Il y a 3 types de leptons : électron, mu et tau. Pour chacun, la probabilité de désintégration d’un boson Z est de 3,4%. Dans un détecteur comme CMS, on ne détecte pas les taus, donc la probabilité cumulée est de 6,8%. A cela s’ajoute le fait que pour être dans le canal en or, il faut que les DEUX bosons Z se désintègrent de cette façon, donc la probabilité est de (6,8%)*(6,8%). Si on combine ça à la probabilité de la désintégration du Higgs en ZZ, on a le taux total du canal en or, environ 0,0001.
Pour connaître le nombre total de désintégrations d’un certain type auquel on s’attend, il faut donc multiplier le taux de collision par la probabilité de production d’un boson de Higgs et par la probabilité de désintégration dans le canal donné. Cela nous un taux d’événements, qu’il faut ensuite multiplier par la durée de fonctionnement.
En pratique, on commence souvent par multiplier la luminosité par le temps de fonctionnement, afin d’obtenir ce qu’on appelle la luminosité intégrée. Plus la luminosité intégrée est importante, plus les statistiques seront précises et robustes.
Combiner tout ça
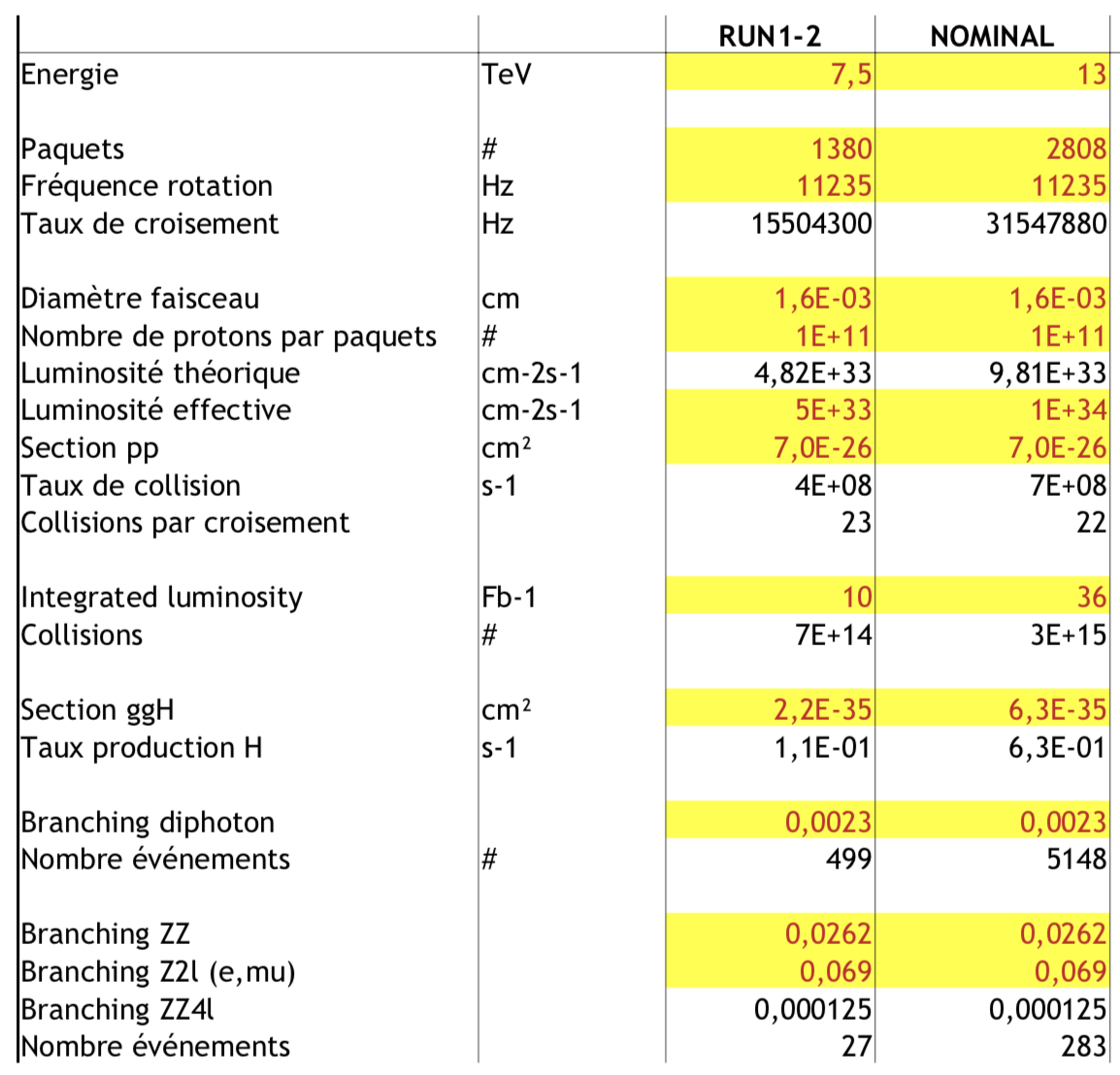
On peut s’amuser à combiner tout ça pour essayer de retrouver le nombre d’événements attendus. Cela va dépendre des caractéristiques du run (énergie, luminosité,…) et il y a en particulier une différence entre les premiers runs qui ont permis la découverte du boson, et les runs à l’énergie et à la luminosité nominale.
D’ailleurs dans ma vidéo, j’ai plutôt mentionné les valeurs nominales mais pour l’analyse des premiers runs, il faut bien sûr considérer les valeurs utilisées à l’époque.
Voici un petit tableau que je me suis fait qui résume les ordres de grandeur. En rouge sur fond jaune, les données d’entrée. Le reste ce sont des valeurs calculées à partir des données d’entrée.
Le détecteur CMS
Quelques éléments relatifs au détecteur CMS, et que je n’ai pas précisé dans la vidéo.
Je n’ai pas expliqué le principe des scintillateurs. Il s’agit de matériaux capables d’absorber certaines particules, et d’émettre de la lumière en quantité proportionnelle à l’énergie absorbée : c’est la scintillation. On place alors des photodétecteurs pour mesurer la lumière produite.
Les principes de scintillation des calorimètres électromagnétique et hadronique de CMS sont différents. Dans le cas du calorimètre électromagnétique, c’est le même matériau qui joue le rôle d’absorbeur et d’émetteur de lumière, le PbWO4.
Dans le cas du calorimètre hadronique, on utilise deux matériaux : des métaux pour absorber et un plastique scintillateur pour émettre la lumière. C’est un tel principe qui sera notamment utilisé pour le futur calorimètre électromagnétique à l’avant de CMS dans le HL-LHC.
Un mot sur la structure de l’aimant. Il est constitué en fait de deux parties : le solénoïde proprement dit, et une structure en acier qui permet le retour du champ magnétique (le terme anglais est return yoke, je ne sais pas quelle est la traduction officielle). Cela fait que bien qu’elles soient placées à l’extérieur du solénoïde, les chambres à muons sont quand mêmes bien baignées dans le champ magnétique puisqu’elles sont entrelacées avec le return yoke.
L’annonce de 2012
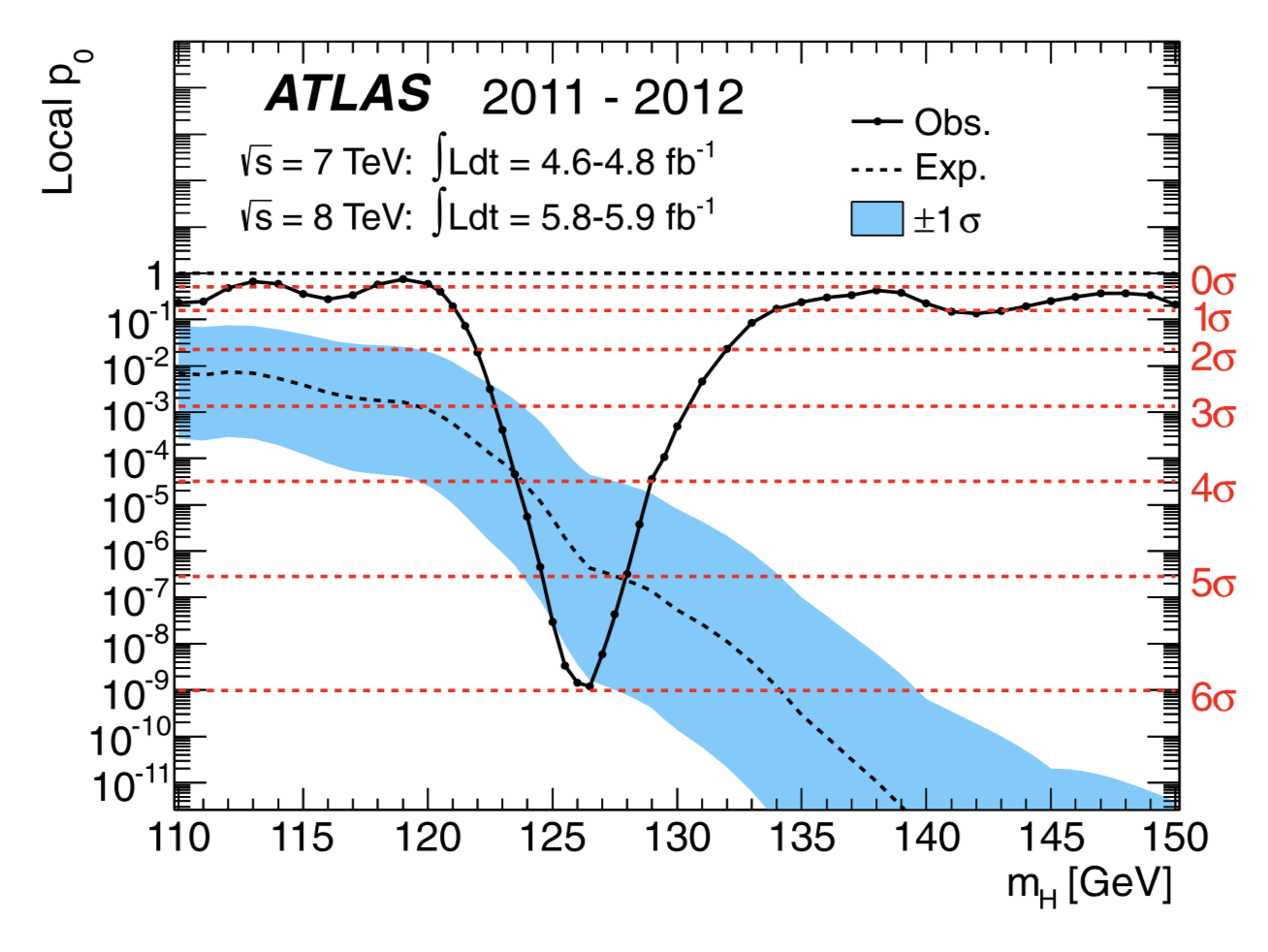
En voyant les graphiques de l’annonce de 2012, peut-être aurez-vous été surpris de voir qu’à vue de nez, les bosses dans la zone des 125GeV sont quand même bien faibles. Je précise d’ailleurs que les fits que l’on fait ne sont pas juste des lignes au jugé, mais correspondent bien au background auquel s’ajoute un signal de masse attendue.
Pour prendre en compte le cumul des observations des deux expériences dans les deux canaux, les physiciens utilisent une procédure précise, qui permet de quantifier l’équivalent d’une valeur « petit p » que l’on trouve habituellement en statistiques.
Ce graphique est tiré de la publication scientifique ATLAS faisant suite à l’annonce
Aad, Georges, et al. « Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. » Physics Letters B 716.1 (2012): 1-29.
et la publication correspondante pour CMS
Chatrchyan, Serguei, et al. « Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. » Physics Letters B 716.1 (2012): 30-61.
Taux observés vs taux attendus
Comme je l’évoque brièvement à la fin de la vidéo, on cherche notamment à s’assurer que les taux de désintégrations observées dans les différents canaux correspondent bien à ce qu’on attend d’un boson de Higgs du modèle standard.
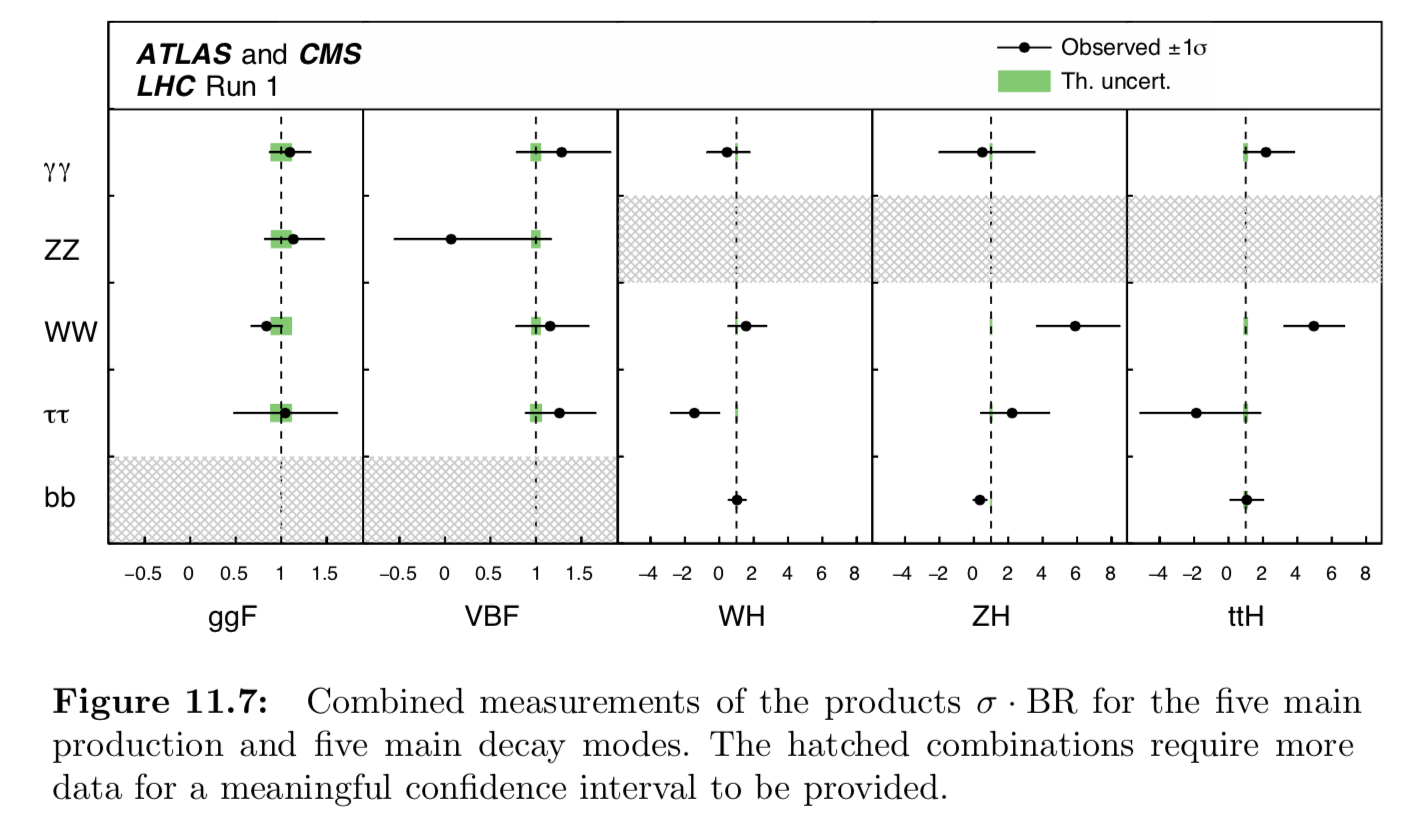
Pour cela on mesure le ratio entre les taux observés et les taux attendus, et ce pour chacun des canaux et modes de production, ce qu’on appelle la force du signal (signal strength). Pour les canaux avec un bon rapport signal sur bruit et beaucoup d’événements, on a de bonnes statistiques. Pour les autres il y a de grosses barres d’erreur.
C’est ce qu’on voit sur ce graphique (tiré de la référence que j’ai déjà cité plus haut)
27 Comments
Excellente vidéo !
Super comme d’habitude !
Cela serait tellement bien une vidéo tournée à ITER comme celle-ci, avec un focus sur les leviers technologiques qui nous empêchent de maîtriser la fusion nucléaire…
Bon en tout cas merci pour ce travail.
Merci pour cette vidéo et pour les explications !
Point de détail que je ne suis pas sûr d’avoir compris : les détecteurs sont constitués de plusieurs couches, comme un oignon. Les particules détectées dans les couches extérieures traversent donc forcement les couches intérieures ? Sont-elles « transformées » par la traversée des couches inférieures ? J’ai par exemple du mal à comprendre comment les électrons peuvent être à la fois détectés par le trajectographe et par le calorimètre. (La mesure du trajectographe ne détruit-elle pas l’électron initial ?)
Peut être un peu lié à la question précédente, j’adorerais voir une vidéo sur les « weak measurements » en physique quantique. Difficile de trouver de la vulgarisation scientifique sur ce sujet… 🙂
En effet les trajectographes détectent les particules mais en les affectant « le moins possible », donc ils ne les absorbent pas et ne mesurent pas leur énergie, et ce sont les calorimètres qui le feront.
Purée, on y est 🙂
Un immense bravo et merci, pour cette vidéo (ou ce documentaire devrais-je dire), assez différent de ce à quoi tu nous as habitué, cette fois, c’est vraiment un « c’est pas sorcier » pour les grands^^, je suis scotché.
Je vais evidemment devoir y revenir, et reprendre plusieurs fois le billet (je suis un béotien), mais c’est un plaisir ( à tel point que tes 2 livres m’attendent au pied du sapin^^)
Joyeux Noël alors!
Jerry beaucoup pour cette excellente vidéo et ce billet de blog!
Je remarque que dans la dernière figure représentant les branch ratios de la désintégration du Higgs certaines barres d’erreur expérimentales ne contiennent pas la valeur théorique. Il y a-t-il là une raison de douter du modèle standard ou est-ce que ces erreurs peuvent s’expliquer autrement?
Je ne comprend pas bien la formule que vous donnez pour l’énergie cinétique relativiste. Vous écrivez ɣmv^2/2 mais il me semble que ça devrait être (ɣ-1)m. Il y a-t-il une approximation qui m’échappe?
Ah oui bien vu ! Et c’est c au lieu de v, je vais corriger !
Et pour les branchings ratios, ça correspond à des événements très rares, donc les significativités statistiques ne doivent pas être suffisantes pour commencer à douter sérieusement.
Merci beaucoup pour cette excellente vidéo et billet de blog!
Je remarque dans la dernière figure montrant les branching ratios du Higgs que certaines des barres d’erreur expérimentales ne contiennent pas la valeur théorique. Il y a-t-il là une raison de douter du modèle standard ou sinon comment on explique ces désaccords?
Toute autre question. Je ne comprend pas bien la formule que vous donnez pour l’énergie cinétique. Vous écrivez ɣmv^2/2 mais il me semble que c’est plutôt (ɣ-1)m. Il y a-t-il une approximation qui m’échappe?
Merci pour cette vidéo, elle complète bien celle de la chaîne « J’ménerve pas, j’explique », et réciproquement:
https://www.youtube.com/watch?v=3jGy6bs7SQs
P.S.: Bon, sinon, je suis un peu déçu: on ne sait pas si les physicien(ne)s, ingénieur(e)s et chercheurs(/euses) chantent dansent toujours sur le « Large Hadron Rap », ou si ils sont passé depuis à une autre chanson 🙂
https://www.youtube.com/watch?v=j50ZssEojtM
Excellente video. C’est vraiment fascinant ce niveau de technologie deploye.
Pourrais tu faire une video ou tu expliques plus en detail les enjeux des decouvertes des nouvelles particules ? C’est le truc que je comprends pas bien. Si tous les Etats Europeens s’engagent a mettre autant d’argent dans ce projet aussi incroyable, c’est que les enjeux doivent etre monstrueux. Et quelles seraient les applications pratiques de ces decouvertes ?
Dans certains forums, ca parle de creation d’un mini trou noir, ou de trucs occultes (voir video ici https://www.youtube.com/watch?v=ijMwuZYAeA4). Un avis ?
Excellente vidéo qui, pour ma part, a clarifié un sujet qui jusqu’ici restait opaque.
Merci pour ce contenu David, continue à faire ces vidéos d’une très grande qualité et à rendre accessibles ces informations au plus grand nombre!
Salut ! Déjà un grand bravo pour cette magnifique vidéo, digne d’un documentaire ! Mais j’avais une question : dans la vidéo (je ne sais plus trop quand) tu parles des leptons en disant que ceux-ci étaient les électrons et les muons. Mais quand est-il du tau ? Voilà question, certes, plutôt débile mais je me demandais. Bonne journée à toi !
C’est intéressant cette histoire de découverte du Muon, cette « particule » un peu à l’origine de toute cette folie… J’avais déjà croisé ça une fois et comme d’habitude j’avais trouvé qu’ils avaient « déduit » son existence sur des conjectures plus que fumeuses. Je vais essayer de retrouver les conditions expérimentales précises mais c’est pas facile, c’est oublié tout ça, et les erreurs sont solidement entérinées sans plus rien remettre en question…
Ca ! ce serait des vidéos géniales de revenir sur les conditions expérimentales exactes et précises des découvertes historiques, de celle qui sont devenues les « fondements » de la « physique » d’aujourd’hui !
Je suis tout à fait d’accord avec cela.
Je trouve que David est l’un des seuls à le faire de temps en temps. Merci à Science étonnante.
La vitesse de la lumière. Il me semble que le LHC est la seule expérience qui prouve que « c » est une valeur limite supérieure, que les particules ne peuvent atteindre qu’asymptotiquement en leur fournissant une énergie infinie.
Le LHC est la preuve « ultime » en faveur de la Relativité Restreinte ? Votre avis, merci
Réponse OUI.
Si j’ai bien compris l’exposé de David, le LHC mesure la vitesse des particules avec un pas de l’ordre de 3 m/s (je trouve à 3,81 m/s avec les données : 26,659 km de circonférence, 11235 tours / s et 7000 paquets de protons).
Pour atteindre la vitesse mesurable supérieure de V= c-3 m/s, le LHC fournit au proton une énergie de 7500 Tev (ce qui correspond bien au facteur gamma à cette vitesse : 7069) . Au CERN on doit constater qu’il faut fournir beaucoup d’énergie pour passer de c-6 m/s (5000 Tev) à c-3m/s (7000 Tev)
La vitesse de la lumière est bien une « barrière » . Y a t’il un papier du CERN sur le sujet ?
réponse NON n°1.
Les particules muons créées dans la haute atmosphère prouveraient la dilatation du temps ou la contraction des longueurs, cqfd ! …
( Peut-être bien, mais je ne suis pas convaincu : en effet on ne mesure pas leur vitesse mais leur nombre résiduel à des altitudes différentes et que l’on se base sur leur demi vie pour déduire un temps dilaté ou une longueur contractée. )
Un avis ?
Réponse NON n°2
Le GPS nécessite la correction régulière des horloges atomiques embarquées dans les satellites, pour éviter les erreurs de positionnement du km apparaissant en 1 jour, cqfd !
(Vraiment ? Pour moi, si je suis bien informés, entre satellites il n’y a pas/peu de dilatation du temps puisqu’ils sont tous plus ou moins à la même vitesse et altitude. De plus le système nécessite à minima 4 satellites pour se caler : 4 équations pour 4 inconnues x, y, z et t, nos voitures ne contenant pas d’horloge atomique)
Un avis sur le sujet ?
avec les satellites, il me semble que ce qui compte c’est la dilatation avec la Terre.
Bravo pour ce toujours magnifique blog.
Mais je ne peux m’empêcher de dire que je déteste l’affreux « positron » au lieu de positon, construit comme electr-on (ou negat-on), phot-on, prot-on, etc. etc.
Encore merci
Pierre
merci pour cette belle visite du LHC,
j’ai deux commentaires/questions:
– je suis resté sur ma faim puisqu’une large partie de la présentation du LHC consiste à vanter l’énergie de collision accessible de 14 TeV. Or le boson de Higgs n’a q’une énergie de l’ordre de 125 Gev. Ce qui est déjà pas mal mais qui ne représente qu’un pour-cent seulement de l’énergie de collision annoncée au départ. Du coup, il me semble qu’il serait intéressant de rappeler l’origine de cet écart ou mieux expliquer pourquoi les physiciens ont dû développer ce nouvel instrument avec une telle énergie. J’ai ré-écouté ta vidéo E=mc² et le boson de Higgs pour tenter de trouver une réponse à cette question qui a dû en tarauder plus d’un mais ce n’est toujours pas évident pour moi…
En effet, on pourrait se dire qu’avec le LEP des années 90 par exemple, cette découverte aurait déjà pu être faite, moyennant les bons détecteurs nécessaires à cette détection. Finalement, comme les physiciens ont-ils justifié devoir développer un LHC avec une énergie de 14 TeV? Est-ce parce que la masse présumée du boson de Higgs balayait une plage tellement large qu’il fallait dépasser le 1 TeV absolument? ou n’ai-je pas compris un truc évident qui n’est pas explicité dans ta vidéo et ton billet?
– Enfin, concernant les taux de désintégration des différents canaux: tu dis dans la vidéo que les observations collent parfaitement avec les prédictions. Dans le billet, tu es un peu plu prudent et écrit qu’on a de bonnes statistiques. Je note toutefois que pour 1/5 des cas (5 sur les 25 décrits), les incertitudes de mesure (et/ou théorique) sont telles que le résultat n’est pas donné et que pour 3 cas (WW/ZH, WW/ttH et tautau/WH), l’écart entre la mesure et la théorie semble significatif ou du moins il est supérieur à environ 2 sigma.
Quel commentaire cela peut-il amené? A-t-on vraiment tout compris avec le modèle standard? Peut-on vraiment dire qu’on a découvert le boson de Higgs? Peu-être cela mériterait un complément d’informations pour mieux saisir les différentes propriétés possibles du boson de Higgs tel que le suggère la physicienne interrogée en fin de vidéo…
Très cordialement, merci encore pour ce super travail d’investigation et vulgarisation!
Sur le premier point, il y a bien sûr le fait qu’à l’époque du design du LHC, on ne connaissait pas du tout les masses possibles pour le Higgs, mais aussi que l’énergie de collision influence les taux de production.
Je n’ai pas vraiment trouvé d’équivalent du graphe que je montre qui irait en dessous de 6 TeV, mais on peut imaginer que les taux de collision diminuent (en échelle log) et vu la rareté des événements…
Sur le second point, ça colle en effet surtout bien sur une petite partie des modes, mais ce sont de loin les plus fréquents. Donc pour ceux pour lesquels il y a un écart supérieur à 2 sigma, c’est surtout à mon avis dû au très petit nombre d’événements. A mon avis pas de quoi s’affoler, mais évidemment tout le monde espère qu’une anomalie sera vue 🙂
Super. merci pour cette super vidéo et cette super visite. Cela donne envie de s’y intéresser encore plus 🙂
Fascinant. Merci de nous avoir partagé ces informations. Je suis bouche bée face aux moyens techniques et intellectuels mis en œuvre pour détecter l’invisible.
Si vous avez une petite minute s’il vous plaît, j’aurai deux petites questions.
Quel est le devenir du LHC maintenant que les analyses sont faites et que nous avons semble t il atteint la limite de ses instruments.
Pour finir, je ne saisi pas bien comment a t on pu localiser dans l’espace les « traces » des trajectoires des particules isolées après collision. C’est quand même fichtrement petit. Je n’aurai pas le toupet de vous demander de me l’expliquer mais tout au moins si il existe des articles publics à votre connaissance qui traiteraient du sujet je suis preneur.
Bien à vous.
Quel travail exceptionnel ! Merci à David et à son équipe pour cette présentation du CERN.
Et quel surprise d’apercevoir, lors de la séquence filmée à CMS, les collègues installer nos nouvelles chambres à Muon (basées sur la technologie des GEMs), que j’ai eu la chance et l’honneur de développer pendent les 8 dernières années !
Encore bravo!
Merci beaucoup !