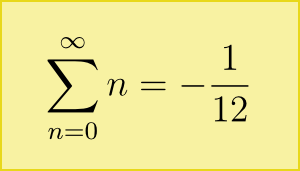 Les mathématiciens sont parfois un peu fêlés. En tout cas ils aiment bien essayer de repousser les limites de notre compréhension, quitte à défier le sens commun. Prenez par exemple la somme suivante : 1+2+3+4+5+6+7… et ainsi de suite. Combien vaut cette somme ?
Les mathématiciens sont parfois un peu fêlés. En tout cas ils aiment bien essayer de repousser les limites de notre compréhension, quitte à défier le sens commun. Prenez par exemple la somme suivante : 1+2+3+4+5+6+7… et ainsi de suite. Combien vaut cette somme ?
Je pense que n’importe quel écolier censé répondrait « l’infini ». Eh bien oui, mais non. Les mathématiciens ont réussi à prouver que cette immense somme vaut en fait … -1/12 ! Nous allons nous aussi le démontrer, et rassurez vous, dans ce billet on ne va utiliser que l’addition !
Edit du 19/01/2014 : après toutes les controverses suscitées par ce billet, j’ai décidé d’en écrire un autre pour justifier pourquoi ce que je raconte ici n’est pas juste un délire de mec qui manipule des objets mathématiques n’importe comment. Vous pouvez commencer par lire ce billet, mais si cela vous indigne et que vous voulez creuser, n’oubliez pas d’aller lire la suite ici : Le scandale des séries divergentes !
Échauffement, niveau 1
A titre d’échauffement, commençons par une somme un peu plus simple :
1 – 1 + 1 – 1 + 1 – 1 + …
Combien vaut cette somme ? Les plus malins remarqueront que la valeur de cette somme oscille entre 0 et 1 au fur et à mesure qu’on lui ajoute des termes. Si on veut vraiment affecter une valeur « moyenne » à cette somme infinie, on peut taper entre les deux et choisir 1/2.
Eh bien on peut en fait rigoureusement démontrer que cette somme vaut bien 1/2. Voici l’idée : appelons A cette somme, on pose donc
A= 1 – 1 + 1 – 1 + 1 – …
On peut ensuite observer que
A = 1 – 1 + 1 – 1 + 1 – … = 1 – (1 – 1 + 1 – 1 + 1 – …)
mais on reconnait que le terme entre parenthèses n’est autre que A lui-même, on a donc l’égalité
A = 1 – A
et vous pouvez facilement résoudre cette équation pour trouver A = 1/2. Facile et amusant, non ? Alors passons au niveau suivant.
Échauffement, niveau 2
Considérons maintenant la somme
B = 1 – 2 + 3 – 4 + 5 – 6 + 7 – …
Il s’agit encore d’une somme oscillante, mais cette fois-ci les oscillations deviennent de plus en plus grosses ! Cette fois-ci on remarque que
B = 1 – (2 – 3 + 4 – 5 + 6 – 7 +…)
et en décomposant en deux morceaux le terme entre parenthèses on a
B = 1 – (1 – 2 + 3 – 4 + 5 – 6 + 7 – …) – (1 – 1 + 1 – 1 + 1 – …)
Or ici on reconnait dans la première parenthèse la somme B dont on est parti, et dans l’autre parenthèse la somme A que l’on a évaluée au paragraphe précédent. On a donc
B = 1 – B – A
Comme on a calculé que A vaut 1/2, on en tire B = 1 – B – 1/2 et donc B = 1/4. Vous voyez qu’avec de simples opérations arithmétiques, on peut attribuer une valeur bien définie à cette somme infinie oscillante !
Passons aux choses sérieuses
Venons-en à notre somme monstrueuse, et appelons la S.
S = 1 +2 + 3 + 4 + 5 + 6 + …
Cette fois ci, la somme n’oscille plus : elle file carrément vers l’infini à grande vitesse ! Et pourtant voici ce que l’on peut faire : prenons la somme S et retirons-lui la somme B
S – B = (1 +2 + 3 + 4 + 5 + 6 + …) – (1 – 2 + 3 – 4 + 5 – 6 + …)
Vous voyez que les termes impairs se compensent et que les termes pairs sont doublés, on a donc
S – B = 2 * (2 + 4 + 6 + 8 + …) = 4 * (1 + 2 + 3 + 4 + …)
et ici à droite on reconnait entre parenthèses notre somme S ! On a donc
S = B + 4S
ou encore S = -B/3. Comme on a vu que B = 1/4, on arrive donc au résultat tant attendu
S = – 1/12. CQFD !
Cela peut vous paraître choquant, vous pouvez chercher la faille, ou vous imaginer que l’on peut démontrer n’importe quoi de ce genre en tripotant des sommes infinies. Eh bien non, si on respecte quelques règles élémentaires, quelle que soit la manière dont on s’y prend, on trouve que si on veut affecter une valeur finie à cette somme monstrueuse, alors -1/12 est l’unique valeur qui colle.
Tout cela a-t-il un sens ?
 Du point de vue strictement mathématique, on peut donner un sens formel bien défini à ces calculs. Il suffit juste de généraliser un peu la notion de somme infinie. Ce qui est plus drôle, c’est que cette somme infinie bizarre joue aussi un rôle important en physique théorique.
Du point de vue strictement mathématique, on peut donner un sens formel bien défini à ces calculs. Il suffit juste de généraliser un peu la notion de somme infinie. Ce qui est plus drôle, c’est que cette somme infinie bizarre joue aussi un rôle important en physique théorique.
Pour ma part, je l’ai croisée pour la première fois lors d’une étude sur l’effet Casimir. Cet effet (qui n’a rien à voir avec l’île aux Enfants) a été prédit par le physicien hollandais Hendrik Casimir, et prévoit que deux plaques parallèles conductrices placées dans le vide vont s’attirer à cause des fluctuations de l’énergie du vide (énergie dont je parlais dans ce billet).
Et pour calculer la force subie par les plaques, on utilise l’égalité 1 + 2 + 3 + 4 + … = -1/12 ! Et ça marche, car cette force a été mesurée expérimentalement !
 Mais il existe une autre branche de la physique où cette égalité joue un rôle essentiel, il s’agit de la fameuse théorie des cordes. Comme vous le savez peut-être, cette théorie affirme nous vivons dans un monde à 26 dimensions (ou 10 ou 11, c’est selon). Les cordistes aiment dire que c’est ce que « prédit » la théorie, mais la réalité est un peu différente : ce nombre de dimensions n’est pas une prédiction de la théorie, mais plutôt un prérequis pour que la théorie ait mathématiquement un sens.
Mais il existe une autre branche de la physique où cette égalité joue un rôle essentiel, il s’agit de la fameuse théorie des cordes. Comme vous le savez peut-être, cette théorie affirme nous vivons dans un monde à 26 dimensions (ou 10 ou 11, c’est selon). Les cordistes aiment dire que c’est ce que « prédit » la théorie, mais la réalité est un peu différente : ce nombre de dimensions n’est pas une prédiction de la théorie, mais plutôt un prérequis pour que la théorie ait mathématiquement un sens.
J’ai déjà eu l’occasion d’évoquer cette histoire (dans ce billet), mais en gros ce qu’il faut savoir, c’est que si vous essayez de construire une théorie des cordes en dimension D=4, ça ne marche pas, car on trouve plein d’infinis partout. On pourrait être tentés d’abandonner l’idée, sauf qu’un jour quelqu’un a remarqué que les infinis disparaissaient si on choisissait D=26. Et c’est comme ça que les théoriciens des cordes, pour sauver leur belle théorie, ont décidé de se placer en dimension D=26 et de continuer l’aventure comme si de rien n’était.
Mais au fait, pourquoi D = 26 est-elle la dimension magique dans laquelle la théorie marche sans que les infinis apparaissent ? Si on fait le détail du calcul, on trouve que le terme infini qui fout le bazar est en fait proportionnel à
\(\left[1 + \frac{D-2}{2}(1+2+3+4+5+6+7+…)\right]\)
or si vous observez cette équation deux minutes, et que vous admettez que 1 + 2 + 3 + 4 + … = -1/12, vous remarquez que tout ce terme devient nul pour D=26, et les infinis disparaissent de la théorie ! Voilà d’où vient le nombre magique, appelé « dimension critique ». (Pour les esprits pointilleux, j’ai raconté ici le calcul tel qu’il se présente pour la théorie dite des « cordes bosoniques », qui est la plus simple. On sait depuis longtemps que cette théorie ne fonctionne pas pour d’autres raisons, et on favorise plutôt les théories « supersymétriques » pour lesquels le nombre magique de dimensions est 10, mais l’idée est la même.)
Pour les plus courageux, je propose deux pistes pour aller plus loin : l’une est mathématique (et parle de la définition formelle de ces sommes infinies pas si infinies), l’autre est physique et parle de l’effet Casimir, et nous donne une vision amusante sur ce que signifie vraiment ce -1/12.
Pour aller plus loin : une justification mathématique
Si vous n’êtes pas convaincus qu’assigner des valeurs finies à ces sommes infinies peut avoir un sens, voici quelques éléments sur le formalisme mathématique sous-jacent.
Si on considère une suite \((a_n)\), on dit généralement que la série \(\sum a_n\) est (simplement) convergente si on peut assigner une limite à la suite des sommes partielles.
\(s_n = \sum_{i=0}^{n} a_i\)
Pour les suites \((a_n)\) pour lesquelles la série est simplement convergente, appelons \(\sum\) l’opérateur qui associe la limite de la suite des sommes partielles. Mais il existe plein de \((a_n)\) pour lesquelles cette condition n’est pas vérifiée, et les 3 exemples de ce billet en font partie.
La question que l’on peut se poser est : existe-t-il une généralisation de l’opérateur \(\sum\) qui soit définie sur un ensemble plus large que les séries simplement convergentes, mais qui bien sûr coïncide avec \(\sum\) sur cet ensemble. Petite contrainte, on ne veut pas de n’importe quel opérateur, on cherche un opérateur linéaire, c’est-à-dire que si on additionne deux suites, les « sommes » s’additionnent (et pareil avec la multiplication par un scalaire). C’est parce qu’on demande ces conditions de linéarité que les manipulations proposées dans ce billet sont correcte, et montrent que si on arrive à trouver un opérateur linéaire qui est définit pour 1 + 2 + 3 + 4 + … alors la valeur que cet opérateur doit affecter cette somme ne peut pas être autre chose que -1/12.
Pour illustrer cette idée d’opérateur qui généralise \(\sum\), une solution possible est d’utiliser la convergence dite « de Cesaro ». Ce dernier a proposé que l’on associe à une suite \((a_n)\) le nombre qui soit la limite de la moyenne de ses sommes partielles. On définit donc l’opérateur
\(C(\{a_n\}) = \lim \frac{s_1 + s_2 + … + s_N}{N}\)
L’opérateur \(C\) généralise \(\sum\) mais coïncide avec lui pour les séries simplement convergentes. La généralisation permet ainsi de calculer 1 – 1 + 1 – 1 + 1 – … C’est ce qui se cachait derrière l’idée de « la somme oscille entre 0 et 1 ».
Autre extension encore plus générale, la convergence d’Abel, où l’on définit l’opérateur A de la manière suivante
\(A(\{a_n\}) = \lim_{x\to1^-} \sum_n a_n x^n\)
Dans le deuxième exemple que j’ai donné, on peut se convaincre que la valeur 1/4 est obtenue comme convergence au sens d’Abel de la série entière de \(\frac{1}{1+x^2}\).
Pour la somme 1+2+3+4+5+…, il faut chercher encore plus général si on veut donner une justification formelle. On peut par exemple utiliser ce qu’on appelle la régularisation par la fonction zeta de Riemann
\(\lim_{s\to 0} \sum a_n n^{-s}\)
Dans le cas de la suite \(a_n=n\), on obtient donc
\(\lim_{s\to 0} \sum n^{1-s} = \lim_{s\to 0} \zeta(s-1)\)
La limite de cette expression correspond alors la fameuse fonction zeta de Riemann, évaluée en -1, et pour laquelle il existe un prolongement analytique qui vaut justement -1/12.
Bon assez de maths, passons à la physique !
Pour aller plus loin : une justification physique
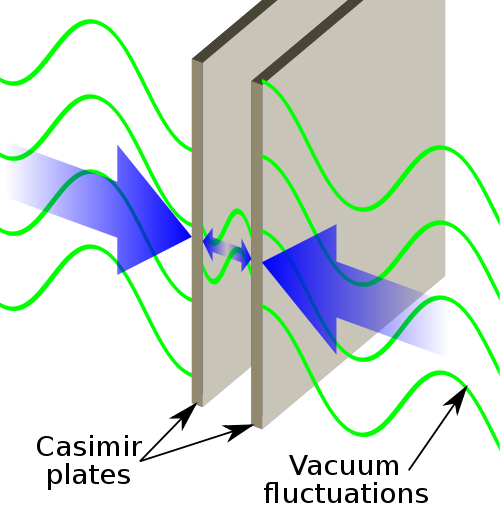 Pour ceux qui ne connaissent pas cette bizarrerie, l’effet Casimir prédit que deux plaques conductrices placées dans le vide à distance L l’une de l’autre s’attirent avec une force qui décroit quand L augmente. Hendrik Casimir a proposé cet effet en le justifiant par les variations de l’énergie de point zéro du vide situé entre les plaques.
Pour ceux qui ne connaissent pas cette bizarrerie, l’effet Casimir prédit que deux plaques conductrices placées dans le vide à distance L l’une de l’autre s’attirent avec une force qui décroit quand L augmente. Hendrik Casimir a proposé cet effet en le justifiant par les variations de l’énergie de point zéro du vide situé entre les plaques.
On sait que les modes de vibrations du champ électromagnétique quantique dans le vide se comportent chacun comme un oscillateur harmonique quantique, et que – contrairement à un oscillateur classique – l’état de plus basse énergie possède une énergie non-nulle. Quand deux plaques sont à distance L l’une de l’autre, à cause des conditions aux limites les modes du champ qui peuvent exister entre elles sont restreints aux longueurs d’ondes qui sont des fractions entières de L. Si on ne considère qu’une dimension d’espace, l’énergie de point zéro du mode \(n\) est égale à
\(E_n = \frac{1}{2} \hbar c \frac{n\pi}{L}\)
Si on somme sur tous les modes, on a donc l’énergie de point zéro totale en fonction de la distance entre les plaques \(L\) qui est égale à
\(E(L) = \frac{1}{2} \hbar c \frac{\pi}{L} \left(\sum_n n\right)\)
Si on ne veut pas trop réfléchir, on peut utiliser la formule magique \(\sum_n n = -1/12\), et sortir
\(E(L) = – \frac{1}{24} \hbar c \frac{\pi}{L}\)
On peut ensuite en tirer la force qui s’exerce sur la plaque en dérivant l’énergie par rapport à L.
\(F(L) = \frac{1}{24} \hbar c \frac{\pi}{L^2}\)
Mais si utiliser l’égalité \(\sum_n n = -1/12\) vous pose problème, on peut chercher une justification plus physique. Quand les plaques sont à distance \(L\) l’énergie qu’on vient de calculer semble infinie. Mais si on éloigne les plaques à grande distance, il y a toujours une énergie volumique associée aux modes du champs électromagnétique. La différence est que dans cette situation les modes ne sont plus quantifiés. Il faut donc essentiellement remplacer \(\sum_n n\) par \(\int x dx\). On obtient là aussi quelque chose d’infini, mais d’un peu plus gros. Maintenant si on prend cette situation comme point de référence et qu’on s’amuse à faire la différence entre les deux situations (plaques à distance L et plaques « très loin ») on trouve
\(\Delta E(L) = \frac{1}{2} \hbar c \frac{\pi}{L} \left(\sum_n n – \int_0^{+\infty} x\ dx\right)\)
On soustrait donc deux infinis…comment faire ?
Il se trouve qu’on est sauvés par une formule mathématique bien pratique, que l’on croise dans les cours d’analyse en licence, et qui s’appelle la formule d’Euler-MacLaurin. Cette formule permet d’estimer la différence entre une somme discrète sur une fonction et l’intégrale correspondante. Elle dit notamment que pour une fonction \(f\)
\(\sum_n f(n) – \int_0^{+\infty} f(x) dx = \frac{1}{2} f(0) – \frac{1}{12} f'(0) + …\)
où je vous épargne les termes liés aux dérivées d’ordre supérieur. Ce qu’il y a d’amusant, c’est que si on applique (illégalement) cette formule pour la fonction f(x)=x, on trouve
\(\left(\sum_n n – \int x\ dx\right) = – 1/12 \)
Et on retombe bien sur l’énergie de Casimir.
Personnellement je trouve que ce calcul nous éclaire sur l’origine profonde de -1/12. En fait la somme 1 + 2 + 3 + 4 + … est bien infinie, mais -1/12 est ce qui la sépare de \(\int x dx\) qui est aussi infini, est que l’on peut voir comme une base que l’on soustrait. Dans le cas de Casimir, il s’agit bien d’ailleurs du niveau énergétique « de base », quand les plaques sont très éloignées.
Autre manière de le dire, on trouve que 1 + 2 + 3 + 4 + … est infini, mais égal à -1/12, modulo \(\int x dx\).
Vous avez tenu jusque là, je vous félicite ! Promis un jour je ferai un billet compréhensible sur l’effet Casimir !



415 Comments
J’émets une réserve quant à vos calculs qui au demeurant sont justes. Je pense que les valeurs de S comme de B prises séparément restent incalculables car infinies ; et que cette égalité S = – 1/12 n’est pas le résultat de la valeur de S, mais plutôt le résultat du rapport de grandeur existant entre S et B.
En analysant cette suite numérique (1+2+3+4+5+6+7+…) deux choses sautent aux yeux. La première est le résultat qui est nécessairement positif ; et la seconde est l’infini qui par définition signifie : « Qu’on ne peut évaluer, qui est incalculable. »
Or cette égalité S = – 1/12 aboutit au résultat suivant : – 0.083 qui plus est un résultat négatif.
Bien à vous…
je suis d’accord.
PS: Tout ce que je dis doit être considéré comme faux
Bonjour,
j’ai également une réserve liée aux infinis. Lorsqu’on compte avec les nombres ordinaux, l’addition n’est plus commutative : w + 1 n’est pas 1 + w. Or quand on prend les termes des sommes deux à deux on commute à chaque fois.
Je suis plus du camp de ceux qui pensent que ce genre de calculs exploite les limites des définitions des opérations et des nombres.
Sauf qu’il y a bien l’expérience de Casimir. C’est effarant. L’univers entier nous nargue au niveau métaphysique.
Pareil. Le fait d’ajouter des chiffres à une liste change la définition de la liste, fusse-t-elle infinie. Quant à la l’utilisabilité des résultats de ce genre, ce ne sera pas la première fois qu’un résultat faux abouti à une solution valide.
fût-elle…
Si S= 1+2+3….=-1/12
Donc soit S’= 1+2+3+4+5 par example
Donc S’= 15 bien sûr
Alors S = S’+ N
Les termes de S sont €IN
Donc S€ IN et S’€ IN
DONC N= S-S’= -1/12 -15= -127/12 ce qui est absurde car on negligeant les 5 premiers termes la Somme he doit etre changee car l’infinie est ouvet et on ajoute un terme on plus et on gagne de nouveau plus de 15 c.a.d N =-1/12
Pour moi, ton N est correct et vaut bien -1/12-15=-181/12 (et non 127/12 mais qu’importe)
Par exemple, la somme des 1/k^n vaut pi^2 / 6. Alors si tu commences la somme à 2, tu obtiens bien pi^2 / 6 – 1.
Je vois pas pourquoi en rajoutant ou en enlevant un terme à une somme infinie ça ne changerait pas la somme.
Bonjour,
Je suis d’accord avec Kristen sur le non respect des règles sur l’infini.
Je pense que dès le départ il y a un non dit concernant l’infini, et celui-ci permet de modifier une série à son gré sans respect de cet infini. A = 1 – 1 + 1 – 1 + 1 – … = 1 – (1 – 1 + 1 – 1 + 1 – …) n’est pas pour moi un égalité.
Exemple : A = 1 – 1 + 1 – 1 + 1 – … = – 1 + 1 – 1 + 1 – 1 + 1… = – 1 + (1 – 1 + 1 – 1…) = – 1 + A -> A = – 1 + A -> 0 = – 1
CQFD
Je pense que c’est prendre le lecteur pour un abruti quand on utilise le calcul de limites à l’infini sur une suite et une série pour justifier
1+2+3+4+….= -1/12 avec https://s0.wp.com/latex.php?latex=C%28%5C%7Ba_n%5C%7D%29+%3D+%5Clim+%5Cfrac%7Bs_1+%2B+s_2+%2B+…+%2B+s_N%7D%7BN%7D&bg=ffffff&fg=444444&s=0
en effet 1+2+3+4+….+n= n(n+1)/2 mais j’ai pas le droit de faire un calcul de limite lorsque n tend vers l’infini?! car cela démontre la série tend vers l’infini quand n tend vers l’infini! et pas -1/12!! Ceci dit, la démonstration physique me plait et justifie le -1/12 effet Casimir Mais c’est une conjecture pas une démonstration mathématique. Connaissez vous d’autres expériences physiques indépendantes de l’effet Casimir qui apportent des conjectures validant cette expression? Une hirondelle ne fait pas le printemps mais restons l’esprit ouvert mais attention danger!!
En fait la série [(-1)^n] est divergente puisque son terme général ne tend pas vers 0. C’est là toute l’ambiguïté de cette démonstration qui devrait commencer par « si cette somme existe » alors elle vaut 1/2 du fait de la démonstration qui tient la route… Mais cette somme existe-t-elle ? Non évidement au sens de la somme d’une série convergente, mais, et c’est là que la démonstration devient intéressante, existe-t-il une mathématique dans laquelle cette somme existe ?
En s’ouvrant à l’idée de l’existence d’une telle mathématique, on s’ouvre peut-être un nouveau champ d’expérimentations…
C’est ce que cherche à mettre en évidence David !
A = 1 – 1 + 1 – … est différent de -1 + 1 – 1 +…, non ?
D’ailleurs, cette dernière est -A.
-A = -(1 – 1 + 1 – …) = -1 + 1 – 1 + …
Ton CQFD ne fonctionne pas.
Bonjour,
il suffit de dire que l’en semble N des entiers naturels dans lequel se trouvent tous les chiffres de cette somme est un ensemble fermé et donc que le résultat y figure également. Faire des sommes avec des infinis (7…) ne correspond à rien mathématiquement et la démonstration est donc fausse.
Pourquoi dites-vous « (illégalement) » ?
Pourquoi serait-ce illégal d’appliquer Euler-McLaurin à f(x) = x ?
Oh ben moi je suis physicien, donc ça fait longtemps que je ne vérifie plus les conditions d’application des théorèmes, mais quand on démontre cette formule, il doit quand même y avoir quelques clauses restrictives du genre « f est intégrable » et la série doit être absolument convergente. Donc l’utiliser comme ça à la hussarde doit être illégal 🙂
D’après Wikipédia, la seule condition est que la fonction soit dérivable une infinité de fois (ce qui est vérifié ici). Pour l’intégrabilité et la convergence, je dirais que c’est pas nécéssaire, vu qu’on cherche pas à ce que les 2 termes convergent, mais à faire un développement asymptotique de la somme en fonction de l’intégrale. Je pense que le mot (illégalement) vient du fait qu’il l’utilise à l’ordre 1 😀
Mais je me pose une question :
A = 1 – 1 + 1 – 1 + 1 – … = 1 – (1 – 1 + 1 – 1 + 1 – …)
A serait pas égal à 1-(1+1-1+1-1…) se qui ferait A = 1+A ?
« A = 1 – 1 + 1 – 1 + 1 – … = 1 – (1 – 1 + 1 – 1 + 1 – …)
A serait pas égal à 1-(1+1-1+1-1…) se qui ferait A = 1+A ? »
Bah non, ça fait A = A = 1 – (A) soit A = 1 – A
très d’accord!!!
Bizarre, quand j’étais petit on me disait qu’une somme arithmétique de 1 à n était n.(n+1)/2. De fait, si je fais tendre n vers l’infini, la somme tend vers… l’infini (aucun problème de limite).
De plus, et d’accord avec Kristen, une somme de termes positifs doit être positive.
merci pour votre blog
J’allais émettre les mêmes réserves qu’Olivier et Kristen. Je pense que le problème est dans le vocabulaire utilisé. La somme n’est pas « égale », je peux éventuellement accepter le fait qu’on attribue une valeur à cette somme mais ce n’est certainement pas une égalité au sens usuel du terme. La somme S est une somme infinie comme l’a rappelé Olivier.
J’avais déjà vu passer ce truc et il me met un peu mal à l’aise (par contre cet article est très bien détaillé et agréable à lire, merci!)… Mais pas tant pour les remarques précédentes. A ce titre, quelques réponses :
@Kristen : l’infini veut pas dire « qu’on ne peut évaluer, qui est incalculable », on considère même qu’une suite qui converge vers l’infini a une limite, elle est juste « infinie », c’est à dire pour faire simple, plus grande que tous les nombres. Quant à faire des calculs avec l’infini, on peut tout à fait en faire, il faut juste faire attention, cf un de mes articles sur le sujet : http://nicotupe.fr/Blog/2012/02/podcastscience-74-linfini-quand-il-ny-en-a-plus-il-y-a-cantor/
@Sham & @Olivier : c’est un des trucs qui me gène sur cet exemple, il génère à mon avis plus de confusions qu’il apprend de choses… On a le droit de dire « égal » mais on change la définition du terme égal. Et plus gênant à mon sens, on change la limite de suites dont on connait très bien la convergence (on remplace l’infini par -1/12, ce qui a en plus le mauvais goût d’être négatif…). Pour les sommes qui ne convergent pas (comme la somme des 1 et des -1) trouver une manière de leur donner une valeur n’est à la limite pas choquant, il rajoute de la connaissance là où on n’en avait pas mais pour les suites convergentes c’est plus gênant.
D’autant que l’explication consistant à dire :
A = 1 – A alors A = 1/2
est une formule raccourcie pour dire :
Si la somme A à une limite et si cette limite est finie, alors si A = 1 – A, on a A = 1/2
Donc, et comme c’est très bien dit, avec cette démonstration on montre seulement que la seule limite finie acceptable de cette somme est 1/2 mais absolument pas que cette somme a une limite et encore moins que cette limite est finie. Donc cette démonstration n’élimine pas du tout le cas A = infini!
La bonne explication est alors donnée ensuite, dans la partie « Pour aller plus loin : une justification mathématique ».
quand il y en a plus il y a Cantor me plait bien comme titre 😉
je trouve tout de même que l’article n’est pas assez clair ou prête facilement à confusion. la section pour aller plus loin est effectivement très intéressante, il aurait juste fallu prendre un peu plus de précautions dans la partie grand public (à mon goût).
Je suis complètement d’accord avec toi 🙂
heum, il me semble que ne serait-ce que dans l’exemple A, il y a l’erreur classique de penser que A = 1-A… Ne serait-ce pas plutôt A = 1-1 + A ?
Ce qui serais bien plus correct…
Le problème en revient à la notation non mathématique d’une telle somme.
Elle devrait être décrite (si non avec les symboles approprié) telle quelle : Soit A une somme infinie de 1 et de -1 de telle sorte qu’à chaque -1 on ajoute 1, et à chaque 1 ou lui soustrait 1. Ce qui temps bien entre 1 et 0.
Cette « suite » est utilisée dans le paradoxe de la lampe de thomson à propos ses supertasks, il me semble… (elle inclue donc une notion de temporalité)
Bonjour,
il existe un théorème mathématique qui démontre que la somme d’une série convergente mais pas absolument convergente peut être rendue égale à n’importe quelle valeur réelle par changement de l’ordre de sommation. Donc en ce sens, non seulement la série « 1+2+3+… » ne converge pas, mais la série « 1-2+3-… » n’a pas vraiment de somme.
C’est un point de vue totalement opposé, plus radical d’une certaine manière que le point de vue des commentaires précédents.
Ce qui me paraît intéressant, dans le sens exposé dans l’article de David, c’est la définition de la somme retenue. Le choix d’une série de fonctions dont la limite « terme à terme » est la série à calculer est arbitraire, mais on ne change absolument pas l’ordre de sommation.
Est-ce que cela suffit à rendre la somme indépendante du choix de la série de fonctions ? C’est ce que prétend David, si je comprends bien. J’ignore si c’est vrai (après tout, les choix présentés sont peu nombreux), mais de deux choses l’une :
* soit c’est effectivement le cas, auquel cas on peut faire des calculs que l’on s’interdit généralement de faire, et cela est rassurant pour la pertinence des résultats de théorie quantique des champs (QFT) ;
* soit ce n’est pas le cas, et dans ce cas le fait que les prévisions de la QFT soient souvent conformes aux expériences suggère que le choix des séries de fonctions a un sens profond, qui peut guider vers une théorie mathématiquement mieux fondée que la QFT.
SG
Bonjour.
Les mathématiques (et les mathématiciens) me fascinent mais je ne les connais ni ne les pratique suffisamment pour pouvoir faire le moindre commentaire sur ce billet. Je veux dire de commentaire sur la partie mathématiques. Le raisonnement que vous faites me semble juste, mais en lisant les réponses de Kristen et Olivier je trouve qu’eux aussi ont raison. Alors je ne sais plus qu’en penser. Par contre, je voudrais faire un commentaire sur la physique et les physiciens qui utilisent ce type de résultats, ou de raisonnements, mathématiques pour concocter des théories. Je ne suis pas beaucoup plus calé en physique qu’en mathématiques et ma connaissance de la théorie des cordes n’a jamais dépassé ce que j’ai pu en lire dans la revue Science & Vie. Or, c’est la première fois que je lis – ici dans ce billet – que le nombre de dimensions dont il est question dans cette théorie n’est pas une prédiction de celle-ci mais un prérequis mathématique pour qu’elle fonctionne. Cela me renforce dans l’idée que j’ai depuis longtemps que les physiciens se fourvoient peut-être en pensant que les mathématiques doivent forcément représenter des choses qui existent dans le réel. C’est un vieux débat : est-ce que les mathématiques préexistent à l’homme, qui ne fait alors que les découvrir, ou bien est-ce lui qui les invente, et ce n’est alors qu’un hasard si certaines propriétés mathématiques se retrouvent (ou semblent se retrouver) dans la nature. Je penche pour la deuxième hypothèse : aucune forme de mathématique n’existe dans la nature, c’est l’homme qui les invente, et il trouve parfois utile de les appliquer à l’explication de la nature. Mais est-ce que toutes les mathématiques trouvent leur application dans l’explication de la nature ? Je ne le crois pas. Par exemple, en restant à un niveau élémentaire des maths, les quatre opérations arithmétiques. De l’addition, de la soustraction, de la multiplication et de la division, seules les deux premières correspondent à quelque chose qui existe dans la nature. Je peux trouver des additions dans la nature. Par exemple, la reproduction des êtres vivants est une addition. Même ce qu’on appelle la « division » des cellules n’est en réalité qu’une addition : au départ il y a une cellule, puis il y en a deux, puis les deux, en se scindant, en donnent quatre, etc. Il s’agit bien d’une suite d’additions : 1 + 1 = 2, 2 + 2 = 4, 4 + 4 = 8, etc. Ensuite, l’homme invente les maths et il dit : « les cellules se sont multipliées ». Sauf que la nature ne sait pas faire de multiplication. Elle ne sait qu’ajouter ou soustraire (dans le règne du vivant, par exemple, la soustraction c’est la mort). Je pense qu’il en est probablement de même pour ce qui concerne les dimensions. Je ne veux pas nier a priori que notre univers possède plus de quatre dimensions (en comptant le temps comme une dimension), mais je veux tout de même garder en tête l’hypothèse que des théories qui demandent 10, 12 ou 24 dimensions pour pouvoir fonctionner ne sont rien de plus que des jeux spéculatifs n’ayant que peu de rapport avec la réalité de la nature. D’ailleurs, il semble que les résultats rapportés par le satellite Planck sur le « fond diffus cosmologique » remettent fortement en cause la fameuse (fumeuse) théorie des cordes.
c’est effectivement l’homme qui invente les mathématiques, mais en se basant sur des choses visibles dans la nature. En fait, les mathématiques telles qu’on les connait se basent sur 5 ou 6 axiomes, qui sont des choses admises directement par observation dans la nature. Tout le reste découle de là. Seulement, si on considère que l’un de ces axiomes, une seule de ces observations naturelles, n’est pas exacte, on peut recréer un tout nouveau système mathématique, qui pourrait fonctionner tout aussi bien et s’appliquer tout aussi bien à la nature par la suite.
Par exemple, dans la démonstration de cette étrange égalité, on considère qu’une suite non convergente peut avoir une limite finie, ce qui est totalement inexact dans les mathématiques actuelles, puisque les mathématiques telles qu’on les apprends à l’école cherchent à se rapprocher d’une certaine logique. En fait, on pourrait même démontrer que l’assertion « une suite non convergente peu admettre une limite finie » est fausse justement grâce à cet exemple, avec un raisonnement par l’absurde: on obtient qu’une somme de termes positifs est égale à une nombre négatif, c’est absurde, donc c’est faux.
C’est donc une autre forme de mathématiques qui est utilisée ici, avec des axiomes de départ un tantinnet différent, qui peut cependant fonctionner et se retrouver ailleurs (en physique ou dans la nature) bien qu’elle nous paraisse parfois absurde.
Le monde n’est pas régit par une seule loi.
Attention, une suite non convergente (qui alterne de signe comme dans cet exemple) peut avoir une limite finie … (série de Taylor)
Bonjour. Je lis: « aucune forme de mathématique n’existe dans la nature, c’est l’homme qui les invente, »…. Je serai beaucoup plus nuancé. La nature invente énormément de mathématiques. Mais on n’en voit que le résultat des formules cachées. Un jour, on m’a dit: « ce chien est stupide ». Alors j’ai lancé une balle à 20 mètres et ce chien l’a rattrapée au vol. Ce chien venait de résoudre en 2 secondes une équation du second degré à deux inconnues. Idem pour un joueur de tennis ou de foot. L’écriture mathématique n’est qu’une formalisation de ce que la nature a créé. Apparemment, l’homme serait sur Terre la seule créature dotée d’une capacité d’abstraction aussi poussée. Il existe des maths n’ayant aucune application physique ou concrète. Mais la nature, elle, obéit à des règles toujours mathématiques (statistique, géométrie, etc…).
Jure la vie de ta mere
« De l’addition, de la soustraction, de la multiplication et de la division, seules les deux premières correspondent à quelque chose qui existe dans la nature. Je peux trouver des additions dans la nature »
Sachant que la multiplication est sur sorte de « super-addition » (1+1 = 1*2, 2+2 = 2*2 etc), je suis sûre qu’on peut trouver des exemples de multiplications dans la nature.
« mais je veux tout de même garder en tête l’hypothèse que des théories qui demandent 10, 12 ou 24 dimensions pour pouvoir fonctionner ne sont rien de plus que des jeux spéculatifs n’ayant que peu de rapport avec la réalité de la nature »
Je trouve ça très honnête de dire « je veux garder en tête que ».
Je ne pense pas du tout que des théories travaillant sur des dimensions > 4 soient fantaisistes, ou des « jeux spéculatifs », n’ayant que peu de rapport avec la réalité de la nature.
L’être humain perçoit le monde à travers ses sens. Or, ces sens sont purement subjectifs, puisque déjà, biologiquement, il y a des différences entre êtres humains. Bien sûr, on arrive à affirmer des certitudes parce qu’au final, il y a quand même pas tant que ça de différence de perception d’un individu à un autre. Donc en rassemblant la perception de plusieurs dizaines de personnes, il y a de fortes chances pour que ce qui est perçu de la même par tout le monde soit une vérité « absolu ». Entre guillemets, parce qu’il suffit qu’une personne n’aie pas cette perception pour que cette vérité ne soit plus absolue (or, on est 7 milliards sur Terre, et je ne parle que des êtres humains – imaginez si on commence à parler de toutes les espèces vivantes que l’on connaît).
Bref. Pour les êtres humains (et probablement pour quasiment tous les animaux), percevoir le monde en 3 dimensions est possible et naturel. Parenthèse : quand j’y réfléchis bien, un monde en 2 dimensions ne me paraît pas plus naturel qu’un monde en 4 dimensions, bien qu’un monde en 2 dimensions me paraît beaucoup facile à appréhender (forcément, ça simplifie toutes les équations).
De mon point de vue, il n’y a pas de raisons pour qu’il existe une 4e, une 5e, une 6e ou encore d’autres dimensions. On ne les perçoit pas, tout simplement. Enfin… la 4e, pour la dimension du temps, un peu quand même, mais ça commence à devenir contre-intuitif quand on comprend qu’on ne voit que le passé, jamais le présent. Regarder les étoiles l’illustre bien et rien que regarder le Soleil est significatif (ses rayons mettent 8mn à arriver sur Terre, si je dis pas de bêtises).
Corrections :
« Il y a de fortes chances pour que ce qui est perçu de la même *manière* par tout le monde […] »
« De mon point de vue, il n’y a pas de raisons pour qu’il *n’existe pas* de 4e, […] ».
Je me permet de donner mon avis aussi. L’erreur du résonnement apparaît dès le début. le calcul A=1-A est juste mais ne peut être simplifié que si les terme A sont des éléments réels (ce n’est pas le cas) ou des séries convergentes (et … ce n’est pas la cas non plus). Donc la simplification ne tient pas. Ceci fait penser à 2*0=1*0 donc 2=1. La première égalité est juste mais ne peux pas être simplifiée pour donner la deuxième.
Pour ce qui est des interprétation physique, je ne m’y connais pas assez pour ça
euuuh, 2*0=1*0 est équivalent à 2=1? mais depuis quand on peut diviser par 0? ;P
sinon, je suis d’accord avec toi =)
C’est justement ça le défaut signalé (sous forme de comparaison)
Je suis surpris que personne ne mette en doute l’existence (pas les propriétés) du nombre A dès le premier paragraphe.
Tout le raisonnement (c’est sympa de l’appeler raisonnement) ne parle de rien.
Retenons que les élément de l’ensemble vide ont toutes les propriétés agréables qu’on veut leur prêter. Sauf une : l’existence.
Pour les non matheux qui se sont exprimés ici : le rôle des maths est de clarifier les notions avec exactitude.
Prétendre que A= Infini et S=-1/12 ne sont pas des égalités de même nature prouve simplement que l’usage du signe = n’était pas approprié dans l’une au moins de ces deux écritures. Et les vrais spécialistes d’une disciplines sont conscients de leurs abus d’écriture …
@Gardox :
Avant d’être réfractaire à une idée qui paraît complètement folle et de vouloir chercher la petite bête, je t’invite fortement dans ce cas à lire le reste de l’article. Même si j’ai pas tout compris sur la partie « bonus », la phrase de fin est vraiment importante :
Autre manière de le dire, on trouve que 1 + 2 + 3 + 4 + … est infini, mais égal à -1/12, modulo \int x dx.
@Gardox :
Il y a même une suite à cet article : https://sciencetonnante.wordpress.com/2014/01/20/le-scandale-des-series-divergentes.
Mais ici, on ne prend pas la sommation classique. Ici on prend une sommation arbitraire que l’on suppose régulière, linéaire et stable, puis on démontre que si cette série converge vers un réel alors ce réel ne peut être autre que -1/2. C’est tout.
oui et également A=1-A
donc 1=0
Si je vous donne une bille et que je vous la reprends, et ce à l’infini, combien en avez vous?
oups dsl…2A=1
Enfin bon j’ai du mal quand même à me dire qu’il y a un résultat et je me dis intuitivement qu’il doit manquer un élément
Le coup de la somme =-1/12 est très bien expliqué dans le billet. Pour résumer :
– il existe sur l’ensemble des suites dont la série converge un opérateur S (= « somme de la série ») avec tout plein de bonnes propriétés (positivité, permutation avec des limites, etc).
– peut-on prolonger S en opérateur linéaire sur un espace strictement plus grand que celui des séries convergentes ? Oui, on le peut, la théorie des espaces vectoriels nous l’assure. Ce qui est montré ici, est que si on demande en plus que le prolongement (appelons-le T) prenne les mêmes valeurs sur les suites qui ne diffèrent que de quelques « 0 » mis au début (T(1,2,3,4,…) = T(0,1,2,3,4,…)) alors la valeur de T sur la suite (1,2,3,4,…) est forcément celle décrite dans l’article.
Par contre, danger : T n’est plus vraiment une « somme », perd ses propriétés de positivité et de « permutation avec les limites », n’est pas compatible avec les permutations des termes de la suite, etc. Conserver le symbole de sommation pour désigner ce prolongement est donc certes bien pratique, mais un peu gonflé à la fois.
– Et j’insiste pour finir que la propriété
« si on veut affecter une valeur finie à cette somme monstrueuse, alors -1/12 est l’unique valeur qui colle »
ne marche que si on impose le fait que le prolongement prenne les mêmes valeurs sur les suites qui ne diffèrent que de quelques « 0 » mis au début, sinon ça va pas. Vous me direz, « oui mais c’est quand même bien naturel comme condition ». Et là je répond que la propriété de positivité aussi est bien naturelle, ça n’a pas empêché de la perdre quand on a prolongé.
« Conserver le symbole de sommation pour désigner ce prolongement est donc certes bien pratique, mais un peu gonflé à la fois. »
Voila fort bien résumée ce qui me gêne!
Salut stp peut tu m’explique la valeur 1/4 par ruimann?
Mercie pour ce jolie billet qui a comblé le vide qu avait laisser une comferance sur la fonction Zeta oú l on a ait donner ce resultat et depuis ous etes le seul a avoir traiter de ceçi sur le web
Vous êtes en exclusivité sur le sujet
Une chose me choque dès l’échauffement niveau 1…
Prenons un autre exemple :
Une somme très simple : 1 + 1 + 1 + 1 + 1 + 1 +…..
Combien vaut cette somme ? Il apparaît clairement que cette somme tend vers l’infini…
Eh bien on peut en fait rigoureusement démontrer que cette somme vaut 0. Voici l’idée : appelons A cette somme, on pose donc
A= 1 + 1 + 1 + 1 + 1 + …
On peut ensuite observer que
A = 1 + 1 + 1 + 1 + 1 + … = 1 + (1 + 1 + 1 + 1 + 1 + …)
mais on reconnait que le terme entre parenthèses n’est autre que A lui-même, on a donc l’égalité
A = 1 + A
donc A – A = 1 + A – A
d’où 0 = 1
Nous avons donc A = 0 + 0 + 0 + 0 + 0 +….
Trivialement, nous trouvons A = 0.
Facile et amusant, non ?
Amusant mais faux 🙂
En fait ta démonstration ne prouve pas que A=0 mais plutot que si on a le droit de soustraire A de chaque coté de l’égalité, alors 0=1. Or comme 0 n’est justement pas égal à 1, ca prouve qu’une de tes hypothèses est fausse, en l’occurrence, on a pas le droit de soustraire des deux coté cette somme infinie. C’est parfois possible mais pas dans ce cas.
Par contre tu peux t’en servir pour montrer que A n’a pas une limite finie. Si A a une limite finie, A est donc égale à un entier, ce qui fait que tu as le droit de faire les opérations classiques, parmi lesquelles soustraire des deux cotés d’une égalité.
Du coup, ta démonstration peut se réécrire :
Si A a une limite finie, alors 0=1.
Or, encore une fois, comme 0 n’est pas égal à 1 alors, A n’a pas une limite finie, ce qui veut dire que :
– Soit A n’a pas de limite (pas du tout, comme 1-1+1… au sens usuel)
– Soit A a une limite infinie (on est dans ce cas!).
Et remarquons qu’avec une limite infinie, on a bien
infini = infini + 1
Mais on ne peut pas pour autant dire que
infini – infini = 0
En suivant ton raisonnement :
Soit A = 1 + 1 + 1 + 1 + 1 + 1 + …. (cette somme a donc une limite infinie)
Soit S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +….
S = 1 + 1 + 1 + 1 + 1 + 1 + ….. + (0 + 1 + 2 + 3 + 4 + 5 + 6 + ….)
S = A + S
Or S = -1/12 (démontré plus haut…)
Donc -1/12 = A – 1/12
D’où A = 0.
D’où, la somme 1 + 1 + 1 + 1 + 1 + 1 + 1 + …. = 0
Encore plus facile et plus amusant 😀
je répond ici mais répond bien à ta réponse Anne Honyme :
Bah facile et amusant mais on atteint les limites des abus d’écriture qu’on se permet en diffusion des sciences!
Dans A = infini
et dans S = -1/12
le signe « = » ne signifie pas la même chose donc tu peux pas remplacer les deux sommes pareil dans les deux équations et encore moins les additionner (on ne peut toujours pas additionner des pommes et des poires… a part en raisonnant en fruits bien sur!)
Ah ah ! Je ne pensais pas que ce billet provoquerait une telle levée de boucliers ! Alors pour essayer de répondre aux différents points :
Oui, cette somme est bien infinie dans le sens classique du terme. Mais comme je le disais dans la partie « pour aller plus loin », et comme le rappelaient nicotupe et Robyn Slinger, ce qu’on change ici n’est pas la définition du signe égal mais la définition du signe somme.
Mais attention, on ne la change pas n’importe comment !
– D’une part on la *prolonge*, c’est-à-dire qu’appliquée aux suites habituelles, elle donne le même résultat (la somme au sens de la convergence simple).
– D’autre part on demande à ce prolongement de respecter certains critères, essentiellement la linéarité.
Attention en faisant ce prolongement, il y a des propriétés qu’on perd !! Comme le rappelait Stéphane, déjà avec la convergence simple on perd le droit de permuter des termes. Ici on perd la positivité, ce qui je vous l’accorde est un peu perturbant (mais pour moi pas forcément beaucoup plus que la permutation des termes.)
Il existe plusieurs manières plus ou moins puissantes de prolonger (Cesaro, Abel, zeta, peut-être d’autres). Mais si on arrive à faire ce prolongement, on trouve que les valeurs attribuées aux sommes « infinies au sens classique » ne peuvent pas être n’importe quoi, à cause des conditions sus-mentionnées. Tous les prolongements qui marchent en un point donné doivent donner le même résultat.
En l’occurrence, pour 1+2+3+4+5+… (ou plutôt comme on devrait l’écrire S({1,2,3,4,5,6,…}), la valeur ne peut être que -1/12, quelle que soit la technique de prolongement qu’on utilise.
Euler s’était déjà rendu compte il y a 200 ans de ce fait. Il faisait ces manipulations, il savait que c’était illicite, et pourtant il voyait bien que différentes manières de faire le calcul donnaient quand même le même résultat. Donc il se doutait qu’il y avait un truc profond derrière ça.
Il y a deux choses remarquables :
– même si on a pas trouvé la technique de prolongement dont on peut démontrer qu’elle marche, on peut quand même trouver la valeur -1/12 par les manipulations habituelles que j’ai faites dans le billet. Bien sûr elles sont stricto-sensu illicites, mais si on respecte quelques conditions, ces manipulations vont nous donner le résultat du prolongement.
– comme le disait Stéphane, l’unicité de cette manière de prolonger fait que l’on peut tenter d’utiliser ce résultat « en pratique », comme dans certaines théories physiques. C’est ce qu’on fait dans l’effet Casimir, et ça marche ! Ca montre donc qu’une telle « régularisation » des sommes infinies, bien que choquante pour le sens commun, peut avoir sa pertinence pratique.
Désolé d’avoir semé la panique, comme le remarquaient nico et sham, j’aurai peut être dû mettre plus de gardes-fous dans la partie principale 😉
Observons que S=1+2+3+….
=1+(2+3+4+….)
= 1+(1+1+1+….)+(1+2+3+…)
=1+U+S où U=1+1+1 …. Donc 0=1+U donc U=-1.
Mais S=(1+1+1+…..)+(0+1+2+3+…)=U+S
=-1-1/12=-13/12
=-1-13/12=-25/12
= ….
= -(12n+1)/12 pour tout entier naturel n.
Observons que U=1+1+1…..=(1+1)+(1+1)+….=2+2+2 +…. =2U=-2
Or U =(1+1+1)+(1+1+1.+……) =3+U =3+(-2)=1
=4
=7 enfin on dit n’importe quoi
D’ailleurs S = (1+3+5+….)+(2+4+6+….)=(1+1+1….)+(2+4+6+….)+(2+4+6+….)
Donc S=U +4S,=-1-4/12=-4/3
Mais S=
Salut stp peut tu m’explique la valeur 1/4 par ruimann?
@Anne Honyme : dans ton deuxième exemple, c’est la « mise bout à bout » des deux sommes qui est interdite, ça n’est pas une opération linéaire 🙂
Mais je n’exclus pas qu’on trouve une faille dans les raisonnements heuristiques !
et d’ailleurs je ne sais pas s’il existe un prolongement pour 1+1+1+1+1+
La valeur de zeta en zero ? (-1/2) peut être ?
A+B = B+A, n(A+B) = nA+nB etc… Alors pourquoi cette opération n’est-elle pas linéaire?
Bonne remarque. J’aurai du préciser ce qu’on entend par linéaire. Il faut voir l’opérateur « sigma » comme agissant sur l’espace vectoriel des suites réelles. C’est dans ce sens qu’on veut la linéarité c’est a dire que si a=(a0,a1,a2,…) et b=(b0,b1,b2,…) sont deux suites, alors on veut que
S(a+b) = S(a) + S(b)
Dans cette definition, la suite a+b est la suite (a0+b0,a1+b1,a2+b2,…) ce qui n’est pas la meme chose que de « mettre bout a bout » les deux suites (ce qui n’a pas tellement de sens).
Donc si on « additionne » deux sommes infinies, on n’a le droit que de faire des sommes terme a terme, ce qui notamment interdit la reorganisation des termes de la serie (chose qui est deja interdite avec les series convergentes mais non-absolument convergentes)
Ah bien bien ! J’ai lu ça à la mauvaise échelle. Merci !
Merci pour les explications et les commentaires critiques. Le point important selon moi « c’est ce qu’on fait dans l’effet Casimir, et ça marche ! » .
Voilà.
http://passionegypte.wordpress.com/2013/05/24/citation-de-ani/
Pingback: 1+2+3+4+5+6+7+… = -1/12 ! | C@fé ...
Pingback: 1+2+3+4+5+6+7+… = -1/12 ! | Séren...
@David: bravo pour ce chouette billet, je ne connaissais pas ces bizarreries mathématiques et j’ai enfin compris (enfin… un bien grand mot) d’où sort la dimension 26! Et la différence entre somme discrète et intégrale (dans l’annexe 2) éclaire au passage « l’obligation » de quantifier l’énergie pour résoudre le paradoxe du rayonnement du corps noir. Je n’étais pas allé aussi loin dans mon explication, donc merci pour ce complément!
A propos de l’échauffement N°1, on peut également démontrer que le résultat n’est pas 1/2 mais bien 0.
En effet il suffit d’écrire :
1-1+1-1+1-1+………=1+1+1+1+………-1-1-1-1-………=(1+1+1+1+………)-(1+1+1+1+……..) =0
Cela démontre l’incohérence de ce type de raisonnement lorsque l’on touche à l’infini.
La vrai réponse sur cette série oscillante est bien l’indéterminisme 1 ou -1 pour la somme, ce qui peut ouvrir des portes sur l’aspect quantique: un objet quantique dans deux états simultanés.
A méditer !!!!
Rectification : « La vraie réponse sur cette série oscillante est bien l’indéterminisme 1 et 0 ………. »
Manipulation interdite ! Encore une fois ça a l’air totalement anodin, mais on n’a pas le droit de réorganiser les termes de la séries. Même avec des séries simplement convergentes c’est interdit, par exemple
1-1/2+1/3-1/4+…
Si on change l’ordre des termes, on change le résultat !
Ici c’est encore pire, même le parenthesage
(1-1)+(1-1)+…
est une manipulation non linéaire !
Mea Culpa, effectivement l’addition est une opération commutative MAIS pas la soustraction,
Je suis fan de votre blog, merci pour tout.
Ouaf! Allons, juste pour le fun.
En fait, on a aussi A = A -1, donc A = -1/2 donc 1/2 = – 1/2, donc 1 = 0, cqfd
Mais non, si A = – 1/2 il faut remplacer A par -1/2,ce qui donne -1/2 = -1/2
:p
Voir avec profit tout ce qui concerne la méthode de sommation de Ramanujan…
Koltrane
Voir aussi l’histoire de la série de Grandi :
http://en.wikipedia.org/wiki/History_of_Grandi%27s_series
Bonjour,
En tant que mathématicien, je ne suis pas d’accord avec l’affirmation que « quelle que soit la manière dont on s’y prend, si on veut affecter une valeur finie à cette somme monstrueuse, alors -1/12 est l’unique valeur qui colle ».
Voici en effet un contre-exemple. Par convergence d’Abel (les calculs sont un peu longuets mais valides), on peut démontrer que
-1/2 -2/2 +3 -4/2 -5/2 +6 -7/2 -8/2 +9 -10/2 -11/2 + 12- … = -1/3.
En ajoutant alors terme à teme le double de la série ci-dessus à notre série S, deux termes sur trois se simplifient et on trouve que
S – 2/3 = 3 + 6 + 9 + 12 + … = 3S,
d’où S = -1/3 ≠ -1/12.
De manière générale, dès lors qu’on admet les axiomes de linéarité de la sommation et d’invariance par ajout d’un terme initial nul (axiomes qui ont été utilisés par l’auteur pour établir l’égalité « S = -1/12 »), on voit qu’aucune valeur finie n’est cohérente pour S, car la somme terme à terme
(1+2+3+4+…) – 2*(0+1+2+3+4+…) + (0+0+1+2+3+4+…)
donne d’une part 1+0+0+0+… = 1, et d’autre part S-2S+S = 0, ce qui est contradictoire.
Ma conclusion de mathématicien est donc qu’il n’existe aucune méthode “propre” de sommation de séries divergentes qui permette de donner une valeur finie à S, et que la valeur -1/12 n’est pas plus respectable qu’une autre comme -1/3.
Pour finir, je pense pertinent de souligner que l’auteur a utilisé sans le dire un autre axiome que la linéarité et l’invariance par ajout d’un zéro initial dans son calcul : il a en effet fait usage de la simplification
0 + a_1 + 0 + a_2 + 0 + a_3 + … = a_1 + a_2 + a_3 + …
(j’ai utilisé la même simplification dans mon calcul pour trouver S = -1/3, mais en ne prenant qu’un terme sur trois au lieu d’un terme sur deux). Or, sauf erreur de ma part, si on s’était interdit cet axiome, on ne serait jamais arrivé à trouver de valeur finie pour la somme S : on peut donc dire que c’est en substance cet axiome qui fiche la pagaille ! 😉
Amicalement.
P-S.: Merci pour les très intéressantes applications en physique, que j’ignorais totalement ! 😀
Ce post est d’une stupidité aberrante.
J’ai ri de ces prétendues « démonstrations » rigoureuses ^^
Par exemple, dès l’échauffement 1 : la suite (-1)^n ne tend pas vers 0 lorsque n tend vers l’infini, ce qui fait qu’il est strictement impossible de trouver une valeur finie pour la série des (-1)^n.
Je suis quand même épaté par un truc. Que l’on lise le billet, qu’on décide au milieu que s’est n’importe quoi, et qu’on passe son chemin, ça ne me choque pas du tout (c’est le signe que mon billet est mal écrit).
Mais qu’on fasse l’effort de poster un commentaire pour dire que c’est n’importe quoi, sans avoir lu le billet en entier (ce qui est manifestement le cas des deux derniers commentaires), je ne pige pas.
Alors ok, ce billet est probablement mal organisé et je vais peut être faire une correction pour parler des justifications rigoureuses plus tôt dans l’exposé, mais il me semble que c’est assez clair dans le « pour aller plus loin » que ces sommes généralisées existent bel et bien, que leur définition est tout à faire rigoureuse (et étend le concept de série simplement convergente) et qu’elles sont utilisées par les mathématiciens et même par les physiciens.
Bonsoir,
J’ai quelques éléments mathématiques et physiques en relation avec l’article qui me semblent intéressants:
Lorsqu’on effectue ce prolongement analytique, me viennent à l’esprit les sphères de Riemann ou l’on ramène à zéro l’infini, et dans les diverses methodes de prolongement, l’essentiel est la definition de cette infini, le modulo tel qu’il est mentionné dans l’article. Et le plus naturel à mes yeux est l’intégrale de x, qui correspond finalement à tout les prolongements présentés (mais il en exite d’autres qui amènent a des resultats différentes). C’est pour ca que le résultats négatifs de cette somme n’est pas choquant, car cette serie est inférieure a l’infini pris comme référence dans le prologement.
Pour faire un autre lien avec la physique: dans les systèmes a énergie bornée (dans le modèle) comme une système de spins sur un reseau ou on néglige l’agitation thermique, on a la possibilité d’acceder a des températures négatives qui sont plus chaudes que les temperature maximums. Lorsqu’on dépasse l’infini, on devient négatif… On peut l’accepter avec l’idee de la modulation.
Bien a vous
Manu
Ce qui est dommage dans ce post, c’est pas tant ce que vous en dites, mais plus ce qu’on en retient. On en retient que les mathématiques sont conditionnées ; et en cela, elles sont restrictives. On ne peut lutter contre une ineptie que par un contre-exemple.
Pouvez-vous trouver la valeur de cette suite numérique ? : (7+81+23+14+12000+45+…). Je confirme qu’il s’agit bien d’une somme infinie et que les chiffres se succèdent de façon aléatoire. Vous ne pouvez pas, n’est-ce pas ? Votre échec patent prouve que ne peut pas tout mathématiser ; et du même coup, redonne ses lettres de noblesse à ma définition première : « l’infini qui par définition signifie : « Qu’on ne peut évaluer, qui est incalculable. »
Bien à vous…
Pingback: Weekly links for June 3 | God plays dice
Pingback: Somewhere else, part 58 | Freakonometrics
On a aussi S + A = 2 + 1 + 4 + 3 + 6 – 5 + … = S, soit A = 0 et B = 1/2, S = -1/6 … et D=10
… ou S est infinie et A vaut n’importe quoi….
A = 0 et 1, c’est aussi la solution de A = 1 – A, est plus acceptable intuitivement
N’importe quoi ! Du folklore !
Si le terme général n de la série tend vers l’infinie alors la série de terme générale tend vers l’infinie par nécessité donc ne peut être égale à – 1/12. Ce n’est pas de la science étonnante ce sont des pseudo-démonstration menées n’importe comment !
beh, somme des termes positives !! , normalement c positive :(, et même si on utilise la formule des suite arithmétique on fait tendre le N vers l’infini ,et ça donne l’infini :p, Meme ça reste genial :p comme nouveau idee
Bonjour, l’égalité « choquante » est en fait très profonde : il s’agit en fait de la valeur en s=-1 de la fonction zeta de Riemann. Pour k supérieur ou égal à 2, zeta(1-k) est égal à -B(k)/k, où B(k) est le k-ième nombre de Bernoulli. Pour k=2, on retrouve zeta(-1), la somme des entiers, égale à -1/12. Pour k=3, on trouve zeta(-2), la somme des carrés des entiers, égale à 0. Pour k=4, la somme des cubes des entiers, égale à 1/120…
Reste à justifier qu’un tel « prolongement » de la fonction zeta est possible pour des valeurs réelles négatives de la variable s. Mais les mathématiciens l’ont fait!
« Insupportable » et passionnant. Merci pour cet article et pour le commentaire ci-dessus qui ouvrent une fenêtre sur d’autres mondes. Si cela peut aider: http://en.wikipedia.org/wiki/1_%2B_2_%2B_3_%2B_4_%2B_%C2%B7%C2%B7%C2%B7.
Super article !
Je suis troublé par le fait que l’on cherche à construire des sommations, au lieu de chercher à étendre leur définition en utilisant des règles de manipulation des séries telles que celles que vous utilisez. N’est-il pas possible de montrer que, moyennant certaines règles comme la linéarité et l’ajout de zéros dans les séries, il existe une unique sommation naturelle pour toutes les séries que l’on peut obtenir avec ces règles ?
Ceci justifierait bien mieux à mes yeux le résultat 1+2+3+4+… = -1/12 que des sommations de Césaro, qui paraissent encore trop restrictives, ou des techniques de prolongement analytique, dont on peut avoir l’impression qu’ils donnent un résultat arbitraire.
Tout juste, c’est bien ça qui se passe. On cherche un opérateur S agissant sur l’espace des suites qui soit :
* linéaire
* stable par ajout d’un nombre fini de zéro en début de la suite
* coincidant avec la définition usuelle pour les séries absolument convergentes.
SI on suppose que cet opérateur existe ALORS les manipulations un peu heuristiques que je fais dans le billet sont licites, et on trouve que -1/12 est la seule valeur possible pour 1+2+3+4+…mais il faut encore prouver que l’opérateur existe (sur certaines suites du moins), d’où l’intérêt des approches type Cesaro ou prolongement analytique.
Mon entorse principale, c’est que je fais ces manipulations sans avoir au préalable prouvé que le prolongement existe sur les suites considérées.
Arg… il faut que je repose ma question.
Quelle est la relation entre l’ensemble des séries que l’on peut obtenir avec des manipulations comme les vôtres et l’ensemble des séries que l’on peut calculer par prolongement analytique (ou autre) ?
Depuis hier, j’ai lu quelques autres ressources, mais je n’ai pas trouvé de réponse claire. Wikipédia (en anglais) évoque le théorème de Hahn-Banach pour justifier l’existence d’extension, mais seulement pour les séries à termes bornés. Et, apparemment, cette extension n’est pas unique. Pire encore, il évoque l’axiome du choix et n’est donc pas constructif… Pourtant vos opérations sont très constructives pour calculer la somme (et à résultat unique ?). Bref, je suis un peu perdu et pas convaincu par les explications que j’ai trouvées.
PS: Pour votre calcul de S, il me semble nécessaire de rajouter un nombre infini de zéros (pour tous les indices impairs). Qu’en dites-vous ?
Pour autant que je sache, ca n’est pas prouvé que l’on puisse étendre l’opérateur « Sigma » à toute suite réelle. Encore une fois les opérations de manipulation « heuristiques » ne sont valides que si on a d’abord prouvé que le prolongement existe sur la suite que l’on veut sommer.
J’imagine donc qu’il est envisageable que les manipulations heuristiques puissent donner les résultats contradictoires si on les applique à des suites pour lesquelles il n’existe pas de prolongement de « Sigma ».
En conclusion : si il existe un prolongement (ayant les propriétés susmentionnées), les manipulations sont licites et donnent le « seul » résultat possible. Si le prolongement n’existe pas, on peut envisager que les manipulations heuristiques donnent n’importe quoi !
Mais je n’ai pas d’exemple de suite non-sommable
Effectivement l’article wikipedia (http://en.wikipedia.org/wiki/Divergent_series) en parle.
(et en effet il semble que mon calcul de la somme S ne respecte pas la condition dite de « stabilité »…il faut que je creuse !)
Décidément, votre billet m’aura fait beaucoup cogité ! Je vous en remercie infiniment, et j’espère que mes remarques incessantes ne vous ennuient pas trop. J’ai un peu plus formalisé le fond de ma pensée…
Notons C l’ensemble des suites dont la série converge au sens usuel. C’est un espace vectoriel sur lequel la sommation classique S est bien définie et est linéaire.
Considérons maintenant l’ensemble E des applications linéaires qui insèrent des zéros à une suite, possiblement en nombre infini, tant qu’il reste une infinité de cases pour les termes de la suite initiale (ceci peut être affaibli au besoin). Il me semble à peu près clair que E forme une famille libre de l’espace vectoriel L(R^N) des applications linéaires sur les suites. Maintenant, considérons F l’espace vectoriel engendré par E, dont E est donc une base.
Définissons au passage la forme linéaire l sur F, définie par l(e)=1 pour tout élément e de E. Pour toute suite c dans C, on a S(e(c)) = S(c). On en déduit alors que, si f appartient à F, alors S(f(c)) = l(f) S(c).
Venons-en aux opérations algébriques de votre billet. Étant donné une suite réelle u, les opérations que vous faites consistent à chercher une application linéaire f dans F telle que f(u) soit dans C. L’extension T de la sommation classique S se doit alors de vérifier S(f(u)) = l(f) T(u). Voilà qui pose plusieurs problèmes…
Le premier est qu’il n’est pas dit que toute suite réelle peut être transformée en une suite dont la série converge par une application f dans F. De plus, les cas où l(f) est nul ne nous intéressent pas (quoique… encore faut-il que l’on ait alors S(f(u))=0 !). Qu’importe, on peut essayer d’étendre T à l’union des f^{-1}(C) pour f dans F-ker l. Mais cette union est-elle un espace vectoriel ? Quelle est la taille de cette union, comparée à l’espace des suites sommables par prolongement analytique ?
Le deuxième problème est plus embêtant. Il existe plusieurs f dans F tels que f(u) appartienne à C (si e est dans E, alors e(f(u)) est dans C aussi). En fait, étant donné u, l’ensemble F_u des f tels que f(u) soit dans C est un sous-espace vectoriel de F. Mais, pour pouvoir définir T(u), il faut alors absolument que, si l(f) est non nul, la quantité S(f(u)) / l(f) ne dépende pas du f choisi dans F_u… Hummm…. Est-ce vrai ? Aurait-on pu trouver une autre valeur aux séries de l’article avec une autre manipulation f’ des termes de la série ? Quid de si on se restreint aux images réciproques de l’ensemble des suites nulles presque partout comme c’est le cas dans le billet ? Quid de si on se restreint aux ajouts finis de zéros ?
Bref, ça fait beaucoup de questions, et j’aimerais bien savoir si les réponses existent déjà…
Mmmhhh, miam ! Je ne suis pas sûr d’avoir tout suivi, mais je pense ne pas être d’accord avec l’affirmation
« les opérations que vous faites consistent à chercher une application linéaire f dans F telle que f(u) soit dans C »
Je dirai plutôt que ce qu’on cherche à faire c’est à trouver une application qui :
* soit définie sur un ensemble de suite qui contient C
* soit linéaire
* soit invariante par une application insérant un nombre fini de zéro
* coïncide avec la somme usuelle (convergence simple par la limite des sommes partielles) sur C
La question que je me pose, c’est existe-t-il une telle application qui soit définie sur l’ensemble des suites réelles, ou s’il existent des suites qui ne sont sommables par aucun prolongement de ce genre.
Vu ce que disait wikipédia, je parierais que la plupart des suites réelles ne sont pas sommables, ou du moins, pas de façon unique…
Tiens c’est marrant, tous tes commentaires tombent dans mes spams !
Bonjour David,
J’apprécie beaucoup votre patience et votre rigueur pour répondre aux nombreux commentaires, mais en l’occurrence votre post du 26 juin 2013 à 03:50 est faux ! Car le prolongement que vous évoquez ne peut pas exister sur la somme 1+2+3+… (en revanche, il existe bel et bien sur la somme alternée 1-2+3-4+…). Voir mon commentaire du 1er juin à 13:34 :
– D’une part, vous ne semblez pas vous apercevoir que vous avez utilisé implicitement une hypothèse supplémentaire (à savoir que l’insertion de zéros un terme sur deux ne change pas la somme) ;
– D’autre part, mon post présente un raisonnement analogue au vôtre pour arriver à une somme de -1/3, ce qui met le doigt sur une incohérence ;
– Troisièmement, si on suppose que l’opérateur que vous dites existe (et effectivement un tel opérateur existe bel et bien) (mais il faut enlever l’hypothèse relative à l’insertion de zéros), alors il ne peut pas être défini pour la suite 1+2+3+…, car cela impliquerait en quelques opérations élémentaires compatibles avec les axiomes de S que la somme 1+0+0+… vaudrait 0 !
Bref, je veux bien reconnaitre qu’il existe un moyen canonique d’étendre la notion de somme qui donne -1/12, mais ce n’est pas celui que vous avez présenté (il faut nécessairement passer par la fonction zêta) ; et au final votre article, bien que ne contenant aucune phrase fausse à strictement parler, aboutit à une conclusion erronée : car avec les hypothèses que vous avez faites, il est certes possible de montrer que « la seule valeur possible est -1/12 », mais comme il est aussi possible de montrer que « la seule valeur possible est -1/3 », la vraie conclusion est qu’aucune valeur ne tient la route !
Amicalement,
Tiens effectivement dans le calcul de S j’utilise une hypothèse plus forte que l’insertion d’un nombre fini de zéros en tête de la suite.
Si je comprends votre argument, en appliquant strictement la linéarité et la stabilité par ajout un nombre fini de 0, on peut trouver plusieurs valeurs pour S ?
Ok, ca y est, j’ai pigé l’exemple que tu donnes
»
(1+2+3+4+…) – 2*(0+1+2+3+4+…) + (0+0+1+2+3+4+…)
donne d’une part 1+0+0+0+… = 1, et d’autre part S-2S+S = 0, ce qui est contradictoire.
»
Effectivement, ca répond donc à la question : il existe des suites qui ne sont sommable par aucun moyen respectant les propriétés de linéarité et régularité, et celle-ci en est une.
Mais du coup j’en perd mon latin :
* pourquoi la méthode par le prolongement analytique ne tombe pas sous le coup du raisonnement que tu donnes en exemple ?
* pourquoi effectivement le -1/12 du prolongement analytique de la fonction zeta serait-il plus respectable qu’un autre ? (et donc pourquoi c’est celui-ci qu’on utilise en physique ??)
Bonjour David,
Concernant vos dernières questions, je dois avouer mon ignorance… En ce qui concerne l’application à la physique, j’aurais envie de dire que la « bonne » explication de la valeur -1/12 est l’argument de renormalisation que vous donnez en fin de texte (consistant à retrancher un infini qui était en fait sous-entendu dans les calculs). Cela dit, il n’en reste pas moins troublant que la méthode imaginée par Euler (celle que vous présentez en début de texte), la fonction zêta et la renormalisation aboutissent toutes les trois au même résultat, quand bien même cette valeur n’est pas cohérente avec les axiomes “naturels” sur la somme des séries divergentes… Tout cela suggère qu’il existe une méthode de sommation des séries divergentes “canonique” qui permettrait d’associer -1/12 à la série 1+2+3+…, mais… laquelle ?!
La vérité est que je n’en sais rien. Si une telle méthode existe, elle passe très certainement par du prolongement méromorphe (c’est juste un “gros mot” un peu plus précis que « analytique »), car je ne connais guère d’autre argument pour dire qu’une somme de choses positives pourrait être négative. Mais je ne sais pas quelle règle de plongement méromorphe pourrait être considérée comme canonique sans pour autant vérifier les axiomes naturels (mais tout en les respectant “quand même assez” pour que le calcul d’Euler fonctionne :-/ )… Là, c’est pour moi mystère et boule de gomme !! Au niveau des maths que je connais, j’en suis resté au prolongement d’Abel (éventuellement en passant par le prolongement méromorphe pour dire par exemple que 1+2+4+8+… = -1), mais ce prolongement vérifie tous les axiomes naturels, et ne permet donc en aucun cas de sommer 1+2+3+… 🙁
Amicalement,
Rémi
P-S.: Tant qu’à étaler mon ignorance, j’en profite pour signaler que tout mon baratin sur l’insertion d’un zéro entre chaque terme était en fait hors-sujet, car il se trouve la sommation d’Abel vérifie aussi cet axiome… Le fait qu’aucun opérateur S ne puisse donner de valeur finie à 1+2+3+… n’a en réalité rien à voir avec ça, contrairement à ce que je croyais. (Le seul lien, ce serait que si on enlève l’axiome d’insertion des zéros, j’ai l’impression qu’on n’arrive plus “suggérer” quelque valeur que ce soit pour cette somme — sauf du point de vue strictement logique, à partir du moment où on montre qu’aucune valeur finie n’est possible, on peut en déduire formellement que « la seule valeur finie possible est √22 » [ou toute autre valeur], donc du coup dire qu’on ne peut plus rien suggérer n’est pas très juste…).
Ok je pense que j’y voir plus clair.
Ce que l’on cherche, c’est un opérateur linéaire « somme généralisée », agissant sur un sous-ensemble de l’espace des suites réelles, et qui sur l’espace des séries simplement convergentes coïncide avec la sommation usuelle (la limite de la suite des sommes partielles).
A priori, rien ne garantit qu’un tel opérateur soit unique. Néanmoins, si on ajoute comme condition que l’extension soit « régulière » (ie stable par insertion d’un zéro en tête de série ou bien – je crois que c’est équivalent – par le fait d’isoler le premier terme), alors (sous réserve de l’existence) les manipulations « heuristiques » deviennent licites et imposent une valeur unique à certaines séries, comme 1-1+1-1 ou 1-2+3-4+…
Clairement grâce à ton raisonnement par l’absurde, tout opérateur satisfaisant ces conditions ne peut pas être définit sur 1+2+3+4+5+…
Je me demandais comment c’était compatible avec l’existence de la sommation par la fonction zeta pour 1+2+3+4+… Je crois que la réponse est que cette méthode de sommation n’est PAS une extension de la méthode usuelle, car elle est réservée à la sommation des suites de la forme a_n = n^S. Donc elle n’est définie que sur un sous-ensemble très restreint de l’ensemble des suites réelles. Je pense que ça résout mon interrogation.
Maintenant, mon autre interrogation c’est « existe-t-il d’autres manières de sommer 1+2+3+4+… qui donnent une valeur autre que -1/12 ». A ce jour je n’en connais pas ! Ta méthode pour trouver -1/3 étant illicite (comme la mienne), ça ne compte pas. A noter que la somme de Ramanujan donne aussi -1/12, mais je crois qu’elle non plus ne vérifie pas les « axiomes », en particulier je ne suis pas sûre qu’elle soit définie et identique à la méthode usuelle sur l’ensemble des séries simplement convergentes.
Les points que j’avance ici se basent sur les résultats de ce document: https://arxiv.org/pdf/0705.1578v2.pdf
Pour répondre à David, oui le calcul peut être rendu rigoureux et c’est pourquoi il donne la bonne valeur et de la bonne façon. Mais malheureusement, il a quand même quelque chose d’arbitraire. Tout cela sera plus clair dans la suite.
La preuve de Matheux montre bien que la suite (1;2;3;4;…) n’est pas SSLSR, mais ça ne prouve absolument pas que les calculs heuristiques sont faux! Au contraire , ils sont en fait vrai. Et on peut les rendre parfaitement rigoureux en s’y prenant bien. La confusion vient du fait que (1;2;3;…) n’est pas SSLSR. Oui c’est vrai. Mais si vous le notez bien, dans le calcul, à aucun moment la stabilité n’est utilisée sur (1;2;3;…). L’erreur (de penser que c’est une erreur) vient du fait que comme on utilise la stabilité pour (1;-1;1;…) et (1;-2;3;-4;…), on pense forcément que l’opérateur doit aussi être stable pour (1;2;3;…), or ce n’est pas du tout nécessaire (et fort heureusement, parce que ça conduirait aux incohérences soulevées par Matheux).
Sisi, regardez bien le calcul, la seule propriété qui est utilisée pour (1;2;3;…) est la simplification de (0;1;0;2;0;3;0;…) à (1;2;3;…). Mézalor me direz-vous, comment justifier la rigueur de ce calcul? C’est là que le document nous fournit en partie la réponse. A la fin de la 3ème partie, il trouve que l’ensemble des suites polynomiales qu’on notera M (les suites P(n), n entier où P est un polynôme à coefficient complexe) est en somme directe avec les sommations maximales (qui existent par Zorn) (en gros). Notons qu’il appelle « sommation » une application linéaire et stable (à proprement parler une condition un peu plus faible que la stabilité).
Or justement, (1;2;3…) est une suite polynomiale (le polynôme est X+1). Donc pour définir une Suprasommation (une sommation encore plus grosse que celles qui sont maximales, car elle sera définie sur toutes les suites complexes), il suffit de considérer une sommation maximale (régulière de préférence…) qu’on appellera S1 de domaine H et de considérer une forme linéaire S2 sur M (facilement définissable, car on a une base algébrique évidente de M; par exemple les ((X+1)^k )(n); k parcourant les entiers naturels ). Cette Suprasommation S sera définie sur H+M (somme directe) = C^IN comme suit: Pour tout x dans C^IN, x s’écrit de manière unique x= y + P où y est dans H et P dans M et S(x)= S1(y) + S2(P).
On a bien une « somme » définie pour toute suite complexe car comme l’indique le Théorème 1.8 du doc, le soucis de non-sommation venait en fait des suites polynomiales. Celles-ci ne peuvent être compatibles avec la stabilité.
D’ailleurs, S1 est bien SSLSR mais pas S2.
Et pourtant, cela permet quand même de faire le calcul. Avec une telle définition, on a à priori toute une kyrielle de sommations possibles (déjà pour le choix de (S1;H) maximale mais aussi de S2…).
Et c’est là qu’intervient ce qui se cache derrière la simplification mystérieuse: Il existe une unique forme sur M qui est telle que S (quel que soit le choix de S1) soit invariante par la transformation ( P(n) ) ——-> ( 1/2*( 1-(-1)^n)*P((n-1)/2) ) (où autrement dit l’insertion d’un nombre infini de 0 une fois sur 2 en commençant par un 0 pour les suites polynomiales). Cela se démontre aisément par récurrence sur la base des ((X+1)^k)(n), k entiers naturels. Et en fait, toute sommation S= S1+S2, où S2 est la forme voulue, coïncidera avec la sommation de Dirichlet (limite quand s tend vers 0 de Somme des a_n/(n+1)^s) sur les suites polynomiales. A vrai dire, S2 = la sommation de Dirichlet en restriction aux suites polynomiales.
S1 est choisie – régulière si on veut (et sommant A=(1;-1;1;-1…) et B=(1;-2;3;-4;…) ), quoique la régularité n’est même pas nécessaire. Pourquoi ? Parce que A et B sont des séries quasi-exponentielles et n’importe quelle sommation (au sens du document) les sommant leur donne les valeurs trouvées par les calculs heuristiques. D’ailleurs, regardez de plus près ces calculs heuristiques. Vous verrez qu’on utilise à aucun moment la régularité…Le calcul prouve donc que quelle que soit la sommation sommant A (resp B) qui est stable et linéaire (seulement) alors telle valeur est donnée à A (resp B).
Donc S1 étant choisie (arbitrairement), je disais, il n’y a plus qu’une seule Suprasommation qui corresponde au calcul heuristique. Il suffit de prendre l’unique S2 vérifiant la propriété mentionnée plus haut.
Pour rappel, S(x) = S1(y) + S2(P), où x=y+P.
C’est parti pour le calcul!
S(A) = S1(A) = 1/2 car A appartient à H. S(B) = S1(B) = 1/4 car B appartient à H.
(A et B, en tant que séries quasi-exponentielles, appartiennent à n’importe quel H maximal ; Corollaire 3.6 du doc).
On a trouvé S1(B) = 1/4 car S1(B) = 1 – S1(B) – S1(A).
On note T = (1;2;3…) et T’ = (0;1;0;2;0;3;0;…).
On décide donc de sommer x = T – B.
S(x) = S( T – B) = S2(T) – S1(B), par unicité de la décomposition de x et linéarité de S1 (car T appartient à M et B appartient à H).
Mais x = 4T’, donc 4S(T’) = S(x) = S2(T) – S1(B).
Or comme on l’a dit, S2 a justement été choisie telle que S(T’) = S(T) (T est une suite polynomiale). Il vient donc 4S(T) = S(T) – 1/4. Soit S(T) = -1/12. CQFD
Et le calcul est parfaitement propre .
Alors évidemment, le choix de la forme sur M qui permet l‘invariance de S par insertion d’un 0 sur deux en commençant par un 0 sur les suites polynomiales parait arbitraire. Je suis d’accord. Rien tel quel dans la définition d’une somme, ne permet de savoir pourquoi ce serait cette forme-là particulièrement qui ferait mériter à S le titre de « généralisation » de la Somme. Mais on a bel et bien prouvé que le calcul est parfaitement licite et que, au moins dans un certain sens, 1+2+3+4+….= -1/12. Cependant pour peu qu’on choisisse les valeurs de S2 différemment (en posant des valeurs différentes aux éléments de la base de M), on obtient une autre forme linéaire S =S1+S2, où S1 est linéaire, stable (et régulière si on veut) qui en soi pourrait tout autant mériter le statut de « généralisation » de la notion de somme mais donnerait une valeur différente à (1;2;3;4;….).
Ainsi le choix des valeurs de S2 sur une base de M détermine quelle sommation (et donc quelle valeur) on obtiendra pour toute suite qui contient une partie polynomiale.
Cordialement
Alors petite précision à propos de ce que je dis juste au dessus. Sur deux points.
Déjà le premier est que, pour être valide, le calcul n’a même pas besoin de supposer une propriété aussi forte que celle que j’ai mise (la simplification des 0 qui sont distribué une fois sur deux en débutant par un 0, cette simplification étant valide pour toutes les suites polynomiales). En fait, dans l’absolu, la véracité du calcul de David peut être légitimée simplement en supposant que cette simplification peut se faire pour la suite (0;1;0;2;0;3;0;4;0;5;0;….), ce qui donnera pour valeur -1/12. Mais supposer juste que l’opérateur se simplifie pour cette suite-là semble un tantinet artificiel. Quoiqu’il en soit, c’est mathématiquement juste. La valeur d’une telle somme (comme définie dans le précédent commentaire) sur la suite des entiers vaut -1/12 si et seulement elle peut se simplifier de S(0;1;0;2;0;3;0;4;0;5;0;….) à S(1;2;3;4;5;…); puisqu’on a justement la relation (qui vaut quel que soit la somme S):
4S(0;1;0;2;0;3;0;4;0;5;0;….) = S(1;2;3;4;5;…) – 1/4.
Le deuxième point, rejoignant le premier, est que je disais que rien ne légitime plus cette forme là ( la forme S2 définie sur les suites polynomiales et vérifiant la propriété d’invariance pour toutes ces suites) comme étant la généralisation de la somme. Or, justement, il me semble qu’une caractéristique raisonnable attendue d’une « somme » serait justement une invariance par insertion de 0 de ce type (oui je reconnais que même à supposer cela, ce ne serait pas la seule légitime). Pourquoi je dis ça? Bah la convergence classique des séries est invariante par insertion quelconque de 0 (en nombre fini ou infini). Et on a séparé notre espace C^IN en la somme directe H+M. Or l’opérateur S est invariant par insertion d’un 0 en tête de suite pour H. Il me parait donc « raisonnable » et « légitime » d’exiger une certaine propriété d’invariance (par insertion de 0) pour l’espace M.
Pourquoi nécessairement celle que j’ai présentée? Je n’en sais absolument rien, mais c’est l’idée. Evidemment ce dernier point n’est qu’encore que trop subjectif. Chacun peut émettre son avis sur les propriétés à choisir pour parler de « Somme » avec un grand S (comprendre définie sur l’espace entier des suites complexes). Mais, on a quand même bien avancé non? 😉
A la rigueur, il faudrait peut être plus étudier cette forme S2 pour en faire apparaître des caractéristiques qui la rendraient encore plus « légitime ». Wait and see…
Plus ça va et moins je comprends… Donc la somme S=1+2+3+4+… vaut -1/12 par prolongement analytique, mais ne satisfait pas les axiomes de l’article car S-2(0+S)+(0+0+S)=1. Est-ce que ça veut dire que les séries obtenues par prolongement analytique ne satisfont pas les axiomes de l’article ?
Dans ce cas, le calcul T=1+2+4+8+… par 2(0+T)-T = -1 est-il justifiable ?
Oui je pense que c’est ça. La sommation par la fonction de zeta ne satisfait pas aux « axiomes », car ça n’est PAS une extension de la somme usuelle, la raison en est que la sommation par fonction zeta est définie sur un domaine beaucoup plus restreint que la sommation usuelle.
J’ai compris pourquoi les axiomes marchent pour les séries géométriques divergentes (à l’exception de 1+1+1+1+…), et pourquoi ça n’a que très peu de chance de marcher pour la plupart des autres séries divergentes!
J’ai écrit l’article suivant qui explique les choses en détail : http://www.science4all.org/le-nguyen-hoang/infinite-series/
Chouette article ! J’aime bien le terme de « super-sommation » 🙂
Bonjour,
J’avais abandonné la discussion avec David en cours de route, un peu par paresse, et aussi parce que je ne me sentais pas compétent sur la sommation de Ramanujan (que je ne connaissais pas)… Mais comme la question de “Lê” est cette fois-ci dans mes cordes, et qu’en plus je reconnais en lui l’aimable récent commentateur d’un de mes articles de vulgarisation (intitulé « Et le v*** »), je reviens autour de la table !
Généralement, quand on parle de définir la somme a_0 + a_1 + a_2 + … (où les a_i sont supposés croitre moins vite qu’une certaine exponentielle) par prolongement analytique, on s’intéresse au prolongement analytique de la fonction f(z) := a_0 + a_1 z + a_2 z^2 + …, en espérant qu’un tel prolongement analytique soit défini pour z = 1.
Même ainsi, il y a plusieurs manières de dire ce que signifie l’existence d’un prolongement analytique :
* Par exemple, on peut juste se demander si, à défaut de converger pour z = 1, la série ne converge pas pour des valeurs arbitrairement proches de 1, et regarder le cas échéant s’il y a une limite quand z tend vers 1 (si je ne dis pas d’âneries, cela redonne notamment la somme habituelle de toutes les séries semi-convergentes [comme 1 – 1/2 + 1/3 – 1/4 + …] ; et cela donne aussi que 1 – 2 + 3 – 4 + … = 1/4).
* On peut aussi regarder s’il existe un prolongement analytique de f sur un intervalle de R qui contienne [0,1] (auquel cas ce prolongement est nécessairement unique) : par exemple, on trouve par cette méthode (sauf erreur de calcul) que 1 – 1/1 + 1/1 * 3/2 – 1/1 * 3/2 * 5/3 + 1/1 * 3/2 * 5/3 * 7/4 – … vaut racine carrée de (1/3) [la fonction f(z) étant alors “1/racine(1+2z)”].
* Au niveau supérieur, on peut regarder s’il n’existe pas un prolongement analytique dans C, ou plus exactement dans un certain sous-ensemble ouvert U de C. Mais là, attention, car la même somme peut recevoir des valeurs différentes en fonction du choix de U ! Ainsi, sur la somme que j’ai donnée tout-à-l’heure, en choisissant un U un peu retors, on pourrait trouver pour somme -racine(1/3). Du coup, cette méthode est un peu décevante, car on perd la “canonicité”…
* Enfin, on peut décider de ne considérer que les cas où le résultat trouvé avec cette méthode de prolongement complexe est indépendant du choix de U : c’est en particulier le cas s’il existe ce qu’on appelle un « prolongement méromorphe » de f. Avec cette méthode, on obtient par exemple que 1 + 2 + 4 + 8 + … = -1.
Toutes ces méthodes vérifient les axiomes que nous avons listés ci-dessus (à quelques nuances près en ce qui concerne la troisième méthode proposée, mais passons), et ont donc, sans surprise, toutes comme point commun de ne pas savoir donner de valeur à 1 + 2 + 3 + 4 + … — et même pire : elles disent que cela correspond à un point intrinsèquement divergent.
MAIS le prolongement par la fonction zêta (qui est lui défini pour la somme des entiers et donne alors -1/12) ne repose pas sur le prolongement analytique de la fonction f(z), mais sur celui d’une autre fonction ! (il s’agit quand même d’un prolongement analytique ; et du prolongement analytique d’une fonction qui redonne formellement la série des entiers pour le bon choix de z ; mais ce n’est juste pas f(z) qu’on a choisi de prolonger, mais quelque chose de plus compliqué — appelons cette autre fonction qu’on prolonge ‘g’). Et, pour ce qu’il m’en semble, la fonction g en question est une espèce de bricolage “ad hoc” qui marche bien pour la somme des entiers naturels, mais dont on ne saurait pas vraiment donner l’analogue pour d’autres séries ! De toutes façons, le fait que la méthode utilisée arrive à donner une valeur à la somme des entiers montre qu’on est dans (au moins) un des deux cas suivants :
* Soit la méthode (à supposer qu’on sache la définir proprement) ne sait pas sommer toutes les séries convergentes, ou donne un résultat qui n’est pas la somme usuelle (par exemple zéro) : cela est l’hypothèse que faisait David ;
* Soit la méthode ne vérifie pas un des autres axiomes [linéarité ou insertion régulière de zéros].
David évoque aussi la sommation de Ramanujan, qui semble à ce que j’en ai vu plus “canonique” que l’idée de la fonction zêta. Puisque cette méthode donne elle aussi une valeur à la somme des entiers, c’est forcément à nouveau qu’une des deux hypothèses ci-dessus a encore lieu pour cette méthode : d’après ce que j’en ai lu, il semblerait que ce soit la première des deux qui explique le bug (les axiomes de linéarité et d’insertion régulière étant, par contre, vérifiés).
Dans tous les cas, ce qui serait intéressant (mais largement au-delà du sujet je crains) serait de décortiquer, aussi bien la méthode de la fonction zêta (à supposer, encore une fois, qu’on sache définir une méthode générale correspondante) que la sommation de Ramanujan, et voir si, en interprétant les calculs de l’article à l’aune de ces méthodes, on peut dire qu’effectivement ceux-ci ont un sens ; ou si ce n’est qu’une coïncidence (qui serait alors stupéfiante !) qu’on retrouve dans les trois cas la valeur de -1/12.
Bien à vous.
Bonjour Rémi,
Merci de faire ce tour d’horizon des méthodes de sommations analytiques. C’est très intéressant ! Ma préférée est la 4ème, mais j’aimerais bien voir la preuve que les axiomes du billet sont satisfaits pour celle-ci :P. Avez-vous un lien vers lequel m’envoyer ?
Au passage, je trouve amusant que la série choisie par David dans ce billet soit la plus complexe et mystérieuse de toute !
Alors, comme ça, j’aurais commenté un de vos articles ? Je n’arrive pas à retrouver lequel ! Vous pourriez mettre un lien s’il vous plaît ? Merci !
Merci belle analyse !
En fait j’ai choisi celle dont je connaissais les applications en physique ! Le fait que ce soit la plus compliqué est justement un peu inquiétant du coup. Est-ce que ce qu’on fait avec en physique est vraiment solide si le résultat dépend de la méthode de sommation (et que rien ne préscrit cette méthode dans le problème physique) ?
C’est faux. Les calculs ont beau être bons, vous considérez S= 1+2+3+4+5+…., ce qui suppose que S existe et à une valeur finie. Or, comme on me le rabâche sans arrêt en master de Maths, il est interdit d’écrire qu’une telle somme à une valeur sans vérifier qu’elle converge. Et votre somme ne converge pas.
Voilà pourquoi le résultat paraît si improbable. C’est vrai qu’en maths, si on ne respecte pas tout, on peut démontrer tout et n’importe quoi (surtout en passant par des lettres). Par exemple, je connais une démonstration qui montre que 1+1=3. Lorsqu’on arrive à des valeurs aussi vraisemblablement illogiques (une somme de nombres positifs ne peut pas donner un nombre négatif), c’est qu’il y a une erreur mathématique quelque part.
D’ailleurs, c’est pareil pour votre A et votre B. Les sommes infinies ne convergent pas, donc n’ont pas de limite, et donc A et B n’existent tout simplement pas.
Je vous invite à lire l’intégralité du billet, ainsi que l’ensemble des discussions en commentaire, qui je pense répondent largement à vos craintes.
Dans le cas contraire, je vous renvoie au livre « Divergent series » du mathématicien G.Hardy, ou encore aux nombreux écrits sur le sujet des chercheurs en mathématiques, comme par exemple celui-ci :
http://math.arizona.edu/~cais/Papers/Expos/div.pdf
En espérant que cela vous convaincra que tout cela est un véritable sujet de recherche sérieux, et pas juste mes élucubrations personelles délirantes !
J’aurais dû être plus précise: cela n’est pas possible dans les maths usuelles. Une série divergente n’a pas vraiment de somme. En revanche, si l’on décide de faire abstraction de cette interdiction, on peut tout à fait calculer ces sommes et trouver des valeurs comme vous l’avez fait. Je suppose que c’est l’apparente absurdité de ces valeurs qui a fait que les mathématiciens (je dis « les », mais je sais bien que ce n’est pas le cas de tous) ont interdit ces calculs.
Bref, si on décide de donner quand même une valeur à ces sommes, on part alors dans une autre forme de mathématiques. Ce n’est donc pas faux au sens absolu du terme, c’est juste faux au sens des mathématiques usuelles, que l’on apprend au collège – lycée – fac. Si j’avais mis un truc pareil dans mes copies d’exam, je me serais faite engueuler ^^
Après, je ne nie pas que cette étude a de l’intérêt. Les résultats obtenus par des mathématiques « annexes » peuvent toujours être utilisés dans la vie réelle, ce que je trouve assez fascinant.
Tout dépend de la façon dont on décide de définir une série divergente, en fait. Mais ça va plus loin que ça: si on admet que S=-1/12, on admet que la somme de nombres positif peut être négative, et cela étend énormément les possibilités. À partir de cette seule décision, on peut recréer un univers mathématique différend de celui dont on a l’habitude, qui donne des résultats qui peuvent à priori paraître absurde, mais qui fonctionnent tout de même si on les applique en physique, par exemple. Je trouve ça à la fois fascinant et inquiétant, parce que ça veut dire que les règles ne sont pas les même en fonction du contexte dans lequel on les applique.
Comme quelqu’un l’a dit dans un commentaire, si on me donne 1€, puis 2€, puis 3€, etc, il est impossible que j’ai perdu de l’argent, au final. Et pourtant, dans un autre contexte, ce résultat fonctionne.
Ouai non mais si on travaille avec des séries divergentes on peut prouver ce qu’on veut, comme il a été dit plus haut 0=1, on manipule des choses qui n’existent pas et puis tadaaaaa!
Cependant ceci reste intéréssant et même Euler avait remarqué ses égalités paradoxales : http://fr.wikipedia.org/wiki/S%C3%A9rie_altern%C3%A9e_des_entiers
Manipuler A comme si c’était un nombre suppose que la somme 1-1+1-1+…. est finie, ce qui n’est pas le cas. A partir de là on aurait pu la rendre égale à n’importe quoi.
Je comprends qu »au sens des séries divergentes » tu obtiens ton résultat, mais il aurait fallu l’écrire quelque part au moins… Car là tu fais croire que c’est vrai au sens usuel, c’est un peu too much.
Après avoir lu l’article en entier, enfin pour la partie maths. Je reconnais que ça a du sens si on étend l’opérateur, et là ça commence à être très intéressant
La première question que je me suis posée était « quand est-ce que le signe bascule »?
En effet pour sum k on a du négatif, mais on du positif pour des quantités comme 1-1+1-1+… Je suis curieux de connaitre le noyau de T, ou quelques propriétés sur T. Je vais regarder vos références.
Je vois que bien du monde s’est amusé avec cet article alors je saute aussi dans la coure d’école et je propose la suite Z= 1+1+1+….il vient:
Z+A=2+2+2+…..
Z+A=2Z
Z=A d’où Z=1/2
C+Z= 2+3+4+5+…
C+Z=C-1
Z= -1
Alors que vaut Z? 1/2 ou -1 ou n’importe quoi!
Merci pour ce divertissement qui m’a beaucoup interpellé et beaucoup diverti.
Pingback: The Surprising Flavor of Infinite Series - S4A
Je coince dès la première série ; la démonstration pour A=1/2 n’est pas pour moi rigoureuse: si l’on écrit A= a1-a2+a3-a4+.. avec les a indice i=1, alors A= 1-(a2-a3+a4-..) et pour moi , le terme entre parenthèses n’est pas strictement identique à A mais à -A+1;et on l’on peut alors conclure que A=A
D.P.
Salut,
Des termes positifs croissants qui donnent un nombre inférieur à 1, on m’explique ?
Déjà faut arrêter de raisonner en faisant une équation « normale » alors qu’on a une partie quasi-inexistante de l’opération, pour moi une opération comme ça ne peut pas être résolue par des équations mathématiques utilisées habituellement.
J’ai l’impression que vous essayez de calculer la taille de l’univers avec des baby-foot.
Enfin si quelqu’un est capable de m’expliquer, j’attends que ça.
Dès le début, le titre montre que l’opération (+) n’est pas interne à (ℤ, +), ce qui suffit d’emblée à disqualifier le raisonnement. Depuis le temps, ça finirait par se savoir …
Je dirai simplement que ± ∞ n’appartenant pas à ℤ (ni même à ℝ), A = (+∞) + (-∞) n’a tout simplement pas de sens.
Ensuite, on peut ajouter n’importe quoi à ça : ça ne lui donnera pas plus de sens.
Comme vous y allez, je vous trouve bien sûr de vous 🙂
A moins que vous soyez un super spécialiste de la sommation des séries divergentes, je trouve ça un peu risqué comme attitude !
Allez donc jeter un oeil à ça
http://math.arizona.edu/~cais/Papers/Expos/div.pdf
voir carrément à ça si ça ne vous suffit pas
Divergent series
Non, ce n’est pas ça que montre le titre. Car (+) est une opération binaire qui ne prend que deux arguments et le symbole sigma peut être appelé une opération « infinitaire » et ce n’est pas l’opération (+). Il n’y a aucun théorème qui dit que si tous les termes sont dans Z alors leur « somme » est dans Z (ici le mot somme ne désigne pas l’opération (+) mais plutôt une généralisation de celle-ci qu’on note avec le symbole sigma) et l’écriture a+b+c+d+… n’est qu’une « métaphore » pour désigner que ce nombre là est construit à partir de la loi (+) et ces termes là (a, b, c, d,…) et lorsque la sommation usuelle est utilisée, celui-ci dépend aussi de la distance usuelle sur R, car il est défini comme limite de la suite des sommes partielles de la suite. (les sommes partielles dépendent de la définition de (+), et la limite dépend de la distance utilisée)
Enfin, l’opération qui associe au triplet (a,b,c) la somme a+b+c n’est pas une opération binaire, elle est trinaire et notée en utilisant deux symboles « + » qui séparent les termes. a+b+c est ainsi défini comme étant égal à (a+b)+c qui n’est autre que a+(b+c) dont chaque symbole « + » ici désigne l’opération binaire (+). Et ainsi toutes les sommes finies n-aires (utilisant n-1 symboles « + » qui séparent les termes) sont définies à partir de l’opération binaire. De même, la sommation sigma est définie à partir de l’opération (+) et de la distance pour définir la limite. Il y a d’autres sommations qui sont des généralisations intéressantes de l’addition « finit-aire » et elles sont toutes notées avec le symbole sigma.
Et ce qui vous induit en confusion c’est que la notation a+b+c+d+… n’est qu’une notation heuristique de la sommation qui sous-entend que si on voit les premiers termes écrits, on doit connaitre la suite. La notation formelle n’est autre que le symbole sigma suivi par le terme général en précisant le domaine de la variable et l’ordre suivant lequel on somme.
Veuillez noter que même si on suit votre raisonnement (en supposant que vous reconnaissez que 1+1+1+1… est un nombre infini) on va conclure alors que l’opération (+) n’est pas encore interne à Z.
Et en confondant cette sommation (qui prend une infinité de termes) avec l’opération binaire (qui prend deux termes) en les considérant la même opération donc avec les mêmes propriétés, on doit alors associer à 1+2+3+4+… un nombre dans Z puisque Z est stable par l’addition. Enfin ce raisonnement n’est qu’une confusion.
J’espère que ça vous a aidé à comprendre.
Pingback: Le scandale des séries divergentes ! (ou le retour de 1+2+3+4+5+… = -1/12) | Science étonnante
La formule d’Euler-MacLaurin donnée dans la toute fin de l’article (\sum_n f(n) – \int_0^{+\infty} f(x) dx = \frac{1}{2} f(0) – \frac{1}{12} f'(0) + …) est différente de celle donnée dans wikipedia : \sum_n f(n) – \int_0^{+\infty} f(x) dx = \lim_{x\to \infty} (\frac{1}{2} (f(0)-f(x)) – \frac{1}{12} (f'(0)-f'(x)) + …) ?
J’aurais plus tendance à croire la formule de wikipedia puisqu’il serait étonnant que la différence de ces deux termes ne dépende que du comportement en 0 de f.
Auquel cas on trouverait que le fameux terme en – \frac{1}{12} s’annule et qu’il reste un terme divergent en x/2 et donc plus vraiment de justification de l’utilisation de série divergente.
L’effet casimir s’explique (et d’ailleurs c’en est l’origine) également par les forces de Van der Waals retardées. Apparemment il y aurait une espèce de dualité en électrodynamique quantique. Je me demande si il ne s’agit pas d’une coincidence entre les résultats qu’on obtiendrait avec un calcul de Van der Waals, (qui fait intervenir des 1/r^6, et une intégrale de surface) et le type de divergences qu’on retrouve dans les calculs quantiques dont on parle ici.
j’ai oublié de m’abonner aux commentaires, abonnez moi!!
Article qui me semble plutôt intéressant, dommage que ce soit faux d’entrée !
La somme A n’est pas égale à 1/2 : mettre des points de suspension « à l’infini » n’a pas vraiment de sens, alors faire des calculs avec …. Et comme souvent : faire quelque chose qui n’a pas de sens, conduit à n’importe quoi ….
Donc B est faux, donc S est faux … Vous comprendrez que j’ai pas lu la suite ^^
C’est pas malin de poster un commentaire sans même avoir lu l’article en entier !
Allez donc aussi lire la suite : http://sciencetonnante.wordpress.com/2014/01/20/le-scandale-des-series-divergentes/
On a A qui est divergente, et sa limite vaut 1/2 ?!
Je me répète, mais allez lire ça :
http://sciencetonnante.wordpress.com/2014/01/20/le-scandale-des-series-divergentes/
Ca s’appelle « Le scandale des séries divergentes »
Il serait bon de lire avant de se vanter de ne pas avoir lu… surtout quand on a affaire à un texte de qualité.
@Lê mdr. Du coup ça revient à « il serait bon de manger avant de se plaindre d’avoir faim » ?
Boutade à part, étant comme de juste choqué qu’une somme de positifs puisse être négative, mais assez convaincu par les démarches, je m’interroge tout de même sur 2 points : la précédence des mathématiques sur la physique, et l’impossibilité de coïncidences.
Je m’explique : ne serait-ce pas la nature profondément probabiliste de la mécanique des quanta qui permette un tel résultat ? et n’est-il pas possible que la fréquente apparition du nombre 12 – en mathématiques comme dans la nature – ne soit qu’une coïncidence ? Et si non, pour le 2ème point, cela signifie-t-il quelque chose ?
Cordialement
Bonjour ! Je suis tombé sur cet article par hasard ms après l’avoir lu une question me turlupine -elle peut paraître stupide- : comment avez vous fait pour décomposer le terme entre parenthèses dans l’exemple 2 (somme B) ?
Cordialement
On enlève et on ajoute alternativement 1 à chaque terme de la somme entre parenthèse.
N’importe quoi! L’échauffement niveau 1 démontre également que 0=1, ce que tout le monde sait déjà…
Comment ça?
Soit. S vaut donc -1/12.
En utilisant le même procédé que pour « (1-1+1-…) = 1 – (1-1+1-…) => A = 1/2
(1+2+3+…) = 1 + (2+3+4+…) => (2+3+4+…) = – 1/12 – 1 = -12/13
Et en utilisant le même procédé que pour « (1-2+3-…) = 1 – (1-2+3-…) – (1-1+1-…) => B = 1 – B – A = -1/4 »
(2+3+4+…) – (1+2+3+…) = (1+1+1…) => (1+1+1…) = (2+3+4+…) – (1+2+3+…) = – 1
Et donc
-1 = (1+1+1+…) = 1 + (1+1+1…) = 1 + 1 + (1+1+1…) = 1 + 1 + 1 + (1+1+1…)
Soit -1 = 0 = 1 = 2 = 3…
Et ça y est on est devenu complètement débile…
-13/12
Cette absurdité que vous trouvez montre qu’il n’existe pas de sommation régulière, linéaire et stable suivant laquelle 1+1+1… puisse converger vers un réel.
J’essaye d’être plus clair. Lorsque l’on suppose une assertion P qui s’écrit comme conjonction d’autres assertions (P est équivalente à [A et B et C] ) et qu’on se retrouve face à une contradiction, cela prouve que la proposition P est fausse et non pas que chacune des propositions A, B et C est fausse. P peut être fausse sans que A, B , C ne soient toutes fausses.
Ici vous avez supposé implicitement que la sommation que vous utilisez pour donnez une valeur à 1+1+1… est régulière, stable et linéaire et est la même que celle qui associe la valeur -1/2 à 1+2+3+4…
Donc on en déduit que celle-ci ne peut guerre converger pour 1+1+1… et ce n’est pas débile du tout.
Pingback: Fiches thématiques | Pearltrees
Salut à tous !
On peut en effet dire que 1+2+3+4+5+6+…= -1/12 mais sous certaines conditions comme explicité dans l’article, car en regardant un peu ça paraît étrange !
La fonction zêta « de base » qui est zêta(x) = (Somme de n=0 à l’infini) 1/(n^x) est définie pour les nombres complexes dont la partie réelle est strictement supérieure à 1 car celle ci ne converge pas pour les valeurs inférieures à 1 ! En effet, si x=1 il s’agit de la suite harmonique (qui diverge), et si x prend des valeurs négatives comme -1, on obtient zêta(-1)=(Somme de n=0 à l’infini) 1/(n^-1) =(Somme de n=0 à l’infini) n = 1+2+3+4+5+6+…. on obtient des suites qui divergent ! ( en effet 1+2+3+4+5+…= (n(n+1))/2 qui tend vers l’infini quand n tend vers l’infini).
Alors pourquoi dire que cette fameuse somme égale à -1/12 alors qu’elle est censée être non calculable ? C’est parce que les mathématiciens ont inventé un système pour prolonger le domaine des fonctions, afin de calculer des valeurs qui ne sont normalement pas calculable : il s’agit du prolongement analytique. La fonction zêta « de base » est définie pour touts nombre complexe dont la partie réelle est strictement supérieure à 1, c’est alors que Riemann eût l’idée géniale d’élargir le domaine de cette fonction afin de pouvoir la calculer même pour des valeurs dont la partie réelle est inférieure à 1 ! La fonction zêta a donc été prolongée sur C-{1}, l’ensemble des nombres complexes privé de 1, et cette nouvelle fonction à été baptisée… zêta ! En effet la fonction désignant le prolongement analytique de zêta porte le même nom que celle-ci, d’où pas mal de confusions.
Cette nouvelle fonction est maintenant calculable partout, sauf en 1, car on retombe sur notre série harmonique qui ne converge pas du tout même avec le prolongement analytique (on dit que la fonction possède un pôle simple en 1, en gros elle tend en +ou- l’infini en cette valeur).Grâce à ce prolongement, on peux calculer zêta(-1), qui égal à -1/12 !Cela veut-il dire pour autant que 1+2+3+4+5+6+…= -1/12 ? Eh bien pas ou sens où on l’entend, car la formule de la fonction « de base » (i.e. zêta(x)=(Somme de n=0 à l’infini) 1/(n^x)) n’est qu’une définition possible de la fonction zêta seulement si la partie réelle de x est supérieure à 1 ! Ce n’est cependant pas le cas pour -1, donc on ne peux remplacer x par -1 dans cette formule.
La conclusion à en tiré est que si cette somme monstrueuse devait avoir un résultat, cela serait -1/12 comme dit dans l’article car ce résultat est calculé avec le prolongement analytique, et n’est définie que dans un domaine spécial ! Dire que 1+2+3+4+5+6+…= -1/12 est un peu barbare, mais signifie vulgairement que par prolongement analytique on obtient -1/12. Cette valeur peut paraît bizarre, surtout car elle est négative, mais il s’agit d’une valeur affectée à quelque chose qui normalement ne converge pas, donc quelque soit le résultat c’est bizarre 😉
Pour les calculs avec les sommes je pense qu’il n’y a rien a redire, mais je pense tout de même qu’il y a encore une histoire d’ensemble plus grand,une sorte de prolongement analytique qui rend ce calcul possible. En effet de base la fameuse série A avec la somme des (-1)^n est sensée diverger, car la suite (-1)^n ne tend pas vers 0 donc la série est non convergente (critère de Cauchy me semble). Or la moyenne de Cesaro donne 1/2, il y a un petit problème… Qui je pense peut-être probablement justifiée en posant un ensemble où tout cela est possible ! Ouf c’est enfin terminé ! Merci de m’avoir lu, et bonne continuation à tous !
(Desoler pour les fautes d’accords/accents, j’ecris depuis un clavier qwerty)
Article vraiment interessant, je me suis un peu amuser a chercher d’autre sommes qui pourrait donner ce type de relations et je suis tomber sur quelque chose d’interessant (je ne sais pas si ca a deja ete mentionner quelque part).
On a par exemple la somme suivante:
X = 1 + 2 + 4 + 8 + 16 + 32 + 64 + …
X = 1 + 2(1 + 2 + 4 + 8 + 16 + 32 + 64 + …)
X = 1 + 2X
-X = 1
X = -1
De la meme maniere:
X = 1 + 3 + 9 + 27 + 81 + …
X = 1 + 3(1 + 3 + 9 + 27 + 81 + …)
X = 1 + 3X
-2X = 1
X = -1/2
Ce qui fonctionne avec toutes les puissances d’entiers et donc on peut generaliser de la sorte:
S(n) = n^0 + n^1 + n^2 + n^3 + n^4 + …
S(n) = 1 + n*S(n)
S(n) = 1/(1 – n)
Deux, trois choses interessantes qu’on peut noter de cette formule:
– Pour n = 0 Soit S(0) = 0 + 0 + 0 + 0 + … S(0) = 1
– Pour n = 1 Soit S(1) = 1 + 1 + 1 + 1 + 1 + … On a une division par 0
Ce qui colle avec le fait que cette somme donne des resultats incoherent du type 0 = 1 = 2 = 3 …
– Pour n = -1 Soit S(-1) = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + … On trouve -1/2 Comme avec les autres methodes ( S(-1) = A )
Et ce que je trouve le plus marrant:
– Pour n = 13 On trouve S(13) = -1/12
Soit la meme chose que pour S = 1 + 2 + 3 + 4 + 5 + 6 + …
On a aussi pour n = -3 S(-3) = 1/4 Comme pour la somme B de l’article 1 – 2 + 3 – 4 + 5 – 6 + …
Donc si quelqu’un vois un rapport entre:
S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + …
et
S(13) = 1 + 13 + 169 + 2197 + 28561 + 371293 + 4826809 + …
A part que le nombre de chiffres des termes de S(13) est egale au terme correspondant dans S, mais bon pas sur que ca fonctionne indefiniment (pas verifier…) ca aurait marcher avec 10 par contre …
D’ailleurs il est interessant d’ecrire:
S(10) = 1 + 10 + 100 + 1000 + 10000 + 100000 + … = -0.11111111…
Ou un rapport entre:
B = 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + …
et
S-3 = 1 – 3 + 9 – 27 + 81 – 243 + 729 – 2187 + …
Je trouve ce sujet vraiment interessant, et qu’il doit bien y avoir quelque chose a creuser la derriere mais je ne sais pas trop quoi…
Je pense qu’il serait interessant d’essayer d’exprimer les sommes que l’on utilise avec des formules, comme pour S(n) ci-dessus, plutot que d’utiliser des ecritures « intuitives ».
Voila dite moi si ca vous inspire quelque chose…
Msul pas jcomprend pa
Bonjours à tous,
Il me semble que la formule d’Euler Maclaurin est fausse dans cet article .. si on fait un dessin, on comprend bien pourquoi : la différence entre la somme des entiers et l’intégrale de f(x) = x sur R est sensée être infinie. Officiellement, dans le théorème, il y a un terme f(n)/2 qui apparaît dans l’égalité ; celui ci tend bien sûre vers l’infini lorsque l’on prend la limite en l’infini.
Et pour ce qui est des septiques, il faut arrêter de penser que le symbole somme utilisé pour dire que la somme des entiers est égale à -1/12 est le même que celui des séries entières que l’on nous apprend en math sup…On travail dans un autre espace vectoriel normé que (R,abs(x)) (où abs est la norme usuellement choisit en math sup… n’est-ce pas ;-)) C’est juste un confie de notation (inventez un symbole nouveau si ça vous fait plaisir).
Donc si on me donne 1€ + 2€ + 3€ + 4€ + …. au final je me retrouve avec moins un douzième d’euro ? 🙁
Putain j’ai rigolé xD
Ou comment faire n’importe quoi avec les « maths » pour donner n’importe quoi…
On passe pas d’un référentiel à un autre comme ça, faut des conditions pour que ca ait une espèce de cohérence scientifique.
C’est un plaisir de vous distraire ! N’hésitez pas à revenir sur ce site pour d’autres canulars !
Une cyber-attaque de l’homme de base ?
À mon avis, le raisonnement de la partie « Échauffement, niveau 1 » est erroné à cause du nombre d’éléments différents dans les ensembles. J’ai développé ce point de vue ici : http://www.blueman.name/Des_Videos_Remarquables.php?NumVideo=7851
Pingback: L’incroyable addition 1+2+3+4+…=-1/12 – Micmaths | Soyez curieux
La réponse apportée par les mathématiciens à ce problème est assez simple: c’est une série divergente, donc on ne peut pas calculer sa somme. C’est interdit. D’autant que les démonstration mathématiques se basent parfois sur des énoncés évidents, tels que « la somme de nombres positifs est positive »; dès lors ils ne peuvent accepter un tel résultat sans en fausser de nombreux autres.
Donner une valeur à ces sommes pose un autre problème. Gardons votre démonstration, qui semble correcte à toute personne n’ayant jamais entendu parler de série divergente. Mais, au lieu de faire S-B, voyons ce que donnerais S+A (par pure curiosité):
S+A=(1+2+3+4+5+6++8+…) + (1-1+1-1+1-1+1-1+….)
S+A=2+1+4+3+6+5+8+7+10+9+….
Cela nous redonne, quoique dans le désordre, les termes de S. Donc, S+A=S.
On en déduit que A=0. Ce qui va en contradiction directe avec le fait que A=1/2.
Bref, jouer avec ces sommes est rigolo, mais reste mathématiquement incorrect.
Précisons tout de même que je parle des mathématiques « communes », celles que l’on apprend au collège et que l’on utilise en général; Dans d’autres mathématiques, on pourrait tout à fait admettre ces calculs. Ce qui les rend utilisables en physique, malgré leur apparence illogique. C’est d’ailleurs pour ça que ce n’est pas ce type de mathématiques que l’on apprend au collège… Il existe des tas de formes de mathématiques différentes, en fonction de ce que l’on se pose comme limite. La plupart des mathématiciens décident d’ajouter des règles de calculs quand on tombe sur des trucs apparemment illogiques; d’autres continuent tout de même, parce que le monde qui nous entoure ne respecte pas forcément la même logique que nous.
Donc, pour être précis, je dirais que ce calcul est faux dans les maths « communes », mais peut tout à fait se révéler exact et utile dans d’autres formes de maths. Voilà pourquoi les maths, c’est cool.
Bonjour, je viens de découvrir le billet, et ai un niveau de Bac S, je ne suis donc pas spécialiste.
J’aimerais que l’on m’explique la décomposition de la somme entre parenthèse de la seconde étape, car en regroupant les deux sommes entre parenthèses qui apparaissent à la ligne suivante, je ne trouve pas la même chose. Je pense que quelqu’un s’en serait rendu compte, pourtant j’ai l’impression qu’il y a une erreur de signe et que B = 1- B + A et non B = 1 – B – A.
Merci d’avance.
EDIT : j’ai trouvé mon erreur, c’est moi qui ai oublié de distribuer le signe négatif de la première parenthèse.
Pingback: Sommes entières infinies - Riemann et Casimir – jardin du vide
Pingback: The Surprising Flavor of Infinite Series
Dès le niveau 1 c’est faux. La moyenne sera de 1/n si n est impair, 0 si n est pair. Je ne veux même pas regarder la suite.
C’est bien dommage…car le papier est pédagogique et bien expliqué ! Vous n’avez pas l’air d’être un « spécialiste » de mathématique alors arriver ici avec des gros sabot pour faire l’inverse !
J’ai fait des études de math poussé, et c’est cohérent (moyenant les explication dans l’article d’après)! Non usuel certe, mais les mathématique sont elle toujours usuel? On apprend bien les nombre complexe au lycée, et pourtant, ça n’est pas « usuel » non plus !
Laissez donc de coté votre compréhension « instinctive » de toutes les opérations mathématiques (les « – » et les « + » ne sont pas si anodins que ça), et essayer de comprendre ce qui se cache derrière.
Floflo a raison… C’est n’importe quoi du début à la fin… ça sent le Troll à plein nez!
Je me demande qui peut bien avoir le courage d’écrire un article de cette taille sans même s’assurer de sa cohérence…
Y a des indécrottables dans les commentateurs. Ils ne comprennent pas grand chose mais ilssont persuadés
de detenir leur vérité ! Ah cette nature humaine !
Regarder plutôt The Voice, c est plus à votre portée
Pingback: La théorie des cordes | Science étonnante
Je me permets d’expliquer autrement comment : 1-1+1-1+1-1+1- ….. = 1/2
Si cette suite doit nécessairement se terminer par:
la valeur 1 alors sa somme est 1-1+1-1+1- ….+1 = 1
la valeur -1 alors sa somme est 1-1+1-1+1- …-1 = 0
Et la somme 1-1+1-1+1-1+1- … n’est autre qu’une façon d’envisager ces deux suites à la fois c’est à dire trouver leur moyenne arithmétique qui est égale à 1+0 : 2 = 1/2
Bonjour,
I. Article intéressant
Le fait de ne pas être un super matheux, au début (somme = 1/2), j’ai du mal à suivre :
A = 1 – 1 + 1 – 1 + 1 – … = 1 – (1 – 1 + 1 – 1 + 1 – …)
car on rajoute le terme 1
On aurait pu aussi bien dire :
A = 1 – 1 + 1 – 1 + 1 – … = 1 – (1 – 1 + 1 – 1 + 1 – …) – (1 – 1 + 1 – 1 + 1 – …)
A = 1 – A – A
A = 1/3
J’ai l’impression que ces artifices de calcul ne représentent pas la réalité et qu’on peut faire dire ce qu’on veut.
Je dois me tromper, mais aimerais comprendre.
II. Somme des entiers naturels = -1/12
Mon raisonnement (simple) :
0 +1 + 2 + 3 = 6
à 6 on ajoute d’autres entiers naturels
donc, la somme ne peut être que plus grande que 6.
Le résultat donné ici est plus petit et de surcroît négatif.
Pour ma part, incohérence, peut-être due à un artifice de calcul faux.
III. Suite et Série
Par esprit ludique, j’essaie de me refamiliarisé avec ces dernières, étudiées (dut informatique) il y a un certain temps déjà…
Je n’arrive pas à voir la différence entre ces 2 notions.
Le parcours sur le web n’éclaircit pas les choses, bien au contraire.
Un certain nombre de personnes se pose la même question.
Suite = ensemble d’éléments indexés (ordrés) par N.
Série = ensemble d’éléments indexés (ordrés) par N. On utilise la somme des éléments de la série.
Mais parle t-on aussi pour une suite, de la somme des éléments de la suite?
J’en conclu que c’est pareil, mais alors pourquoi utiliser 2 termes?
Les maths, soit disant rigoureuses, n’ont pas la spécialité d’être très claires sur certains points.
Est-ce la faute à ceux dont le rôle est d’expliquer? Eternel débat…
En tous cas, cela serait sympa à ceux qui savent (!) d’éclaircir mes interrogations.
Merci d’avance.
La série est la somme des termes d’une suite
Je suis d’accord que dès l’exercice d’échauffement, on introduit une mauvaise conception de l’identité des suites infinies. On pose A = 1 – A. Alors qu’il faudrait poser B = 1 – A. En effet, dans le membre de gauche, on ne peut pas remettre A vu qu’à droite ce n’est pas la même suite.
Nous avons au départ une suite infinie du type 1 – 1 + 1 – … à n termes. Mais ensuite nous avons la suite 1 – 1 + 1 – … (n-1) termes. En mathématiques, il est impossible de dire que la première suite est égale à la seconde. Il y a tricherie dès le départ du raisonnement. Vous volez un 1. Le A = 1/2 est farfelu. C’est une moyenne probable, mais la valeur n’est pas calculable car elle oscille infiniment entre 0 et 1 et uniquement ces valeurs, telle une onde carrée.
Pingback: Cabinet curiosite | Pearltrees
Cette équation n’est que de la branlette intellectuelle, pour arriver un tel résultat il faudrait créer une autre science mathématique à mi chemin entre les math et la physique, mais faire passer ça pour un calcul mathématique ça ne colle pas.
comme cité plus haut l’explication de 0*1 = 0*2 donc 1 = 2 illustre tout a fait la problématique.
Dans ce cas on peut dire que 1 + 1 = 3 ou 4 ou 5 ou +
Explication, dans la nature en additionnant un mâle d’une même espèce avec une femelle on obtient un ou plusieurs descendants, 1 + 1 = 3 ou 4 ou 5 ou + ce calcul prête à sourire à juste titre, de la même manière il est valable dans la nature mais ce n’est pas un calcul mathématique.
Allez expliquer aux mathématiciens qui travaillent sur les séries divergentes qu’ils font de la branlette intellectuelle !
Je suis sympa, je vous offre la bible de la branlette intellectuelle sur le sujet : https://archive.org/details/DivergentSeries
(par Hardy, le branleur en chef ! https://en.wikipedia.org/wiki/G._H._Hardy)
Ouah, épatant ! L’argument d’autorité, arme scientifique entre toutes (ou pas). Vous en voulez d’autres des sommités (à la pensée sommaire) intellectuelles qui prennent de la place sur wikipédia ? Il y en a une liste longue comme le bras, et encore, si écrit en caractères microscopiques. Non pas que je nie la totalité de l’apport de Hardy, loin s’en faut, mais sur ce point, permettez un petit ricanement.
#ces-scientifiques-devraient-arrêter-de-jouer-avec-l’infini,-ils-se-ridiculisent-à-chaque-fois.
J’allais fournir la démonstration de la branlette, mais vu que je suis ignoré en général, je l’ai mise en bloc note, pour un futur éventuel livre. Sinon je souscris, de la pure branlette intellectuelle, ces mathématiciens de l’infini, qui n’ont certes pas pour infinie leur cohérence intellectuelle.
Bonjour,
je vois à l’échauffement :
A = 1 – 1 + 1 – 1 + 1 – … = 1 – (1 – 1 + 1 – 1 + 1 – …)
donc :
A = 1 – A
je ne suis pas d’accord car la partie entre parenthèse vaut A-1 et non pas juste A puisque l’on a enlevé 1, même si A tend vers + l’infini, il y aura cette différence qui sera toujours existante. Et cela même si on ajoute ou soustraie une infinité de 1.
Exact.
bonjour,
j’ai une question: que vaut α=1+1⁄(1+1/(1+1/(1+1/(1+⋯.))))
Facile, le nombre d’or ! Voir mon récent billet sur les fractions continues
Hello
Ce qui est marrant c’est quand on part d’un côté de la fraction continue et de l’autre de x²=x+1 et qu’on les fait se rejoindre au milieu (en tutoyant Fibonacci au passage).
[Me suis amusé à ça une nuit d’ennui sur un cahier de brouillon dans mon lit ^^]
Merci !
J’ai recemment découvert ce résultat qui rend joyeux avec Micmaths, sans doute déjà cité, mais je restais sur ma faim..
(https://youtu.be/xqTWRtNDO3U)
Voilà elle est là l’erreur : dès le début, vous partez d’une suite infinie pour en faire un résultat fini. Vous donnez, une valeur pour A égale à 0.5 ou à 1/2 ; certes, valeur probable, mais fictive car indécidable. Ensuite, je ne mets pas en cause le génie de ces grands mathématiciens ni la justesse de leurs calculs, je dis logiquement et irrespectueusement que leurs calculs ne sont que de la branlette cérébrale, du fait même qu’ils mathématisent et développent à partir d’une donnée erronée qui sous-tend par l’abstrait qu’A équivaudrait à 0.5 ou à 1/2.
Avec cette opération : 1+2+3+4+5+6+7+… = -1/12 ! Nous sommes dans la croyance…
Si on prend ces séries, mais en les arrêtant à six nombres, on obtient : A=1-1+1-1+1-1=0, alors A=-1+1-1+1-1+1=0. Ensuite si on ajoute 1 à -A, cela donne : 1-A soit 1-1+1-1+1-1+1=1, sauf cette fois on n’obtient plus du tout l’égalité de départ 1-A=A. Le fait de prendre des suites « infinies » implique une « complétude » dans le sens où on ne peut plus ni ajouter ni retrancher un terme sans que la suite infinie perdre aussitôt sa fonction de suite infinie. Si on ajoute à l’infini un nombre alors, c’est que l’infini en question n’était pas l’infini ; et si on enlève à l’infini un nombre alors, il n’est plus l’infini. Il en ressort que toutes les suites infinies sont des infinis, et que tous les infinis forment le même infini d’où le résultat final qui est : A=B=C, en conclusion, jamais au grand jamais, un infini même choisi comme 1+2+3+4+5+6+7… ne peut être égal à -1/12, car égal à l’infini. A l’inverse, peut-on démontrer que zéro n’est pas égal à zéro ? Le zéro et l’infini sont peut-être les deux plus grandes énigmes de la science et en même temps, des révélateurs ; car le zéro en pouvant se situer sur n’importe quel point de l’espace tend à promouvoir l’existence d’un Univers granulaire ; et l’infini d’un point de vue temporel est bien plus proche de : « Rien ne se perd, rien ne se crée, tout se transforme. » de Lavoisier que de la notion d’éternité exprimée par le temps chronométrique t qui n’a de réalité que sa conversion en distance.
Après le « alors », il faut lire -A, j’ai oublié le moins dans mon texte au-dessus.
(on obtient : A=1-1+1-1+1-1=0, « alors » -A=-1+1-1+1-1+1=0.)
Un « beau » raisonnement niveau 3 élèves !
Mon raisonnement que vous jugez stupide, parce que peu évolué mathématiquement, est pourtant supérieur à cette égalité improbable 1+2+3+4+5+6+7+… = -1/12 qui se fonde sur une acceptation incongrue : le fait que l’on puisse ajouter ou retrancher un chiffre à l’infini sans que cela ne le modifie.
Non je n ai pas dis stupide, ça me dépasse également malgré des études de math assez poussée, mais il faut accepter de ne pas comprendre. Des mathématiciens de renon ont bien potassé le sujet. La mécanique quantique défie aussi notre intelligence.
Dites vous que ce résultat « marche » dans l effet Casimir.
Désolé d avoir été un peu provocateur
Et ça se permet de parler de « branlette cérébrale » sur les calcules présentés dans l’article…
Eh! bien si ! Il y a des choses qui se perdent. Comme le fait que ce n’est pas de Lavoisier mais date d’au moins d’Aristote…
J’appelle branlette cérébrale, tout ce qui est vain et qui ne sert à rien, même si l’intégralité des calculs sont exacts, et vu les réponses laconiques que suscite mon raisonnement, je pense désastreusement qu’il n’y a pas que les étoiles qui s’effondrent sur elle-même.
Et sur quoi te bases-tu pour affirmer que c’est vain et que ça ne sert à rien ?
C’est bien gentil de vouloir faire de la poésie mais ça n’ajoute pas de valeur a ton « raisonnement » pour autant. Que je qualifierais au mieux d’opinion vu le niveau d’élaboration…
Dans ton poste tu parts sur une somme finie a 6 termes, mais tu dois bien te rendre compte que tu peux prendre autant de termes que tu voudras une somme finie n’est pas une somme infinie, les deux n’ont rien à voir.
Tu pourras prouver ce tu voudras avec une somme finie, il n’y a pas de raison que ce soit toujours vrai avec une somme infinie.
Le reste de ton poste est un juste un délire pseudo-métaphysique sans le moindre sens.
Donc prière d’arrêter de prendre de haut des personnes bien plus compétente que soi quand on y connait rien dans un domaine ou sur une question en particulier.
Tu as toi-même démontrer ta faible compréhension du concept d’infini en mathématique, tu n’es donc certainement pas la personne la mieux placer pour vouloir remettre à leur place ceux qui ont produit ces équations sur ce sujet précis, surtout en manquant de respect comme tu l’a fait.
La branlette cérébrale est pourtant une des activités principales du genre humain, elle n’est pas sectaire et touche à toutes les catégories sociales du chef d’entreprise au sans domicile fixe. On l’apprend tous très jeunes avec le coloriage, la satisfaction des enfants qui remplissent des portions est à l’égal de ces mathématiciens qui remplissent des exercices ; ils ont réussi, et là seulement est leur exploit parce qu’ils ont réussi à combler du vide et non pas à apporter de la nouveauté pouvant être concrétisé.
« Et sur quoi te bases-tu pour affirmer que c’est vain et que ça ne sert à rien ? »
Je me fonde sur les hypothèses de Chaman (j’en prends la paternité, le ridicule ne tue pas) : « Si l’on ajoute un nombre à l’infini, alors, c’est que l’infini en question n’était pas l’infini. Si l’on enlève un nombre à l’infini, alors, l’infini n’est plus l’infini. »
Voilà, ces hypothèses impliquent l’impossibilité de cette somme A=A-1, étant donné qu’A est une suite infinie. Et si j’ai pris des suites finies, c’était seulement pour marquer le fait qu’un ajout ou un retrait n’est jamais anodin, sauf l’emploi du zéro qui est en sorte l’antonyme de l’infini, alors que les mathématiciens tiennent à tort – ∞ comme l’inverse de + ∞ : ce genre de détail, c’est aller de l’avant quant à la compréhension de ce qu’est l’Univers, notamment cela indique qu’il existe un seuil subatomique sur lequel repose la matière-énergie, ce qui sonne le glas de l’infiniment petit. De plus le concept mathématique de – ∞ et de + ∞ avec zéro comme centre n’est pas modélisable, car on ne peut pas définir la place du zéro que par l’arbitraire.
Toute théorie est un délire pseudo-métaphysique, non ?
Mon respect pour les scientifiques est mort, le jour où j’ai subi la morgue de l’un d’entre eux, puis la condescendance de certains autres qui est chez eux le prix de leur savoir. Pour le premier, je me suis retenu de le tuer (j’avais mes raisons), mais pour les autres qu’ils n’attendent plus de moi la moindre sympathie, surtout s’ils viennent à moi avec l’esprit écrasant et la pensée ostracisante.
Bien à vous…
Moi au contraire je trouve que ça apporte quelque chose de nouveau et qui donne à réfléchir.
Est une sur de savoir ce qu’est une hypothèse ?
Ton énoncé, qui ressemble plus à un principe, est il sensé être l’hypothèse en question ?
Tu utilises donc un principe hypothétique que tu as inventé toi même pour nier la justesse de l’équation.
Si ça c’est pas se baser uniquement sur sa propre opinion je ne sais pas ce que c’est…
De plus ton hypothèse/principe est complètement faux.
Tous le monde est d’accord pour dire que l’ensemble des entiers naturels est infini { 0, 1, 2, 3, … } il n’a pas de fin.
Et pourtant on lui ajoute bien sans problème un autre ensemble lui aussi infini les entiers négatifs { -1, -2, -3, -4, … } pour former l’ensemble des entiers relatifs qui est infini.
Est ce que du coup ça veut dire que l’ensemble des entiers naturels n’est pas infini ?
Si il l’est bel et bien.
Il y a aussi les nombres réels, entre chacun des entiers relatifs existe une infinité de nombres réels.
Si on décidait de retrancher tous les nombres réels entre le 0 et le 1 (c’est à dire une infinité de nombre) il resterait toujours une infinité de nombres dans l’ensemble des réels.
Mais quoi qu’il en soit, ici il n’est même pas question d’ajouter ou de retrancher à l’infini.
C’est la somme qui est infinie, c’est à dire l’opération, pas la valeur.
La valeur de celle-ci justement on ne la connait pas, beaucoup de gens suppose arbitrairement que sa valeur est infinie.
Donc même ta propre hypothèse erronée ne s’applique pas dans ce cas.
Autre correction au passage: (- infini) n’a jamais été tenu pour l’inverse de (+ infini) mais pour son opposé.
C’est bel est bien 0 qui est considéré comme l’inverse de l’infini.
Et non toute les théories ne sont pas des délires, seulement celles qui ne se base sur rien.
@ Ignotus
« Accepter de ne pas comprendre » : ce n’est pas une attitude scientifique, mais dogmatique que vous me décrivez-là ! C’est bien parce que la mécanique quantique défie notre intelligence qu’elle intéresse et qu’elle sera vaincue (comprise) un jour, du moins sur le plan théorique, car nous n’avons pas les moyens d’expérimenter plus loin que nos propres capacités de recréation. Croyez bien que c’est une chance en physique que cette limitation de recréation, parce que la force et la puissance d’une bombe nucléaire n’est rien en comparaison de celles d’un trou noir.
Je pense que si on trouve pour 1+2+3+4+5+6+7+… = -1/12, alors, c’est qu’il doit exister encore d’autres résultats aussi surprenants que celui-là dans la grande nomenclature des séries infinies. Je suis curieux de savoir s’ils ont tous un équivalent à l’effet Casimir. « Effet Casimir » que je connais mal, car étant peut-être hors de ma portée sur le plan mathématique.
Je passe volontiers sur la provocation, et vous souhaite une bonne nuit.
Merci, j ai bien dit « accepter » à un instant t et non renoncer, ce qui serait dogmatique.
Ce résultat bouleverse nos acquis et doit nous remettre en question sinon la terre serait encore plate.
Bien cordialement
Je suis d’accord avec vous que des connaissances en chassent d’autres (de même que les hommes se suivent), chacune apportant sa nouveauté. Sauf que parfois, les tirs sont dans l’eau, et c’est ce que je pense avec cette égalité :1+2+3+4+5+6+7+… = -1/12, à cause des hypothèses de Chaman qui la contredit.
http://chaman.fr.over-blog.net/2015/10/hypotheses-de-chaman.html
Au plaisir…
Et c’est alors que les mathématiciens et forumeurs nous gratifièrent car en vérité il est dit à celles et ceux qui pratiquaient la numérologie et la pata-science, Houra ! réjouissez vous car après vous avoir reniés ils sont devenu comme vous. Amen
Au début on dirait qu’un « as » à été avalé, il sors d’où, il va où ? Je veux bien qu’en physique il faille être rigoureux, mais si c’est pour auto-justifier un raisonnement courut d’avance, il valait mieux dire : « la fisik est en crise mais je continuerais de rejeter ceux qui ne cadrent pas ».
Un modo pour passer ça en pata-science de l’immobilisme ?
Une fois dans le vide faite moi signe, si vous voyez la lumière blanche, vous ne pouvez pas vous tromper : elle indique inversion de masse à gauche, au-delà en bas, lumière au nord, « t » de la physik : faite du surplace, ça tourne en rond, y’a aussi marqué stargate plus loin et réalité énergétique en travers lorsque beaucoup plus haut y’a écrit réalité spirituelle et encore plus, plus, plus haut, y’a écritures : Destin : « le temps nous gâtent », pi, y’a la créatures d’en haut et celle qui croît d’en bas, alors l’infini s’avance et nous dit : (…)
Sinon j’ai une théorie du tout, elle se finit bien, et elle est bien, je vous la montrerais bien mais je ne sais pas parler dans une salle avec des fauteuils viiiide. Pouvez vous m’help car j’aimerais tant vous apprendre le bon et pas le mauvais. Aller je vous donne un scoop :
Cela commence par essence spirituelle, âme, corps, esprit et cela se termine par essence spirituelle, âme, corps, esprit. Avez vous lu et entendu ?
Une fois j’ai demandé à une femme pour quelles raisons elle portait des talons (pour le coup pas trop voyant). Nous étions à un abris bus et elle devint toute rouge. Je la pris par la main et lui dit, madame dans 20 ans vous allez avoir un problème de dos. Il fallut lire dans ses pensées (c’est de l’énergie) pour comprendre que ses collègues faisaient de même et que la mode lui imposait des obligations vestimentaires.
Alors un autre jour j’ai demandé à mes parents pourquoi que vous avez fait des gosses (oui nous sommes deux) si après c’est tout noir et que y’a plus rien. Il fallut lire dans leur subconscient pour comprendre que c’était aussi la mode ! Il fallait fonder une famille, avoir un travail, une maison, et allez au supermarché et surtout s’occuper de l’administratif et d’aller en vacance car c’était aussi la mode, surtout le ski et la plage, avec du coca et puis surtout pour faire des visites que l’on ne comprend pas.
Logiquement ils voulaient que l’ont connaissent la même fin tragique. (bon débarras)
Puis j’ai compris, alors j’ai élaboré une théorie du tout. Et vous savez quoi. Je meurs d’envie de vous en parler comme si j’étais tout excité mais je me suis rendu compte que : il fallait explorer l’ensemble pour parler de toutes les parties, il fallait apprendre à parler ou garder le silence sur ce que l’on ne SAIS pas, il fallait faire l’étalage de soi-même, il fallait se tourner vers l’intérieur lorsqu’il y a aussi l’extérieur, mais surtout, surtout, il fallait prendre des sandwitchs, de l’eau (et pas que celle de l’abreuvoir) et des couchettes pour que ceux qui entrent à la fin de la conférence puissent vous rendre à la paix.
Autant l’échauffement niveau 1 est convainquant, autant celui de niveau 2 est complètement absurde.
En effet, je pense qu’il est intuitif de dire que A = 1-1+1-1+1-1+1-1+… = 1/2, et en plus on peut le prouver assez simplement, la démonstration étant du niveau lycée avec les suites.
Mais dans l’échauffement 2, il est écrit que B = 1 – B – A. Algébriquement, on voit que B – B s’annule des deux côtés.
Il reste 0 = 1 – A soit 0 = 1/2. Alors là, chapeau, on vient de nous prouver que 0 égale un demi par une transformation douteuse (que par ailleurs je n’ai pas compris tellement elle est étrange, qu’a à voir A là dedans ?). Je tire ma révérence. Non franchement, c’est absurde.
Pourtant, cette manipulation ne relève que de niveau 4ème avec le calcul littéral, et tout élève pourra vous faire cette simplification.
Comme la démonstration repose sur cela, pour il reste complètement faux que si l’on ajoute des nombres toujours + grands jusqu’à l’infini, on obtient un résultat négatif. Absurde. Ou alors très mal expliqué / prouvé.
Jean Martin bonjour,
Si je ne me trompe pas, on obtient une égalité en additionnant ou en soustrayant chaque terme de cette égalité par un même nombre.
Échauffement 2
B=1-B-A
Algébriquement il me semble qu’on voit que B ne s’annule pas des deux côtés mais plutôt que:
2B=1-A
À vous lire
Bonjour
Si je ne me trompe pas , si on admet que A=1/2 c’est a dire que la série de 0 a +oo de (-1)^n converge c’est à dire que la limite de (-1)^n est obligatoirement 0 quand n tend vers +oo … Tandis que (-1)^n n’a pas de limite par usage des suites extraites !
dès le début y’a erreur !!
Bonjour
Beaucoup de bruit (peut-être) pour rien. Comme les différentes sommes sont réécrites pour aider à la solution, je réécris la somme A ainsi : A = (1+1+1+…) – (1+1+1+…). Le résultat est pile poil ZERO. Alors toute la démo tombe à l’eau. Ouf! la somme 1€+2€+… n’est pas égale à -1/12€
Bien cordialement
Je vois un problème dès la première démonstration de A…
Quand on met les parenthèses, on a A=1-1+1-1+1-1+1… + 1-(1+1-1+1-1+1…) Mais la nouvelle parenthèse n’est pas le nombre A, c’est A+1 puisqu’on en a sorti un 1 et qu’après on a changé de signe. Le « … » n’est pas le même. Et là, au lieu de tomber diligemment sur A=1-A et donc A=0.5, on a A=1-(A+1) et donc A=A le serpent se mord la queue.
Si quelqu’un peut me dire comment les grands scientifiques sont parvenus à passer outre cet ecueil, ce serait bien…
Merci d’avence
Ps: Mon scepticisme se trouve renforcé par les formules de Gauss et A dépendrait pour moi simplement de la parité de n…
d’avance* excusez moi
Il y a juste une seul chose :
Si 1 = 1
Et que 2 = 1 + 1
Et que 3 = 1 + 1 + 1
Et que …
Alors 1 + 2 + 3 + 4 + … = 1 + (1 + 1) + (1 + 1 + 1) + …
Donc 1 + 2 + 3 + 4 + … = 1 + 1 + 1 + 1 + 1 + 1 + …
Je pense que c’est parce que l’ on mélange Philosophie Physique et Mathématique.
Je suis assez d accord avec ce calcul simple plein de bon sens mathématique !
opopô^=ô)p
La première démonstration est fausse, donc le résultat ne peut être correct.
En effet le résultat de A= 1 – 1 + 1 – 1 + 1 – … est soit 1 soit 0 ce qui est très différent de 1/2 non !!!
Je voulais d’abord te remercier de la haute qualité de tes articles et de tes vidéos, c’est vraiment au top de la vulgarisation, tout supports informatifs
Sinon il est intéressant de voir les réactions, une véritable déflagration psychologique, qui entraîne déni, rejet, c’est intéressant.
Je pense que les gens se représentent l’infini comme un superlatif de beaucoup.
alors qu’il ne se conçoit pas, nous ne sommes pas « câblé » pour le comprendre,
il ne s’approche que via des artifices mathématiques, transformations, plongements divers …
La non-unicité d’une somme n’est pas nécessairement aberrante, un peu comme la fonction logarithme dans C…
Encore plus marrant, la confusion entre infini dénombrable et l’autre, là, l’innommable (^^), et le flou qui entoure la notion de cardinalité.
Cordialement
Application concret de ce résultat étonnant : vous lancez un engin doté d’un moteur qui permet une accélération d’1m/s.
S est sa distance par rapport au point de départ (au hasard, le sol).
au bout d’une seconde S= 1 mètre
au bout de 2 secondes S=1+2 = 3 mètres du sol
au bout de 3 secondes S=1+2+3 = 6m
etc… la fusée s’élève et accélère…
mais au bout d’un temps infini, vous pourrez trouvez cette fusée enfoncée de 8 cm dans le sol 🙂
Bon ok, le raisonnement ne tiens pas car ma fusée dépasse la vitesse de la lumière au bout d’un moment (ouh le vilain !), et attendre un temps infini avec une pelle pour déterrer la fusée, ça risque d’être un peu long.
BONJOUR
A= 1-(A-1) implique A = 1- A + 1 implique A + A = 2 implique 2 A = 2 implique A = 1
ou
A= 1-(A+1) implique A = 1- A 1 implique A + A = 2 implique 2 A = 0 implique A = 0
justement la limite quand n tend vers + l’infini de la somme des k pour k variant de 1 à n donne la limite de n(n+1)/2 ce qui est +l’inifini et non pas -1/12. De plus si la physique colle à ce résultat ce n’est pas les maths qu’il faut remettre en cause mais la physique actuelle qui est incomplète, ce que chaque physiciens fait et oeuvre sur
Incroyable je viens de lire tout vos posts …déjà superbe article écrit par un homme qui sait remettre en question ses dire si écouter et partager sans juger déjà la bravo …
Pour les commentaires » chamaniques » : l univers comprend trois grandes lois celle de la gravité celle de la complémentarité et celle de la réciprocité (action/reaction) celle qui nous interesse ici est la deuxième si l infini est infini il doit contenir une partie infini disons positive et sa complémentarité une partie infini négative
Donc à un instant t cette infini peut être considéré stable positif plus négatif arbitrairement assimilé au zéro ou en instabilité arbitrairement assimilé à + 1 donc en valeur absolue nous avons affaire à une longueur de onde une oscillation entre 0 et 1 …. le problème est bien sûr le 0 qui selon l univers est la somme de 1 et – 1 n est pas l inverse de l infini qui est la considéré le 0 comme annihilation de l univers…..l inverse de l infini est le fini quand on mélange les deux notions ont met la matière et l animalière ensemble et boummmm effet papillon on change de système et de dimention
Bonjour,
ça fait plusieurs années que j’ai quitté l’université et mes souvenirs de physique sont un peu loin, je m’excuse par avance si j’enfonce des portes ouvertes où si je dis de grosses bêtises.
Pour A = +1 -1 +1 -1 +1
Si on fait la somme des termes à chaque étape, on trouve:
1 0 1 0 1 0 1 …
La suite ne converge pas mais elle ne tend pas non plus vers l’infini.
A remarquer que si on commute tous les +1 à gauche et tous les -1 à droite, il n’est plus évident que ça donne le même résultat: on a + l’infini – l’infini. Intuitivement on a envie de dire que la somme vaut 0 ou est indéfinie mais c’est déjà un résultat différent.
Autre remarque, si je lance la série sur un ordinateur et que je l’arrête après un un moment, je trouve soit 0 soit 1 et la valeur moyenne est 1/2…
Maintenant B = 1 -2 +3 -4 +5
La somme vaut 1 -1 2 -2 3 -3
On voit ici que la somme n’a pas le même comportement.
Si j’arrête la suite après n itérations, je me rends compte que la moyenne des termes générés vaut 0 si n est pair et vaut (n+1)/2n si n est impair.
Si n est grand et grand, alors la moyenne tends 1/2.
Une nouvelle fois, si je lance le calcul de la moyenne des éléments générés par ordinateur et que l’arrête aléatoirement après un temps suffisamment long, je trouverai soit 0 soit 1/2 et en moyenne, en moyenne j’observerai 1/4.
Ça me trouble car il me semble y voir une analogie avec la mécanique quantique. Est-ce que ces valeurs observables par simulation informatique ont une analogie avec les observables en mécanique quantique ?
Encore merci pour votre travail sur ce blog et votre chaîne youtube.
Bonjour,
B = 1 – 2 + 3 – 4 + 5 – 6 + 7 – … = 1/4
soit
B = 1 +(– 2 + 3) + (– 4 + 5) + (– 6 + 7) + … = 1 + 1 + 1 + 1 + …
donc
B = 1 x N avec N = l’infini
On peut en conclure avec certitude que l’infini = 1/4
Ça me rassure 🙂
Il semble y avoir une erreur à l’échauffement, niveau 2 lorsque tu passes de
#1: B = 1 – (2 – 3 + 4 – 5 + 6 – 7 +…)
à
#2: B = 1 – (1 – 2 + 3 – 4 + 5 – 6 + 7 – …) – (1 – 1 + 1 – 1 + 1 – …)
Les 2 # débutent par «1 -». Pour que les 2 # restent identiques il faut que
(2 – 3 + 4 – 5 + 6 – 7 +…) du #1 = (1 – 2 + 3 – 4 + 5 – 6 + 7 – …) – (1 – 1 + 1 – 1 + 1 – …) du #2.
Ce n’est pas le cas car
(1 – 2 + 3 – 4 + 5 – 6 + 7 – …) – ( 1 – 1 + 1 – 1 + 1 – …)
=> (1 – 2 + 3 – 4 + 5 – 6 + 7 – …) + (-1 + 1 – 1 + 1 – 1 + …)
=> ([1 – 1] + [-2 + 1] + [3 – 1] + [-4 + 1] + [5 – 1] + …)
=> (0 -1 + 2 – 3 + 4 – …)
est différent de (2 – 3 + 4 – 5 + 6 – 7 +…)
Qu’en penses-tu ?
Il me semble que le #2 devrait être en remplaçant le «-» par un «+» entre les 2 «()»:
B = 1 – (1 – 2 + 3 – 4 + 5 – 6 + 7 – …) + (1 – 1 + 1 – 1 + 1 – …)
On obtiendrait ceci
=> B = 1 – B + A
=> B = 1 – B + 1/2
=> 2B = 3/2
=> B = 3/4
Merci d’avance.
Hello
Non, les 2 sont bien équivalents :
B = 1 – (1 – 2 + 3 – 4 + 5 – 6 + 7 – …) – (1 – 1 + 1 – 1 + 1 – …)
= 1 – [(1-2+3-4…)+(1-1+1-1+…)]
= 1 – (2-3+4-5…)
Bonjour, je m’appelle Florentin, j’ai lu quelques commentaires et aimerai y laisser le mien…
Je pense que vous cherchez a vous bloquez la cervelle a cause de cet « infini » mais les mathématiques permettent justement d’utiliser et de calculer un « infini » (que ce soit une somme ou autre) a partir du moment ou l’utilisation de cette dernière reste logique d’un point de vue mathématique, et ce site viens de vous le prouver grâce a la démonstration de 1+2+3+4+5+n =1/12 . Je vous accorde tout de même que, malgré la raison mathématique logique, il reste la raison philosophique illogique puisque non trouvée.
La seule chose incompréhensible de l’Univers est qu’il soit compréhensible (Albert Einstein )
Je crois en cette citation même si le problème nous dépasse philosophiquement. N’oubliez pas que nous utilisons meme pas 1/100 des capacités de notre cerveau.
Ceci était mon avis mais je respecte celui de chacun
Bonjour Florentin
Même pas 1/100 ? Comme la théorie des 10% ? Et qui s’occupe de respirer ? de faire battre le cœur ? de faire de nous des homéothermes ? etc. ? Ne serait-ce que ça en laissant de côté la reconnaissance de sons, formes, sensations, mise en relation suivant les aires cérébrales ???
Si on n’utilisait que 1/100, même 10%, de notre cerveau on serait déclaré en état de mort clinique.
J’ai lu la « démonstration » comme quoi la somme des entiers positifs serait un nombre négatif et de surcroît fractionnel (-1/12).
C’est une amusante supercherie, qui s’apparente à un tour de magie, réalisé grâce à une manipulation maline mais tout à fait abusive du langage mathématique.
Cette « démonstration » repose sur un mode d’écriture de l’opération addition qui est fautive, car cette écriture néglige le fait que l’infini n’est pas un nombre avec lequel on peut faire des opérations par exemple : ∞-∞ = ? Ecrire ∞-∞ n’a pas plus de sens que d’écrire 1/0, qui a tout l’air d’être d’un nombre et qui n’en est pas un, c’est une écriture fautive comme il serait fautif d’écrire que ∞=1/0 : l’écriture mathématique convenable est que la limite de 1/x lorsque x tend vers 0 est l’infini
En utilisant la même manipulation fautive je vais démontrer que 0=1 ; ce qui vous l’avouerez est encore plus fort !
Soit S = 1+1+1+1+1+1+1 +…….
Calculons S-S selon la méthode des « colonnes décalées »
S-S = 1+1+1+1+1+1+…
-1-1-1-1-1-1- …
Toutes (*) les colonnes s’annulent, sauf la première et il reste donc 1
Donc S-S = 1
Or par définition même de la soustraction (qui est l’addition de l’inverse) S+(-S) qu’on écrit plus simplement S-S : S-S=0
J’ai donc démontré que S-S = 1 Et S-S=0 donc 0=1.
Je pourrais d’ailleurs démontrer de la même manière que 2 = 0, et donc que 1= 2, et ainsi de suite montrer que tout les nombres entiers sont égaux, ce qui facilite ensuite tout les calculs et rend l’algèbre très simple, quoique bien sûr inutile !
J’ai surtout démontré que ce mode opératoire (colonnes décalées) pour faire des additions quand la liste des nombres à additionner est infinie est fautive
D’ailleurs cette manière fautive de poser l’addition provient du fait qu’on ne peut pas écrire S=∞ et donc -S =-∞, alors pour échapper à cette écriture fautive on en invente une autre tout aussi fautive mais qui a l’air plus innocente !
Pour conclure : si la somme des entiers était un nombre fractionnel négatif voilà qui mettrait par terre la théorie des groupes de Galois, l’addition ne serait plus une loi interne à l’ensemble N et par là les fondements mêmes de l’algèbre s’effondreraient et tous les calculs algébriques deviendraient impossible, ce qu’on comprend bien dés lors que je pourrais démontrer que 0= 1. Si 0=1 , l’algèbre est morte !
(*) Toutes ? c’est là que ce niche la faute … que veut dire ce « toutes » quand il s’agit d’une infinité ? Le propre de l’infini c’est de ne jamais être atteint et donc ne jamais avoir « toutes »
Encore un commentaire sur l’usage des mathématiques en physique : en physique l’infini n’existe pas, car n’existe que je que j’observe de quelque manière que ce soit, et ce que je mesure par le fait même de le mesurer est fini : On ne mesure pas l’infini !
Entre deux nombres réels aussi proches soient-ils il y a encore une infinité de nombres , ça c’est les math ! il y a « continuellement » entre deux nombres une infinité de nombres, en physique entre deux points il fini par y avoir de la « discontinuité », on tombe sur des « grains » des « quanta » … c’est inhérent à l’observation, la physique quantique en découle « nécessairement », mais l’outil mathématique qui permet la modélisation n’est qu’un outil de représentation d’une réalité qui elle est toute autre et nous échappe, :tout ce passe comme si, mais ce n’est qu’une simulation bien comme de, mais une simulation quand même. C’est toujours le même problème que celui de la droite : quand on vous demande de tracer une droite, vous ne tracez au tableau qu’une représentation de la droite car la droite est un objet totalement conceptuel et inexistant et on utilise deux représentation pour manipuler ce concept, soit par la géométrie en traçant une ligne droite soit par l’algèbre en écrivant une équation du type y=ax+b :par abus de langage ont dit » la droite y= ax+b, mais il faudrait dire la droite représenté par l’expression algébrique y=ax+b, car cette expression n’est pas la droite, .. pas plus que la fameuse pipe peinte par René Magritte avec ce titre » ceci n’est pas une pipe » Magritte savait bien g faire la différence entre la représentation d’un objet et l’objet, ce que parfois des scientifiques, même purs et durs, ne savent pas faire, …
Article agréable à lire, bien que je sois chimiste et non matheux 😮
Je me permets juste une petite remarque, pour ceux qui disent que la mathématique n’est que le fruit de l’invention de l’Homme, et que tout est foutaise. Je vous invite tout simplement de nouveau à bien observer la nature et cet Univers infini qui nous englobe. Tout est science, mais dans la majeur partie des cas, cette science, elle nous échappe en réalité. On arrive à la décrypter plus ou moins mais ce qu’il en ressort finalement c’est que cet Univers est régie par une infinité de lois qui sont intransgressible et que tout est crée à la perfection. Il n’y a pas d’hasard et de coïncidence qui tienne.
Pour arriver à expliquer des phénomènes physiques ou autre, on doit bien évidement « inventer » d’une certaine manière en postulant des hypothèses tout en restant cohérent dans notre processus de recherche.
« bien observer la nature et cet Univers infini qui nous englobe »
L’univers n’est pas infini , il ne l’est en apparence que pour nous à notre échelle d’observateur, ce terme n’a même pas de sens en dehors de l’observateur que nous somme, l’infini est une notion mathématique abstraite,il n’y a pas d’infini en physique, ni en chimie , il y a de l’incommensurable pour nous observateur, mais il ne faut confondre nos incapacités inhérentes à notre position d’observateur avec une « réalité « physique infinie.. c’est juste ou trop grand ou trop petit pour nous en tant qu’observateur qui pour observer se trouve coincé par la vitesse limite de la lumière (pour « l’infiniment » grand) et par l’interférence de son observation sur l’objet observé quand il s’agit de de « l’infiniment » » petit (Dans le deux cas l’utilisation du terme « infiniment » grand ou petit est un abus de langage qui veut juste dire trop grand ou trop petit pour nous)
je pense comme l’a dit un grand mathématicien que « deux droites parallèles se coupent à l’infini » , que la suite n’est pas linéaire et qu’à un certain moment elle est nulle ou négative un trou noir en qq sorte apparaît et englouti les chiffres une partie de la série et seuls qq uns y échappent , bon chacun son avis
Bonjour,
en fait j’avais 5 mns à perdre dans ma recherche de quelques notions mathématiques sur les séries…..quand je suis arrivé sur votre blog, bien sympathique….
Bon, niveau lien entre certaines découvertes mathématiques et la physique, je dois me situer bien bas pour certains d’entre vous.
Alors je vous laisse avec mon petit problème, qui vous fera un petit peu réfléchir…, j’espère (et qui peut être fera l’objet d’un nouvel article, mais là….).
-1/4 sera trouver alors une place dans votre monde, comme vous avez « réussi » à trouver une place pour -1/12……
Je reprends votre petite série
A= 1-1+1-1+1-1+1….
mais en fait j’aimerai plutôt l’écrire A=-1+1-1+1-1+1-1+1…. et intervertissant les termes deux à deux, tout « simplement », c’est certain que la démarche n’est pas « normale »…..
En fait à partir de la, on obtient facilement que A=-1/2, et par suite, S=-1/4…..
Voila, je vais repartir à mes recherches,
Bonne continuation.
« En fait à partir de la, on obtient facilement que A=-1/2, et par suite, S=-1/4….. »
En utilisant mal le langage mathématique, donc en écrivant n’importe quoi, on obtient facilement à n’importe quel résultat absurde !
Je peux vous en faire la preuve : En usant de la faute de langage que celle utilisée pour démontrer que la somme des entiers positifs est égale à -1/12, je peux vous démontrer que 0=1, que 1=2, et aussi que si n est un nombre entier, n=n+1 et ce quelque soit n, démonstration par récurrence qui me permet de démontrer que tous les entiers sont égaux entre eux, et qu’il n’existe donc qu’un seul nombre entier .! Où est l’erreur ? Simplement dans la faute de langage … les math c’est d’abord un langage à respecter si on ne veut pas être conduit à dire n’importe quoi
NB dans la »démonstration » la faute de langage vient de la manière de poser l’addition sous forme de « colonnes décalées », cette écriture n’a pas de sens , tout autant que d’écrire par exemple la fraction : 1/0.
Par abus de langage, et un abus qui induit des erreurs de calcul et du coup amène à des résultats faux, certains diront que 1/0= l’infinie, c’est faux, la bonne écriture est d’écrire que 1/r tend vers l’infini quand r tend vers zéro, écrire 1/0 c’est une écriture qui n’a pas de sens.mathématique. Poser l’addition de deux série infinie de nombres par des colonnes décalées est une écriture qui n’a pas plus de sens, et permet alors d’obtenir en effet très facilement n’importe quoi, y compris que je parviens en l’utilisant à démonter, c’est à dire que 0=1=2=2=3 etc .
Ne perdez pas votre temps en de vaine recherche dans une direction qui ne conduit qu’à une fumisterie faite pour épater le badaud.
En toute cordialité
Bonjour,
Alors je réponds à ta remarque…..« En fait à partir de la, on obtient facilement que A=-1/2, et par suite, S=-1/4….. »
En utilisant mal le langage mathématique, donc en écrivant n’importe quoi, on obtient facilement à n’importe quel résultat absurde !
Il aurait fallu que être un peu plus attentif sur les termes qui sont mis entre guillemets dans mes propos….
« réussi », « simplement »; « normale »…..c’est bien pour cela que j’avais 5 mns à …. perdre……
J’espère que l’on converge vers le même raisonnement…..
une question comment fait on pour bouger des parenthèse avec des suite infini ?
sans parler de stabilité ni de linéarité on voit déjà rien quand posant cette question qu il y a un problème non?
Le résonnement donné pour calculer S est complètement faux car la décomposition des sommations infinies n’est pas possible. Rappelons ce résultat concernant la somme des séries convergentes :\\
Si les deux séries $\sum u_n$ et $\sum v_n$ convergent alors $\sum (u_n+v_n)$ converge et on a :
$\sum (u_n+v_n)=\sum u_n + \sum v_n$.\\
Je suppose donc que si l’un des deux séries divergent on ne peut pas affirmer l’égalité de la décomposition.
Par suite le passage de l’identité
$$ S-B = (1 + 2 + 3 + 4 + 5 + 6 + …) – (1 – 2 + 3 – 4 + 5 – 6 + …) $$
à l’identité
$$ S-B = 2 * (2 + 4 + 6 + 8 + …) = 4 * (1 + 2 + 3 + 4 + …)$$
n’est pas valide et n’a pas de sens et ainsi de suite pour le reste du document.
Bien sûr ce que j’ai expliqué ne sera pas compréhensible pour ceux qui non pas étudier les séries, donc je peux réexpliquer à l’aide des notions de limites. Bien sûr la relation $+\infty = +\infty + 1$ est vrai mais je ne peux pas simplifier par $+\infty$ et dire que $0=1$ (similaire à $S=S+1$). De même $+\infty = 2*(+\infty)$ est vrai mais pas possible de déduire $ 2*(+\infty) – (+\infty) = 0 $ et $+\infty=0$.
Les théorèmes ont un grand rôle dans l’évolution des sciences et j’avoue que les commentaires et remarques de chacun ont tout le respect et aident aussi à trouver de nouvelles réponses ou aussi de nouveaux théorèmes .
il y a deux types de délires..délire mathématique et délire en physique..délire mathématique en prouvant n importe quoi par des démonstrations qui paraissent logiques mais au fait non…démontrer par exemple que 1 = 0 ou 5= 15..par des preuves de logique non logique…les délires en physique comme dire que tout l univers n était au début q un point de masse égale à celle de tout l univers….ceux qui délirent comme ceci lorsqu ils sont des individus simples on dit que c est un délire trés trivial…mais lorsqu il s agit d un grand savant qui délire ainsi…on applaudit et on prétend qu il s agit d une grande découverte….alors que c est bien le meme délire.
Je serais tenté de parler de biais de perception…(vade retro creationism) ? Tout l’Univers était donc quoi « au début » ?
Pingback: Aïe ma tête ! – Pierre Carrée
Il est certain que le postulat de base est des plus importants pour effectuer une démonstration quelconque. Un postulat revient à exposer des termes qui ont un sens, dans une phrase qui en exprime, de manière explicite, le contexte, au sein duquel on va déduire ou calculer/démontrer, un résultat, une conclusion admise par la logique et la signification des termes utilisés.
Une somme (addition) est symbolisée par le signe +.
« la somme des entiers naturels est égale à » est déjà en sois un postulat frappé d’une impossibilité logique dans son évocation, pour le contexte mathématique usuel dans lequel on admet: que N est l’ensemble des entiers naturels positifs dont le 0 est exclu, N étant par nature un ensemble indéfini, car composé d’une infinité de nombres.
Que la somme telle qu’elle est présentée sous la forme « 1+2+3+4+5+6+7… et ainsi de suite » relève d’une addition multiple de nombres entiers positifs infinis, dont on ne peut par définition, pas arrêter un unique résultat.
N représente N et non R, Q, Z ou quelque autre ensemble. La somme des entiers naturels positifs donne un résultat positif, que cette somme concerne un résultat fini (par l’addition d’un nombre fini d’entiers), ou tendra vers l’infini au-delà de 0 (par une infinité d’additions et par souci d’écourter la démonstration).
Dans N il n’existe ni fraction ni signe négatif, point.
Je rejoins aaucuntitre, et son commentaire du 30 septembre 2016, car le postulat de base du sujet de cet article ne respecte pas la signification des termes employés dans le contexte mathématique usuel (N, +, =, l’infini). Ces approximations linguistiques combinées à une phrase elle-même frappée d’une erreur logique de conception, permettent alors de démontrer une absurdité, qui amène un résultat tout autant absurde, la belle affaire !.
Dès lors que la démonstration commence par:
» Les mathématiciens ont réussi à prouver que cette immense somme vaut en fait … -1/12 ! Nous allons nous aussi le démontrer, et rassurez vous, dans ce billet on ne va utiliser que l’addition !
Échauffement, niveau 1
A titre d’échauffement, commençons par une somme un peu plus simple :
1 – 1 + 1 – 1 + 1 – 1 + … »
où l’auteur si respectable soit-il, commence, comme il ne l’avait certainement pas écrit plus haut, par une soustraction!!!
nous voilà rassurés, quand à l’intégrité de ses propos, à moins bien entendu, que la soustraction soit une addition et que ceux qui pensent autrement, sont d’aimables farfelus.
Cette modeste analyse, d’un non moins modeste, mais réaliste menuisier, ne vise à dénigrer ou à choquer personne, s’il s’avérait qu’il y ait dans mon raisonnement, une ou des erreurs démontrables par autre chose qu’un lien ou un raisonnement de mauvaise foi, complèxe et/ou hors sujet, je serai reconnaissant à mon contradicteur de bien vouloir les expliciter.
Adishats, merci de votre patiente lecture.
Bonsoir Jean Pierre,
je vous l’assure et peut-être n’ai-je pas été clair dans mon propos (qui à la relecture, manque de précisions et améliorations).
En aucun cas je veux essayer de démontrer que cette somme est égale à -1/12 (ou -1/2 comme vous l’écrivez), c’est tout le contraire.
J’apprécie le commentaire de Rafi Hassen (du 8/01/2017), quant au votre du 8 mars 2016, il démontre par le calcul pur, l’ineptie . Cette prouesse m’étant intellectuellement peu accessible, je ne saurais la mettre en doute, d’autant qu’en conclusion vous arrivez au constat rassurant, qu’il s’agit là d’une erreur mathématique, de par un raisonnement faussé.
Nous arrivons à une similitude de vue par des méthodes différentes, la mienne, qu’un collégien de 5ème peut aisément comprendre, la votre d’un niveau nettement plus compétent en la matière.
J’ose juste espérer que si simplette soit mon analyse, elle démontre tout de même, que la somme des entiers naturels tend vers l’infini à l’exclusion de toute autre solution.
Cordialement.
Salut.
Je ne suis ni physicien ni mathématicien et je n ais pas tout compris a la démonstration.
Pour ce qui est des formules je vous crois sur parole mais la façon d énoncer le sujet est tronqué.
Premièrement: vous ne précisez pas qu’ il faut trouver la moyenne infini de S=1+2+3+4… mais la somme.
deuxièmement: pour commencer avec A=1-1+1… n est pas égal a 1/2 mais tend vers 1/2 au dessus de 1/2 se qui fait une grosse différence et n’élimine pas cette maudite infini.
de même pour B puis pour S.
sa fait longtemps que je ne fais plus des math mais je vous laisse le soin de calculer la limite de s qui n est pas -1/12 mais tend vers -1/12 depuis le haut ou le bas je ne me souviens plus un truc comme sa.
peut s écrire sous la forme P(A)=lim n-inf nA/n
cordialement.
petite correction pour A.
A est de manière alternatif égal a 1/2 puis tend vers 1/2.
de plus A=1-A est faux A=1-A (n-1)
et pour S=-1/12 négatif sa m’intrigue aussi.
je réfléchis.
merci.
J’ai compris, en fait il y a une erreur d interprétation.
Vous pouvez le vérifier en fessant un petit tableau pour A avec n nombre de chiffre âpre l égalité.
Exemple:
An=
A1=1
A2=0
A3=1 etc
Si vous appliquez la formule A=1-A alors vous décalez les parenthèses et par la même occasion les résultats.
Exemple avec An=1-An
A1=0
A2=1
A3=0 etc
Quant vous décalez les parenthèses vous n avez pas An=1-An mais
Exemple An=1-An⁻¹
Pareille pour Bn=1-Bn⁻¹-An⁻¹
Du coups la formule juste pour Sn=(1-Bn⁻¹-An⁻¹)3
Ensuite vous pouvez obtenir la moyenne M de (An) (Bn) et de (Sn) quant n tendent vers l infini.
Exemple pour M(An) tend vers inf.
M(An)=lim n-inf (An+An⁻¹+An⁻²+…)/n
Je remplace An⁻¹ par 1-An « simple a prouver ».
M(An)=lim n-inf (An+(1-An⁻¹)+An+…)/n
J’enlève l infinité d addition.
M(An)=lim n-inf An+1-An/n forme asse simplifier.
Il est possible de l écrire sous d autre formes encore mais je vais vous épargner des tonnes de calculs d autant plus que mon niveau en math est dépassé.
D’ailleurs si des personnes sont susceptible de simplifier la formule merci et de trouver le résultat pour M(An) puis M(Sn).
Cordialement,
Thomas
re salut, excusez moi je ne suis pas fort en math.
j ai fais une erreur mais bon le résultat est surprenant
pour la moyenne de M(A) je me suis trompé donc je recommence et je donne dirrectement le résultat.
M(An)=lim n-inf 1/2An+1/2(1-An)
peut importe la valeur de n la moyenne est au toujours 1/2 je peut donc conclure et écrire que M(A)=1/2
cerise sur le gâteau j ai calculer M(B).
je ne décrirais pas la méthode car je suis feneant.
la méthode est différent.
le résultat est.
M(Bn)=lim n-inf (n⁻¹An)/n
demain je cherche la moyenne de S M(S).
salut quel casse tette.
je m aspersoir que Sn=Bn/3 est fausse aussi
il suffis encore une foi de faire un petit tableau.
S1=1≠B/3=1/3
S2=3≠B/3=-1/3
S3=6≠B/3=2/3
donc avant de calculer la moyenne de S je vais essayer de trouver Sn pour une valeur juste.
re salut.
je viens de trouver la valeur de Sn pour tout n.
je sort la formule en vrak elle peut être simplifiable ou écrite diférament y a pas de problème.
se qui compte c est pas le résultat c est le raisonnement.
Sn=Bn(An-(1-An))((1-An)+n)
la façon de trouver une formule est toute simple encore nos petits tableaux.
n=Cn | An | Bn | Sn | Bn-Bn⁻¹=1-An | (1-An)-An | An-(1-An)
1 1 1 1 0 -1 1
2 0 -1 3 1 1 -1
3 1 2 6 0 -1 1
4 0 -2 10 1 1 -1
5 1 3 15 0
6 0 -3 21 1
7 1 4 28 0
8 0 -4 36 1
9 1 5 45 0
10 0 -5 55 1
cette liste est exhaustive on pourait y rentrer les moyennes aussi voir même les nombres premier.
je mange.
cette apprème je calcule la moyenne de M(Sn).
excusez moi le tableau a supprimé les espaces je le réécris donc mais avec des virgules pour remplacer les espaces.
n=Cn,,,,,,,,,,,,,,,,1,,2,,3,,,4,,,5,,,6,,,7,,,8,,,9,10
An,,,,,,,,,,,,,,,,,,,,1,,0,,1,,,0,,,1,,,0,,,1,,,0,,,1,,,0
Bn,,,,,,,,,,,,,,,,,,,,1,-1,,2,,-2,,3,,-3,,,4,,-4,,,5,,-5
Sn,,,,,,,,,,,,,,,,,,,,1,,3,,6,10,15,21,28,36,45,55
1-An=Bn-Bn-1,,0,,1,,0,,,1,,,0,,,1,,,0,,,1,,,0,,,1
1-2An,,,,,,,,,,,,,,-1,,1,-1,,,1,,-1,,,1,,-1,,,1,,-1,,1
2An-1,,,,,,,,,,,,,1,-1,,1,-1,,,1,,-1,,,1,,-1,,,1,,-1
par la même occasion j ais simplifier Sn=Bn(2An-1)(1-An+n).
oups petite correction.
n=Cn,,,,,,,,,,,,,,,,1,,2,,3,,,4,,,5,,,6,,,7,,,8,,,9,10
An,,,,,,,,,,,,,,,,,,,,1,,0,,1,,,0,,,1,,,0,,,1,,,0,,,1,,,0
Bn,,,,,,,,,,,,,,,,,,,,1,-1,,2,,-2,,3,,-3,,,4,,-4,,,5,,-5
Sn,,,,,,,,,,,,,,,,,,,,1,,3,,6,10,15,21,28,36,45,55
1-An=Bn-Bn⁻¹,,0,,1,,0,,,1,,,0,,,1,,,0,,,1,,,0,,,1
1-2An,,,,,,,,,,,,,,-1,,1,-1,,,1,,-1,,,1,,-1,,,1,,-1,,1
2An-1,,,,,,,,,,,,,,,1,-1,,1,,-1,,,1,,-1,,,1,,-1,,,1,-1
bon jarrette de sacagner vautre cite.
c est un travail fastidieux pour trouver la moyenne de M(s).
il faut au moins une page de calcul.
il y a bien une suite logique.
les nombres premier apparaissent avec une suite logique il me sera donc possible de trouver la moyenne mais je n ais pas finit.
quant j aurais tout mis au propre je le publiais sur ma page facebook thomas guitard.
en travaillant bien il me faudra bien plusieurs jours.
On a un nouveau Ramanujan, ou un Jean Ramanu !!!🤓 â la Guitar 🤡
@Mile Belin +10000
Ouais, c’est bien le genre à Manu ^^
salut sa avance.
j ai fais d un méga brouillon un autre brouillon plus lisible.
en revérifiant je me suis encore tromper sur la moyenne de B.
M(Bn)=lim n-inf (Bn*An)/n
bon c est pas très grave sans la démonstration c est difficile de comprendre.
j ai donc trouvé la somme de A de B et de S et la moyenne de A de B mais pas encore de S.
sa a l aire ardu.
en fait il faut trouver une suite logique au dénominateur de la moyenne qui est en fait S¹+S²+S³+…..
et la sa se gâte j ai déjà écris une page entière jusque a n=30.
je peut déjà voir plusieurs suites logiques mais une page n est pas suffisent pour conclure a une suite logique.
il me faut encore écrire une ou deux pages.
de plus j ai enrichis mon petit tableau des formule il est possible d en écrire a l infini dans la mesure du raisonnable.
amicalement.
Thomas.
Bonjour,
Je crois que la première erreur dans le calcul est que A ne peut pas être égal à 1-A ;
par exemple: A=1-1+1-1+1=1
1-A=1-(1+1+1-1+1)=0 qui n’est pas A c’est évident!
Autre chose concernant la suite C=1+2+3+4+…cette suite peut être écrite comme suit:
C=1+(1+1)+(1+1+1)+(1+1+1+1)+…=1+1+1+1+1+1+1+… qui d’après certains = -1/2
C=-1/2 ou -1/12
Mystère et boule de gomme!
Je me corrige 1+1+1+1+1+….+= inf 🙂 🙂
C=1+2+3+4+…..=1+(1+1)+(1+1+1)+(1+1+1+1)+….+=1+1+1+1+….=inf
La personne qui a écrit S connaissait elle déjà la réponse?
On pose
A= 2 – 2 + 2 – 2 + 2 – …
On peut ensuite observer que
A= 2 – 2 + 2 – 2 + 2 – … = 2 – ( 2 – 2 + 2 – 2 + 2 – …)
Mais on reconnait que le terme entre parenthèses n’est autre que A lui-même, on a donc l’égalité
A = 2 – A
A = 1
De même
A= – 3 + 3 – 3 + 3 – …
A= – 3/2
Et
A= 4 – 4 + 4 – 4 + 4 – …
A= 2
Ou encore
A= 1/2 – 1/2 + 1/2 – 1/2 + 1/2 – …
A= 1/4
La valeur qu’on affecte à cette égalité (s’il y en a une à affecter) est donc fonction du premier terme
On peut donc se poser la question:
Est-ce qu’un « premier terme » a un rôle quelconque quand on considère une somme infini oscillante?
Et si A = … 1 – 1 + 1 – 1 + 1 – 1 …
On a l’infini avant, et l’infini après, comment poser le problème?
La valeur à affecter serait-elle 0?
Si on tombait né à né avec cette somme:
A = 1 – 1 + 1 – 1 + 1 – 1 … au millième terme sans pouvoir observer le premier terme devrait-on remonter jusqu’au premier terme pour connaitre la valeur de cette somme sur l’axe des y?
je vous donne indice
S=1,+2,+3,+4,…….
cette écriture est une liaison entre deux écriture l une finit a gauche l autre infini a droite.
a droite il faut bien séparer les valeurs.
la réponse a la valeur de S je ne la connait pas.
cette écriture donne d autre réponses.
nez à nez
je n ai rien trouver d important sauf qu il faut reformer quelques truques en mathématiques.
un exemple
conventionnellement pour une puissance, par exemple A^2=A*A.
2 correspond au nombre de A
du coups dans la parti droite de mon tableau, la partie infini la première casse est vide. sa pose problème.
il est possible de mettre un sparadrap mais c est laid en math.
intuitivement le chiffre 2 correspond au nombre de multiplication tout comme naturellement on compte a partir de 1.
et je pense que chez les mathématicien sa doit être un débat houleux.
cordialement.
a j oubliais de dire.
je m interdit formellement de toucher a la parti de droite, la parti infini.
sous pêne d avoir un méga bug.
au début je fessait un grand tableau qui liste tous les
B = 1 – 2 + 3 – 4 + 5 – 6 + 7 – …
A= 1 – 1 + 1 – 1 + 1 – …
S = 1 +2 + 3 + 4 + 5 + 6 + …
puis je fais des relations entre S A B, des parti fini a gauche.
plus sa va et plus je descend le tableau et plus le tableau s alourdis et n apporte presque rien.
miraculeusement je remonte se tableau et pas mal de chose se simplifie.
le tableau est un peut comme un big bang mathématique.
j ai abandonner le tableau car je pense que se n est pas sous cette forme qu il faut écrire.
je travaille sur les ((produit,fraction)(puissance,racine)) ((negatif,positif)(paire,impaire)) (valeurs numerique(1,2)(AB))
je pense que se sont des familles mais ne le prenez pas a la lettre.
du coups je me retrouve avec 3 familles et des tableaux incompréhensible et la je bloque.
bon je continu de patauger.
une façon séché de résoudre le problème serait de dire qu une écriture finit ne peut pas être égale a une écriture infini.
∞=∞
S=S
S≠∞
donc
-1/12≠+1+2+3+4……
peut être que
-1/12*∞=1+2+3+4…
ou quelque chausse qui ressemble a sa.
sa y est j ai compris.
prenez
……+1-1+1-1+1-1……..
couvez le en deux au niveau du-1 et vous avez.
-1/2+1-1+1-1…..=-1/2+1-1+1-1……
coupez le au niveau du+1
1/2-1+1-1+1……=1/2-1+1-1+1…….
coupez le entre deux chiffres et vous avez un presque égal un cataclysme pour un mathématicien.
a mince fabien a trouver avant moi.
a non
rectification.
……..+1-1+1-1+1-1………
je coupe en deux
-1+1-1+1-1….=+1-1+1-1+1-1……..
0=+2-2+2-2+2-2…..
0/2=+1-1+-1+1-1……….
erreur de ma part je perd l égalité donc interdit d écrire 0=+1-1+1-1…..
mis a par le fait que -1/2=+1+2+3…est une erreur mathématique.
savoir que l’effet Casimir trouve une valeur -1/12 peut informer le lieu de la mesure.
c est a dire entre deux nombres.
auquel cas il n est peut être pas interdit d écrire une inégalité.
Einstein ou t’amis de référentiel.
Classe 6ème.
Leçon 1.
ne pas confondre absis et ordonné.
signal bonnet d’ane.
Einstein ou t’a mis le référentiel.
Classe 6ème.
Leçon 1.
ne pas confondre absis et ordonné.
signal bonnet d’ane.
conclusion.
si vous enlevez tout se qui est faux.
autrement dis.
si vous enlevez tout se qui ne sert a rien.
vous été dans le vrais.
Arrêtez vos élucubrations, arrêtez de faire et de dire n’importe quoi , relisez le post de David et le post suivant sur les précisions apportées.
Prenez conscience que ce sujet n’est pas accessible à tout le monde, ce n’est pas vraiment de votre fait. Désolé de décevoir les « matheux » en herbe et renoncez !
Pour Mike, +1
……
+2
+3
+4
+5
mdr!
vous ne m’avez pas compris.
l endroit ou l’on pose l égalité a cette suite infini est l endroit ou l on pose le référentiel.
il est possible de poser l égalité sur un nombre et l inégalité entre deux nombres.
…+1-1+1-1…
je pose l égalité sur +1
…+1-1+1/2=+1/2-1+1….
je pose l’inégalité entre -1 et +1.
…..+1-1+1-1≠+1-1+1…..
puis je dessine le référentiel avec l origine a l endroit ou j ai poser l égalité.
sur le ordonnée vous avez les +1-1+1
et sur les abscisse mettez se que vous voulez vous retrouvez se fameux 1/2.
Thomas ça serait sympa d’écrire un peu moins de messages.
Par exemple en écrivant uniquement l’essentiel, et corriger les fautes serait aussi une bonne chose.
« ah mince fabien a trouvé avant moi » est plutôt de l’ordre du « chat »…
J’espère que tu comprends,
cordialement.
Thomas PS:
Tu n’es pas obligé d’obéir à « arrêtez de ».
Ne prends pas par défaut pour vrai ce qu’on peut dire de ce que tu écris, car tout est relatif, il y a du bon et du mauvais à prendre partout car tout le monde est différent.
Et ne renonce que quand tu l’as décidé.
Je te conseille d’aller visiter le site les-mathemathiques.net ils sauront également t’écouter.
Cordialement
x est un Entier naturel
A: F(x)=sin(180*x-90)
B: F(x)=x*sin(180*x-90)
C: F(X)=x
que l on peut appeler.
A(x)=sin(180*x-90)
B(x)=x*sin(180*x-90)
C(x)=x
ou bien travailler avec des Coordonnées polaires.
ne pas introduire 2 dimension dés le départ oblige par la suite a créer des univers parallèles, 10 dimensions et plus etc.
Prenons un signal simple…+1-1+1-1…
Admettons que depuis l origine de coordonné polaire, le signal part dans toutes les directions puis se heurter a un mur rectiligne percer de deux trou.
depuis ces deux trou le signal se répète puis viens se heurter a un mur rectiligne.
pensez vous aux fentes de Young?
nous avons vu a quel point ne pas introduire une deuxième dimension est fatal.
les coordonnées polaire ne fonctionnent que sur deux dimensions.
je quitte donc le forum pour me consacré a introduire une troisième dimension a la coordonnées polaire,
puis savoir si il faut introduire une quatrième dimension pour le temps.
puis comprendre le changement de référentiel avant d aller plus loin.
cordialement.
Mathologer a aussi fait une bonne vidéo sur le sujet (en anglais) : https://www.youtube.com/watch?v=jcKRGpMiVTw
Ecrivons une suite fini.
A=+1-1+1-1+1
A=+1-(+1-1+1-1)
La partie entre parenthese n est pas egale a A.
De quel droit Ramanujan remplace il la suite infini entre parenthese par A?
Nous ne nous le permetons pas pour une suite fini.
Pourquoi serait il permis de le faire pour une suite infini?
Vous n avez pas compris?
Reprenons cette suite fini.
A=+1-1+1-1+1
A=+1-(+1-1+1-1)
A=+1-(A-1)
A=+1
Maintenant ecrivons la suite infini.
A=+1-1+1-1+1-………..
A=+1-(+1-1+1-1-……..)
A=+1-(A-1)
A=+1
Ramanujan n a pas fait tres fort sur se coup la.
A se demande la credibilite de la phisique quantique?
excusez moi je suis alle trop vite.
Reprenons cette suite fini.
A=+1-1+1-1+1
A=+1-(+1-1+1-1)
A=+1-(A-1)
A=+1
Maintenant ecrivons la suite infini.
A=+1-1+1-1+1-………..
A=+1-(+1-1+1-1-……..)
A=+1-(A-1)
A=+1 .lorsque je fais disparaitre la suite infinie
Ramanujan n a pas fait tres fort sur se coup.
A se demande la credibilite de la phisique quantique?
Sans rajouter une variable les valeurs se retrouvent dans un etat superpose quantique,pleonasme.
Confondre deux object phisique ou mathematique donne un resultat differant selon la fasson de calculer.
Rajouter une variable et tout rentre dans l ordre.
Ramanujan a pris la decision d introduire la parenthese comme variable fixe mais ne la pas fait varier.
de plus l egalite est aussi une variable fixe introduite a la suite infinit.
ramanujan a donc introduit deux variables fixe a la suite infinit, la parenthese et l egalite.
maintenant faite varier la parenthese mais pas l egalite puis faite l inverse.
introduire un outil mathematique que j apelle variable fixe n est pas anodin.
= introduire la variable fixe = sur -1 a pour consequence de faire disparaitre -1.
…..+1-1+1-1+1-1…..
…..+1-1+1=+1-1+1…..
introduire la variable fixe A sur la suite de gauche a pour consequance de faire disparaitre la suite infinit a gauche.
A=+1-1+1-1……
introduire deux variables fixe parenthese a pour consequance de faire disparaitre la partie entre perenthese ainssi que les deux parentheses.
A=+1
prenons une suite d entier naturel.
…+1-1+1-1+1-1…..
placons l egalite sur un nombre de signe negatif puis sur un nombre de signe positif.
…….+1-1+1=+1-1+1-1+1…..
…….-1+1-1=-1+1-1+1-1…..
remplasons la partie de gauche par A puis par B.
A=+1-1+1-1+1……
B=-1+1-1+1……
metons les parentheses.
A=+1-(+1-1+1-1…..)
B=-1-(-1+1-1+1-1…..)
le dernier nombre de la suite infinit est successivement negatif puis positif.
la partie entre parenthese est donc successivement egale a +1, 0 pour A puis -1, 0 pour B.
A=+1-(+1)
A’=+1-(0)
B=-1-(-1)
B’=-1-(0)
A=0
A’=+1
la moyenne de A,A’ est egale a 1/2
B=0
B’=-1
La moyenne de B,B’est egale a -1/2
La moyenne de A,A’,B,B’ est egale a 0.
Maintenant untroduisons 0 entre chaque nombre.
……+1,0,-1,0,+1,0,-1,0,+1,0,-1,0………
Je suis l autre moitié de Ramanujan.
Connaisez vous antoine lavoisier?
🚒. 🚑 🚔 🤢🤢🤢 🎸
L’infini ne commence pas par 1 ni même par 0.
L’infini ne commence pas et ne fini pas.
La Série de Grandi ne décrit que la moitié de l’infini.
https://fr.wikipedia.org/wiki/S%C3%A9rie_de_Grandi
si vous récrivez la Série de Grandi en remplaçant n=0 par n=∞
vous avez une série qui ressemble a :
…..+1-1+1-1…..
et la somme est égale a 0
La somme de Grandi est égale a 0 ou 1, 0 ⋁ 1, puisqu’ elle commence par 0 mais pas les deux au même moment.
La série qui décrit l autre moitié de l infini est.
0-1+1-1+1……..
La somme est 0 ⋁ -1.
excusez moi Fabien et Mike Belin.
j ai un debut decompréention de la definition de convergent et divergent.
la série de Grandi est divergente.
la série de Grandi est divergente car « n » est un entier naturel positif.
se qui n’est pas préciser dans https://fr.wikipedia.org/wiki/S%C3%A9rie_de_Grandi
si « n » est un entier naturel la série est convergente et le terme général tendre vers 0.
n=0 n=∞ n∈N
+1-1+1-1…..=∑(-1)^n
+1+0+1+0…=∑(1+(−1)^n)÷2
+1+1+2+2+3+3…=∑?
+1+2+4+6+9+12+16…=∑??
https://fr.wikipedia.org/wiki/Histoire_de_la_fonction_z%C3%AAta_de_Riemann#Le_m.C3.A9moire_de_Riemann
y a une sacré documentation a lire.
les séries de série de ……. de Grandi sont toutes divergente.
Riemann défini la notion de convergence absolue et s’interdit, ou presque, de sommer les séries divergentes.
en fait je bloque un peut sur la définition de convergent et divergent.
les mathématiciens se sont il mis d accord sur cette définition ou bien il y a deux écoles?
ceux qui affirment que la série de Grandi converge en 1/2 et ceux qui affirment qu elle diverge 1,01,0…..
ma réflexion date d avant le xviie siècle.
allons voir le calcul infinitésimal.
https://fr.wikipedia.org/wiki/Calcul_infinit%C3%A9simal
https://fr.wikipedia.org/wiki/Histoire_du_calcul_infinit%C3%A9simal
se qui est sur pour moi A n est pas égal a 1/2.
il y a trop de failles.
un autre exemple qui désapprouve la méthode de pour Ramanujan et par la même occasion la sommation de Cesàro, la sommation d’Abel et sommation de Borel.
C=1+1+1+1….
C= 1+(1+1+1+1….)
C=1+C
0=1
C=+1+1+1+1……
C=+1(+1+1+1….)
C=+1(+C-1)
0=0
A=+1-1+1-1+1……
A=+1-(+1-1+1…..)
A=+1-(-A+1)
A=+1+A-1
0=0
c est décevant mais le calcul est juste.
on ne peut pas reprocher a la théorie des cordes de faire rêver.
au hasard les dimensions magique 4 ou 5 ou -5
n=0 n=∞ n∈N
+1-1+1-1…..=∑(-1)^n
+1+0+1+0…=∑(1+(-1)^n)÷2
+0+1+0+1…=∑(1-(-1)^n)÷2
+1+1+1….=∑(1+(-1)^n)÷2+(1-(-1)^n)÷2
+1+0+3+0+5…=∑((1+(-1)^n)÷2)×n
+0+2+0+4+0+…=∑((1-(-1)^n)÷2)×n
1+2+3+4+5….=∑((1+(-1)^n)÷2)×n+((1-(-1)^n)÷2)×n=∑n
+1+1+2+2+3+3…=∑?
Il y a quand même une sorte d’escroquerie au début :
Car la première série A=1-1+1-1… etc. peut aussi s’écrire A=(1+1+1+1…)-(1+1+1+1…)
Soit A=OO – OO (l’infini moins l’infini) ce qu’il me semble est indéfini …
En fait pour n0 à n=OO, la suite A=(1-1+1-1…) en regroupant les « 1 » peut aussi s’écrire :
A=(1+2+3+4+5…)-(1+2+3+4+5…)
A=∑1^n – ∑1^n
ou encore :
1=(1+2+4+8…)-(1+2+4+8…)
A=∑2^n – ∑2^n
Etc …
Soit pour x, y entiers >=0
A=∑x^n – ∑y^n
Et même :
A=(1+2+3+4+5…)-(1+2+3+4+5…) + (1+2+4+8…)-(1+2+4+8…) etc…
A=∑∑x^n – ∑∑y^n
A=∑∑∑x^n – ∑∑∑y^n
Etc …
Étonnant non ?
Je sens que je vais en énerver quelques uns en revenant sur la démonstration de la première suite A=(1-1+1-1…) donnant A=1/2, même si le raisonnement semble exact je pense qu’il y anguille sous roche et je reste persuadé que le résultat est faux, trois tentatives pour essayer de le démontrer :
1- La suite A étant répétitive et infinie, rien n’empêche de la faire commencer par -1, sans supprimer le premier +1 le plus à gauche mais en le rejetant à la fin de la suite :
A=(1-1+1-1+1…)=(-1+1-1+1… +1), jusque là on a rien changé quant à la valeur absolue de la suite, puis on procède au mêmes manipulations et calculs que précédemment :
A=-1+(+1-1+1-1….+1), attention dans ce cas le reste entre parenthèses est égal à –A,
on a donc A=-1-A et A=-1/2 (au lieu de +1/2 !)
Autrement dit, en partant de la même suite et des mêmes quantités de +1 et de -1, on arrive à deux résultats opposés …
2- Le fait de « sortir » le premier +1 de la suite entre parenthèses est un tour de passe-passe, il n’est pas anodin, il consiste en fait à soustraire 1 à A, tel le reste X=A-1.
Autrement dit X est plus petit que A de 1, ou encore X<A et en aucun cas on peut prétendre former une égalité entre X et A telle qu’elle que c’est suggéré dans A=1-A qui devrait plutôt s’écrire A=1+X.
De plus, même si A et X tendent tous deux vers l’infini, A y tend plus rapidement que X puisque X est plus petit que A, il n’y donc pas d’égalité.
3- En fait, par analogie, la suite A=(1-1+1-1+1…) me fait penser à un phénomène périodique comme un signal carré d’amplitude A prenant alternativement les valeurs de +1V et -1V,
La somme : Σ-1^n pour n=0 à n=∞ peut aussi s’écrire Σ cos (n.π) pour n=0 à n=∞ ce qui se rapproche de mon hypothèse, une alternance de +1 à -1 étant effectuée pour n=2, soit un tour ou 2.π.
En faisant tendre n vers l’infini, cos (n.π) est indéfini et la somme A=Σ cos (n.π) l'est aussi.
Par contre la valeur moyenne d’un signal périodique carré, symétrique par rapport à 0V (sans tension d’offset), est nulle, ce qui me fait dire qu’un phénomène physique démontre clairement que le résultat de A=(1+1-1+1-1 …) ne peut pas être égal 1/2 mais bien 0, si la fréquence est assez élevée c’est d'ailleurs ce que mesurera un voltmètre.
Salut Antoine, je trouve aussi que c’est déstabilisant.
Je sais aussi qu’il faut faire attention à la façon dont on utilise les outils mathématiques, beaucoup ici ont fait des remarques qui ressemblent aux tiennes et je t’invite à lire tous les commentaires, par exemple David précise que:
» la « mise bout à bout » des deux sommes est interdite, ça n’est pas une opération linéaire »
Cordialement
n=0 n=∞ n∈N
+1-1+1-1……………..=∑(-1)^n
-1+1-1+1-1……………=∑-(-1)^n
+1+0+1+0……………=∑(1+(-1)^n)÷2
-1-0-1-0……………=∑-(1+(-1)^n)÷2
+0+1+0+1……………=∑(1-(-1)^n)÷2
-0-1-0-1……………∑-(1-(-1)^n)÷2
+1+1+1……………….=∑(1+(-1)^n)÷2+(1-(-1)^n)÷2=∑+1
-1-1-1-1……………….=∑(-(1+(-1)^n)÷2+(1-(-1)^n)÷2)=∑-1
+1+0+3+0+5………=∑((1+(-1)^n)÷2)×n
-1-0-3-0-5………=∑-(((1+(-1)^n)÷2)×n)
+0+2+0+4+0+….…=∑((1-(-1)^n)÷2)×n
-0-2-0-4-0-….…=∑-(((1-(-1)^n)÷2)×n)
+0+1+2+3+4+5………..=∑((1+(-1)^n)÷2)×n+((1-(-1)^n)÷2)×n=∑n
-0-1-2-3-4……………=∑-(((1+(-1)^n)÷2)×n+((1-(-1)^n)÷2)×n)=∑-n
-0+1-2+3-4+5…………=∑((-1)^n)×n
+0-1+2-3+4-5…………=∑-((-1)^n)×n
+0+0+1+1+3+3+5+5…..=∑n-(1-(-1)^n)÷2
-0-0-1-1-3-3-5-5……….=∑-(n-(1-(-1)^n)÷2)
-0+1-1+2-2+3-3…..…=∑?
+0-1+1-2+2-3+3……..=∑?
+0+1+1+2+2+3+3……=∑?
-0-1-1-2-2-3-3……….=∑?
méthode de Cesàro appliqué a la suite B, pour calculer la moyenne des sommes partielles de B
suite B 1,-2,3,-4,5,-6,……
n=0 n=∞ n∈N
série de B 1-2+3-4+5-6+…..=∑((-1)^n)×(n+1)
suite de la série de B 1,-1,+2,-2,+3,-3,….
série de la série de B 1-1+2-2+3-3+……=∑((3+2×n+(-1)^n)×(-1)^n)÷4
suite de la série de la série de B 1,0,2,0,3,0,4,….
série de la série de la série de B 1+0+2+0+3+0+……=∑(((3+2×n+(-1)^n)×(-1)^n)÷4)×(1+(-1)^n)÷2
moyenne de la série de la série de la série de B
1/1+0/2+2/2+0/3+3/4+0/5+4/6….=∑((((3+2×n+(-1)^n)×(-1)^n)÷4)×(1+(-1)^n)÷2)÷(n+1)
suite de la moyenne de la série de la série de la série de B
1,1,2,2,11/4,11/4,41/12,41/12,97/24,97/24,557/120,557/120,209/40,209/40,1623/280,…..
limite de la série de la moyenne de la série de la série de la série de B quant n tend vers l’infini ?
1+1+2+2+11/4+11/4+41/12+…=lim n→∞∑?=
méthode de Cesàro appliqué a la suite B, pour calculer la moyenne des sommes partielles de B
suite B 1,-2,3,-4,5,-6,……
n=0 n=∞ n∈N
série de B 1-2+3-4+5-6+…..=∑((-1)^n)×(n+1)
suite de la série de B 1,-1,+2,-2,+3,-3,….
série de la série de B 1-1+2-2+3-3+……=∑((3+2×n+(-1)^n)×(-1)^n)÷4
suite de la série de la série de B 1,0,2,0,3,0,4,….
série de la série de la série de B 1+0+2+0+3+0+……=∑(((3+2×n+(-1)^n)×(-1)^n)÷4)×(1+(-1)^n)÷2
moyenne de la série de la série de la série de B
1+0+2/3+0+3/5+0+4/7+0+5/9….=∑((((3+2×n+(-1)^n)×(-1)^n)÷4)×(1+(-1)^n)÷2)÷(n+1)
lim n→∞∑((((3+2×n+(-1)^n)×(-1)^n)÷4)×(1+(-1)^n)÷2)÷(n+1)=tend vers 0
S=-B/3
S=tend vers 0
1+(D-2)÷2×S=0
1+(D÷2-1)×S=0
(D÷2-1)×S=-1
D÷2-1=-S
D÷2=-S-1
D=(-S-1)÷2
encore plus direct on remplace S par la moyenne de S qui est convergent en 1
moyenne de S=∑n÷n=convergent en 1
D=-1
encore plus direct et sans tricher.
1+(D-2)÷2×S=0
1+(D÷2-1)×S=0
(D÷2-1)×S=-1
D÷2-1=-S
D÷2=-S-1
D=(-S-1)÷2
D=∑(-(n+1)-1)/2==-1-3/2-2-5/2-3-7/2-4…….
il ne nous reste plus qu’a tricher et trouver une forme convergente.
D=∑(-(n+1)-1)/2==-1-3/2-2-5/2-3-7/2-4…….
avec la théorie des ensembles il doit être possible de prouver que D ensemble infini ne peut pas être réduit sous une forme fini.
c est déjà satisfaisant que 10 11 et 26 dimensions font partie de D.
Des dimensions négatives, des rationnels de dimensions?!??
cette formule a elle été vérifier? 1+(D-2)÷2×S=0
d’ou sort cette formule?
oups petite erreur sa ne change pas grand chausse.
1+(D-2)÷2×S=0
1+(D÷2-1)×S=0
(D÷2-1)×S=-1
D÷2-1=-S
D÷2=-S+1
D=(-S+1)÷2
D=0,-1/2,-1,-3/2,-2,-5/2,-3,-7/2,….=(-n+1)/2
n, est il un entiers naturels, entiers relatifs, nombres décimaux, etc…?
avec la théorie des ensembles il doit être possible de prouver que D ensemble infini ne peut pas être fini.
c est déjà satisfaisant que 10 11 et 26 dimensions appartiennent a D.
Des dimensions négatives, des rationnels de dimensions?!??
cette formule a elle été vérifier? 1+(D-2)÷2×S=0
d’ou sort cette formule?
-1/12 est ce qui la sépare deux infini
j aurais du commencer a lire par la fin.
merci.
j ai un sacré chemin pour être au niveau.
merci encore.
https://fr.wikipedia.org/wiki/Levier_(m%C3%A9canique)
S=-1/12
-1/12 nous indique ou placer un point d appuis pour qu un poids de 12 kg soit équilibré avec un poids de 1 kg.
découpez le bras de levier en 12 partie puis placez le point d appuis sur l emplacement 12-1=11
notre balancier est équilibrer.
nous retrouvons 11 qui correspond au nombre de dimension pour avoir un équilibre.
quel sens cela peut il avoir?aucune idée.
merci Archimède.
un poids de 1Kg+2Kg+3Kg+……. positionné a 1 mètre d un point d appui équilibre 1 Kg positionné a 1metre ,2m,3m,……
∆ : point d appui
1 ∆ 1 1 1 1…
2
3
4
.
.
.
prenez la suite 1,2 imaginez que ces nombres soit des masses.
placez un point d appuis au deux tiers ou -1/3 c est la même chausse.
la suite est en équilibre.
pareille pour la suite 1,2,3
sa fonctionne donc a l infini.
prenez la suite 1,2,3,…. infini coupez la en trois placez le point d appuis au 2/3, la suite infini est en equilibre.
Archimède avais raison! Donnez-moi un point d’appui : je soulèverai le Monde
non!? bon ok j’arrête.
Oui ! bonne décision 🙇
Une petite recherche sur le ouèbe nous apprend que la première série A=(1-1+1-1+1 …) servant au début de la démonstration est la série dite Grandi …
La solution A=1/2 présentée par l’auteur de ce blog est celle dite d’Euler qui ne la démontre pas et qui fait des entorses sur les opérations sur l’infini, le résultat est donc faux.
On trouve aussi une autre solution plus sophistiquée qui converge vers 1/2, c’est celle de Cesaro et qui consiste à bâtir une suite des résultats partiels de la série initiale puis d’en faire la moyenne : M= 1/n ∑(1, 1/2, 2/3, 4/4, 4/5 …) pour n=1 à n=n et prétendre que M=A, bien que cette solution soit applicable dans certains cas pour des séries convergentes, cette solution est fausse dans ce cas car la série A ne converge pas et la moyenne de la suite n’est pas égale à la somme totale de la série.
Prenez l’exemple du papa radin qui met 1 €uro dans la tirelire de son lardon tous les jours, mais qui lui reprend tous les soirs quand le mioche dort.
Au bout de 20 jours quand le marmot crédule croit pouvoir s’acheter une tonne de bombecs il est très déçu :
le contenu de sa tirelire n’est pas de 10 €uros, ni même de 0,5 €uros [(10 €uros) / (20 jours) = 0,5 €uros] mais bien de 0 €uros et les maths, Euler et Cesaro n’y peuvent rien …
Deux dernières pour la route, deux autres démonstrations qui démontre que la série de Grandi est « incomplète » et qu’elle ne peut pas être égale à 1/2 et qui feront se retourner dans leurs tombes Grandi, Euler et Cesaro :
1 : La suite de Grandi A= 1-1+1-1+1… commence de façon arbitraire pas « +1 » car elle est « incomplète », je m’explique, si on se place n’importe ou sur cette série, on ne peut pas présumer de la valeur du premier terme, +1 ou -1 ?, le choix de départ arbitraire conditionne le résultat : 1/2 ou -1/2, cette solution n’est donc pas universelle …
Cette série est infinie « à droite » et devrait l’être aussi « à gauche », imaginons que nous la coupions en deux et que la partie infinie de droite commence par +1, elle est alors égale à A d’après les entorses d’Euler, la partie de gauche par rapport au point de coupe infinie elle aussi commence par -1 et est égale à –A d’après ces mêmes entorses.
Nous nous trouvons devant le paradoxe de A=A-A …
Que diable ! passons outre et remplaçons les A par la solution d’Euler ou de Cesaro :
soit A=A-A=1/2 – 1/2 ou encore A=0 …
2 : Une autre solution « graphique » et par le calcul nous permettant de voir ce qui se passe en encadrant A :
Dans la série A=1-1+1-1+1… on peut identifier la répétition de « n fois » deux séquences récurrentes équivalentes :
(+1-1) ou (-1+1) toutes deux égales à 0 ; la série A peut donc s’écrire A= n.(1-1) ; tentons de voir ce qui se passe aux limites : la limite de A quand n tend vers l’infini est indéfinie puisque (1-1)=0
et ∞ . 0 n’est pas défini.
Par contre on peut très bien encadrer A par deux équations facilement calculables ; choisissons un n>>>1 non infini mais « très grand » et posons Y+=n(1-(1-ɛ)) et Y-=n(1-(1+ɛ); ɛ étant « très petit » proche de zéro, ça revient à dire que Y+=n(ɛ) et Y-=n(-ɛ) sont de la forme y=a.x (avec x=n et a=ɛ ou -ɛ) soit l’équation d’une droite de pente ɛ ou -ɛ, on voit que ces équations divergent vers +∞ pour ɛ>0 et vers -∞ pour ɛ<0.
Si on choisit un n assez grand et un ɛ assez petit, nos équations Y+ et Y- divergeront lentement tout en restant proche de 0 et en encadrant la série A.
Si de plus pour un n donné on fait la moyenne M de Y+ et Y- on obtient M=((Y+)+(Y-))/2 =0 ce qui démontre une fois de plus que A ne peut pas être égal à 1/2 …
@ Antoine:
Et si la suite était
A= 1-1+1-1+1…
avec pour premier terme 1
Est-ce qu’ils se retourneraient dans leur tombe?
pourquoi se limiter aux entier naturel utilisons les nombres réels.
(-1)^n
et les imaginaires apparaissent.
de façon imager prenez une bouteille écrivez +1 d un coté -1 de l autre.
tournez la.
les imaginaire ne serai se pas le moyen de boire euuuu voire la bouteille dans son ensemble.
PS: quel est vautre impression Mike?
En posant A = n.(1-1) et en remplaçant 1 par i/i et -1 par i^2 on tourne en rond comme avec A= cos (n.π) :
A= n.(i/i + i^2) = n(i.( -i)+ i^2) = n.(-i^2 + i¨2) = n.(-(-1) + (-1)) = n.(1-1) =0 …
De même en posant A= n.(1-i) on arrive à une solution infinie IAI =n.(1^2+1^2)^1/2 …
Bref le A =1/2 il n’y a qu’en fumant la moquette qu’on peut l’imaginer …
(-1)^n=(i×i)^n=(1×−1)^n=(i^2)^n=(1×−i^2)^n
oups
(-1)^n=(i×i)^n=(1×−1)^n=(i^2)^n=(1×i^2)^n=(-i^2×i^2)^n
|-1>+|1>
https://www.youtube.com/watch?v=dNpdMYB8pZs
si sa peut t’inspirer Antoine.
même si je suis très loin de tout comprendre c’est une bonne source d inspiration.
Allez, on se fait plaisir à démontrer une fois de plus que les solutions d’Euler et de Césaro de la série de Grandi sont bidons :
La série de Grandi A= 1-1+1-1+1 … est composée de la somme de deux séries A= X+Y avec X= 1+1+1+1+1 … et Y= -1-1-1-1-1 …
Si on suppose vrai la solution A= 1/2
Cela revient à dire que X+Y= 1/2
Et donc que la différence X – (-Y) = 1/2 qui est nombre rationnel inférieur à 1
Or les séries X et Y sont composées exclusivement de 1 qui sont des nombre entiers, il est donc impossible qu’en les additionnant ou en les soustrayant on obtienne un nombre rationnel plus petit que 1
…
Bonjour,
Excusez-moi, je ne viens rien apporter de constructif au problème et vous prie sincèrement de m’en excuser, mais en lisant les réponses de David aux commentateurs irrespectueux(avec mon niveau en math, je n’ai par ailleurs pas compris grands choses de plus que leur commentaires et en parcourant le reste du billet j’ai hésité entre irrespectueux et ingrats…), je n’ai pas réussi à me retenir de venir ici pour lui dire que je le trouve monstrueux de patience et d’humour…
Je vous prie encore une fois de m’excuser pour mon commentaire, et vous souhaite à tous une très bonne continuation.
Aurais-je marché sur la quatrième dimension du pied gauche sans m’en rendre compte ?
Voulant démontrer que la suite de Grandi (encore elle !) ne pouvait pas être égale à 1/2 j’ai, il me semble démontré le contraire, je m’explique :
Partant de l’idée que la suite A= +1-1+1-1+1-1… était constituée de 2 autres suites imbriquées que je j’appellerai A+ et A- et telles que A= (A+) + (A-) avec
A+= +1_+1_+1_+1 …
A-= _ -1_ -1_ -1_ -1 …
(Notez que les espaces ont leur importance)
Les termes de la suite A, n0, n1, n2, n3 … prennent respectivement la valeur +1, -1, +1, -1 …
La suite A+ n’existe que pour n>= 0 et tous les termes n pairs
La suite A- n’existe que pour n>=1 et tous les termes n impairs
En reportant les points des sommes partielles (n, f(n)) des suites A+ et A- sur un repère orthonormé d’abscisse n et d’ordonnée f(n) on constate que
Tous les points sommes partielles de la suite A+ sont alignés et contenus dans une droite d’équation
y(n)= 1/2.n+1
Tous les points sommes partielles de la suite A- sont alignés et contenus dans une droite d’équation
z(n)= -1/2.n-1/2
A partir de là on intègre ces deux fonctions
∫ y(n) dn= 1/4.n^2+n
∫ z(n) dn= -1/4.n^2-n/2
Et en sommant les deux intégrales
Σ ∫ y(n) + ∫ z(n) = 1/4n^2+n + (-1/4n^2-n/2) = 1/4n^2+n -1/4n^2-x/2= x/2
x/2 est l’aire différence entre les deux courbes
en divisant par x on obtient la moyenne des différences x/2x= 1/2 (constante indépendante de n)
On peut aussi obtenir ce résultat directement sans intégrer en sommant y(n)+z(n)
Σ y(n)+z(n) =1/2.n+1 -1/2.n-1/2 = 1/2
Cette solution me laisse dubitatif …
bravo.
Erratum dans mon précédent post :
Remplacer les « x » dans
« Σ ∫ y(n) + ∫ z(n) = 1/4n^2+n + (-1/4n^2-n/2) = 1/4n^2+n -1/4n^2-x/2= x/2
x/2 est l’aire différence entre les deux courbes »
Par des « n »
« Σ ∫ y(n) + ∫ z(n) = 1/4n^2+n + (-1/4n^2-n/2) = 1/4n^2+n -1/4n^2-n/2= n/2
n/2 est l’aire différence entre les deux courbes »
La variable est « n » et non pas « x » …
la question est. est il possible d appliquer la même méthode pour S?
excusez moi ne je comprend que vaguement le sens d une intégrale.
il va me faut revisser.
Une intégrale est une sorte de somme qui permet de calculer des surfaces proportionnelles à une fonction et à une variable, par exemple : S= V*T la distance S est proportionnelle à la vitesse V et au temps T
Si on dessine un graphique avec T en abscisse (axe horizontal) et V en ordonnée (axe vertical) et qu’on reporte V point par point pour chaque instant T, alors la surface comprise entre la courbe dessinée de V et l’axe des abscisses et entre les instants T0 et T1 est la distance parcourue entre T0 et T1
Si V est une droite (vitesse fixe ou uniformément accélérée), on peut calculer la distance S simplement avec des surfaces de rectangles ou de triangles, sinon il faut faire une intégrale de V(t) entre T0 et T1 : S= ∫ V dt
L’opération inverse s’appelle la dérivée, si on dérive la fonction de la distance S par rapport à T, on obtient l’équation de la vitesse V …
Pour ce qui est de la série S= 1+2+3+4 … = -1/12, je pense pas que ma méthode soit applicable …
En fait j’ai appliqué ma méthode à la série B= 1-2+3-4+5-6+7 … =1/4 et si je ne me suis pas trompé, ça marche !
C’est un plus compliqué, je mettrai la démonstration plus tard …
merci pour l explication j avais déjà fais de la cinématique en mécanique.
sa renforce ma compréhension.
pour calculer directement D nombre de dimension je pense que ce n est pas possible aussi.
D=0,-1/2,-1,-3/2,-2,-5/2,-3,-7/2,….=(-n+1)/2
attention tout de même quant vous trouvez 1/2 pour A et 1/4 pour B vous faite la moyenne.
A n est il pas égal a n/2 ?
Non, les calculs de A=1/2 et celui de B=1/4 sont totalement indépendants.
Je ne calcule aucune moyenne, seulement des « surfaces », voir le (*) NOTA en bas.
Pour comprendre mon raisonnement il faut faire un petit graphique avec deux courbes (la courbe « des plu »s et la courbe « des moins »), mais ici je sais pas comment faire pour en coller un.
Le principe est simple, après avoir tracé le graphique et identifié les lois ou fonctions qui lient la somme partielle de chaque terme positif ou négatif :
– On calcule la surface des termes positifs représentés par la courbe « des plus » du haut (intégrale ou calcul de surface par des formules de géométrie)
– On calcule la surface des termes négatifs représentés par la courbe « des moins » du bas (idem)
– On fait la somme ou la différence entre ces deux surfaces et on trouve un résultat (la différence des surfaces) de type kn ou kx selon la variable choisie (n ou x), k est un coefficient constant (un nombre)
– On divise le résultat obtenu par la variable choisie (n ou x) et on obtient k la constante, 1/2 ou 1/4 qui comme elle est indépendante de la variable (n ou x) semble être le résultat qu’on cherche (*) NOTA …
(*) NOTA : ce calcul est le calcul de la moyenne du reste de la surface restante après avoir fait la somme des aires, et pas de la moyenne de la série, en gros c’est le calcul de la hauteur du rectangle restant (surface divisée par longueur = hauteur) …
La méthode par les moyennes de Césaro, c’est autre chose.
Une autre solution originale à la suite B= 1-2+3-4+5 … =1/4
J’ai appliqué ma méthode à la suite B= 1-2+3-4+5-6+7 … =1/4 pour voir si ça avait de chances de fonctionner, et je crois que oui :
La suite B= 1-2+3-4+5-6+7 … est composée de 2 autres suites imbriquées qu’on peut appeler B+ et B- telles que B= (B+) + (B-) avec
B+= +1_+3_+5_ …
B-= _ -2_ -4_ -6 …
(Notez que là aussi les espaces ont leur importance)
Les termes de la suite S, n0, n1, n2, n3 … prennent respectivement la valeur +1, -2, +3, -4 …
La suite B+ n’existe que pour n>= 0 et tous les termes n pairs
La suite B- n’existe que pour n>=1 et tous les termes n impairs
En reportant les points des sommes partielles (n, f(n)) des suites B+ et B- sur un repère orthonormé d’abscisse n et d’ordonnée f(n) on constate que
Tous les points somme de la suite B+ sont contenus dans une courbe de type y(x)= x^2
Tous les points somme de la suite B- sont contenus dans une courbe de type z(x)= -x^2+k
Ici, j’ai du mal à l’expliquer et j’ai pas mal tâtonné, mais, il faut procéder à un changement de variable, la variable « n » de notre série S ne fonctionne pas directement, par contre la variable « x » telle que x= 1/4n+1 fonctionne parfaitement, pour tout « n » donné >=0 correspond un « x ».
Cette nouvelle variable « x » nous permet de calculer k, qui vaut ici 1/4
A partir de là on intègre ces deux fonctions
∫ y(x) dx= 1/3.x^3
∫ z(x) dx= -1/3.x^3+x/4
Et en sommant les deux intégrales
Σ ∫ y(x) + ∫ z(x) = 1/3x^3 -1/3.x^3+x/4 =x/4
x/4 est l’aire obtenue en faisant la différence entre les deux courbes
puis en divisant par x on obtient la moyenne des différences (x/4).(1/x)= 1/4 (1/4 est une constante indépendante de x (et de n))
On peut aussi obtenir ce résultat directement sans intégrer en sommant y(x)+z(x)
Σ y(x)+z(x) = x^2 – x^2+1/4 = 1/4
Est-ce généralisable à toutes les séries alternées répondant à une loi régulière de type u= +a -b +c -d ?
Solution de la série de Ramanujan S= 1+2+3+4+5 … = -1/12
Ici je ne pense pas qu’on puisse décomposer la série S en deux sous-séries car tous les termes de la série sont de même signe.
Pour connaitre le résultat de la série de Ramanujan S= 1+2+3+4+5 … = -1/12, il n’est pas nécessaire de connaitre le résultat de la somme de Grandi, par contre on peut passer par une opération intermédiaire utilisant la somme des entiers alternés
B= 1-2+3-4+5 … = 1/4 et retomber en partie sur le calcul présenté par l’auteur du blog :
S= 1+2+3+4+5 … = ?
B= 1-2+3-4+5 … = 1/4
-B= -1+2-3+4-5 … = -1/4
S-B= 0+4+0+8+0 … = 4.S
-B= 4.S –S= (4-1).S
-B = 3.S
S= -B/3 = (-1/4).(1/3) = -1/12
CQFD (sous réserve des erreurs de raisonnement et de celles de calcul) …
Erratum, série « B » et variable x= 1/2n+1 :
… il faut procéder à un changement de variable, la variable « n » de notre série « B » ne fonctionne pas directement, par contre la variable « x » telle que x= 1/2n+1 fonctionne parfaitement, pour tout « n » donné >=0 correspond un « x ».
je tente de suivre le vautre raisonnement pour A.
pour continuer de vous suivre.
Pour réviser les intégrales :
https://www.youtube.com/watch?v=jkxNKkmEXZA
encore bravo
merci pour le lien.
en fin des explication simple et compréhensive.
https://www.youtube.com/watch?v=6DHXw5TRzN4&index=5&list=PLVUDmbpupCaotX5idBCunutFUfZvIQFSs
S = 1 +2 + 3 + 4 + 5 + 6 + …
S – B = (1 +2 + 3 + 4 + 5 + 6 + …) – (1 – 2 + 3 – 4 + 5 – 6 + …)
S – B =0+4+0+6+0+8+0+10+0+12……
S – B =4 *(0+1+0+2+0+3+0+4+……)≠4 * (1 + 2 + 3 + 4 + …)
S = 1 +2 + 3 + 4 + 5 + 6 + …
S – B = (1 +2 + 3 + 4 + 5 + 6 + …) – (1 – 2 + 3 – 4 + 5 – 6 + …)
S – B =0+4+0+8+0+12+0+16+0+18……
S – B =4 *(0+1+0+2+0+3+0+4+……)≠4 * (1 + 2 + 3 + 4 + …)
S = 1 +2 + 3 + 4 + 5 + 6 + …
S – B = (1 +2 + 3 + 4 + 5 + 6 + …) – (1 – 2 + 3 – 4 + 5 – 6 + …)
S – B =0+4+0+8+0+12+0+16+0+18……
S – B =4 *(0+1+0+2+0+3+0+4+……)
S – B =4 *((1 – 2 + 3 – 4 + 5 – 6 + …)+(-1+3-3+6-5+3-7+4-9+5-11+6-13+7….))
S – B =4 *(B+(-1+3-3+6-5+3-7+4-9+5-11+6-13+7….))
avec la méthode de l intégrale Antoine, est il possible de déterminer -1+3-3+6-5+3-7+4-9+5-11+6-13+7…. que l on va appeler C?
c=-1+3-3+6-5+3-7+4-9+5-11+6-13+7….
c est une catastrophe.
si A=(-1)^n=+1-1+1-1….. alors S=n=0+1+2+3….. ≠+1+2+3…..
sa fait toute la difference.
le terme n n est pas opérable avec n plus 1.
règle de commutation, permutation pour les sommes infini.
je repose la question n est il un entier naturel ou un entier naturel exclus de zéro?
il faut fixer les réglés et surtout ne pas changer les réglés en cours de partie.
parce que si n est un entier naturel exclus de zéro alors A=-1/2 c est pas pareille que A=1/2.
« n » peut prendre les toutes les valeurs 0, 1, 2, 3 etc …
(-1)^n = 1 pour n=0, puissance 0 de n’importe quel nombre donne toujours 1.
(-1)^n = -1 pour n=1
(-1)^n = 1 pour n=2
etc …
Mais dans les suites et les séries, quelques fois n commence à 0 et d’autres fois il commence à 1, c’est un peu de la cuisine …
Si cette série commençait par -1, il faudrait prendre n commençant par 1 pour que le premier terme soit >0.
Euh je voulais dire <0 …
Au fait, j’ai trouvé une solution à la série de Ramanujan S= 1+2+3+4 … =-1/12, du même tonneau sans passer par les sommes S-B etc … mais elle est tellement biscornue que je me demande moi-même comment je suis arrivé à un résultat juste avec des hypothèses bancales …
Je mettrais ça plus tard, après vérification.
Juste une chose que j’ai comprise en cherchant les solutions et qu’il faut avoir à l’esprit :
On raisonne de manière scolaire en termes d’opérations, d’additions, soustractions etc … mais ces séries dites « infinies » ne sont pas des opérations, des additions ou des soustractions « normales », on peut pas faire ce qu’on veut avec, regrouper les termes, mettre des parenthèses etc… sans changer la valeur totale de la série.
En fait ces séries sont des « fonctions » à la différence près qu’elles ne sont définies que sur des points n; une des preuves de ce que j’avance est qu’on passe par des sommes partielles de la série comme quand on calcule le y(x) d’une fonction pour un x donné, donc tenter de faire la somme totale (et impossible) ne sert à rien, il faut raisonner autrement, d’où toutes les astuces pas évidentes que l’on voit pour trouver des solutions …
j attend avec impatience.
S=1+2+3+4+5….
S=(-1+1-1+1…)*(-1+2-3+4…)
S=(-1/2)*(-1/4)
S=1/8
S=A*B
∑n=∑(-1)^n)×∑n*(-1)^n)
∑n=∑(-1)^n)×n*(-1)^n)
∑n=∑n*1
∑n=∑n
c est pour prouver que A*B est egal a S
S=A*B a condition que n soit un entier naturel ou zero est exclus.
avec les entier naturel,c est a dire en comptant a partir de zero S≠A*B
d ou l importance de savoir a l avance si n est un entier naturel ou un entier naturel ou 0 est exclus.
attention je ne suis pas sure que pour B=-1+2-3+4-5+6… =-1/4
a reverifier avec la methode integrale d antoine.
oups j ai encore parler trop vite
S=A*B meme si n commence a partir de 0
Une autre solution originale à la série de Ramanujan S= 1+2+3+4+5 … = -1/12
J’ai décomposé la série S= 1+2+3+4+5 … en deux
S+= +1_+3_+5_ …
S-= _ -2_ -4_ -6 …
Les termes de la suite S, n0, n1, n2, n3 … prennent respectivement la valeur +1, -2, +3, -4 …
Les termes impairs ont été artificiellement multipliés par -1 pour le tracé de deux courbes séparées
Tous les points somme de la suite S+ sont contenus dans une courbe de type y(x)= x^2
Tous les points somme de la suite S- sont contenus dans une courbe de type z(x)= -x^2+k
J’ai procédé au même changement de variable « x » avec x= 1/2n+1 pour calculer k=1/4
J’ai prolongé les deux courbes jusqu’à x = -2 pour voir que les deux courbes se croisent et se recoupent en deux points : x^2 = -x^2+1/4, soit x = √(1/8) et x = -√(1/8)
En intégrant la somme des deux courbes entre ces deux bornes x = √(1/8) et x = -√(1/8)
∫ y(x) + z(x) dx= 1/3.x^3 +1/3.x^3-x/4 = -√(2)/12
Puis en divisant par 2 et par 2.√(1/8) le résultat on trouve S= -1/12
Ça demande encore à être creusé mais ça semble fonctionner …
Une nouvelle solution originale à la série de Ramanujan S= 1+2+3+4+5 … = -1/12
J’ai trouvé une solution plus simple encore mais je ne sais pas encore comment l’interpréter :
Je décompose la série S= 1+2+3+4+5 … en deux mais sans changer le signe
Sa = +1_+3_+5_ …
Sb = _ +2_ +4_ +6 …
Les termes de la série S, n0, n1, n2, n3 … prennent respectivement la valeur +1, +2, +3, +4 …
Tous les points somme de la série Sa sont contenus dans une courbe y(x)= x^2
Tous les points somme de la série Sb sont contenus dans une courbe z(x)= x^2-1/4
La courbe z(x) s’annule pour x = -1/2 et x= 1/2 et devient négative entre ces deux bornes
En intégrant la somme des deux courbes entre x = -1/2 et x = 1/2
∫ y(x) + z(x) dx= 1/3.x^3 +1/3.x^3-x/4
On trouve directement S = -1/12 !!!
La solution se simplifie mais le mystère reste entier …
attention antoine.
A=1-1+1-1+1…
A=(1+0+1+0+1…)+(-0-1-0-1-0-1)
ce n est pas la meme chause que.
A=(1+_+1+_+1+_…)+(-1-_-1-_-1-_…)
ce n est pas une fatalite pour autant.
attention antoine.
A=+1-1+1-1+1…
A=(+1+0+1+0+1…)+(-0-1-0-1-0-1)
ce n est pas la meme chause que.
A=(+1+_+1+_+1+_…)+(-_-1-_-1-_-1-_…)
ce n est pas une fatalite pour autant.
B = 1 – 2 + 3 – 4 + 5 – 6 + 7 – …
B = (-1+1-1+1-1….)+(+2-3+4-5…)
se n est pas la même chausse que
B = 1 – (2 – 3 + 4 – 5 + 6 – 7 +…)
https://fr.wikipedia.org/wiki/S%C3%A9rie_(math%C3%A9matiques)#Les_s.C3.A9ries_ne_sont_pas_vraiment_des_sommes
https://fr.wikipedia.org/wiki/Famille_sommable
je pense qu il faut savoir si les règles de commutativité et d’associativité ont bien été définit (ou pas) pour l ensemble des Somme (arithmétique).
auquel cas il va falloir définir une convention pour les règles de commutativité et d’associativité a l ensemble des Somme (arithmétique).
A=+1-1+1-1+1…
A=(+1+0+1+0+1…)+(-0-1-0-1-0-1…)
A=A+ + A-
y(n)=5/4×n+3/4
z(n)=-5/4×n-1/4
∫ y(n) dn= 5/8×n^2+3/4×n
∫ z(n) dn= -5/8×n^2-1/4×n
Σ ∫ y(n) + ∫ z(n) =5/8×n^2+3/4×n+(-5/8×n^2-1/4×n)=n/2
celle ci me plais d avantage.
par contre pour trouver dirrectement S sa doit pas être évident.
encore oups petite erreur.
A=+1-1+1-1+1…
A=(+1+0+1+0+1…)+(-0-1-0-1-0-1…)
A=A+ + A-
y(n)=1/2×n+3/4
z(n)=-1/2×n-1/4
∫ y(n) dn= 1/4×n^2+3/4×n
∫ z(n) dn= -1/4×n^2-1/4×n
Σ ∫ y(n) + ∫ z(n) =1/4×n^2+3/4×n+(-1/4×n^2-1/4×n)=n/2
celle ci me plais d avantage.
par contre pour trouver dirrectement S sa doit pas être évident.
S(n)=+1+2+3+4+5…≔Σn
S(n)=A(n)×B(n)=(-1+1-1+1…)×(-1+2-3+4…)≔∑(-1)^n)×∑n*(-1)^n)
S(n)=((A-) + (A+))×((B-)+(B+))=((-1-0-1-0…)+(+0+1+0+1…))×((-1-0-3-0-4…)+(+0+2+0+4+0+…)≔
j ai écris volontairement S(n) comme une fonction de n.
les séries sont les point par lesquels les fonctions doivent obligatoirement passer. exemple : +1+2+3+4+5
je dis bien les fonctions car nous ne connaissons pas les valeurs intermédiaire a ces points.
il y a donc une infinité de valeur donc une infinité de fonction.
pour être encore plus rigoureux.
il n existe peut être pas une infinité de fonction A(n)=(A-(n))+(A+(n)) vrais sur l ensemble des réels voir des imaginaires.
quel sont donc ces fonctions?
S(n)=+0+1+2+3..
S(n)=(+1-1+1-1..)×(+0-1+2-3..)
S(n)={(+1+0+1+0..)+(-0-1-0-1..)}×{(+0+0+2+0+4..)+(-0-1-0-3..)}
S(n)=S(n)
S(n)=A(n)×B(n)
S(n)={[A+(n)] + [A-(n)]}×{[B+(n)] + [B-(n)]}
S(n)=n
S(n)=(-1)^n)×n×(-1)^n)
S(n)={(1+(-1)^n)/2+(-1+(-1)^n)/2}×{((1+(-1)^n)/2)×n+((-1+(-1)^n)/2)×n}
∑S(n)=+0+1+3+6+10..
∑S(n)=(+1+0+1+0..)!×!(+0-1+1-2+2-3+3..)
∑S(n)={(+1+1+2+2+3+3..)+(-0-1-1-2-2-3-3)}!×!{(+0+0+2+2+6+6+12..)+(-0-1-1-4-4-9..)
j ai mis un point d exclamation a la multiplication sa coince.
∑S=+0+1+3+6+10..
https://fr.wikipedia.org/wiki/Nombre_triangulaire
sa peut peut être ouvrir une piste.
https://fr.wikipedia.org/wiki/Encyclop%C3%A9die_en_ligne_des_suites_de_nombres_entiers
encore très intéressant.
http://oeis.org/
complètement dingue ces mathématiciens.
A=+1-1+1-1…=1/2 Série de Grandi https://fr.wikipedia.org/wiki/S%C3%A9rie_de_Grandi
-A=-1+1-1…=-1/2
C=+1+1+1+1…=-1/2 https://fr.wikipedia.org/wiki/1_%2B_1_%2B_1_%2B_1_%2B_%E2%8B%AF
-C=-1-1-1-1-1…=1/2
donc.
+1-1+1-1…=-1-1-1-1… et aussi -1+1-1+1…=+1+1+1+1…
encore une diablerie.
y a pas un moyens de passer les sommations a la moulinette deep learning.
après tout c est bien la fonction du cerveau de mètre de l ordre a se qui semble ne pas l être.
yesssssss
https://fr.wikipedia.org/wiki/Nombre_triangulaire
pour la fonction du Nombre_triangulaire quant n est égal a -1/2 sur l axe des ordonnée j ai -1/8
S=1+2+3+4+5….
S=(-1+1-1+1…)*(-1+2-3+4…)
S=(-1/2)*(-1/4)
S=1/8
haaaa on va bien finir par trouver une explication cohérente.
bon j ai trouve se fameux -1/12
c est l intégrale de la fonction t(n) du nombre triangulaire sur l intervalle a=-1 b=0.
t(n)=(n(n+1))/2=(n^2+n)/2=1/2n^2+1/2n
T(n)=1/6n^3+1/4n^2
∫t(n) dn=T(a)-T(b)=-1/12
comme je suis nul en intégrale et que pour le coups la fonction est sous l axe des abscisse je prend une fonction qui se trouve au dessus de l axe des abscisse et qui a la même aire sur l intervalle a=0 b=1.
rebelotte.
t(n)=1/2n-1/2n^2
T(n)=1/4n^2-1/6n^3
∫t(n) dn=T(a)-T(b)=1/4-1/6=1/12
corrigez moi si je me suis trompe je ne connait pas trop les formes d écriture exacte en math.
comme -1/12 est une aire vous faite la moyenne de l aire et vous trouvez -1/4.
utilisez -1/4 pour calculer les dimensions et vous trouvez 10 dimensions comme pour la théorie les cordes actuelle.
-1/4 en ordonnée.
Je suis d’accord.
PS: Tout ce que je dis doit être considéré comme faux
David, il faut fermer les commentaires, ça n’est plus sérieux !
Je pense quand attribuant une valeur positive à S1=1/2, utilise l’axiome du choix dénombrable (1/2 plutôt que -1/2)
Pour calculer S2=1/4 on utilise l’axiome du choix lié ( (1/2)^2 plutôt que (1/2.i)^2)
Les 2 méthodes sont stables et linéaire et régulière car Axiome du choix lié implique l’axiome du choix dénombrable.
Donc S3=-1/12 est la méthode linéaire et réguliére la moins instable.
Bonjour
Je ne me qualifie pas de scientifique ni mathématicien
cela dit j’ai une question à vous poser qui me travaille
est il possible de démontrer rigoureusement que la somme des entiers naturels jusqu’à l’infini est égale à un demi ?
cad avec exactitude
Bien à vous
François
Ben non, puisque tous ça c’est un attrappe nigaud .. on peut démontrer de la même manière que celle i utilisé pour cette supercherie que 1 = 2 , que 2 = 3 et ainsis de suite et donc par récurrence que tous les nombres entiers sont égaux, et qu’il n’y en a donc finalement qu’un seul !
A partir du momemt où le procédé parvient aune telle absurdité, alors il fait une preuve :celle d’être totalement faux. En fait il s’agit d’un abus « d’écriture » mathématique qui conduit à l’erreur car écrire parexemple S = 1 +2 + 3 + 4 + 5 + 6 + … est fautif lespetits points à la fin de cette égalités ne sont pas un objet mathématique, ils ne veulent rien dire !
Alors partir d’un écriture fautive et pour le moins fantaisiste conduit forcément à des calculs qui le font tout autant
CQFD
à bon ils ne veulent rien dire ?? ils signifient une suite de nombre entiers consécutifs 🙂 un nigaud peut corriger un matheux 🙂
Bonjour à tous
Le résultat 1+2+3+4+… = -1/12 est-il absurde ? Ou pas ?
L’histoire des mathématiques a peut-être ici quelque chose d’intéressant à nous dire.
En 1874, quand Cantor formule sa théorie des ensembles et démontre (entre autres) qu’il existe autant d’entiers pairs que d’entiers pairs et impairs réunis, les mathématiciens bien-pensants de son temps, Kronecker en tête (Poincarré lui-même n’en pensait sans doute pas moins) crient à l’absurdité, dénoncent un manque de rigueur, et tentent même de le faire passer pour un fou.
En 1813, quand Gauss hésite à publier ses travaux sur la géométrie non-euclidienne, il redoute de passer pour un fou auprès de ceux qu’il appelle les « Béotiens », c’est-à-dire les mathématiciens bien-pensants de son temps.
En 1545, quand Cardan introduit l’idée d’un nombre qui, élevé au carré, est égal à -1, il passe évidemment pour un fou auprès des mathématiciens bien-pensants de son temps.
Aujourd’hui, ces grands concepts mathématiques que sont les nombres complexes, la géométrie non-euclidienne ou la théorie des ensembles (sans même parler des nombres négatifs fustigés par D’Alembert lui-même) sont parfaitement compris et admis par tous les mathématiciens, malgré leur caractère a priori absurde.
L’histoire nous appelle donc à la prudence. Evitons les jugements à l’emporte-pièce face à ce qui nous paraît a priori absurde. Gardons-nous d’être les Béotiens de notre temps en affirmant que 1+2+3+4+… ne peut pas être égal à -1/12 !…
A=1-A’
n……………n+1
Σ(-1)^k=1-Σ(-1)^k
k=0………..k=0
1=1-0 ⇒n=1
0=1-1⇒n=2
A≠A’
————————————————–
B=1-B’-A
n……………………..n+1…………….n
(Σ(k+1)(-1)^k)=1-(Σ(k+1)(-1)^k)-Σ(-1)^k
k=0…………………..k=0…………….k=0
1=1+1-1⇒n=1
-1=1-2-0⇒n=2
2=1+2-1⇒n=3
-2=1-3-0⇒n=4
B≠B’
—————————————————
S’=B »+4S
2(n+1)….2(n+1)…………..n
(Σk+1)=(Σ(k+1)(-1)^k)+4Σk+1
k=0……..k=0……………….k=0
3=-1+4×1⇒n=1
10=-2+4×3⇒n=2
21=-3+4×6⇒n=3
36=-4+4×10⇒n=4
S’≠S
—————————————————-
Pour préserver l’ égalité je suis obliger de modifier la limite supérieure de sommation.
https://fr.wikipedia.org/wiki/Somme_(arithm%C3%A9tique)#Notation
comme la démonstration de 1+2+3+4+…=-1/12 se fait en trois étapes, il ne m’est pas possible de montrer les erreurs d’un seul tenant.
Un exemple plus flagrant d’erreur du au non respect de la limite supérieure de sommation.
1+2+3+4+…=-1/8 https://www.youtube.com/watch?v=EfR9KCX91dM
Explication dans les commentaires.
vidéo bonus intéressante aussi. https://www.youtube.com/watch?v=BpfY8m2VLtc
Cordialement.
Thomas GUITARD
A=1-A’
n……………n+1
Σ(-1)^k=1-Σ(-1)^k
k=0………..k=0
1=1-0 ⇒n=1
0=1-1⇒n=2
A≠A’
————————————————–
B=1-B’-A
n……………………..n+1…………….n
(Σ(k+1)(-1)^k)=1-(Σ(k+1)(-1)^k)-Σ(-1)^k
k=0…………………..k=0…………….k=0
1=1+1-1⇒n=1
-1=1-2-0⇒n=2
2=1+2-1⇒n=3
-2=1-3-0⇒n=4
B≠B’
—————————————————
S’=B »+4S
2(n+1)….2(n+1)…………n+1
(Σk+1)=(Σ(k+1)(-1)^k)+4Σk+1
k=0……..k=0……………….k=0
3=-1+4×1⇒n=0
10=-2+4×3⇒n=1
21=-3+4×6⇒n=2
36=-4+4×10⇒n=3
S’≠S
—————————————————-
Pour préserver l’égalité je suis obligé de modifier la limite supérieure de sommation.
https://fr.wikipedia.org/wiki/Somme_(arithm%C3%A9tique)#Notation
Comme la démonstration de 1+2+3+4+…=-1/12 se fait en trois étapes, il ne m’est pas possible de montrer les erreurs d’un seul tenant.
Un exemple plus flagrant d’erreur du au non respect de la limite supérieure de sommation.
1+2+3+4+…=-1/8 https://www.youtube.com/watch?v=EfR9KCX91dM
Explication dans les commentaires.
vidéo bonus intéressante aussi. https://www.youtube.com/watch?v=BpfY8m2VLtc
Cordialement.
Thomas GUITARD
Pourquoi t’essayes de nous carotte ?
Pingback: Maths | Pearltrees
Pingback: Supérieur | Pearltrees
LA DIMENSION DE L’UNIVERS GENERALISE EST 6 – DEMONSTRATION
Pour rappel, l’Univers Généralisé est la Réunion de tous les Univers Multiples et de leurs Univers Parallèles et du temps. L’Univers Généralisé est un Espace Mathématique de dimension 6, en effet ceux-ci sont :
Les axes X, Y et Z du repère Héliocentrique ou repère de Copernic centré sur le Centre d’Inertie du Soleil et ses 3 axes orthogonaux X, Y et Z qui sont orientés vers 3 étoiles fixes de notre Univers Multiple, ils constituent à eux seuls 3 DIMENSIONS,
Le temps t constitue 1 Dimension,
L’indice de l’Univers Multiple qui constitue 1 DIMENSION, l’indice N varie de 1 à l’infini,
L’indice de l’Univers Parallèle indice M constitue la 6ème DIMENSION, M varie de 1 à P avec P fini ou infini.
L’Univers Généralisé comporte un point d’origine 0 qui est le Centre de Gravité de notre Soleil et 6 axes dans un espace vectoriel d’ordre 6, il constitue un Vecteur Uni Colonne qui possède 6 composantes dans l’ordre suivant :
– Première Composante, l’abscisse X,
– Deuxième Composante, l’ordonnée Y,
– Troisième Composante, la cote Z,
– Quatrième Composante, le temps t,
– Cinquième Composante l’indice N de l’Univers Multiple considéré,
– Sixième Composante l’indice M de l’Univers Parallèle de l’Univers Multiple N.
Pour plus d’information se reporter à l’Article Scientifique intitulé THEORIE DE L’INFINI VERSION ALAIN MOCCHETTI qui explicite ce que sont les Univers Multiples et à l’Article Scientifique intitulé UNIVERS PARALLELES – DEFINITION qui explicite en profondeur ce que sont les Univers Parallèles. 2 possibilités d’accès sont à votre disposition, à savoir :
– Consulter Mon Journal Scientifique DAVID MOCCHETTI qui est gratuit, aller à l’Article ASTROPHYSIQUE – RECAPITULATIF GENERAL,
– Taper (Alain Mocchetti Ingénieur) dans le moteur de recherche de Google https ://www.google.fr/ et effectuer un second tri.
Si vous ne trouvez pas, prière de me contacter sur le Messenger du Compte Facebook DAVID MOCCHETTI ou envoyer un email à alainmocchetti@gmail.com.
Soit le Vecteur (3, 85.102.3500, 1, 10) il correspond à la position d’un Corps Céleste avec (X,Y,Z) = (53,85,102) en mètre, t = 3500 secondes, Univers Multiple numéro 1, Univers Parallèle numéro 10 de l’Univers Multiple numéro 1.
Alain Mocchetti
Ingénieur en Construction Mécanique & en Automatismes
Diplômé Bac + 5 Universitaire (1985)
UFR Sciences de Metz
alainmocchetti@sfr.fr
alainmocchetti@gmail.com
@AlainMocchetti
Au secours Stephen Hawking est ressuscité et il tourne en rond dans la sixième dimension sans se rendre compte qu’il s’est gouré de blog …
Encore la Antoine.
Mais non c’est David_Hilbert.
Ok dans le même raisonnement:
Posons alors A = 1 + 2 + 3 + ….
On a -2*A = -2 -4 -6 +….
Soit A -2A + A= 1 + 2 + 3 + 4 + 5 + …
-2 -4 -6 -8 + …
+1 +2 +3 +…
Donc 0 = A – 2A + A = 1 + 0 + 0 + 0 = 1
Donc 1 = 0
La consistance de cette méthode me plait.
Au moins, il y a des interrogations et de la réflexion. Ne rien rire, ne rien faire, c’est commode.
Il y a quand même plus des premières que de la seconde… mince faut faire des sommes partielles alors ? ^^
Bonjour à tous et merci à David pour son super blog et la qualité / quantité de son travail.
David a écrit « […] si on respecte quelques règles élémentaires, quelle que soit la manière dont on s’y prend, on trouve que si on veut affecter une valeur finie à cette somme monstrueuse, alors -1/12 est l’unique valeur qui colle. »
Si j’ai bien compris, on cherche un procédé de sommation S sur un espace H de suites. On voudrait que S soit défini pour la suite a=(1;2;3;…) et on affirme qu’alors nécessairement S(a)=-1/12 si des « règles élémentaires » sont respectées.
En relisant les calculs de David ainsi que son deuxième billet de blog sur ce sujet, on voit que ces règles sont, au minimum:
1) S linéaire sur H
2) S (u) = u_0 + S (T (u)) où T(u) est la suite u translatée d’un indice vers la gauche.
3) T (u) appartient à H (pour que 2) ait du sens); plus précisément H stable par T.
Mais si on pose b=T(a)=(2;3;4;…) et c=T(b)=(3;4;5;…) alors, on obtient
S(a+c-2b)=S(0;0;0;…)=0 par linéarité de S
Donc, toujours par linéarité, 0 = S(a) + S(c) -2 S(b) = 1 + 2 + S(c)+ S (c) – 2 (2 + S(c)) = -1
Patatra !
Sans même exiger que le procédé S coïncide avec la sommation usuelle sur les séries convergentes, on voit que ce que cherche David n’existe pas. Autrement dit, il n’existe pas de procédé de sommation permettant de justifier la façon dont on a mené les calculs aboutissant à -1/12 pour la « somme des entiers ». Au passage on en déduit une réponse à une question que se pose David dans son deuxième billet: le procédé de sommation de Ramanujan utilisant la régularisation par la fonction zeta, n’est pas linéaire (puisqu’il donne une valeur à la somme des entiers et que l’espace des suites sommables pour ce procédé est stable par T).
Bien évidemment, je ne suis pas en train de dire qu’il n’existe pas de procédé de sommation permettant de donner un sens à la « somme des entiers » . Non, je dis juste que dans le billet de David, il faut corriger quelques phrases dont la première que j’ai citée (ou alors la préciser davantage) trop affirmative et trop imprécise à la fois.
En fait si on veut corriger un peu ce qui est dit, malheureusement il reste peu de choses à dire. On peut dire qu’il existe un procédé de sommation qui donne un sens à la somme des entiers (la régularisation zeta) et que le résultat de ce calcul peut servir de manière Olé Olé à justifier des résultats d’une expérience en physique.
Et justement il y a un autre problème plus fondamental et qui me gène dans ce qui est proposé ici. La sommation que souhaite David est totalement étrangère à la notion de convergence (pas de topologie ici). Elle est aussi totalement étrangère à la notion de commutativité. Or, dans le phénomène de Casimir, ces deux notions sont bien présentes. C’est à dire que si le physicien mesure l’énergie dans un ordre différent, il devrait trouver le même total. Et il souhaite bien *approcher* un calcul d’énergie. Les concepts de commutativité et de convergence sont donc là.
Je vais exprimer un sentiment qui n’engage que moi : si ce billet sème autant la controverse ce n’est pas parce que les lecteurs sont tous bornés ou coincés, c’est aussi parce que je crois qu’il manque beaucoup plus de rigueur et de prudence que les autres billets de ce blog.
Avec tout mon respect,
Cyril
Pingback: Http://www.pearltrees.com/u/47122352-liste-discussion-diffusion#l665 | Pearltrees
Pingback: Manca Giuda! | Moselleorthodoxe's Blog
Pingback: Et bîîîîîîîîîîm! – Comfortably Numb
Bonjour,
Merci pour cet article quelque peu déconcertant
Juste une question qui n’a rien avoir avec le contenu, mais concerne WordPress.
Quel plugin utilisez-vous pour la gestion des abonnements ?
Merci et encore merci pour nous faire nous partager vos connaissances
WOAW eh ben ! ça a du être chiant à écrir tou ça !
1+2+3+4+5+6+7+… = ∞ * ((∞+1)/2))
1+2+3+….+n=n((n/2)+(1/2))
Je ne suis pas plus qualifié que cela mais je pense que le biais de la démonstration se situe ici:
A = 1 – 1 + 1 – 1 + 1 – … = 1 – (1 – 1 + 1 – 1 + 1 – …)
Appelons A’ le terme situé à gauche de cette égalité tel que:
A’ = 1 – (1 – 1 + 1 – 1 + 1 – …)
L’égalité s’écrit donc:
A = A’
Or, la suite A comporte 5 occurrences de « 1 » alors que la suite A’ en comporte 6.
Ce qui laisse penser que la suite A’ est plus avancée dans le temps que sur la suite A (Si les suites A et A’ croissaient au même rythme (posons chaque seconde) alors A serait à 4 secondes et A’ à 5 secondes).
Vous égalez donc 2 suites semblables MAIS qui sont dans 2 états (ou temporalités) différents, ce qui n’est à mon sens pas très « rigoureux ».
Plus rigoureusement, il aurait fallu écrire:
A = 1 – 1 + 1 – 1 + 1 – … = 1 – (1 – 1 + 1 – 1 – …)
… mais on ne reconnaîtrait alors plus A dans le terme entre parenthèses…
Bravo pour vos blog et vlog,
Cordialement.
mmm…
comprendre: « Appelons A’ le terme situé à gauche de cette égalité » remplace par « Appelons A’ le terme situé à droite de cette égalité »
Il faut savoir que les mathématiques se base sur des axiomes que l’on considère comme « juste ».
Là, on peut remettre en question les axiomes des mathématiques que l’on connait mais aussi (d’après moi), considérer qu’elles restent justes mais sans pour autant n’avoir qu’une seule réponse possible et donc avoir plusieurs résultats possibles selon l’interprétation que l’on en fait.
(quand je parle de plusieurs résultats possibles, je parle de résultats différents avec une logique différente comme 1+2+…+n = +inf ou -1/12. Je considère par exemple que le fait que x² = 4 a comme solution possible -2 ou 2 n’est qu’un seul résultat vu que ça reste dans une même logique. Je n’ai juste pas assez de vocabulaire mathématiques)
Remarque : mes connaissances en maths restent limités au lycée, un peu aux études supérieurs (informatique) et à ce que j’ai vu sur internet donc n’hésitez pas à me reprendre si je dis des absurdités 🙂
Je suis un total ignorant (je me suis arrêté au niveau 3e collège, à peu près, en mathématiques). Mais je voudrais juste vous poser deux questions : 1ère question : un « nombre » et une « formule » est-ce la même chose ? un nombre est fini (écrit, arrêté dans le temps), une « formule » est infinie, dynamique : une « sorte de processus continuel de générations de nombres » : c’est comme si l’on prend une imprimante de supermarché à rouleau qui imprimerait des additions sans jamais s’arrêter : donc elle ne tracerait jamais la ligne du total : donc nous n’aurions alors aucun nombre déterminant le total : comment pourrait-elle écrire un nombre (que ce soit -1/12 ou tout autre nombre) alors qu’elle continue d’additionner ? Il faudrait qu’elle s’arrête pour nous donner un nombre représentant le total. Mais elle ne s’arrêtera jamais car elle additionnera pour toujours (car l’infini ne finit pas). Elle ne passera jamais le stade de « faire le total » car elle n’arrêtera jamais le stade d’additionner. 2ème question : l’égalité (le signe =) ne s’applique-t-il pas uniquement sur des nombres finis et non pas sur des « formules » ? Une égalité n’est possible que dans un monde non-dynamique (arrêté dans le temps) : le signe « = » ne se place qu’entre deux nombres arrêtés dans le temps (et non pas en train de se former). En parlant d’égalités et de nombres, j’ai l’impression que l’on applique des propriétés non-dynamiques à quelque chose qui est dynamique. Peut-on appliquer à des concepts dynamiques des propriétés propres à des concepts non-dynamiques ? Qu’en pensez-vous ? Merci pour votre (vos) réponse(s). Merci à Science étonnante !
Plus simplement :
A = 1 – 1 + 1 – 1 + 1 – … (1)
ce qui peut se réécrire, comme vous l’avez fait, en :
A = 1 – ( 1 – 1 + 1 – 1 + … ) (2)
Introduisons une quantité X telle que :
A = 1 – X (3)
et remarquons par simple association que X est égal au terme entre parenthèse dans (2)
Votre erreur vient d’avoir assimiler le terme entre parenthèse dans (2) à A alors que sa valeur est X !
Cela vient d’une erreur de notation.
Vous auriez dû symboliser les termes de votre équation initiale (1) comme dans (1′) :
A = 1 – 1 + 1 – 1 + 1 – … (1)
A = t(0) + t(1) + t(2) + … + t(∞) (1′)
Puis votre réécriture serait devenue :
A = 1 – ( 1 – 1 + 1 – 1 + … ) (2)
A = t(0) – ( – t(1) – t(2) – … – t(∞) ) (2′)
Dans cette écriture, il n’est plus possible d’assimiler le terme entre parenthèse dans (2′) à A
ce qui serait doublement hasardeux puisqu’il manque t(0) et que tous les autres termes sont négatifs !
On reconnaît facilement que le terme entre parenthèse dans (2′) vaut par définition :
t(0) – A (3′) (qui est aussi égal à notre X plus haut)
et donc on peut seulement réécrire (2) en :
A = t(0) – ( t(0) – A )
c’est-à-dire la trivialité suivante :
A = A
ce qui n’a rien d’étonnant puisqu’aucune composition n’a été effectuée par aucun axiome ou théorème.
Pour aller plus loin, il serait nécessaire d’introduire quelques informations comme :
t(i) = 1 pour tout i pair
t(i) = – 1 pour tout i impair
En rassemblant les t(i) pairs d’un côté et les t(i) impairs de l’autre, il vient :
A = ( t(0) + t(2) + … ) – ( – t(1) – t(3) – … )
ou plus exactement :
A = ( t(0) + t(2) + … + t(n) ) – ( – t(1) – t(3) – … – t(n-1) ) si n est un infini pair !
A = ( t(0) + t(2) + … + t(n-1) ) – ( – t(1) – t(3) – … – t(n) ) si n est un infini impair !
Mais comme la notion d’infini pair ou impair n’est ni définie ni définissable, on devrait en conclure logiquement que la valeur de A est indéfinie. Ce qui est conforme à l’intuition initiale de tout bon mathématicien, non ?
Bonne analyse.
Je ne suis pas mathématicien.
Pour moi se fameux -1/12 ne fait pas partie de la branche des mathématiques du fini.
C est une autre façon de faire des calculs avec des règles différentes ou ∞+1=∞
Je pense que ces deux branches des mathématiques n ont pas été suffisamment distincte, définit, se qui mène a la confusion.
Cordialement,
Thomas.
Salut David ! Merci pour cet enrichissement .
Bien sûr la somme des nombres entiers ne vaut pas -1/12 !
C’est juste que pour prolonger la fonction zêta de Riemann sur C , il faut nécessairement que ce prolongement ait cette valeur pour cette somme ( analogie avec le prolongement de la notion de somme de séries sous certaines conditions ) ! Donc -1/12 n’est pas la valeur de zêta pour cette somme ; mais plutôt la valeur du prolongement de zêta pour cette somme sur C . D’ailleurs ce prolongement est défini sur tout C sauf pour la somme harmonique . Il s’agit donc d’un abus de langage .
Maintenant , un tel lien n’est vraisemblablement pas dépourvu de sens , exemple effet casimir !
Cela pousse à penser que la notion de prolongement par continuité serait un formalisme qui traduirait mathématiquement une réalité physique , assimilable à des changements d’état brusques par exemple ( somme qui passe de l’infini à -1/12 …). Cela donne des idées sur la théorie de la genèse de l’Univers !!
Décidément , l’Infini est loin d’avoir livré tous ses secrets !!!
Bonjour,
Crtitiquer le -1/12 ok, poser qu’il est totalement faux, absurde, incohérent vis à vis de certains référentiels, ok mais par rapport à la théorie des cordes, de la magie du chiffre 12, l’effet Casimir c’est troublant, etc.
Il me semble que ce -1/12 à sa pertinence au sens lourd, profond du terme.
Quant à la réponse d’Aba Bob, je suis tout à fait d’accord avec, elle fait écho à mon propos à une hauteur largement supérieure à-1/12 😄, bref 👍.
Cordialement.
P.S. Pour moi il y a un truc pertinent dans ce -1/12 autrement formulé pour l’humanité cette somme -1/12 est cohérente au même titre que Pi.
Il y a un truc qui m’ échappe. La suite varie de 0 à 1. Donc la valeur max supérieure est 1 et sa moyenne donc est de 1/2. Comment peut on résonner avec une valeur max et une valeur moyenne ?
La repense est peut être la https://fr.wikipedia.org/wiki/S%C3%A9rie_de_Grandi
ou la https://fr.wikipedia.org/wiki/Lemme_de_Ces%C3%A0ro
Se qui est sur c’est que la somme des entier naturels de Ramanujan vous apprendra a connaitre la fonction zêta en deux minutes.
https://www.youtube.com/watch?v=dNpdMYB8pZs
Vous vous apercevrez que l’intégrale de la la série de Grandi sur l’intervalle (-1 0) est égale a 1/2.
f(x) = (cos(x∙3.14116)+1)/2
valable aussi pour le Nombre triangulaire qui est la somme des entier naturel et tous les nombres complexe de la fonction zêta.
https://fr.wikipedia.org/wiki/Nombre_triangulaire
https://fr.wikipedia.org/wiki/Fonction_z%C3%AAta_de_Riemann#Produit_eul%C3%A9rien
Lien qu’il existe entre les nombres premier et les entier naturels.
https://fr.wikipedia.org/wiki/Fonction_z%C3%AAta_de_Riemann#Produit_eul%C3%A9rien
Pourquoi Reimann cherchais il ces fameux zéros non triviaux.
https://www.youtube.com/watch?v=KvculWl-jhE
Si vous dites que A est la somme alternative de 1 et -1, on peut donc dire que A la somme de : la somme de 0 à l’infinie du nombre 1 et de la somme de 0 à l’infini du nombre -1. Or la seconde partie peut mettre -1 en facteur, elle peut donc s’écrire -1 * la somme de somme de 0 à l’infini du nombre 1. Donc A = 0.
Quand vous écrivez que A = 1 – A on en déduit que 0 = 1 ce qui est faux. Vous ne pouvez donc pas écrire A = 1 – 1 + 1 – 1 …
donc A = 1 – (1 – 1 + 1 – 1… ) = 1 – A
dans la somme entre parenthèse il n’y a plus le même nombre de 1 et de -1
Si on raisonne avec les suites:
Posons S0 = 0 et Sn = S(n-1) + n
Nous avons S1 = S0 + 1 = 1, S2 = 3 S2 > S1, S3 = 6 S3, quelque soit n>0 on a Sn – S(n-1) = n > 0. Donc quelque soit n S(n+1) > Sn.
Comme S0 = 0 la somme, quelque soit n>0, des n premiers entiers sera supérieur à 0.
Cette démonstration n’utilise pas l’écriture d’une somme infinie de nombres.
I’d like to find out more? I’d love to find out some additional information.
You can check out Scienforall youtube channel 😉. Lê is the only one, as far as i know, who has studied this theme with all the rigour and details it recquires.
See : https://www.youtube.com/watch?v=Ap10Gb2_wcc
https://www.youtube.com/watch?v=IghfFlXK__U
https://www.youtube.com/watch?v=vMnkmBCvGQc
(you also have Mathologer video: https://www.youtube.com/watch?v=YuIIjLr6vUA. But Lê’s videos are, by far, better in quality and accuracy than Mathologer’s (He has made several mathematics mistakes in his claims) )
en fait, ce n’est pas la démonstration de A= 0.5 qui est fausse, c’est encore avant.
c’est « A =1 – 1 + 1 – 1 + 1….. » qui est faux.
A gauche, on a un nombre, mais pas a droite.
on pourrait toutefois l’écrire si la suite 1 – 1 + 1 – 1 + 1….. était convergente.
Bonjour, et bravo pour votre excellent travail excellent. Je voudrais juste signaler une petite confusion sur la fin, concernant la justification des formules pour l’effet Casimir, en gros tout est correct (la somme -1/12 justifie bien cela) mais la formule intégrale n’est pas valide pour cette somme là. Si vous regardez https://en.wikipedia.org/wiki/Ramanujan_summation, il y a plusieurs définitions équivalentes de la sommation de Ramanujan, et vous utilisez la une forme équivalente de C(1) – qui fonctionne pour la série de terme 1/n par exemple. Mais cette forme simple n’est pas valable pour la « somme des entiers » (l’integrale de x.dx jusque n donne n^2/2 + C, et la différence avec n(n+1)/2 est n/2 + C qui diverge), dans ce cas précis on doit se contenter de C(0) – qui malheureusement est beaucoup plus compliquée.
Bravo pour vos efforts !
commentaire sans grande importance
il y a sans doute une faute de frappe sur « convergence au sens d’Abel de la série entière de \frac{1}{1+x^2}. »
je crois que le carré porte sur (1+x) et pas seulement x : c’est le DSE de 1/(1+x)2
En réalité l’équation: S = B + 4S admet 2 solutions :
– une solution finie qui est -1/12
– une solution infinie +∞. En effet, si on retranche un nombre fini quelconque à +∞, ou si on le multiplie par un nombre fini positif, on obtient encore +∞. Ca marche quel que soit la valeur (finie) de B et (positive et finie) du facteur (ici 4).
Ici on a S > 0 par définition donc la bonne solution est la 2e.
Article passionnant et, comme d’habitude, très pédagogique.
Petite coquille : dans la convergence d’Abel, le deuxième exemple correspond à la série entière de 1/(1 + x)² et pas 1/(1 + x²).