Pierre-Feuille-Ciseaux chez les animaux

Dans notre vision traditionnelle de la compétition entre espèces, les forts dominent les faibles, les gros mangent les petits, les plus adaptés supplantent les moins adaptés. Nous raisonnons intuitivement comme s’il existait une hiérarchie stricte entre les espèces.

Et pourtant parfois, on peut avoir entre espèces des situations identiques à celle du jeu « Pierre-Feuille-Ciseaux » (ou Chifoumi), où la pierre bat les ciseaux, les ciseaux battent la feuille, mais la feuille bat la pierre. Il s’agit d’une hiérarchie cyclique, qui ne permet pas de désigner un vainqueur incontestable. On a Pierre > Ciseaux > Feuille > Pierre.

J’évoquais une situation analogue dans mon billet de la semaine dernière sur le paradoxe de Condorcet. Eh bien dans ce billet-ci, nous allons partir à la recherche de ces espèces qui jouent à « pierre-feuille-ciseaux » dans la nature, une situation qui semble d’ailleurs un facteur important de biodiversité !

De la tactique sexuelle des lézards

Le lézard à flanc maculés est une espèce que l’on trouve en abondance au sud-ouest des États-Unis. Une de ses particularités est qu’il existe chez les mâles trois variétés, qui se distinguent par la couleur de leur gorge, ainsi que par leur comportement sexuel :

• les mâles oranges sont agressifs, et défendent de larges territoires peuplés de nombreuses femelles ;
• les mâles bleus sont calmes, et se contentent de petits territoires et de peu de femelles ;
• les mâles jaunes sont fourbes, et tentent discrètement d’aller féconder les femelles sur les territoires des autres.

Les têtes des trois types de lézards sont représentées ci-contre.

Dans un article publié en 1996 dans Nature [1], deux auteurs ont noté que ces trois variétés de lézards se trouvaient dans une situation de pierre-feuille-ciseaux : les mâles oranges battent les mâles bleus par leur comportement agressif et expansionniste. Mais en voulant défendre un trop grand harem, les oranges se font avoir par les jaunes qui les font cocus. De leur côté, les bleus arrivent à supplanter les jaunes, car ils n’ont qu’un territoire plus petit à protéger pour échapper à la tactique fourbe de ces derniers.

Moralité : Orange > Bleu > Jaune > Orange. Entre ces trois variétés de lézards, tout se passe comme au pierre-feuille-ciseaux !

Chifoumi chez les bactéries

La situation décrite ci-dessus pour les lézards existe aussi chez certaines espèces de bactéries. Par exemple la célèbre Escherichia Coli, qui compose 80% de notre flore intestinale (en photo ci-contre).

Il se trouve que certaines variantes d’E.Coli peuvent produire une toxine, la colicine, qui se trouve être fatale pour ses congénères. Mais il existe aussi des souches d’E.Coli qui sont résistantes à la colicine.

On peut donc considérer 3 variétés : les tueuses (T), qui sécrètent la colicine ; les sensibles (S), qui se font tuer par la colicine ; et les résistantes (R), qui y sont immunisées.

Les tueuses T éliminent les sensibles S grâce à leur toxine. Les sensibles S supplantent les résistantes R, car elles sont capables de croître plus vite. Mais en vitesse de croissance, les résistantes R surpassent les tueuses T, car sécréter la toxine est quand même un handicap pour leur propre développement [2]. On a donc S > R > T > S ! Ces relations ont pu être vérifiées in-vitro [2], mais aussi in-vivo sur des souris portant chacune des souches d’E.Coli [3].

Et cette situation n’est pas unique à E.Coli, elle est susceptible d’apparaître dès que ces conditions génériques sont réunies (production coûteuse de toxine, mécanisme d’immunité).

Pierre-Feuille-Ciseaux et biodiversité

Le jeu du pierre-feuille-ciseaux n’est donc pas qu’une curiosité théorique, il se produit bel et bien dans la nature. Certains auteurs pensent d’ailleurs qu’il est un facteur important de biodiversité. Intuitivement, on comprend bien que si parmi plusieurs espèces en compétition pour les mêmes ressources, aucune ne domine à la fois toutes les autres, on évite une situation d’hégémonie avec une seule espèce survivante.

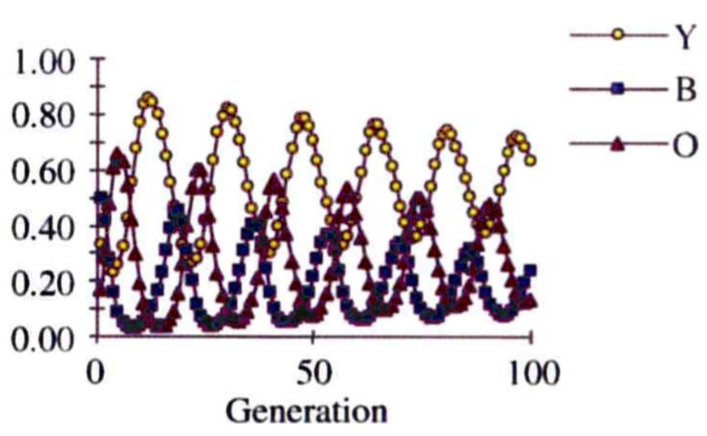
A partir de modèles, les auteurs ont pu vérifier que les situations de pierre-feuille-ciseaux prédisent en fait une oscillation des fréquences différentes espèces, chacune étant capable d’en envahir une autre, mais de se faire envahir par une troisième. C’est ce que montre le graphique ci-contre, extrait de la publi sur les lézards [2], et qui modélise l’abondance relative des 3 variétés en fonction du temps.

Traditionnellement, on explique la biodiversité par le fait que les différentes espèces se développent chacune dans une niche écologique pour laquelle elle est bien adaptée, et que différents environnements conduisent à différentes espèces.

Et pourtant, ce mécanisme n’explique pas ce qu’on appelle parfois le paradoxe du plancton, en référence au fait que dans un environnement en apparence homogène (quelques cm3 d’océan), on peut parfois trouver une immense diversité d’espèces, qui semblent pourtant toutes en compétition pour les mêmes ressources. Le paradoxe du plancton existe aussi sur la terre ferme : un auteur a trouvé dans 30g de terre d’une forêt norvégienne, plus de 500.000 espèces différentes de bactéries ! [4]

Grâce au mécanisme du pierre-feuille-ciseaux, on peut expliquer la biodiversité même dans des environnements homogènes. Toutefois il reste des choses à comprendre, car il a également été montré que cette situation ne se produit que quand les interactions sont locales [2] : si les bactéries croissent sur une plaque, on observe bien la biodiversité et des phénomènes d’invasions multiples, alors que si elles sont toutes mélangées dans une fiole, une des espèces finit par gagner. Pour préserver la biodiversité, il ne faut donc pas trop de mobilité ! [5]

Et pour finir, la variante The Big Bang Theory : le pierre-feuille-ciseaux-lézard-Spock

[youtube=http://www.youtube.com/watch?v=iapcKVn7DdY]

Billet connexes et références :

Robert Axelrod et l’évolution de la coopération

ElJJ sur les dés d’Oppenheimer

[1] B. Sinervo & C.M. Lively, The rock-paper-scissors game and the evolution of alternative male strategies, Nature 380, p240 (1996)

[2] B. Kerr & al., Local dispersal promotes biodiversity in a real-life game of rock–paper–scissors, Nature 418, p171 (2002)

[3] B. Kirkup & M. Riley, Antibiotic-mediated antagonism leads to a bacterial game of rock–paper–scissors in vivo, Nature 428 (2004)

[4] D. Dykhuizen, Why are there so many species of bacteria ? Antonie van Leeuwenhoek 73: 25–33, (1998)

[5] T. Reichenbach et al., Mobility promotes and jeopardizes biodiversity in rock–paper–scissors games, Nature 448, p1046 (2007)

[6] D. Semmann, Volunteering leads to rock–paper– scissors dynamics in a public goods game, Nature 425 p390 (2003)

Pour aller plus loin…

Et chez les humains ? On n’observe pas de chifoumi au sens des espèces, mais cette situation peut se produire dans certains comportements. Un exemple est le jeu dit « des biens publics » (voir la référence [6])

Imaginons par exemple 10 joueurs. A chaque tour, chaque joueur a le choix de donner au pot commun 1€ ou rien du tout. Le pot commun est ensuite multiplié par 5 et redistribué à part égales entre tous les joueurs, indépendamment de leur contribution. Ce jeu symbolise certaines situations de type « passager clandestin », où quelqu’un peut profiter des autres en ne contribuant pas mais en bénéficiant quand même de la redistribution. Avec un jeu de cette forme, la stratégie rationnelle consiste à ne pas contribuer et à se servir sur le dos des autres : en général après plusieurs tours, plus personne ne contribue.

Maintenant ajoutons une variante : avant chaque tour, chaque joueur a la possibilité de passer, c’est-à-dire de ne pas jouer, et de recevoir à la place 1€. Ainsi si trop de monde s’amuse à faire le passager clandestin, vous pouvez plutôt choisir de passer.

Nous avons donc 3 stratégies : contribuer (C), trahir (T) et passer (P).

Nous l’avons vu, la stratégie T finit par supplanter la stratégie C. Mais si tout le monde se met à trahir, vous avez intérêt à passer (stratégie P). Donc la stratégie P domine la stratégie T. Enfin imaginons que parmi les 10 participants, 8 aient décidé de « passer », alors vous avez intérêt à jouer et à mettre 1€, car même si l’autre joueur trahit, vous toucherez au minimum 5€ divisé par 2, ce qui est plus que ce que vous toucherez si vous passez. La stratégie C supplante la stratégie P.

En définitive, on a là-aussi T > C > P > T. Dans une situation d’expérience en labo avec des vrais gens, les auteurs du papier [6] ont pu vérifier que cela produisait aussi des oscillations dans les fréquences des différentes stratégies, et convergeait vers une situation de « biodiversité » avec une proportion égale des 3 stratégies !