 Dans le 3ème épisode de la série Destination Finale, la Mort attrape ses malheureuses victimes lors d’un tour de grand huit mémorable. Précisément dans ce billet, nous allons voir pourquoi en allant dans un looping de montagnes russes, vous ne devriez en théorie passer pas si loin de la mort…
Dans le 3ème épisode de la série Destination Finale, la Mort attrape ses malheureuses victimes lors d’un tour de grand huit mémorable. Précisément dans ce billet, nous allons voir pourquoi en allant dans un looping de montagnes russes, vous ne devriez en théorie passer pas si loin de la mort…
Pour élucider la physique du looping, nous allons simplement nous demander quelles sont les conditions nécessaires pour ne pas tomber une fois en haut de la boucle.
Ce petit calcul sera l’occasion de réviser deux ou trois principes de base de mécanique, ce qui est tout de même mieux que de regarder Destination Finale 3.
Première condition : ne pas tomber une fois en haut
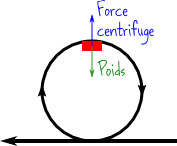 Vous êtes vous déjà demandé pourquoi on ne tombe pas dans la boucle d’un looping ? Vous savez, à ce moment exact où vous êtes pile la tête en bas ? La réponse, c’est la force centrifuge ! Quand vous êtes en haut du looping, vous suivez une trajectoire circulaire, et la force centrifuge vous pousse à l’extérieur de cette trajectoire. Et dans ce cas précis, elle vous pousse vers le haut !
Vous êtes vous déjà demandé pourquoi on ne tombe pas dans la boucle d’un looping ? Vous savez, à ce moment exact où vous êtes pile la tête en bas ? La réponse, c’est la force centrifuge ! Quand vous êtes en haut du looping, vous suivez une trajectoire circulaire, et la force centrifuge vous pousse à l’extérieur de cette trajectoire. Et dans ce cas précis, elle vous pousse vers le haut !
Faisons un bilan : au moment où vous êtes au sommet, vous subissez deux forces : la gravité qui vous emmène vers le bas, et la force centrifuge qui vous pousse vers le haut. Pour ne pas tomber, il faut tout simplement que la force centrifuge compense la gravité !
Je ne sais plus si on apprend ça au lycée, mais peut être savez vous comment on calcule la force centrifuge que l’on subit dans une trajectoire courbe, il s’agit de
\(F = m \frac{v_H^2}{R}\)
où \(m\) est votre masse, \(v_H\) votre vitesse en haut du looping, et R le rayon de courbure de la trajectoire : ici c’est le rayon de la boucle. Donc pour que la force centrifuge au sommet de la boucle soit au moins égale à votre poids, il faut
\(m \frac{v_H^2}{R} = mg\)
où bien sûr \(g=9.81 m/s^2\) est l’accélération de la pesanteur. Votre vitesse doit donc être d’autant plus élevée que la boucle est grande.
Deuxième condition : arriver jusqu’en haut !
Nous venons de voir que pour survivre à un looping, il faut que vous ayez une vitesse suffisante en haut. Mais puisque votre vitesse va diminuer quand vous aller grimper le long de la boucle, il faut que votre vitesse en bas soit encore plus élevée ! Mais de combien ?
Le calcul est simple : Pour passer du bas au haut de la boucle, vous vous élevez d’une hauteur égale à 2 fois le rayon R de la boucle. Votre énergie potentielle de pesanteur augmente donc de la quantité \(mg*2R\). En appliquant le théorème de l’énergie cinétique, on trouve la relation entre votre vitesse en haut et votre vitesse en bas de la boucle
\(\frac{1}{2}mv_B^2 – \frac{1}{2}mv_H^2 = 2mgR \)
Si vous combinez cette égalité avec la condition qu’on a trouvé pour ne pas tomber une fois en haut, vous trouvez que
\(v_B^2 = 5gR\)
Prenons un exemple concret : si par exemple le rayon de la boucle est de 2 mètres, il faut une vitesse d’environ 10 mètres par secondes, soit 36 km/h. Raisonnable, non ? Pas si sûr…
Jusqu’ici, tout va bien
 Maintenant, calculons un peu la force à laquelle vous êtes soumis au moment où vous entrez dans la boucle. D’une part vous subissez votre poids; d’autre part, puisque vous vous engagez dans une trajectoire circulaire, vous subissez également une force centrifuge qui vous entraîne vers l’extérieur de la courbe, c’est-à-dire aussi vers le bas.
Maintenant, calculons un peu la force à laquelle vous êtes soumis au moment où vous entrez dans la boucle. D’une part vous subissez votre poids; d’autre part, puisque vous vous engagez dans une trajectoire circulaire, vous subissez également une force centrifuge qui vous entraîne vers l’extérieur de la courbe, c’est-à-dire aussi vers le bas.
A nouveau nous pouvons calculer la force centrifuge, qui vaut \(mv_B^2/R\), donc la force totale que l’on subit en bas de la boucle est
\(F_B = mg + mv_B^2/R\)
Or juste avant, nous venons précisément de calculer que \(v_B^2 = 5gR\), on a donc la force totale à l’entrée de la boucle
\(F_B = 6mg\).
Regardez bien cette expression, elle signifie que quand vous entrez dans la courbe du looping, vous subissez une force égale à 6 fois la force de pesanteur. Ce qu’on appelle communément une force de « 6g ». Et en principe, une force de 6g doit vous envoyer au tapis ! Alors, c’est comme ça qu’on meurt dans Destination Finale 3 ?
Comme vous le savez sans doute, ce sont les astronautes et les pilotes de chasse qui subissent le plus de « g », et sans entraînement ou équipement spécifique, ils s’évanouissent. Voyez par exemple la vidéo ci-dessous, qui montre un entraînement à 9g.
[youtube=http://www.youtube.com/watch?v=lK8U8RZyzsM]
Mais alors, comment survivre dans un looping ?
Pour en revenir à notre looping, si les pilotes de chasse s’évanouissent à 9g, comment peut-on supporter 6g ? La réponse est qu’on a pas vraiment à les supporter, car les designers de montagnes russes sont malins ! En effet le calcul que nous venons de faire est valable pour une boucle en forme de cercle, mais si on utilise une forme différente, on peut contourner le problème !
L’idée est d’utiliser une trajectoire dont le rayon de courbure soit grand en bas (pour éviter un trop grand choc), mais petit en haut, pour avoir une force centrifuge élevée qui nous scotche aux rails.
Ci-contre vous en voyez un exemple : on utilise typiquement une courbe que les mathématiciens appelle clothoïde, et dont le rayon de courbure augmente décroit au fur et à mesure que l’on avance dans la courbe. Puis au sommet, on inverse la clothoïde et le rayon de courbure augmente à nouveau.
Les clothoïdes sont également très appréciées pour les sorties d’autoroutes : puisque leur rayon de courbure augmente linéairement, on peut les emprunter en tournant le volant à vitesse constante.
Pour aller les plus loin
En réalité notre résistance à l’accélération ne dépend pas seulement du nombre de « g ». Elle dépend aussi de la durée pendant laquelle on les subit, et de la direction de l’accélération. En pratique on supporte bien mieux une accélération dirigée vers l’avant qu’une accélération dirigée vers le bas, qui nous envoie le sang dans la tête. C’est d’ailleurs le principe des combinaison anti-g des pilotes, qui permettent de maintenir le sang un peu en place, et donc de limiter les effets de l’accélération. Sur Wikipedia, on trouve les recommandations de la NASA, et d’après eux on peut tenir 3 minutes avec une accélération de 6g vers le bas. Comme quoi même sans clothoïde, votre prochain tour de montagnes russes ne devrait vraiment pas être votre destination finale…
PS : Sinon ce week-end, j’ai passé les 100 000 pages vues sur ce blog depuis sa création, merci à tous mes visiteurs !





31 Comments
Je te confirme que l’expression de la force centrifuge n’est plus enseignée au lycée. En classes préparatoires, cette formule n’est vue que lorsqu’on fait la dynamique du point en référentiel non galiléen.
Bref, c’est un joli article, comme toujours !
Enfer et damnation !
Alors démonstration en 2 lignes de la valeur de l’accélération centrifuge : on considère un mouvement circulaire de rayon R et de vitesse angulaire A, on l’écrit :
x(t) = R cos(At) et y(t) = R sin(At)
On dérive deux fois par rapport au temps, on trouve le vecteur accélération dont la norme vaut
A²R, et comme la vitesse linéaire est v=AR, on trouve bien v²/R.
Bigre !
Par chance, à mon époque (1996–1999), c’était encore enseigné (ah, les mobiles autoporteurs !), mais je ne sais plus en quelle année.
Quel est l’intelligent ministre qui a encore sabré dans les programmes scolaires ?
Sinon :
> une accélération dirigée vers le bas, qui nous envoie le sang dans la tête.
Une accélération vers le bas (dans le référentiel du corps, non dans le référentiel terrestre) ne devrait-elle pas au contraire vider la tête de son sang 😉 ?
Pingback: Sciences | Pearltrees
Belle article,
Petite correction, tu as écris:
« Ci-contre vous en voyez un exemple : on utilise typiquement une courbe que les mathématiciens appelle clothoïde, et dont le rayon de courbure augmente au fur et à mesure que l’on avance dans la courbe. »
Lorsque l’on avance sur la courbe, tel le chariot sur ces rails s’engageant dans le looping, le rayon de courbure diminue d’abord, trouve son minimum à l’apogée du looping puis augmente ensuite…
Bon weekend :))
Oula, oui tu as raison !!! Il faut que je corrige ça !
C’est très clair mais un truc me chiffonne :
Dans le cas où la boucle du looping est un cercle parfait, entre le moment qui précède immédiatement l’entrée dans le looping, et le moment qui le suit immédiatement, il semblerait que le corps passe par une forte discontinuité dans les forces subies: de mg à 5mg alors que finalement, il n’a fait qu’attaquer la courbe par une tangente…
Ça semble étrange ou pour le moins contre intuitif ne trouvez-vous pas ?
Effectivement, c’est contre-intuitif ! Je n’y avais pas vraiment réfléchi !
Mais je ne pense pas que ce soit forcément problématique. Si c’est correct, on a une discontinuité dans l’accéleration, ou bien un « jerk » infini (les anglos saxons utilisent ce terme pour la derivée de l’accéleration). Bon évidemment tout cela est théorique puisque les courbes ne sont jamais parfaites, mais je pense que meme sur le plan theorique cette singularité n’est pas un souci.
« L’idée est d’utiliser une trajectoire dont le rayon de courbure soit grand en bas (pour éviter un trop grand choc), mais petit en haut, pour avoir une force centrifuge élevée qui nous scotche aux rails. »
Dans ce cas lorsque l’on rentre dans un looping, le choc est moindre comparé à une boucle parfaite, mais du coup les formules précédentes sont plus où moins réfutées, non? (je suis en première et mon TPE est sur les montagnes russes)
En fait non c’est bon je viens de comprendre que ça ne change pas grand chose sauf le poids des passagers, désolée 🙂
Pingback: Peut-on se faire piéger par un feu rouge ? | Science étonnante
Bonjour, dans la partie « Deuxième condition : arriver jusqu’en haut », je ne comprends pas comment vous trouvez Vb²=5gR… ne serait-ce pas 4gR ?
D’ailleurs dans un de mes contrôles de L1, on nous donnait carrément Vb=racine(gR)… à retrouver ! Je n’ai jamais compris comment ils ont pu trouver cette formule ! ^^
Désolé, j’ai compris pourquoi le 5gR, il suffisait d elir ela phrase d’après un peu plus attentivement ! ^^
Pingback: Jusqu’où ira le record du saut à la perche ? | Science étonnante
Pingback: Crise énergétique ? Mais non, crise entropique ! | Science étonnante
Pingback: Crise énergétique ? Mais non, crise entropique !
Dans tes calculs tu négliges les frottements (ce qui est compréhensible pour le but visé ici), mais on néglige tout le temps les frottements, et personnellement je trouve ça frustrant. Même si ils font intervenir des coefficients indémontrables pour monsieur tout le monde, je pense que cela serait intéressant de faire un billet sur les différents frottements et une méthode simplifiée pour les calculer, l’histoire d’améliorer un peu nos calculs de table.
Beau travail sinon, j’ai toujours un immense plaisir à vous lire
Bien cordialement
Eric
Aïe, j’ai mal à ma physique, très mal, de voir que vous avez confondu la force centrifuge et la force centripète. En effet, c’est la deuxième qui correspond avec ce dont vous discutiez dans l’article, et non la première! Un petit passage sur Wikipédia vous permettra de clarifier ces notions dans votre esprit (ces deux forces sont très différentes dans leur nature, et elles ne doivent en aucun cas être confondues).
Même si cet article se voulait léger et amusant, j’espère que vous serez en mesure de corriger cette erreur afin de ne pas désinformer ceux qui étudieront ce sujet dans les années à venir!
Euh je ne suis pas sûr de voir ce que vous voulez dire !
A quel endroit exactement ?
A priori, la clothoïde, bien que meilleure que le cercle n’est pas la courbe optimale. La clothoïde est la courbe qui permet d’avoir une augmentation linéaire du rayon de courbure. Pratique pour une bretelle d’autoroute ou un virage, où le conducteur devra donc tourner le volant avec une vitesse régulière.
Pour un looping de grand huit, la quintique de l’Hospital est encore mieux car c’est la courbe à réaction constante (et donc à force constante exercée sur les passagers).
Deux liens qui en parlent (plus ou moins brièvement):
http://colin.pitrat.free.fr/?p=354
http://www.mathcurve.com/courbes2d/quintique%20de%20l’hospital/quintique%20de%20l’hospital.shtml
D’un autre côté, c’est purement théorique, dans les grand huit on ne recherche pas vraiment le confort des passagers (mais on se soucie quand même de leur survie !).
Bonjour.
Je fais un Tpe sur les loopings. Votre article est donc une source précieuse d’informations pour nous.
Cependant, je n’arrive pas à comprendre pourquoi la réaction des rails sur le wagon est négligée.
Merci.
Bonjour,
Non elle n’est pas négligée du tout ! J’ai juste omis de la représenter sur mes schémas (c’est un tort !). C’est simple, elle vaut toujours l’opposé de la somme « poids+force centrifuge ».
Bonjour, je fais actuellement un TIPE sur ce sujet, étant en deuxième année de prépa je cherche à comprendre précisément votre démarche. Pourriez vous expliciter vos calculs, notamment votre choix de référentiel (galiléen ou non, pour l’utilisation de la force centrifuge) et de coordonnées ?
Bonjour, est ce que ces calculs sont adaptables a un looping ovale ? si oui comment ?
Merci
Pingback: Crise énergétique ? Mais non, crise entropique ! - Adrastia
Pingback: Espacetpe | Pearltrees
Je suis en Daeu b (diplôme d accès aux études universitaires scientifiques) je n évolue ques dans des repère terrestre dit galiléen mon prof dit que la force centrifuge n existe pas comment la traduire dans le PFD . il suffit de rajouter une force ??? Il en est de même avec les énergies ??
blc frr
ta trop raison frr
Bonjour d’un de vos ancien profs (math sup… cela fait longtemps) Bravo pour ce petit cours de physique simple et bien écrit. Il n’y a plus de géométrie nulle part dans les programmes de prépa donc plus d’étude des arcs…
Merci pour le commentaire ! C’est un plaisir de vous retrouver après toutes ces années ! Je vous ai envoyé un email, j’espère qu’il vous parviendra