Pour réaliser le moteur électrique le plus simple du monde, vous n’avez besoin que de 4 composants : une pile, un aimant, un fil de cuivre et une vis. Voyons un peu cette expérience très simple, et la physique qui est derrière. L’occasion peut être pour vous de (re-)découvrir le principe du moteur électrique !
De l’expérience avant toute chose
Pour réaliser cette expérience, procurez vous une vis, une pile AA de 1.5 volt, un fil de cuivre et un aimant. Placez l’aimant sur la tête de la vis, laquelle doit ainsi se magnétiser, et pouvoir tenir aimantée sur un des pôles de la pile. Connectez une des extrémités du fil de cuivre sur l’aimant et la seconde sur le pôle opposé de la pile.
Et voilà le résultat, l’aimant et la vis se mettent en rotation ! Comme vous pouvez le voir je n’ai pas chômé cette fois, puisque j’ai vraiment fait l’expérience moi-même !
[youtube= »http://www.youtube.com/watch?v=SMsIPxFWGRo »]
(les plus observateurs auront remarqué que j’ai même essayé de faire la synthèse additive des couleurs en même temps !)
Attention car après quelques secondes le fil de cuivre s’échauffe beaucoup par effet Joule. C’est normal car dans ce montage on fait un court-circuit de la pile ! D’ailleurs toute cette énergie perdue inutilement en chaleur traduit le rendement assez mauvais de ce type de moteur.
Pour que cela fonctionne chez vous, il vous faudra peut être jouer un peu avec le type de vis, et le poids de l’ensemble pour minimiser le frottement entre la pointe de la vis et la pile. Mais pour que la manip marche bien, la principe subtilité matérielle c’est de trouver un aimant suffisamment puissant. Pour ma part j’ai utilisé un aimant dit « néodyme ».
Les aimants au néodyme
Le néodyme est un métal blanc qui est le 60ème élément de la classification périodique. Il appartient au groupe des terres rares. En 1982, des chercheurs de General Electric découvrent qu’un alliage de néodyme, de fer et de bore conduit à un matériau puissamment aimanté.
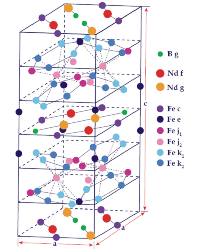
Il s’avère que cet alliage permet de créer un composé bien particulier, de formule chimique Nd2Fe14B, et possédant une structure cristalline très anisotrope qui favorise l’apparition d’une aimantation spontanée très directionnelle (voir ci-contre la structure plutôt alambiquée du composé [1])
Cet alliage permet ainsi de réaliser des aimants permanents qui sont typiquement 10 fois plus puissants que les aimants classiques en ferrite. Ces aimants au néodyme sont à ce jour utilisés dans de nombreuses applications industrielles comme les disques durs, les haut-parleurs ou les écouteurs.
Mais pourquoi est-ce que çà tourne ? Demandez donc à Lorentz !
Pour comprendre ce qui se passe dans notre montage, il faut savoir que la surface des aimants néodymes est généralement recouverte de chrome. Donc le courant électrique circule à la surface de l’aimant. Les électrons qui forment ce courant baignent alors totalement dans le champ magnétique créé par l’aimant.
J’espère que c’est quelque chose que l’on apprend toujours au lycée, mais quand une particule chargée (comme des électrons) se déplace dans un champ magnétique, elle subit une force appelée force de Lorentz, qui s’exprime comme ceci :
\(\vec{F} = q \vec{v} \times \vec{B}\)
où q est la charge de la particule, v sa vitesse et B le champ magnétique. Le symbole \(\times\) désigne le produit vectoriel, vous savez le truc que l’on fait avec les trois doigts de la main droite pour connaître l’orientation du vecteur résultant.
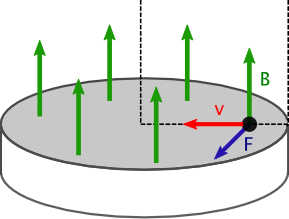Donc mettez vous à la place d’un petit électron (la boule noire sur mon schéma ci-contre) : vous voyagez à la surface de l’aimant sous l’impulsion de la tension de la pile. Mais vous êtes dans le champ magnétique et vous subissez en plus la force de Lorentz. Celle-ci (en bleu sur mon schéma) est dans le plan de la surface de l’aimant, perpendiculaire à la direction de déplacement du courant. Et c’est cette force qui met le disque en rotation !
D’ailleurs on peut se demander pourquoi la force de Lorentz entraîne l’ensemble du disque, et pas seulement les électrons qui la subissent ? Ne pourrait-il pas y avoir un courant de surface constitué d’électrons qui spiralent, tout en laissant l’aimant immobile ? Je n’ai pas la réponse à cette question !
Un moteur connu depuis longtemps
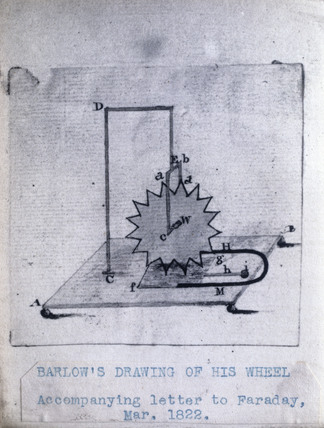Ce type de moteur a été imaginé par Mickael Faraday en 1821. Une variante proche en est la fameuse roue inventée en 1822 par le physicien britannique Peter Barlow. Le montage en est différent mais le principe analogue. Il est décrit sur le dessin ci-contre, extrait d’une lettre adressée par Barlow à Faraday.
Une roue dentée trempe dans un bain de mercure, lui-même placé dans un champ magnétique. Une pile est alors reliée à la roue et au bain de mercure, qui est conducteur. Les électrons voyagent dans les pointes de la roue, et subissent la force de Lorentz sous l’effet du champ magnétique, et la roue tourne !
Pour les curieux, le même principe est également à la base de la magnéto-hydro-dynamique. On fait circuler un courant entre deux électrodes accrochées à un bateau, et plongées dans l’eau de mer.
Si on ajoute un gros aimant au dispositif, les ions chargés présents dans l’eau de mer (et qui transportent le courant électrique) subissent la force de Lorentz : l’eau salée est entraînée sous le bateau…et donc le bateau avance !
Là aussi le rendement est assez pauvre, mais l’idée très jolie ! C’est elle qui a inspiré Tom Clancy, l’auteur de ‘A la poursuite d’Octobre Rouge’, pour imaginer son révolutionnaire sous-marin russe furtif.
Encore plus fort
En fait je vous ai menti. Le moteur à 4 pièces n’est pas le moteur le plus simple du monde. On peut se débarrasser de la vis et faire encore mieux. Cette fois l’aimant est fixe, et c’est le fil lui-même qui tourne !
Admirez !
[youtube= »http://www.youtube.com/watch?v=zOdboRYf1hM »]
PS : et pitié pas de commentaires de génies méconnus ayant mis au point des inventions qui permettent de produire de l’énergie infinie et gratuite avec des aimants qui bougent, tout en violant le premier principe de la thermodynamique (qui bien sûr n’est pas consentant).
PS2 : pour alimenter le débat sur ce qui fait que les électrons entraînent l’ensemble du disque, on peut calculer l’ordre de grandeur de la force de Lorentz, rapporté à la force électrique que les électrons subissent du fait de la tension de la pile. Celle-ci vaut qE et la force de Lorentz qvB. Or la vitesse v est reliée au champ électrique E par la mobilité mu, avec v = mu.E. Donc le ratio de la force de Lorentz sur la force électrique est égal q.mu.E.B / qE = mu.B. Pour les électrons dans du cuivre, la mobilité mu vaut quelques 10-3 (en unité SI, des kg-1.s2.A). Si mon aimant produit un champ de l’ordre du Tesla, ça nous fait quand même une force de Lorentz 1000 fois plus petite que celle qui entraîne les électrons !
PS3 : D’autres blogueurs ont bien sûr déjà évoqué le sujet (ici ou là)
[1] J. Herbst et al, Relationships Between Crystal Structure and Magnetic Properties in Nd2Fe14B, Physical Review B, 29 (1984) , dispo ici
13 Comments
Excellent !!!
Si ça peut aider, la force subie par les électrons se transmet à l’ensemble du matériau si celui-ci est mobile. Si il est fixe, la force de Lorentz se manifeste par l’effet Hall, c’est à dire une répartition de charge différente dans le matériau à cause du déplacement des électrons.
Oui j’ai bien pensé à ça, mais ça ne me satisfait pas pour la raison suivante : prenons un barreau métallique que l’on pose sur une surface sans frottements (par exemple sur de la glace ou un coussin d’air). Si on applique une tension aux extrémités de ce barreau, les électrons circulent dedans, mais n’entraînent pas le barreau pour autant !
Si le barreau est plongé dans un champ magnétique de direction adaptée, il me semble que si. De la même manière, si on pose un cylindre métallique sur deux rails entre lesquels on applique une différence de potentielle et qu’on met un aimant, le cylindre se met à rouler.
Ah pardon, je me suis mal exprimé. Je ne parlais pas d’une force de Lorentz mais de la force électrostatique qui existe dans le barreau sous l’effet du champ électrique créé par la tension d’une pile. D’après mon calcul d’ordre de grandeur, cette force électrostatique est 1000 fois plus intense que ce qu’on a avec une force de Lorentz, et cette force électrostatique déplace les électrons dans le barreau, sans que ces derniers entrainent l’ensemble du barreau.
C’est très naïf, mais est-ce que si l’aimant était posé en dessous au lieu de tourner avec le moteur, ça marcherait ?
Bon, et autre question : puisque ça tourne, les noyaux, chargés positivement, subissent une force de Lorentz eux-aussi ! Non ?!
Le système « barreau » étant isolé, tout déplacement de matière à l’imterieur du barreau n’entraînera pas de modification dans le mouvement de son centre d’inertie! Tout comme des cosmonautes se déplaçant dans la station orbitale et ne modifiant pas son mouvement
Bonjour,
Excellente question.
Je pense qu’en effet, ton calcul est exact : les électrons subissent une force très importante de la part de E (1000 fois celle due à B), et que cette force est en réalité bien transmise intégralement au métal.
Mais : les ions du réseau cristallin subissent une force exactement opposée, qui fait que la résultante totale sur le métal s’annule, et il ne bouge pas.
C’est différent pour la force due à B évidemment, puisqu’elle est en v^B, et les ions immobiles ne la ressentent pas.
Cela répond donc aussi à l’interrogation du texte principal « pourquoi l’aimant est entrainé, pourquoi pas un système de courants circulaires ? » : c’est bien parce que toute force subie par les électrons est transmise au métal (via les collisions avec le réseau cristallin). Donc les électrons ne peuvent pas se promener librement et l’aimant est entrainé.
Est-ce qu’en minimisant l’effet Joule, par exemple en utilisant des matériaux supraconducteurs, on pourrait augmenter considérable le rendement, ou au contraire, est-ce que les forces de frottements sont nécessaires au mouvement, un peu comme en mécanique ?
Ben en théorie ça ne marche pas avec un supraconducteur : ces derniers ont la propriété d’ejecter les lignes de champ magnétique, le fameux effet Meissner. Donc le champ ne pourra pas pénétrer dans le supraconducteur et les électrons ne le verront pas !
c’est en mettant une bobine que le rendement s’améliore, car si on met un supraconducteur c’est la pile qui va chauffer avec la résistance interne
Pingback: Pause estivale, avenir transatlantique et loi de Zipf « Science étonnante
Pingback: Ralentir le temps // Aimant au néodyme et cuivre // Etranges Objets