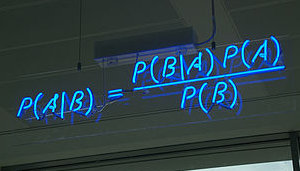Préliminaire : Ce billet est la suite de celui de la semaine dernière, qui portait sur les probabilités conditionnelles et introduisait la formule de Bayes. Si ces notions vous sont familières, vous n’êtes pas obligés d’aller le lire. Dans le cas contraire, n’hésitez pas à vous rafraîchir la mémoire !
 La semaine dernière, je vous ai présenté la célèbre règle de Bayes, qui permet de relier la probabilité conditionnelle de « A sachant B » à celle de « B sachant A »
La semaine dernière, je vous ai présenté la célèbre règle de Bayes, qui permet de relier la probabilité conditionnelle de « A sachant B » à celle de « B sachant A »
$latex P(A | B) = \frac{P(B | A) P(A)}{P(B)}&s=2&fg=0000ff$
Nous avions vu un cas simple, où A et B désignaient respectivement le fait d’être rouge et carré pour un objet que l’on tire au hasard dans une urne (« quelle est la probabilité qu’il soit carré sachant qu’il est rouge »), ainsi qu’un cas plus subtil où il était question de dépistage du cancer.
L’idée était de souligner la différence entre « la probabilité d’avoir le cancer sachant qu’on est dépisté positif », notée P(C | +), et « la probabilité d’être dépisté positif sachant qu’on a le cancer », notée P(+ | C). D’après la formule de Bayes, on peut relier les deux par :
$latex P(C | +) = \frac{P(+ | C) P(C)}{P(+)}$
Aujourd’hui, nous allons voir en quoi la formule de Bayes peut s’interpréter dans un contexte plus général, et devenir un outil formidable pour quantifier la manière dont nous raisonnons, et même dont notre cerveau fonctionne !
 Non, le paradoxe de Simpson ne tire pas son nom de Homer, mais de Edward Simpson, le statisticien qui l’a décrit pour la première fois en 1951. Il s’agit d’un de ces paradoxes mathématiques qui peut nous faire des noeuds à la tête, mais qui malheureusement est bien plus qu’une simple curiosité : bien comprendre ce paradoxe peut s’avérer essentiel pour prendre les bonnes décisions !
Non, le paradoxe de Simpson ne tire pas son nom de Homer, mais de Edward Simpson, le statisticien qui l’a décrit pour la première fois en 1951. Il s’agit d’un de ces paradoxes mathématiques qui peut nous faire des noeuds à la tête, mais qui malheureusement est bien plus qu’une simple curiosité : bien comprendre ce paradoxe peut s’avérer essentiel pour prendre les bonnes décisions !

 C’est en cours de philo que j’en ai entendu parler pour la première fois ! Notre prof nous faisait un cours sur la logique et ses fondements, et c’est alors qu’elle le mentionna : le fameux théorème de Gödel, celui qui prouve que quoi qu’on fasse, il existe des énoncés mathématiques vrais, mais indémontrables. Les mathématiques resteront à tout jamais un édifice imparfait !
C’est en cours de philo que j’en ai entendu parler pour la première fois ! Notre prof nous faisait un cours sur la logique et ses fondements, et c’est alors qu’elle le mentionna : le fameux théorème de Gödel, celui qui prouve que quoi qu’on fasse, il existe des énoncés mathématiques vrais, mais indémontrables. Les mathématiques resteront à tout jamais un édifice imparfait !