Le sujet du jour est un grand classique, l’une des découvertes majeures du XXe siècle : la théorie du chaos.
On pourrait écrire tout un bouquin sur le sujet — et d’ailleurs il y en a, cf J.Gleick ou I.Stewart — alors je ne vais pas chercher dans ce billet à compléter tout ce que je n’ai pas dit dans la vidéo, mais au moins à pointer vers quelques pistes ou résultats intéressants.
Edit : tous les codes Python des simulations sont là : https://github.com/scienceetonnante/Chaos
L’étude des systèmes dynamiques
Commençons par un peu de formalisme pour bien poser le cadre mathématique dans lequel on étudie les systèmes dynamiques dont on a parlé. Nous en avons vu deux types dans la vidéo : les systèmes en temps continu (pendule, planètes, équations de Lorenz…) et les systèmes en temps discret (transformation logistique, de Hénon…).
Pour les systèmes en temps discret, le jeu est relativement simple. On a des variables qui décrivent l’état du système. Et pour passer au pas de temps suivant, on applique une transformation qui agit sur ces variables.
Pour les systèmes en temps continu, c’est plus subtil. Imaginons que l’on ait un certain nombre N de variables numériques décrivant l’état de notre système à un instant donné : \(x_1, x_2, x_3…x_N\). On peut regrouper toutes ces variables en un vecteur \(\vec{X}\) de dimension N (dans la suite, je vais laisser tomber les flèches).
L’espace des états possible (l’espace dans lequel X prend ses valeurs) est appelé espace des phases. On reviendra sur ce terme. Pour schématiser on va dire que l’espace des phases est \(\mathbb{R}^N\), mais on peut très bien avoir des variables qui varient sur un domaine plus restreint.
On considère pour X une équation d’évolution de la forme
\(\frac{dX}{dt} = F(X(t))\)
Ceci est une équation différentielle du 1er ordre, et dans cette expression F est une fonction de \(\mathbb{R}^N\) vers \(\mathbb{R}^N\).
Toute l’évolution du système est contenue dans cette fonction F. Si on sait calculer F, on peut simuler numériquement l’évolution du système en choisissant un intervalle de temps très petit \(\Delta t\), et en calculant l’évolution \(\Delta X\) des variables X par
\(\Delta X = F(X) \Delta t\).
C’est comme ça que j’ai fait toutes les simulations du système de Lorenz (et que lui avait fait à l’époque sur son LGP-30 !)
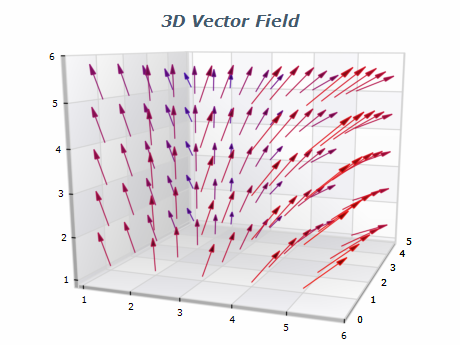
Autre représentation alternative de F, la voir comme un champ de vecteurs. F nous donne l’évolution de X en renvoyant un vecteur en chaque point de l’espace des phases. Et donc l’intégralité de l’information contenue dans F peut se retrouver dans une représentation graphique sous forme d’un champ de vecteur sur l’espace des phases, un truc du genre :
Pour calculer une trajectoire à partir d’un point de l’espace des phases dans ce champ de vecteur, c’est en principe très simple : on suit les flèches ! « Suivre les flèches » est la version graphique de la méthode de calcul que j’ai présentée ci-dessus, où on fait une simulation par petits intervalles de temps discret. On dit dans les deux cas qu’on intègre la trajectoire.
Une précision importante : j’ai parlé dans ma vidéo de systèmes qui ne sont pas a priori régis par une équation d’évolution du 1er ordre, mais du 2nd ordre. C’est le cas des systèmes mécaniques en général, par exemple le pendule simple
\(\frac{d^2\theta}{dt^2}=-\frac{g}{L}\sin\theta\)
Dans ce cas il y a une façon simple d’en faire un système du premier ordre : dédoubler les variables. Pour décrire l’état complet du pendule, et prédire son évolution, son angle \(\theta\) ne suffit pas, il nous faut aussi sa vitesse angulaire \(\omega\), qui bien sûr est égale à la dérivée de l’angle.
On peut donc remplacer l’équation du second ordre par les deux équations du premier ordre
\(\frac{d\omega}{dt}=-\frac{g}{L}\sin\theta\)
\(\frac{d\theta}{dt}=\omega\)
On regroupe donc les 2 variables dans un vecteur, et on est bons. Pour le pendule simple, l’espace des phases est donc à 2 dimensions, et pour le pendule double, à 4 dimensions. On voit donc que l’espace des phases du système de Lorenz est d’une dimension inférieure à celui du double pendule. D’un certain point de vue, on peut dire que le système de Lorenz est un des plus « petits » systèmes continus chaotiques possibles.
D’ailleurs c’est l’occasion de revenir sur une affirmation de la vidéo qui vous a peut-être choquée : mathématiquement, deux orbites ne peuvent jamais se croiser. Ici, on parle bien d’orbites dans l’espace des phases ! Prenons le cas d’une planète dans un champ gravitationnel : il faut 3 nombres pour décrire sa position (x,y,z), mais comme l’équation du mouvement est du second ordre, il faut 6 nombres pour l’espace des phases : aux 3 positions on doit ajouter les 3 vitesses (ou les 3 impulsions).
Les orbites de deux planètes peuvent très bien se croiser en un même point de l’espace, mais pas de l’espace des phases ! Ce sont bien les orbites de l’espace des phases qui ne peuvent pas se croiser.
Une façon simple de le voir : vu que l’évolution d’un point est entièrement déterminée par sa position dans l’espace des phases (en suivant le champ de vecteur), si deux trajectoires se rencontrent, elles doivent forcément suivre la même évolution par la suite (et c’est cette observation qui a donné à Lorenz l’intuition que son attracteur ne pouvait pas avoir une structure simple).
Le modèle de Lorenz
Tout d’abord, laissez moi mentionner l’article fondateur de Lorenz que je n’ai pas cité explicitement. Je vous le recommande car il est d’une rare profondeur. C’est incroyable qu’il soit passé inaperçu des mathématiciens pendant près de 10 ans.
Lorenz, E. N. (1963). Deterministic nonperiodic flow. Journal of the atmospheric sciences, 20(2), 130-141.
(Au fait, je ne l’ai pas précisé, mais ce Lorenz est évidemment différent du LorenTz de la relativité !) Pour les fans de mécanique des fluides, on peut dire un tout petit mot du système de Lorenz, que j’ai présenté dans une forme qui semble ne pas avoir grand chose à voir avec l’atmosphère.
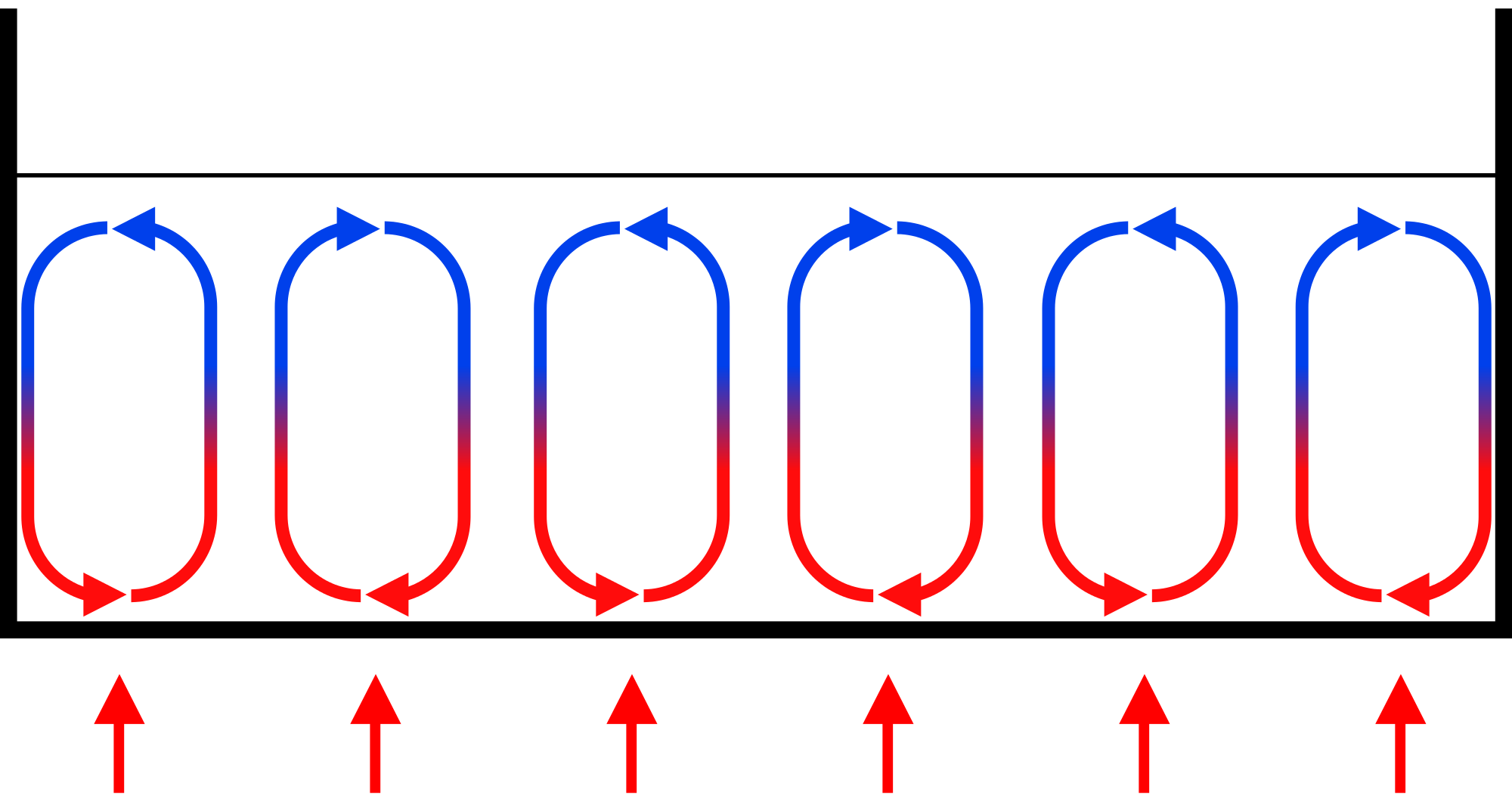
Pour l’origine de l’équation, on peut en gros s’imaginer qu’on part d’un modèle complet d’une couche de fluide soumis à la gravité et à un gradient de température : chaud en bas, froid en haut. Le mouvement de convection correspond à l’élévation du fluide chaud, son refroidissement, puis sa redescente.
Il s’agit donc d’un modèle très simplifié de convection sous l’effet d’un gradient de température, comme on en a à l’intérieur de la terre, dans l’atmosphère, dans une casserole ou dans ces lampes bizarres.
Le modèle de Lorenz s’obtient grossièrement à partir d’une équation initiale, qu’on va simplifier en ne gardant que les modes principaux. Et si on tronque à l’extrême, on se retrouve avec seulement 3 variables.
Dans le système d’équations, la variable x représente en gros l’intensité de la convection, la variable y le gradient de température, et la variable z la « non-linéarité » du gradient, c’est-à-dire à quel point le gradient dans l’épaisseur s’éloigne d’un truc gentiment linéaire.
Le système d’équation possède 3 paramètres, j’ai repris les valeurs numériques classiques qui figuraient dans l’article de Lorenz. \(\rho\) est en gros le nombre de Rayleigh, et on le prend suffisamment élevé pour que la convection se déclenche. Le paramètre \(\sigma\) est assimilable au nombre de Prandtl.
Quand peut-on dire d’un système qu’il est chaotique ?
Il n’y a pas de définition absolument unifiée de ce qui définit un système chaotique. Dans la vidéo, j’ai essentiellement suggéré qu’il s’agissait d’un système soumis à l’effet papillon…Dans la première version de la vidéo, j’ai aussi brièvement mentionné l’histoire du mélange des trajectoires, mais je l’ai finalement coupée dans le montage final, alors on va préciser.
Pour qualifier et quantifier l’effet papillon, on utilise une définition mathématiquement plus précise : on a un système chaotique si deux points très proches initialement divergent dans le temps avec une trajectoire exponentielle. Prenons deux points \(x_A\) et \(x_B\) séparés initialement par une distance \(\Delta x(0)\) faible. Si au bout d’un temps t on a
\(\Delta x(t) \sim \Delta x(0) exp(\gamma t)\)
c’est que les deux trajectoires divergent avec un écart qui croit exponentiellement avec le temps (évidemment on regarde ça pour les temps pas trop long, puisque dans un système de Lorenz les trajectoires sont bornées, donc ça ne diverge pas exponentiellement jusqu’à la St-Glinglin…)
Le coefficient \(\gamma\) décrit l’intensité de la divergence, et on l’appelle l’exposant de Lyapunov. Physiquement, il est homogène à l’inverse d’un temps, donc on peut le mettre sous une autre forme en écrivant \(\gamma = 1/\tau\) et avoir une divergence en \(e^{t/\tau}\). Dans ce cas on appelle \(\tau\) le temps de Lyapunov, et il correspond en gros au temps au bout duquel deux trajectoires initialement proches auront bien divergé. Pour faire simple, cela est lié au temps au bout duquel on a du mal à prédire l’évolution du système (par exemple quand on dit 2-3 semaines pour la météo).
Mais pour bien qualifier un système chaotique, cette divergence exponentielle ne suffit pas. Pour preuve, considérez le système suivant
\(\frac{dx}{dt} = x(t)\)
dont on connait évidemment la solution explicite :
\(x(t) = e^t\)
Vous pouvez vous convaincre que par construction, deux points initialement très proches vont diverger de façon exponentielle…et pourtant on peut difficilement le qualifier de système chaotique ! Pour faire la discrimination avec les « vrais » systèmes chaotiques, on peut ajouter une condition supplémentaire : celle du mélange des trajectoires. Clairement un système comme celui-là ne mélange pas les trajectoires.
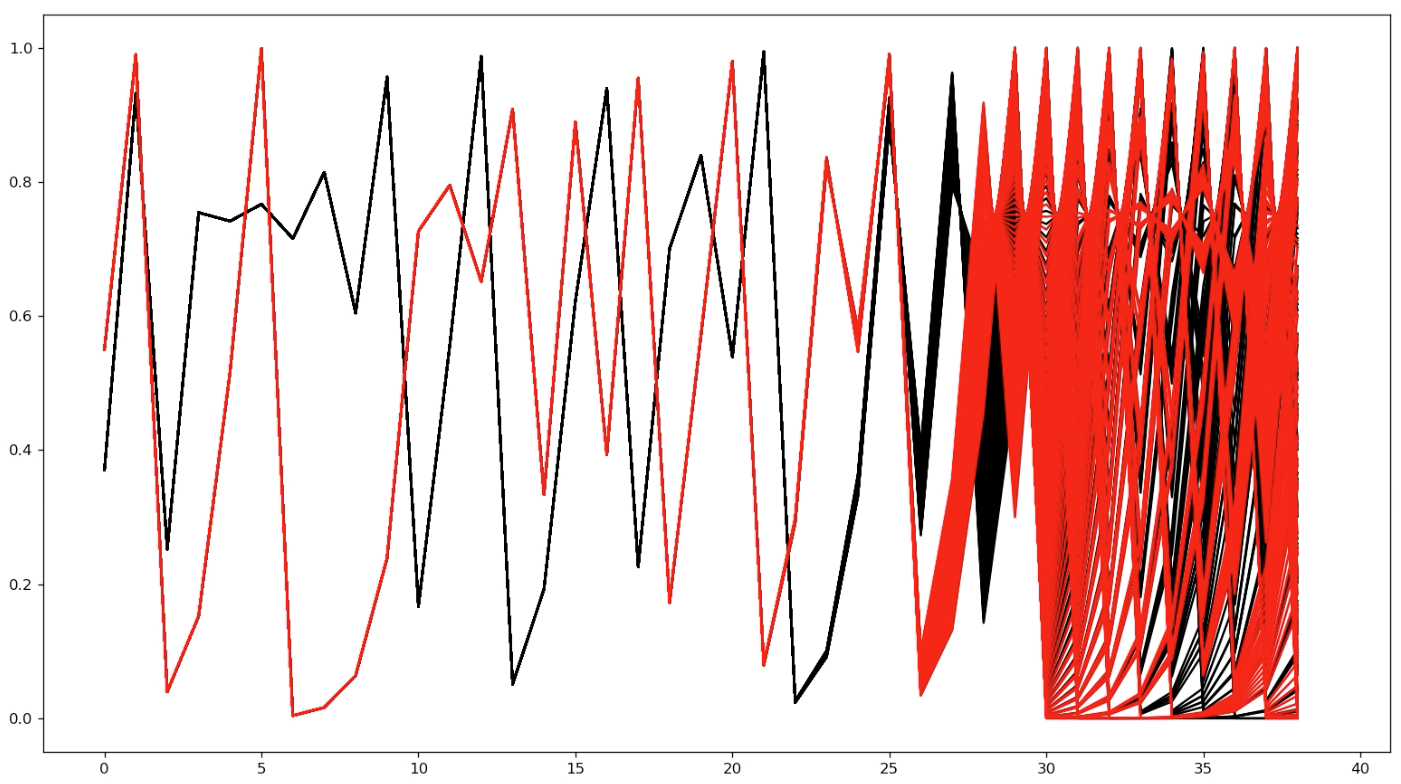
Dans la version initiale de la vidéo j’avais présenté la petite simulation suivante : on prend plein de points dans l’intervalle \(0.37 \pm 10^{-9}\) (courbe en noir), et plein de points dans l’intervalle \(0.55 \pm 10^{-9}\). Si on applique successivement la fonction logistique à tous ces points, les trajectoires rouges et noires finissent par diverger et se mélanger.
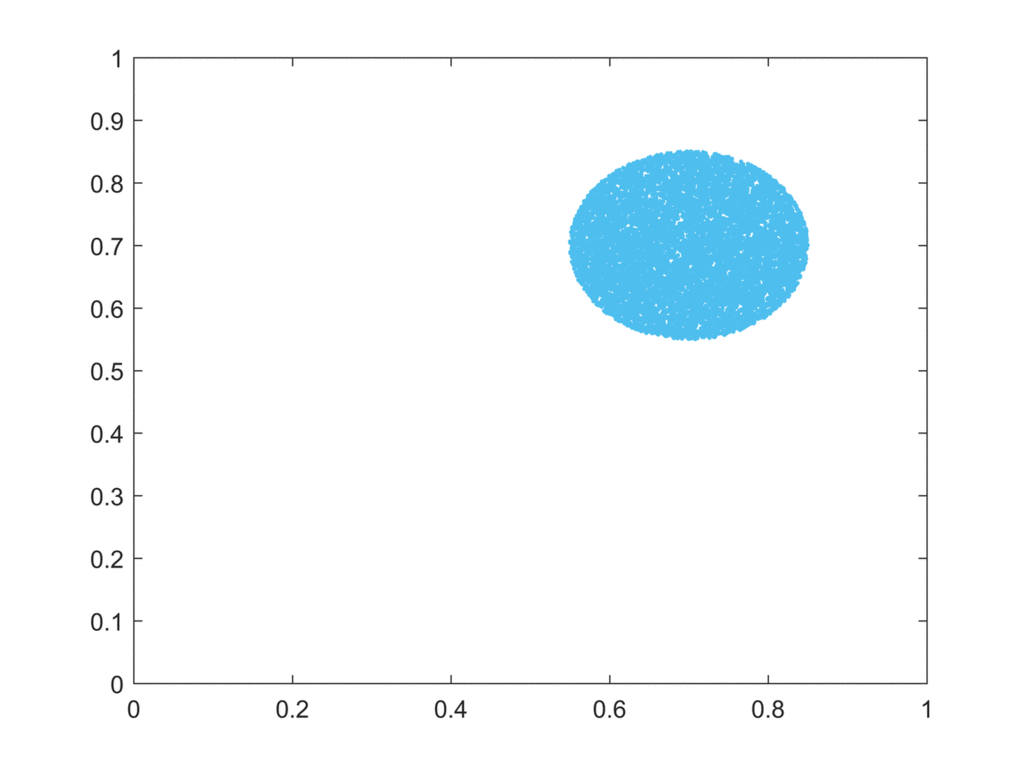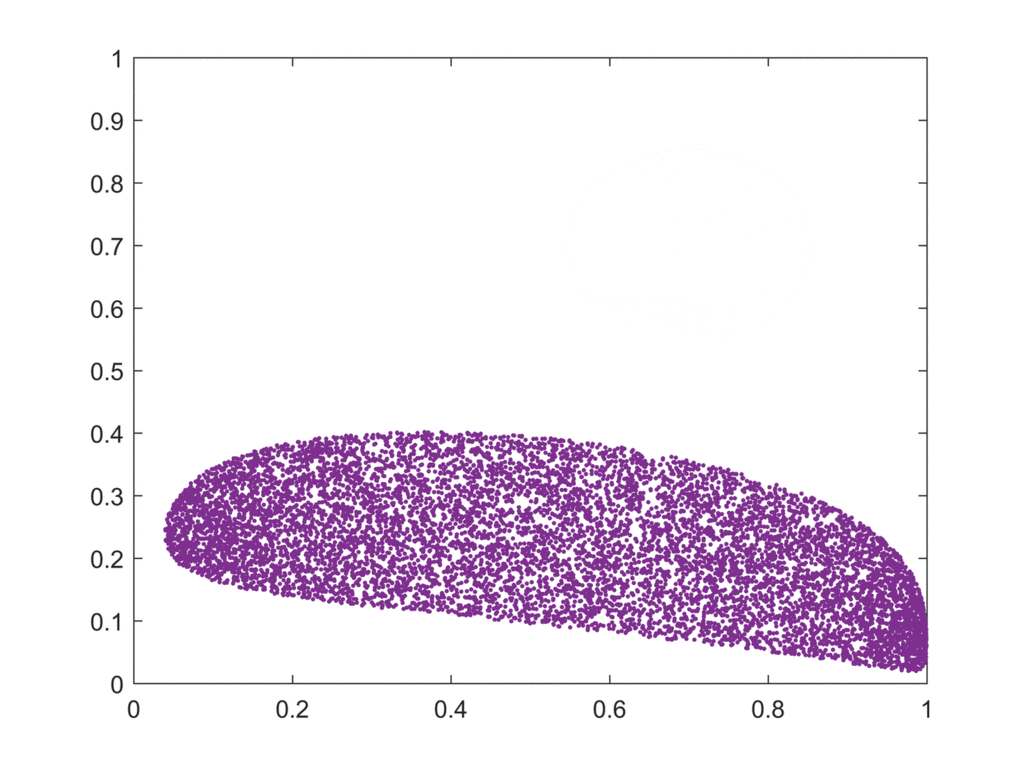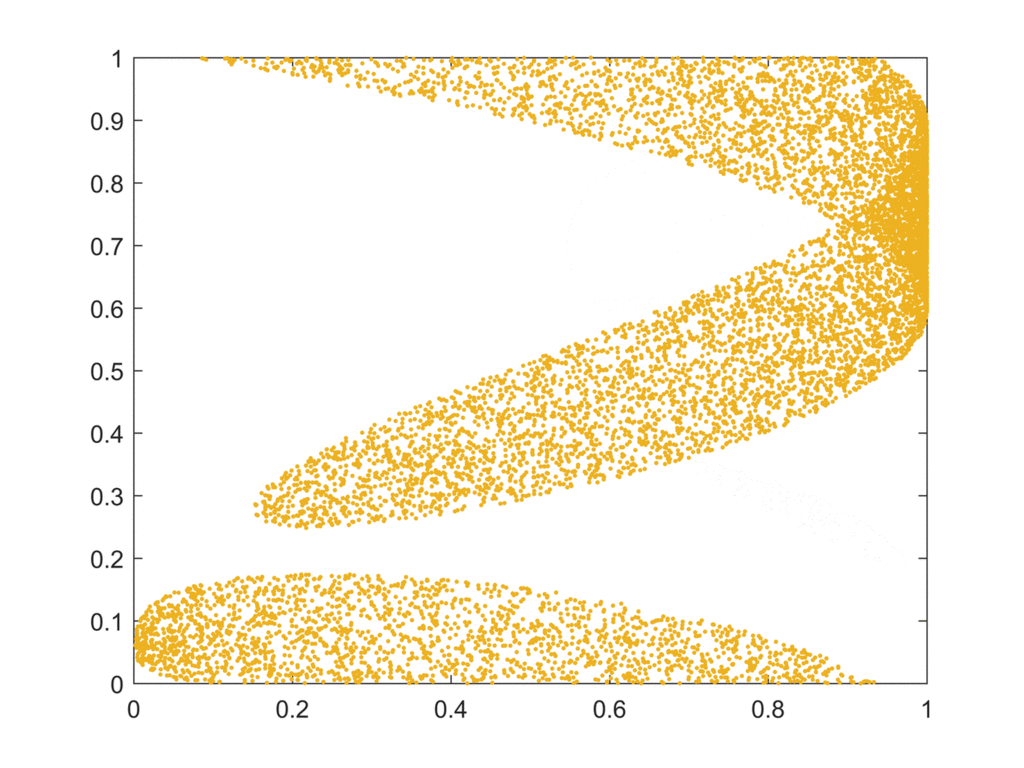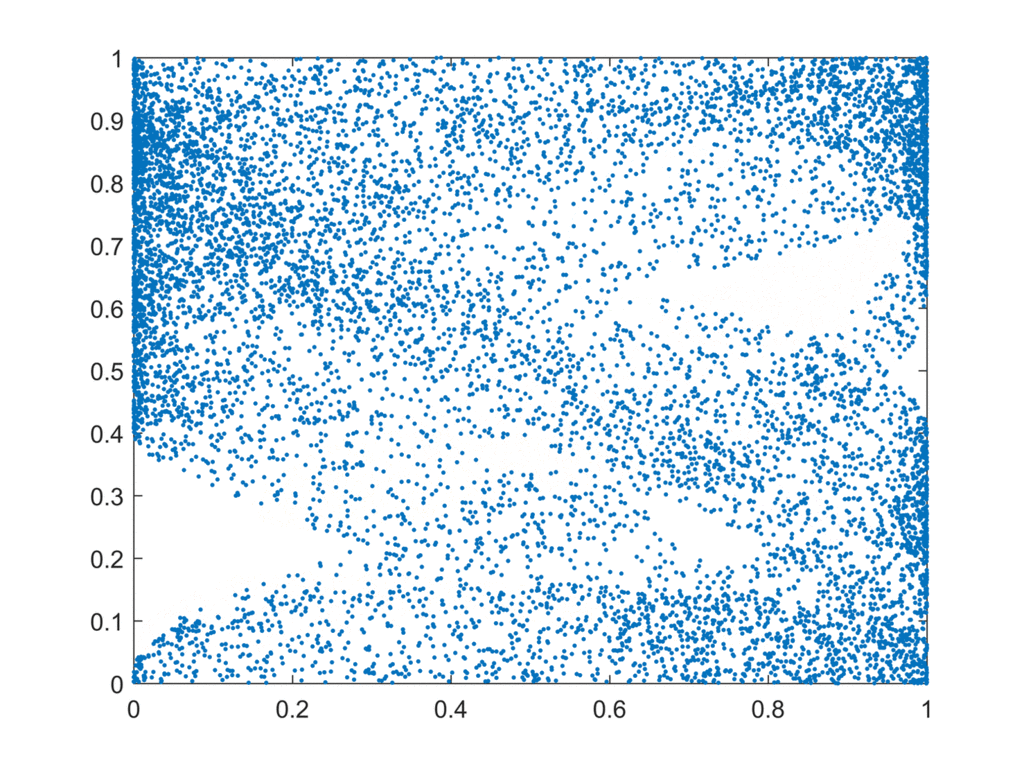
Mathématiquement, dans un système chaotique, si on prend deux petits intervalles ouverts quelconques, aussi petits qu’on veut, et qu’on simule leur évolution, au bout d’un certain temps les trajectoires seront totalement mélangées. C’est une condition qu’on ajoute, outre l’effet papillon, pour les systèmes chaotiques.
C’est ce qu’illustre ce petit gif animé qui montre les itérations successives d’un système chaotique à partir d’un ensemble de départ.
 On trouve parfois une troisième condition : l’existence d’orbites périodiques denses. De façon remarquable, Lorenz avait déjà noté ça dans son article fondateur !
On trouve parfois une troisième condition : l’existence d’orbites périodiques denses. De façon remarquable, Lorenz avait déjà noté ça dans son article fondateur !
Systèmes continus vs systèmes discrets
En réalité les systèmes continus et les systèmes discrets ne sont pas comme deux mondes à part. On peut notamment les relier au moyen de ce qu’on appelle une section de Poincaré.
Avant de parler de cette idée, qu’il me soit permit de dire un mot de Poincaré, qui d’une certaine manière peut être considéré comme l’un des premiers découvreurs de l’effet papillon. En effet il avait noté avant tout le monde qu’un système de 3 corps en interactions pouvait conduire à des instabilités, des sensibilités aux conditions initiales, et devenait vite imprédictible
En particulier dans Science et Méthode, en 1908, il écrivait :
Une cause très petite, qui nous échappe, détermine un effet considérable que nous ne pouvons pas ne pas voir, et alors nous disons que cet effet est dû au hasard. Si nous connaissions exactement les lois de la nature et la situation de l’univers à l’instant initial, nous pourrions prédire exactement la situation de ce même univers à un instant ultérieur. Mais, lors même que les lois naturelles n’auraient plus de secret pour nous, nous ne pourrons connaître la situation initiale qu’approximativement. Si cela nous permet de prévoir la situation ultérieure avec la même approximation, c’est tout ce qu’il nous faut, nous disons que le phénomène a été prévu, qu’il est régi par des lois ; mais il n’en est pas toujours ainsi, il peut arriver que de petites différences dans les conditions initiales en engendrent de très grandes dans les phénomènes finaux ; une petite erreur sur les premières produirait une erreur énorme sur les derniers. La prédiction devient impossible et nous avons le phénomène fortuit.
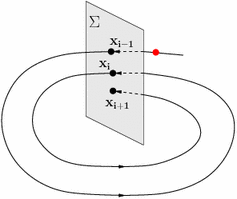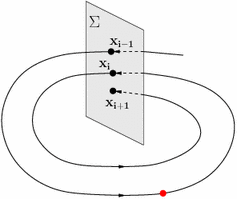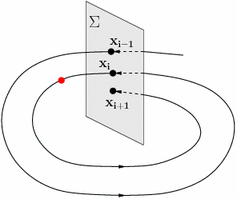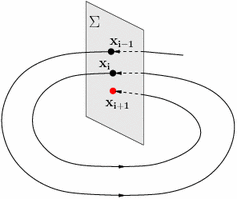
Revenons à la section de Poincaré. L’idée est assez simple : prenez un système continu en dimension D (pensez à celui de Lorenz, donc D=3) et considérez un hyperplan de l’espace des phases, de dimension D-1. Les trajectoires vont croiser de nombreuses fois ce plan, et on peut considérer les points d’intersection successifs au fur et à mesure que la trajectoire se prolonge. L’application qui a un point du plan associe le point suivant et une transformation en temps discret sur le plan.
La transformation de Hénon a, en fait, été initialement conçue par Michel Hénon comme une variante du système de Lorenz après section de Poincaré, dans le but de pouvoir révéler la structure fractale de l’attracteur de façon plus facile que le système de Lorenz.
Lorenz lui même avait déjà imaginé une astuce de ce genre. Il avait suggéré que les deux ailes de son attracteur semblaient se recoller au niveau d’un segment, et que toute trajectoire sembler passer par ce segment de façon périodique. On peut donc considérer l’application qui a un point du segment associe le point suivant sur la trajectoire. Lorenz avait montré que l’application en question ressemblait beaucoup à une fonction en forme de tente, qui exhibe un comportement chaotique du même genre que la fonction logistique.
D’ailleurs le caractère chaotique de la fonction logistique n’est pas du tout spécifique de cette fonction en particulier. Si on prend une fonction croissante puis décroissante de [0;1] dans lui-même, on peut obtenir le même genre de comportement, par exemple avec \(f(x) = \sin(\pi x)\).
Encore plus fort, ce qu’on a observé sur le diagramme de bifurcation de la fonction logistique est en fait assez générique. En particulier les écarts entre les points pour lesquels on observe un dédoublement.
Dans le cas de la fonction logistique, notons \(r_n\) le point de bifurcation au-delà duquel on a une orbite périodique constituée de \(2^n\) points, et ce jusqu’au point \(r_{n+1}\).
On a donc vu que \(r_1=3\), puis que \(r_2\approx 3.449\), et \(r_3\approx 3.544\). On a remarqué que les intervalles sont de plus en plus petits. En fait on peut montrer deux choses : d’une part que \(r_n\) tend vers \(\approx 3.56995…\), qui marque donc l’entrée dans le régime chaotique; et d’autre part que le ratio entre un intervalle et le suivant tend vers une constante, \(C\approx 4.66920\), appelée constante de Feigenbaum.
Ce qui est extraordinaire, c’est que cette constante est la même pour toutes les transformations du même genre. On aurait pu prendre un sinus à la place de la fonction logistique, on aurait trouvé la même constante, c’est un truc universel !
Et d’ailleurs on retrouve la même chose pour l’ensemble de Mandelbrot que j’ai juste figuré via la vidéo de El JJ. On retrouve la constante de Feigenbaum comme ratio de taille de cercles successifs sur l’axe réel dans l’ensemble de Mandelbrot.
Chaos et Fractales
C’est du coup le bon moment pour commenter un peu plus les liens qui unissent la théorie du chaos et les fractales. Les deux sont très fréquemment associés, surtout dans la vulgarisation autour du sujet, mais le lien n’est pas si évident que cela à comprendre.
Tout d’abord, si vous connaissez par exemple l’ensemble de Mandelbrot, vous voyez qu’il existe au moins un lien : la notion d’itération successive d’une application. L’ensemble de Mandelbrot est définir à partir de la fonction du plan complexe
\(f_c(z) = z^2 + c\)
et consiste à regarder les valeurs de c pour lesquels l’itération répétée de la fonction \(f_c\) à partir du point z=0 ne diverge pas à l’infini.
Nous avons vu que dans le domaine des systèmes chaotiques, les fractales surgissent d’au moins deux façons :
- les attracteurs peuvent avoir une structure fractale (comme l’attracteur de Lorenz ou celui de Hénon)
- les diagrammes de bifurcation peuvent avoir une structure fractale.
De façon plus philosophique, on peut comprendre le lien entre fractales et systèmes chaotiques par l’idée générale que aussi proches que soient deux points dans l’espace, ils peuvent « être loin » du point de vue des propriétés. Dans le système chaotique, parce que l’évolution du système va les séparer de façon exponentielle. Dans les fractales parce que, par exemple, si on prend une courbe fractale (pensez à la côte bretonne), deux points très proches « à vol d’oiseau » peuvent se trouver à grande distance l’un de l’autre si on suit la courbe. (J’agite un peu les mains mais vous voyez l’idée).
Si on creuse un peu, on peut montrer que certains attracteurs étrange on une structure qui est en gros le produit d’un sous-espace « normal » par un sous-espace fractal du type « ensemble de Cantor« . C’est le cas d’ailleurs pour Hénon et Lorenz.
Ci-dessous un rappel de comment on construit l’ensemble de Cantor : on prend un segment, puis on enlève le tiers du milieu, et on itère.





51 Comments
Je crois que je suis le premier à feuilleter le billet avant la vidéo parce que la notification arrive avant. ^^
Pourtant je laisse 1min d’écart entre les 2 horaires de programmation !
j’ai deja fait un com sur youtube mais il ne sera surement pas lut alors je le remet ici.
Le fait que l’attracteur attire toujours au meme endroit quelque soit les condition initiale, ca ne voudrai pas dire que le fait que l’on réchauffe notre atmosphere ( rechaufement climatique ) n’aura aucune influance sur le climat ? on changera l ordre d’arriver des catastrophe mais on ne sortira pas le système de l’attracteur ?
et toujours sur le meme theme, comment expliquer que parfois le climat terrestre est completement sortie des « normes » ( la terre boule de neige par exemple ) vu ke tu a dit que toute les region de l attracteur sont transpercer autant de fois par les points il ne devrai donc pas y avoir de « zone rare » ou « extreme » et donc des période « boule de neige » de la terre devrais etre aussi courante que les autres, non ?
ou alors le climat terrestre est en fait simplement chaotique sans attracteur, si ca existe ? ( tu n as pas aborder ce point d’ailleurs, y a t il des systèmes complétement chaotique sans attracteur….
et au passage le lien pour ton billet de blog dans cette vidéo est erroné 😉
En fait c’est plutôt l’inverse. Le « climat » c’est l’attracteur, on peut battre des ailes, on modifiera la météo locale mais le climat global.
Par contre en déstabilisant la balance énergétique de la terre, on change les paramètres du système donc on déplace l’attracteur.
ça n’explique pas du tout la terre boule de neige ça… avant même que l homme intervienne les climats a fait des chose qui semble sortir d’un quelconque attracteur, a moins que la période de temps est été trop courte jusqu’ici pour avoir le temps de s’équilibrer autour d un attracteur, comme dans le tout début des simulation.
De plus changer « les paramètre du système » intuitivement ca ne me convainc pas, car les paramètres change constamment justement, le soleil a des cycle, l inclinaison de la terre change, notre magnétisme change, de temps a autre on se prend des météore sur la gueule, le système est loin d’être dans une bulle étanche, et l homme est loin d’être le seul a perturber le système. Je me demande donc si on peu vraiment prédire ce a quoi aboutira la pollution humaine… plus chaud ? plus froid? un emballement complet du système ? ou au contraire une plus grande stabilité ? j’ai l’impression que les climatologues sont loin de pouvoir prédire quoique se soit…
Cette réponse (« le climat c’est l’attracteur … et on le déplace » me permet de comprendre plein de choses derrière le terme utilisé de dérèglement climatique …
Lorenz n’a pris que trois variables ( pression, température, vitesse ) pour faire ses recherches, mais sur un système global, il y a bien d’autres facteurs comme l’axe de rotation de la terre par rapport au soleil ( qui détermine notamment les ères glaciaires/interglaciaires ) ou comme cette fameuse couche d’ozone dans notre atmosphère, sur lequel l’homme a un impact et qui peut être source d’un dérèglement climatique à échelle global.
Par contre, a priori, sur un système local où l’on ne considère que ces trois critères comme facteurs du climat, on retrouverais effectivement ce système chaotique avec ses attracteurs étranges.
Bon n’hésitez pas à me reprendre si j’ai raconté des conneries je suis qu’un petit étudiant de L2 ( pour trouver une excuse ) et j’en profite pour te remercier de cet énorme travail que tu as fait et que tu continue de faire David, accessible et ultra intéressant, j’ai souvent eu du mal à trouver ce genre de contenu sur le web.
Continue, je ne demande que ça !
Pour répondre à Luke (19h52) :
le climat terrestre étant régi par un grand nombre de paramètres, l’attracteur résultant est multidimensionnel et de forme sûrement très complexe. Une des ailes de celui-ci correspond sans doute à la Terre boule de neige, et manifestement il n’est pas atteint souvent ! De plus, il semblent que les paramètres ayant une influence sur la création d’une ère glaciaire sont d’ordre astronomique (et non terrestres), paramètres dont les modifications deviennent sensibles sur de longues périodes…
merci de ta reponse jean francois, mais alors ca veut dire que tout les points de l attracteur ne sont pas atteint avec la meme frequence ? apres j ai pas forcement tout compris a la video, mais j avais cru comprendre que justement chaque point etait atteint a la meme frequence, mais c’est peu etre seulement pour des cas particulier…
je me doute bien que l attracteur du climat doit etre monstrueusement complexe par raport a seulement 3 valeurs mais je pensais que le principe restait le meme. Par contre concernant la terre boule de neige, selon les theorie actuelle, rien a voir avec l astronomie, mais avec la biologie ! c’est l’apparition des cyanobactéries qui en rejetant de l oxygene crée la disparition du methane qui a l epoque etait tres presente et faisai un fort effet de serre, en disparaisant >>> gros refroidisement !
https://lejournal.cnrs.fr/articles/quand-la-terre-etait-une-boule-de-neige
bref j ai l impression que cette video ne s applique pas du tout au climat global de la terre… ca doit etre plutot une vulgarisation de la theorie du chaos avec un exemple de climat simplifier, mais on peut pas extrapoler ça au climat general… le climat a l echelle de la terre me semble bien plus « chaotique » lol et du coup ne peut pas etre modeliser par la theorie du chaos ?! ? je ne sait pas quoi en penser mais le climat terrestre ne semble pas reagir a une quelquon « theorie » et se contente d’evoluer en fonction de ce qui lui tombe sur la gueule ( apparition de la vie, augmentation rayonnement solaire, baisse de son energie interne, eruption volcanique, meteorite qui lui rentre dedans, pollution humaine, etc… )
Pingback: Effet Papillon et Théorie du Chaos — Science étonnante #52 | Blog de Nicolas Sellier - TV
Merci 😊
Bonjour David,
Je me permet de te tutoyer, c’est la mode sur la toile. Merci. Mille mercis de vulgariser tant de choses si passionnantes, si importantes,..
Vraiment, ton travail est admirable et très impressionnant. Garde la passion de tout cela, propage ton savoir et ton envie de savoir.
La terre ne s’en portera que mieux.
Il en faudrait plus des gens comme toi. Passionnés et doués. Bon j’arrête les compliments, tu vas faire une overdose.
Bonjour David,
Je me permet de te tutoyer, c’est la mode sur la toile. Merci. Mille mercis de vulgariser tant de choses si passionnantes, si importantes,..
Vraiment, ton travail est admirable et très impressionnant. Garde la passion de tout cela, propage ton savoir et ton envie de savoir.
La terre ne s’en portera que mieux.
Il en faudrait plus des gens comme toi. Passionnés et doués. Bon j’arrête les compliments, tu vas faire une overdose.
Merci David pour ton post
Pour ceux qui aiment le côté artistique :
http://www.chaoscope.org/ facile à paramétrer
qqes typos:
St-Ginglin -> St-Glinglin
$\approx 3.56995…$, à remettre en équation
Bonne continuation
Oups merci pour les coquilles, je corrige !
que certains attracteurs étrange on une structure –> …ont…
La vidéo est très sympa, mais je n’aurais pas pris le pendule simple comme exemple de système non-chaotique, justement parce que deux conditions initiales arbitrairement voisines conduisent à des états arbitrairement éloignés ! La période d’un pendule lâché avec une vitesse nulle dépend de l’angle initial et croit vers $+\infinity$ quand l’angle tend vers $\pi/2$… autrement dit deux pendules lâchés avec des vitesses nulles et des angles proches mais différents, oscillent avec des périodes proches, mais différentes, si bien qu’après un moment les deux pendules se trouvent dans des positions complètement différentes…
Pas faux : la sensibilité aux conditions initiales est là, mais toujours pas le côté imprévisible de l’évolution du système…
Salut Jacques-Olivier !
Oui tu as raison, je me suis laissé trop emballé par le pendule « des physiciens » où on linéarise le sinus !
J’espère que tu vas bien, au plaisir de se recroiser 🙂
Quand même à la réflexion je me demande si un pendule simple satisfait la condition de « mélange » des trajectoires (dans l’espace des phases). J’ai envie de penser que ça n’est pas le cas, et que du coup le système n’est pas chaotique (même s’il a une sensibilité aux conditions initiales)
Bonjour David,
Cela ne me semble effectivement pas le cas : une évolution dans l’espace des phase correspond en gros à un patatoïde (qui était circulaire quand on linéarisait le sinus), et si on prend un ensemble de conditions initiales on obtient une couronne de patatoïde. Les trajectoires, qui ne peuvent se couper, ne se mélangent donc pas. Je crois que le mouvement cyclique du pendule dans l’espace des phases empêche tout simplement l’aspect chaotique d’un système car la 2e condition ne sera jamais vérifiée..
Oui avec plaisir !! Dans l’espace des phases, le pendule ne melange pas beacoup en effet. Si on regarde une condition initiale vitesse=0 et angle $pi/2$ et qu’on note T la periode, puis qu’on prend un petit disque de l’espace des phases centre en $(0, pi/2)$ et qu’enfin on regarde le perimetre de l’image de ce disque apres T, 2T, 3T, etc. on obtient une suite (approximativement) arithmetique et pas geometrique. donc le pendule separe lineairement en temps des conditions initiales voisines. Techniquement, la differentielle du flot au temps T en $(0, pi/2)$ est une matrice triangulaire inferieure avec des 1 sur la diagonale. Dans l’ancien temps on appellait ca un glissement.
Et par ailleurs le flot n’est pas melangeant (pour la definition qu’on veut !) a cause ( ou grace ) a la conservation de l’energie !
Bonjour, et merci pour ce gros gros travail de compilation et de présentation.
Je suis enseignant et je me demandais :
Est-il possible qu’à l’occasion d’un cours, je projette tout ou partie d’une de tes vidéos afin d’amorcer un sujet, de provoquer un débat, en introduction d’un cours ? (que ce le soit ou pas, je vais te faire une pub d’enfer auprès de mes étudiants).
Merci d’avance pour ta réponse.
Bonjour Jean-François,
Oui avec grand plaisir ! Je suis ravi que cela serve à ce type d’usages,
David
Ok merci beaucoup !
Je n’en abuserai pas : mon objectif n’est pas de gagner du temps sur la préparation, mais par contre les étudiants méritent largement de connaitre ce qui se fait de mieux sur la toile ! (je sais : quel lèche-bottes…)
Pingback: Effet Papillon et Théorie du Chaos — Science étonnante #52 | VidShaker
Pingback: Effet Papillon et Théorie du Chaos — Science étonnante #52 – The Movie Zone – Action Movie Horror Movie Drama Movie Adult Movies & Series Movie
Pingback: Effet Papillon et Théorie du Chaos — Science étonnante #52 - NewsFlog
Merci David pour les .py
je sais que tu as dit que tu n’assurais pas le SAV
Je propose juste une adaptation pour ceux qui ont un PC/Windows
Donc, qqes modifs utiles pour le lecteur qui veut essayer tes fichiers
il faut modifier le chemin où est installé ffmpegexe et indiquer aussi celui de la sauvegarde
plt.rcParams[‘animation.ffmpeg_path’] = ‘e:/uz/ffmpeg/bin/ffmpeg.exe’
movie_file = ‘e:/temp/02-canon_poly.mp4’
ani.save( movie_file, writer = writer)
Pingback: Théorie du chaos et effet papillon | Science étonnante | Le blog d'Attila
un complément intéressant de la naissance du chaos, quand Henri Poincaré corrigé son erreur de l’article du pb des 3 corps
https://youtu.be/dpiNYrPasac
Après la vidéo (et le blog) je me suis posé la question « qu’est ce qu’un attracteur » ?
Je consulte donc Wikipédia qui me donne deux réponses :
1) une réponse intuitive qui est trop imprécise (un ensemble ou un espace vers lequel un système évolue de façon irréversible en l’absence de perturbations)
2) une réponse formelle qui dépasse mon niveau de math (Soit E un espace de Banach muni d’une mesure, Ω un …)
y a-t-il une définition moins formelle que la 2, mais plus précise que la 1 ?
Pingback: Effet Papillon et Théorie du Chaos — Science étonnante #52 | Science
Qu’ajouter à tous ces commentaires élogieux? Je trouve formidables les vidéos de la chaîne YouTube.
Je pensais être déjà sensibilisé au sujet du chaos déterministe et pourtant j’ai appris beaucoup de choses nouvelles avec la vidéo, les liens et dans ce billet.
Sans aucun doute la préparation a demandé un travail énorme, énormément de passion et un incroyable talent pour la vulgarisation scientifique.
Félicitations et un très grand merci!
Pingback: Effet Papillon et Théorie du Chaos — Science étonnante #52
Blog très intéressant, je me suis abonné.
Je n’ai pas vraiment d’arguments hormis le fait que je ne comprenne pas les équations, je vais rentrer en seconde et ce sont plus des sujets qu’on aborde en math sup./spé. Je n’ai pas encore vu la vidéo mais je me demandais si la vidéo explique plus clairement l’article haha.
Bonne journée à toi
Bonjour bonjour,
Je vais passer pour le relou typographique mais je reste embêté de voir la qualité du post égratignée par les <> LaTeX qui piquent les yeux.
A savoir : \frac{dx}{dt} est assez inadapté (on pourrait penser que d est une variable est pas une différentielle), mieux vaut utiliser \frac{\ensuretext{d}x}{\ensuretext{d}t}, de même pour exp (\exp{} et pas juste exp qui se lriait e fois x fois p)
Enfin f_\ensuretext{c} et pas f_c, mais ça à la limite ça reste anecdotique
Avec quelques macros bien mises on peut faire ça rapidement, ou même avec l’excellent package commath 🙂
C’est peut-être pinailler mais un peu de rigueur en LaTeX (et Dieu sait qu’il en manque dans les papiers de recherche) ne peut pas faire bien de mal !
$ merci si tu prends ça en compte, je conseille mathML ou mathjax pour rendre les équations et pas prendre dai foto $
Bonjour,
le raisonnement n’est pas clair sur le « quoi qu’on fasse » dans la vidéo ? Ou se trouve la limite si on imagine des ordinateurs assez puissants ?
Merci,
Pingback: Effet Papillon et Théorie du Chaos — Science étonnante #52 | Blog de Nicolas Sellier - TV
Pingback: Effet Papillon et Théorie du Chaos — Science étonnante #52 | JetBip
Bonjour,
J’ai été perdu très rapidement après le début du graphisme en 3D ! Je ne suis pas du tout bonne en maths, donc dès qu’il y en a un peu trop je décroche totalement.
Mais le début de la vidéo est très intéressante pour mon petit cerveau 🙂
Pingback: Replay Effet Papillon et Théorie du Chaos — Science étonnante #52 en streaming | Documentaire Société
Pingback: Documentaire Effet Papillon et Théorie du Chaos — Science étonnante #52 en streaming - Docu fr
salut, j espère que quelqu’un verra mon commentaire, pour la fonction chaotique 4x(1-x), vus que je ne crois jamais au hasard je me suis lancé dans la compréhension de la fonction, et si je me trompe pas, si on injecte 3/4 dedans, ça reste a 3/4, nombre attracteur (?). mon hypothèse c que il y a tjs des nombre attracteur, mais que la fonction est comment dire, pour 2x(1-x), elle est assez « calme » pour divergé tranquillement vers 1/2 , alors que pour 4x(1-x), elle est trop « rapide » pour reusire a se positionné sur 3/4… sauf si on lui injecte directe, mais du coup il doit y avoir moyen de prédire ce trop plein « d’activité » et de le mesuré, le système est-il encore chaotique a ce moment là ? voilà si je me trompe, dite moi ou. merci
En effet j’ai aussi trouvé ça mais je pense que ça n’enlève rien au côté chaotique de la suite, si on la fait partir à quelques milliardièmes de 3/4 elle s’en eloigne très vite. De plus 3/4 n’a pas d’autres antécédents que -1/4 et lui-même donc aucun risque de tomber dessus sans l’injecter volontairement
Encore moi en fait -1/4 n’est pas un antencedent de 3/4, d’ailleurs en fait chaque nombre (dans [0;1]) à deux antécédents un dans [0;1/2] et un dans [1/2; 1], de plus les les valeurs ( √5 + 5 )/ 8 et ( -√5 + 5 )/ 8 ocillent entre elles.
Excellent du coup maintenant je comprends pourquoi Lorenz a choisi l’analogie du papillon et pas un oiseau ou un insecte. J’avais entendu parler de son expérience mais je n’avais vu le modèle 3D d’évolution associé. En plus d’être un excellent scientifique, il était donc aussi doté d’un très bon sens de l’humour. Une belle private joke de scientifique !
Pingback: Effet Papillon et Théorie du Chaos — Science étonnante #52 – MovieCS