Aujourd’hui je voudrais vous parler d’une construction mathématique très jolie et injustement méconnue : les fractions continues.
Vous allez voir que les fractions continues sont à la fois simples, amusantes, belles et utiles !
Que demander de plus ?
Pi, ça vaut combien en gros ?
Même si vous n’êtes pas un super-geek, il est vraisemblable que vous connaissiez au moins les quelques premières décimales du nombre \(\pi\). L’écriture décimale d’un nombre comme \(\pi\), c’est un truc pratique mais forcément imparfait. En effet quel que soit le nombre de décimales qu’on choisisse de mettre, il ne s’agira que d’une approximation, qui n’est jamais exactement égale au véritable \(\pi\), par exemple
\(\pi = 3.14159265358979323846264338327950288419716939937510582…\)
Les fractions continues, c’est une autre manière de représenter et d’approximer des nombres réels, une alternative à l’écriture décimale.
Pour commencer, si on veut approximer \(\pi\) et qu’on est vraiment fainéant, on peut décider de laisser tomber les chiffres après la virgule et simplement dire que
\(\pi \approx 3\)
C’est un peu cru, alors voyons ce que l’on peut faire de mieux. \(\pi\) est égal à 3, plus un petit quelque chose
\(\pi = 3 + 0,1415926…\)
On peut décider de prendre l’inverse de ce petit quelque chose
\(\frac{1}{0,1415926…} = 7,062513…\)
et donc d’écrire
\(\pi = 3 + \frac{1}{7,062513…}\)
Si maintenant on laisse tomber ce qu’il y a après la virgule derrière le nombre 7, on obtient
\(\pi \approx 3 + \frac{1}{7}\)
Voilà qui est mieux que de simplement dire que \(\pi\) est égal à 3 !
Sauf que plutôt que de laisser tomber ce qu’il y avait après la virgule du nombre 7,062513, on aurait pu à nouveau inverser ce petit quelque chose et voir que
\(0,062513\cdots \approx 1/15\)
Si on injecte ça dans notre approximation, on obtient
\(\pi \approx 3 + \frac{1}{7+\frac{1}{15}}\)
Evidemment vous me voyez venir, on peut continuer à jouer à ce petit jeu plusieurs fois de suite et obtenir que
\(\pi=3 + \frac{1}{7+\frac{1}{15+\frac{1}{1+\frac{1}{292+\frac{1}{1+\ddots}}}}}\)
Je vous épargne les calculs qui mènent à cette écriture, mais vous noterez les points de suspension tout en bas : en fait on peut empiler les étages à l’infini sans que ça ne s’arrête jamais.
Une représentation des nombres réels
De manière générale, on appelle fraction continue une expression de la forme :
\(a_0 + \frac{1}{a_1+\frac{1}{a_2+\frac{1}{a_3+\frac{1}{a_4+\frac{1}{a_5+\ddots}}}}}\)
Ce qu’il y a d’intéressant, c’est que tout nombre réel peut s’écrire sous cette forme. Et réciproquement spécifier la suite des nombres entiers \(a_0, a_1, a_2, \cdots\) suffit pour reconstruire le nombre de départ. Il s’agit donc d’une manière nouvelle de représenter ou d’identifier un nombre réel.
Pour éviter de remplir des pages de fractions qui s’empilent, on utilise une notation plus compacte, on écrit simplement
\([a_0; a_1; a_2; a_3; \cdots]\)
Vous pouvez très bien voir cette écriture comme une alternative au développement décimal : plutôt que de spécifier un nombre en écrivant la suite de ses décimales, vous pouvez donner la suite de son développement en fraction continue.
Cette écriture a comme avantage qu’elle est indépendante du choix d’une base, alors que l’écriture décimale est bien sûr liée à la base 10 : en base 6 ou 23, les « décimales » de \(\pi\) seraient bien sûr différentes ! Mais le développement en fraction continue a plein d’autres avantages pratiques et esthétiques : commençons par la pratique.
Faire des approximations
Un truc que l’on fait tout le temps avec le développement décimal, c’est de le tronquer pour faire des approximations. Par exemple si j’écris \(\pi\approx 3,1415\), j’approxime \(\pi\) en tronquant son développement décimal.
Avec le développement en fraction continue, on peut faire pareil. Si on tronque le développement de \(\pi\) après le deuxième nombre, on obtient
\(\pi \approx [3;7] = 3 + \frac{1}{7}\)
Si je réduis le membre de droite au même dénominateur, cela donne
\(\pi \approx \frac{22}{7}=3.14285\cdots\)
qui est une fameuse approximation de \(\pi\). [Notez d’ailleurs que de fait le 22 Juillet (22/7) est un « Jour de \(\pi\) » bien plus légitime que le classique 14 Mars, qui lui aussi n’est finalement qu’une approximation, et en plus marche surtout pour les américains qui écrivent le mois avant le jour (3.14)]
Mais si je tronque plus loin le développement en fraction continue de \(\pi\), et après réduction au même dénominateur, j’obtiens d’autres approximations rationnelles (c’est-à-dire sous forme de fractions)
\(\pi \approx [3;7;15] = \frac{333}{106}=3.14150943396226\)
\(\pi \approx [3;7;15;1] = \frac{355}{113}=3.14159292035398\)
\(\pi \approx [3;7;15;1;292] = \frac{103993}{33102}=3.14159265301190\)
Alors vous allez me dire que l’écriture décimale fournit elle aussi des approximations rationnelles de \(\pi\), par exemple quand on écrit que \(\pi\) est égal à 3,1415, on écrit en fait que
\(\pi \approx \frac{31415}{10000}\)
Mais vous voyez qu’il faut aller chercher des dénominateurs et numérateurs très élevés, là où les approximations issues du développement en fraction continue utilisent des nombres bien plus petits.
En fait on peut même démontrer que les approximations rationnelles issues des fractions continues sont les meilleures possibles de toutes (« meilleures » dans le sens : tout approximation rationnelle meilleure que ça devra faire appel à des numérateurs et dénominateurs plus élevés).
L’approximation 355/113 de \(\pi\) est particulièrement intéressante, car elle est vraiment excellente (6 chiffres après la virgule) tout en utilisant un dénominateur pas trop grand
\(\frac{355}{113}=3,141592\cdots\)
Une des raisons pour lesquelles cette approximation est particulièrement bonne, c’est qu’elle est issue d’une troncation du développement en fraction continue effectuée juste avant un grand nombre (292), puisque
\(\pi = [3;7;15;1;292;1;1;2;1;\cdots]\).
Or si vous reprenez les constructions du début, vous constaterez qu’un grand nombre à un endroit donné du développement signifie un petit « pouillième » après la virgule. Bref si vous utilisez des fractions continues pour créer des approximations rationnelles de nombres réels, c’est en général une bonne idée de les couper juste avant un grand nombre.
Voilà, ça c’était pour l’intérêt pratique, passons maintenant à l’esthétique mathématique.
Quelques développements en fractions continues sympathiques
Un truc que vous savez peut-être (j’en avais parlé là), c’est que le développement décimal d’un nombre rationnel est périodique, par exemple
\(1/7=0,142857\ 142857\ 142857\ 142857\cdots\)
(ou tout du moins il fini toujours par être périodique). En revanche, il n’est que rarement fini (ça ne se produit que quand le dénominateur n’admet que 2 et/ou 5 comme facteur premier).
Au contraire le développement en fraction continue d’un rationnel est lui toujours fini. Et quand il est infini mais périodique, c’est que l’on a affaire à des nombres dits irrationnels quadratiques : ceux qui sont de la forme \(p+q\sqrt{N}\). Un exemple simple c’est \(\sqrt{2}\) dont le développement en fraction continue est enfantin
\(\sqrt{2} = [1;2;2;2;2;2;2;\cdots]\)
Mais le plus beau des développements en fraction continue est celui du célèbre nombre d’or
\(\phi = [1;1;1;1;1;1;1;1;1;\cdots]\)
Joli, non ?
Petite remarque au passage : on a dit que de grands nombres dans le développement signifiaient que le nombre s’approximait efficacement. Le fait que celui du nombre d’or ne contienne que des 1 implique que le nombre d’or est le nombre réel le plus difficile à approximer par des rationnels ! De là à dire que le nombre d’or a été créé par le Diable, il n’y a qu’un pas que je ne franchirai pas !
La constante de Khintchine
Je vais finir par une des propriétés les plus époustouflantes des développements en fractions continues. Prenez un nombre réel quelconque et calculez son développement en fractions continues
\(x=[a_0;a_1;a_2;a_3;…]\)
Maintenant effectuez la moyenne géométrique des n premiers termes du développement
\((a_0 a_1 a_2 a_3\cdots a_{n-1})^{1/n}\)
Si vous prenez de plus en plus de termes, c’est-à-dire que vous faites tendre \(n\) vers l’infini, la moyenne géométrique va toujours converger vers la même valeur
\((a_0 a_1 a_2 a_3\cdots a_{n-1})^{1/n}\to 2,685452\cdots\)
qu’on appelle la constante de Khintchine.
Incroyable, non ? Pourquoi est-ce que tous les développements en fractions continues de tous les nombres réels seraient-ils reliés entre eux ainsi ?
Moi ça m’épate…
Billets reliés
- Tout est dans pi : les nombres univers
- 0.999999999…, le nombre qui n’existe pas vraiment
- Quel est le plus grand nombre
possibleutile ?
Pour aller plus loin…
Première remarque avant d’aller plus loin : je sais qu’il existe un débat sur l’appellation correcte des fractions continues, certains mathématiciens recommandant de dire « fractions continuées » (ce qui d’ailleurs correspond mieux au terme anglais « continued fractions ».) Franchement je ne trouve pas que « fraction continue » soit un terme très bien choisi, mais « fractions continuées » n’étant pas tellement plus beau, je m’en tiendrai là.
Sur la constante de Khintchine, en fait la règle ne vaut pas pour tous les réels, mais pour *presque tous*, au sens mathématique de cette expression. C’est-à-dire que l’ensemble des nombres qui ne la vérifient pas est de mesure nulle (genre : les rationnels). Ce qui est drôle, c’est qu’on ne connait aucun nombre en particulier dont on soit certain qu’il vérifie la règle (eh oui je vous ai dit que ça marchait si vous preniez un nombre réel au hasard, mais je ne vous ait pas dit comment faire pour prendre un nombre réel vraiment au hasard !).
Enfin on peut généraliser un peu les fractions continues en autorisant des numérateurs autres que 1. On a alors des constructions du genre
\(a_0 + \frac{b_1}{a_1+\frac{b_2}{a_2+\frac{b_3}{a_3+\frac{b_4}{a_4+\frac{b_5}{a_5+\ddots}}}}}\)
Si on fait ça on perd bien sûr l’unicité du développement, mais il existe alors tout un tas de relations bizarres et fascinantes, je vous en pose quelques unes ici en guise de conclusion


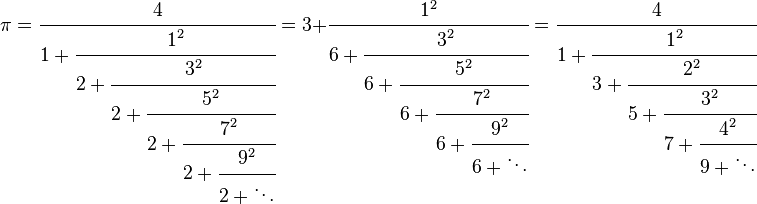




36 Comments
Heureusement, j’avais de l’aspirine sous la main !
La moyenne géométrique des n premiers termes ne converge pas « toujours » vers la constante de Khintchine. Mais « presque toujours » c’est à dire avec une probabilité 1. Ainsi, il est bien clair que cela ne fonctionne pas pour les nombres rationnels : le développement de 1/7 est [0,7,0,0,0,0,0,….] pour lequel la moyenne géométrique des n premiers termes tend vers 0. Le nombre d’or dont le développement est [1,1,1,1,…] n’a pas non plus cette propriété.
Mieux, on sait prouver que la moyenne géométrique des n premiers termes converge presque toujours vers cette constante mais on ne connait aucun exemple particulier !
Oui, oui. Tout ça était écrit dans l’article ! Il faut lire jusqu’au bout 🙂
Par contre du coup il vaudrait mieux remplacer « quelconque » par « aléatoire » car j’ai eu du mal à concilier les 2 paragraphes ! Aussi (c’est du pinaillage mais bon) $a_0$ ne doit pas etre inclus dans la moyenne.
Pas tout à fait, vous avez oublié de préciser ce qu’a bien précisé N. Gauvrit : ceci est vrai pour PRESQUE TOUS les réels, vous voye par exemple que ce n’est as le cas pour les tous les nombres dont vous donnez explicitement le développement. Et effectivement, on ne connait pour le moment aucune constante explicite qui vérifie cette propriété, et ca c’est réigolo 🙂
je vis dans La Voie Lacté, sur une planète Terre, plutôt en périphérie de notre galaxie, ici je pense qu’il s’agit d’êtres vivants sur une autre galaxie …bravo
Une petite réflexion personnelle suite a la lecture de cet article:
Il y a une bijection entre écriture décimale et développement en fraction continue, très bien. C’est à dire intuitivement, donner un nombre ou donner son développement en fraction continue, c’est la même chose.
Pour presque tous les nombres, la propriété de convergence vers la constante de Khintchine sur la fraction continue est vérifiée. C’est à dire intuitivement, il y a beaucoup plus de nombres pour lesquels cette propriété est vérifiée, que de nombres pour lesquels elle ne l’est pas.
Pour presque toutes les suites, la propriété de convergence de la moyenne géométrique des premiers termes vers la constante de Khintchine n’est pas vérifée. Intuitivement il y a beaucoup plus de suites qui ne vérifient pas cette propriétés que de suites qui la vérifient.
Tout ca semble bien paradoxal. Si je peux me permettre un parallèle, c’est comme si on avait la situation suivantes: 2 seaux contenant ayant exactement le même contenu : des pièces de monnaie, et exactement les même dans les deux seaux, mais l’un contient des pieces uniquement tournées sur le coté face, et l’autre des pièces uniquement tournées sur le coté pile. Si on pioche dans le seau contenant les piles, on est certain de trouver des pièces en euros. Si on pioche dans l’autre seau on est certain de trouver une pièce en n’importe quelle autre monnaie qu’un euro.
Comment est-ce possible?
Pour terminer le parallèle,
Ici on a le coté pile, le nombre dans son écriture décimale, le coté face, le nombre dans son développement en fraction continue, et la propriété d’etre en euros, la propriété de convergence de la moyenne géométrique des premiers termes vers la constante de Khintchine.
Cela illustre bien que lorsqu’il est question d’infini, la mesure est une propriété qui n’est pas intrinseque a l’ensemble, ni naturelle. C’est une notion plus riche que la cardinalité et le lien entre les deux est loin d’être évident
J’ai essayé d’expliquer dans cette vidéo (https://youtu.be/_V4GjyvDTfI) comment on peut explorer « géométriquement » le développement en fractions continues d’un nombre et le lien possible avec la croissance de certaines plantes. Peut-être trouverez-vous ça intéressant pour un prolongement…
Votre vidéo est étonnante, quel travail de réflexion et de réalisation !
J’irai voir http://cordier-phychi.toile-libre.org/phy/IPB.html, car il faut du temps pour digérer tout cela.
Si phi est intrinsèque à la nature, peut-être est-ce parce que son homomorphisme est économique ?
http://images.math.cnrs.fr/Mysteres-arithmetiques-de-la-suite.html
Sorkin écrit Ordre + Nombre = Géométrie
http://www.einstein-online.info/spotlights/causal_sets/?set_language=en
Avez-vous rencontré la constante de structure fine dans ce zoom qui pourrait éventuellement s’approcher de l’échelle de Planck ? Voilà aussi un ratio intéressant ~0.27/37, puisque
100α + (10α)^1/2 = 0,999871381
On peut même tenter un parallèle avec phi, pour le fun, (10α)^(-1/2)[(10α)^(-1/2) -1] ≈ dix
La dernière photo de la page http://cordier-phychi.toile-libre.org/phy/IPB.html, me fait songer à l’espace-temps et la matière, à l’attraction, l’interaction, ce miroir intrinsèque à l’unité x(x-1), tout comme celui qui caractérise le vide : l’unité epsilon_0*mu_0*c^2. Ainsi le positif d’Andromède http://urlz.fr/2kkx
Sans doute connaissez-vous aussi : https://youtube.googleapis.com/v/tnkLDFpgix4
Vu sous cet angle, la vie est bien belle.
Pingback: Les fractions continues | C@fé des Scien...
Alors là, je suis sidéré ! C’était un excellent article.
Je pensais que les fractions pour approximer Pi (comme 22/7) avaient été trouvé avant de connaitre les décimales de cette constante.
Aussi, je suis extrêmement impressionné par la constante de Khintchine, je ne la connaissais pas et je la trouve fascinante. D’après sa page Wikipédia, le développement en fraction continue de Pi vérifierait cette propriété. Plus impressionnant, le développement en fraction continue de la constante de Khintchine aurait une moyenne géométrique qui tendrait vers … La constante de Khintchine ! Je trouve ça magnifique et les dérivés de la fonction exponentielle n’ont cas bien se tenir.
Je pensais par ailleurs que tu allais parler des racines continues, elles sont bien mystérieuses elles aussi. je me demande si une constante de cette forme y est associée ? Genre un truc comme 2.685462… qui se cacherait dans ce genre de développement ?
> Je pensais que les fractions pour approximer Pi (comme 22/7) avaient été trouvé avant de connaitre les décimales de cette constante.
C’est le cas. 22/7 a notamment été découvert par Archimède (et sûrement par les Chinois de façon indépendante, à peu près à la même époque ou même avant), en tentant justement de trouver les décimales de pi.
Ce qui est dit dans l’article, c’est qu’à partir du développement en fractions continues, on peut justement retrouver ces approximations d’une toute autre manière, puisque Archimède avait par exemple utilisé des aires de polygones pour arriver à son résultat.
Pingback: Actualités et collectes mensuelles | Pearltrees
Bravo Dan pour cet article clair, qui a le mérite de faire connaître une très belle notion totalement absente des programmes depuis fort longtemps……quoique, à l’ UME, il y a 20 ans environ, mon collègue Francis Gutmacher avait animé un atelier sur ce sujet. Je ne connaissais pas « la constante de Khintchine », bien qu’ayant des connaissances non négligeables sur les fractions continues, acquises entre-autres en étudiant le « que sais-je » de Jean Itard « Arithmétique et théorie des nombres »…….
Mais je ne peux m’empêcher ici de dire que Evariste Galois (que je tiens pour ma part comme le plus grand mathématicien de tous les temps !) a, à 16 ans, publié dans les annales de Mathématiques de M.Gergonne, un théorème sur les fractions continues périodiques dont voici l’énoncé:
Théorème : Si une des racines d’une équation algébrique de degré quelconque est une fraction continue immédiatement périodique, cette équation aura nécessairement une autre racine également immédiatement périodique, que l’on obtiendra en divisant l’unité négative par cette même fraction continue périodique, écrite dans l’ordre inverse.
Il fallait déjà le voir !……Mais si vous avez des insomnies, essayez de le démontrer.
Notes historiques :
1) Galois commence sa démonstration par ces mots : « On sait que si, par la méthode de Lagrange, on développe en fractions continue une des racines…………. ».
2) Si certains se demande sur quoi je fonde l’opinion exprimée ci-dessus à son sujet, je les invite à lire le mémoire qu’il a adressé, à 19 ans et 3 mois, à l’ Académie des Sciences présidée par Siméon Denis Poisson.Ce dernier, aidé de Sylvestre Lacroix (tous deux majors de l’X et professeurs à l’X) a étudié ce mémoire.
Ils l’ont déclaré « inintelligible ». Si vous le comprenez, je vous dis « chapeau ». Sinon lisez l’article (de 30 pages environ, découpé par la rédaction en 5 articles) que j’ai publié dans TangenteSup n° 60.
J’espère avoir l’occasion de vous expliquer un jour pourquoi (par son caractère novateur et l’avance de 100 ans au moins qu’elle a sur les mathématiques de son époque, La Théorie de Galois est aux Mathématiques ce que la Théorie de La Relativité est à la Physique. Cela dit, imaginez qu’un jeune homme de 19 ans ai énoncé cette dernière, alors que Einstein, né 30 ans avant lui et mort 26 ans après lui, ne l’aurait même pas entrevue de toute sa vie !!!
C’est ce qui s’est passé pour Galois et sa théorie en remplaçant Einstein par Car Friedrich GAUSS !
Pour aller plus loin, voir sur BibNum un théorème très simple du jeune Galois 1829 (encore au lycée) https://www.bibnum.education.fr/mathematiques/algebre/demonstration-d-un-theoreme-sur-les-fractions-continues-periodiques (télécharger le PDF d’analyse par A. Juhel, graphie correcte).
Plus difficile, la façon dont Lambert en 1761 développe les fonctions trigonométriques en fractions continues dans sa démonstration de l’irrationnalité de PI (1761) https://www.bibnum.education.fr/mathematiques/theorie-des-nombres/lambert-et-l-irrationalite-de-p-1761
Comme vous l’indiquez, les fractions continues sont un très bel outil injustement négligé. Suite à l’article BibNum/Galois, fin 2011, nous devions avec mes co-auteurs animer un atelier de formation de profs du secondaire sur le sujet, en IUFM. Hélas pas entendu parler depuis.
Bonjour,
Merci pour cet excellent article. Vendredi je réfléchissais sur PI (et j’étais fort ennuyé par ces décimales qui semblent infiniment aléatoires et semblent nécessiter une mémoire infinie) et voici cet article qui arrive au bon moment. En regardant les développements de PI en fractions continues présentés à la fin de l’article et qui suivent un algorithme très simple et esthétique (nombres impaires au carré …), il me vient la réflexion suivante: Pi est ainsi décrit avec une précision infinie, en quelques mots, en quelques représentations. Si on veut plus de précision, il suffit de faire tourner l’algorithme un peu plus. La sensation qui me vient est celle des principes de compression d’image. De loin, une image grossière et plus on zoom plus les détails apparaissent et dans le cas de Pi avec un algorithme simple, la précision est donnée pour toujours (mais pour l’univers et les affichages proposés à nous pauvres humains, c’est pratique, « on » calcul juste ce dont on a besoin pour la précision/zoom demandés à un instant donné en fonction du besoin). Cela va bien dans le sens d’un univers cybernétique géré par quelques algorithmes simples.
Merci
Est-ce que les autistes qui énumèrent des heures de très nombreuses décimales de Pi se basent sur les fractions continues ? Sur la géométrie qui en découle ?
Si j’ai bien pigé, si on exprime la constante de Khintchine en fraction continue et qu’on calcule la moyenne géométrique des termes on retombe la constante de Khintchine ?
Et on ose dire que les maths sont chiante.
Bonjour,
Je voudrais savoir s’il existe une démonstration (j’imagine que oui) du développement en fraction continue de sqrt(2). Et de manière plus générale des irrationnels quadratiques.
Passionnant merci.
Au debut j’etais vraiment bluffe sur le fait que (presque) tous les developpement en fraction soient lies entre eux. En y reflechissant, ca ne vient pas vraiment d’un lien entre les reels, mais plus de la definition meme du developement en fraction continue, qui est une facon comme une autre de decrire un reel.
Par exemple, j’ai l’impression qu’on pourrait montrer de meme que la moyenne geometrique des chiffres de la decomposition decimale classique d’un reel tend quasiment toujours vers une constante non? Ce qui tient du fait que les chiffres sont equirepartis dans la decomposition decimale. [pour Pi : (3*1*4*1*5*9*…)^(1/n)]
Et la ca devient moins impressionant, cette limite montre juste que tous ces chiffres ont en commun une meme representation.
En tout cas, ca illustre bien a quel point on ne connait aucun nombre reel.
Pour le développement décimal, l’analogue serait surement la moyenne arithmétique qui elle tend vers 4.5 pour tout réel aléatoire (puisque les chiffres de 0 à 9 seront tous autant représentés)
« j’ai l’impression qu’on pourrait montrer de meme que la moyenne geometrique des chiffres de la decomposition decimale classique d’un reel tend quasiment toujours vers une constante non? »
C’est assez facile : il suffit qu’il y ait un zéro dans la décomposition décimale pour que la moyenne géométrique soit égale à zéro. Et le nombre de réel dont la décomposition décimale ne comporte pas de zéro est de mesure nulle.
Help ! En farfouillant sur wikipedia je tombe sur deux articles concernant l’un la constante de Khintchine ( https://fr.wikipedia.org/wiki/Constante_de_Khintchine ) et l’autre la constante de Lévy ( https://fr.wikipedia.org/wiki/Constante_de_L%C3%A9vy ) qui sont définies a priori de la même manière (sauf si je suis vraiment plus myope que je ne le pensais) mais en proposant deux valeurs numériques différentes : celle donnée sur ce blog pour la constante de Khintchine, et 3,2758… pour la constante de Lévy (alors que même définition).
Il y a bien une erreur ou c’est moi qui ai fumé ? Si c’est le cas il y a de l’édition qui va pas tarder 🙂
En fait dans un cas il y a un produit dans la limite et pas dans l’autre. J’avais donc mal lu ^^
Bravo Dan pour cet article clair, qui a le mérite de faire connaître une très belle notion totalement absente des programmes depuis fort longtemps……quoique, à l’ UME, il y a 20 ans environ, mon collègue Francis Gutmacher avait animé un atelier sur ce sujet. Je ne connaissais pas « la constante de Khintchine », bien qu’ayant des connaissances non négligeables sur les fractions continues, acquises entre-autres en étudiant le « que sais-je » de Jean Itard « Arithmétique et théorie des nombres »…….
Mais je ne peux m’empêcher ici de dire que Evariste Galois (que je tiens pour ma part comme le plus grand mathématicien de tous les temps !) a, à 16 ans, publié dans les annales de Mathématiques de M.Gergonne, un théorème sur les fractions continues périodiques dont voici l’énoncé:
Théorème : Si une des racines d’une équation algébrique de degré quelconque est une fraction continue immédiatement périodique, cette équation aura nécessairement une autre racine également immédiatement périodique, que l’on obtiendra en divisant l’unité négative par cette même fraction continue périodique, écrite dans l’ordre inverse.
Il fallait déjà le voir !……Mais si vous avez des insomnies, essayez de le démontrer.
Notes historiques :
1) Galois commence sa démonstration par ces mots : « On sait que si, par la méthode de Lagrange, on développe en fractions continue une des racines…………. ».
2) Si certains se demande sur quoi je fonde l’opinion exprimée ci-dessus à son sujet, je les invite à lire le mémoire qu’il a adressé, à 19 ans et 3 mois, à l’ Académie des Sciences présidée par Siméon Denis Poisson.Ce dernier, aidé de Sylvestre Lacroix (tous deux majors de l’X et professeurs à l’X) a étudié ce mémoire.
Ils l’ont déclaré « inintelligible ». Si vous le comprenez, je vous dis « chapeau ». Sinon lisez l’article (de 30 pages environ, découpé par la rédaction en 5 articles) que j’ai publié dans TangenteSup n° 60.
J’espère avoir l’occasion de vous expliquer un jour pourquoi (par son caractère novateur et l’avance de 100 ans au moins qu’elle a sur les mathématiques de son époque, La Théorie de Galois est aux Mathématiques ce que la Théorie de La Relativité est à la Physique. Cela dit, imaginez qu’un jeune homme de 19 ans ai énoncé cette dernière, alors que Einstein, né 30 ans avant lui et mort 26 ans après lui, ne l’aurait même pas entrevue de toute sa vie !!!
C’est ce qui s’est passé pour Galois et sa théorie en remplaçant Einstein par Car Friedrich GAUSS !
Très sympa, comme d’hab. Une typo : il fini toujours -> finit
Pingback: Rumbafan | Pearltrees
Oui, carrément bluffant…
D’ailleurs le résonnement pour arriver à la constante me fait un peu penser à celui ci:
https://www.youtube.com/watch?v=myZiR_yalwE
Le nombre e a une fraction continue avec une certaine périodicité aussi [2 ; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8…], c’est encore un truc bizarre et fascinant ou il s’agit d’un irrationnel quadratique? (je crois que ça se saurait si c’était le cas…)
Pingback: L'univers des nombres | Pearltrees
Merci pour cet excellent article, en le lisant une petite réflexion me vient à l’esprit.
Supposons un générateur aléatoire de nombres entiers strictement positifs, nous pouvons utiliser ce générateur pour définir une décomposition en fraction continue totalement quelconque qui elle même définit un nombre réel totalement quelconque.
Donc d’après Khintchine, la moyenne géométrique d’une suite composée d’entiers aléatoires devrait converger vers la constante de Khintchine? Vrai, faux ?
Je me suis également posé la question si l’on connaissait des règles arithmétiques pour manipuler directement des nombres représentés en fraction continue avec les opérateurs usuels. Ramanujan n’aurait il pas découvert certaines de ces règles qui lui auraient permis de jongler avec aisance avec cette puissante représentation?
Il me semble qu’il est délicat de parler de générateur aléatoire de nombres entiers strictement positifs comme ça (Comment fonctionnerait ce générateur ? Quelle serait la probabilité de tomber sur 49863 par exemple ?). Du coup il n’est pas sûr que l’on puisse parler de « décomposition en fractions continues totalement quelconque ».
Ceci dit les proba c’est hyper contre-intuitif et pas mon truc, donc peut-être qu’on peut définir un tel générateur et auquel cas la réponse à votre question serait « oui ».
Je reviens parasiter les commentaires pour évoquer une nouvelle vidéo que j’ai faite sur le sujet : https://youtu.be/zSnFffFo9bk
J’y introduis les fractions continues par l’intermédiaire de leur récursivité et de leur lien avec l’algorithme d’Euclide.
J’évoque ensuite 3 applications : les calendriers, les éclipses et les gammes (je détaille surtout la dernière).
Je ne suis pas vraiment en quête de popularité (vidéos sans son et pleines de texte) mais si celle-ci pouvait malgré tout toucher un petit public intéressé, son existence s’en trouverait bien mieux justifiée…
Désolé pour la méthode.
Pingback: Lionel | Pearltrees
Pingback: Curiosités sur les nombres | Pearltrees
Pingback: 4 (fausses) preuves de l’apocalypse : 1=2 – Jeux de maths, jeux de malins