 Depuis la défaite du champion du monde Gary Kasparov contre l’ordinateur Deep Blue en 1997, nous nous sommes habitués à ce que les machines soient définitivement plus fortes que les humains aux échecs. Bon après tout, les échecs, c’est rien que du pur raisonnement mathématique.
Depuis la défaite du champion du monde Gary Kasparov contre l’ordinateur Deep Blue en 1997, nous nous sommes habitués à ce que les machines soient définitivement plus fortes que les humains aux échecs. Bon après tout, les échecs, c’est rien que du pur raisonnement mathématique.
Mais le poker ? Ce jeu qui relève autant du calcul que de la psychologie, où il faut savoir entourlouper et bluffer, prendre des risques parfois, être prudent de temps en temps…un ordinateur battrait un champion du monde de poker ?
Eh bien les amis, sachez que la situation est encore bien pire que ça. Ce qui vient d’être annoncé il y a quelques jours, ça n’est pas qu’un ordinateur peut battre un humain, mais que cet ordinateur est capable de jouer une stratégie parfaite, et mathématiquement imbattable.
Résoudre les jeux
En termes techniques, on dit que le poker est maintenant un jeu résolu. Résoudre un jeu, cela veut dire trouver une stratégie qui permette à coup sûr de s’assurer la victoire. Bien sûr cette stratégie ne doit pas nécessairement être une suite de coups fixés à l’avance, mais plutôt une procédure pour réagir aux coups de l’adversaire tout en l’amenant à une défaite certaine.
 Pour expliquer ça, prenons un exemple simple : le jeu des bâtonnets. Ce jeu — rendu célèbre par l’émission de télé Fort Boyard — se joue de la façon suivante. Deux joueurs ont en face d’eux 20 petits bâtonnets. A chaque fois que c’est son tour, un joueur doit prendre 1, 2 ou 3 bâtonnets. Celui qui prend le dernier bâtonnet perd la partie.
Pour expliquer ça, prenons un exemple simple : le jeu des bâtonnets. Ce jeu — rendu célèbre par l’émission de télé Fort Boyard — se joue de la façon suivante. Deux joueurs ont en face d’eux 20 petits bâtonnets. A chaque fois que c’est son tour, un joueur doit prendre 1, 2 ou 3 bâtonnets. Celui qui prend le dernier bâtonnet perd la partie.
Eh bien si vous êtes le premier joueur, il existe une stratégie infaillible. Prenez 3 bâtonnets au premier coup, et ensuite si votre adversaire en a pris N, prenez en 4-N. Je vous laisse essayer pour vérifier que ça vous permet de fumer l’autre joueur à coup sûr !
Il faut noter que pour les jeux dans lesquels il peut y avoir « égalité », il n’existe pas forcément de stratégie infaillible assurant la victoire. Mais il en existe au moins une qui assure le match nul. C’est le cas par exemple du jeu de Morpion : si vous avez un peu l’habitude, vous pouvez très facilement faire en sorte que l’adversaire ne puisse pas gagner.
Il existe un tas de jeux simples qui sont aujourd’hui résolus. C’est par exemple le cas du Puissance 4, pour lequel il existe une stratégie permettant au premier joueur de gagner; mais aussi du jeu de Dames, dont la « résolution » a été publiée en 2007 [1].
A ce jour, le jeu d’échecs n’est pas encore résolu, et d’ailleurs il est peu probable qu’il le soit dans un jour proche. Donc actuellement quand les ordinateurs battent les humains aux échecs, ça n’est pas parce qu’ils disposent d’une stratégie mathématiquement parfaite : ils sont justes très très forts.
Les jeux à information incomplète
Les jeux comme les échecs ou le jeu des bâtonnets sont des jeux dits « à information complète ». Cela signifie que les deux joueurs possèdent tous les deux la même information : tout est sur la table, il n’y a rien de caché. Mais dans de nombreux jeux, on doit décider de son coup sans posséder toutes les informations : c’est ce qu’on appelle les jeux à information incomplète. D’ailleurs dans les décisions que l’on doit prendre dans la vie courante, nous n’avons jamais toutes les informations. John Von Neumann, un des pères de la théorie des jeux, disait d’ailleurs :
Real life is not like chess. Real life consists of bluffing, of little tactics of deception, of asking yourself what is the other man going to think I mean to do. And that is what games are about in my theory.
Le poker est certainement l’archétype de ces jeux à information incomplète. Au poker, on doit décider de son coup alors qu’il nous manque des informations cruciales : les cartes qui vont sortir bien sûr, mais surtout les cartes que possède l’adversaire !
La version du poker qui vient d’être résolue par le Computer Poker Research Group de l’université d’Alberta au Canada, c’est ce que l’on appelle le Heads up Limit Hold’em. Il s’agit d’un poker à deux joueurs, dans sa variante dite « limit », où la valeur de la relance est fixée, et le nombre de relances est limité. Dans cette version, chaque fois que c’est votre tour de jouer, vous n’avez que trois choix possibles : vous coucher, suivre ou relancer.
Le même groupe de recherche avait déjà créé dans le passé un programme du nom de Polaris, qui en 2008 fut le premier à battre des joueurs professionnels. Mais comme je vous l’ai dit, là nous sommes très au-dessus de ça puisque leur nouveau programme appelé Cepheus est mathématiquement imbattable : il joue une stratégie parfaite.
La stratégie de Cepheus ne résulte pas de l’ingurgitation de connaissances possédées par des experts du poker, mais d’une exploration du jeu que le programme a fait tout seul en jouant contre lui-même. En gros, il a essentiellement exploré toutes les situations possibles, et fabriqué une stratégie parfaite à partir de là. Pour cela, le programme a joué une moyenne de 6 milliards de parties par seconde pendant plus de deux mois. Autant dire qu’à chaque seconde, il a probablement joué plus de parties que l’humanité entière depuis l’invention du poker !
Dans le cas d’un jeu comme le poker, il est important de préciser ce qu’on entend par « une stratégie parfaite ». En effet étant donné qu’il y a un facteur chance dans le jeu, si vous jouez seulement 10 coups contre Cepheus et que vous avez une baraka d’enfer, vous allez peut-être gagner. Mais au long-terme, quand le facteur chance disparait du fait du grand nombre de parties jouées, c’est Cepheus qui gagnera à coup sûr.
Quelques enseignements
La stratégie mise au point par Cepheus ne se résume heureusement pas à quelques règles simples comme dans le cas du jeu des bâtonnets. Je dis « heureusement » car ça rendrait le poker un peu insipide si tout le monde pouvait jouer une stratégie parfaite. La stratégie est en fait tellement compliquée que pour la stocker il faut 11 Téra-octets de mémoire ! Mais si ça vous intéresse, vous pouvez vous rendre sur le site de Cepheus et lui soumettre une situation précise : vous saurez alors quelle est la décision optimale à prendre.
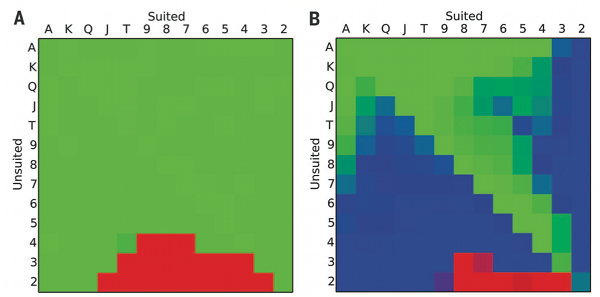
De l’analyse des premiers coups possibles, on peut tirer quelques enseignements intéressants pour les joueurs de poker. Par exemple Cepheus démontre mathématiquement ce que l’on savait par expérience : le donneur est avantagé car il joue en dernier. Autre leçon, vous pouvez consulter les décisions que prendrait Cepheus au premier tour en fonction des deux cartes initiales qu’il reçoit. Le graphique suivant est tiré de l’article [2]
Voici comment lire ce diagramme : à gauche, vous avez la stratégie à suivre en fonction de vos deux cartes initiales si vous êtes le premier à parler, à droite si vous êtes le second et que le premier joueur a misé. Vert = relancer, Rouge = se coucher, Bleu = Suivre. Si vos deux cartes sont de la même couleur, vous prenez la moitié supérieure droite du tableau, si elles sont de couleur différente, la moitié inférieure gauche.
Dans le tableau de gauche, on voit par exemple que si vous êtes le premier à parler, il ne faut jamais « checker » « caller » : soit vous y allez en relançant, soit vous vous couchez. Dans celui de droite, on voit que Cepheus ne se couche que si vraiment il est totalement en slip. Même avec un 3 et un 5 il va suivre !
Bien sûr pour les puristes il faut prendre ça avec des pincettes, car nous parlons ici de la version « Limit ». Comme on ne peut pas choisir le montant de la relance, cela enlève toutes les stratégies du genre « je relance de 100 000 ! ». Il n’est pas sûr que la stratégie de Cepheus puisse facilement s’adapter au « no limit ». Alors ok, les humains ont encore de beaux jours devant eux face aux machines !
Les plus grincheux vont nous dire : à quoi ça sert que des chercheurs soient payés à étudier les stratégies gagnantes au poker ! Eh bien chose amusante, dans l’article publié les auteurs concluent en justifiant des applications possibles de leur travail, et en citant les situations pour lesquels on se trouve dans une configuration proche des jeux à information incomplète, comme certaines enchères, ou même dans le cas de choix de traitement médicaux. Mais honnêtes, les auteurs terminent leur article par cette citation de Türing, autre père fondateur du domaine :
« It would be disingenuous of us to disguise the fact that the principal motive which prompted the work was the sheer fun of the thing »
Billets reliés
- Pierre-Feuille-Ciseaux dans la nature
- Le dilemme du prisonnier
- Axelrod et l’évolution de la coopération
- Deux stratégies révolutionnaires en théorie des jeux épisode 1 et épisode 2
- Chez Dr. Goulu : le poker : chance ou compétence ?
- ElJJ a parlé du jeu des bâtonnets sur Choux Romanesco
- Une vidéo de MicMaths pour gagner au jeu des bâtonnets
Références
[1] Schaeffer, Jonathan, et al. « Checkers is solved. » Science 317.5844 (2007): 1518-1522.
[2] Bowling, Michael, et al. « Heads-up limit hold’em poker is solved. » Science 347.6218 (2015): 145-149.





19 Comments
Les machines un jour pourront résoudre tous les problèmes, mais jamais aucune d’entre elles ne pourra en poser un ! (AE)
Tant que ce n’est pas prouvé…
L’article de recherche traîne sur mon ordi depuis plusieurs jours… Grâce à ce billet, je vais peut-être enfin trouver la motivation de le lire !
Il serait intéressant de noter, que contrairement aux autres jeux cités, le poker ne se limite pas à gagner ou perdre. On peut gagner un peu ou beaucoup, ou perdre un peu ou beaucoup. Et ça, ça a une conséquence notable : c’est surtout contre la stratégie de Cepheus que la stratégie de Cepheus est la meilleure (oui, vous avez bien lu!).
Je m’explique. Si la stratégie de l’adversaire n’est pas celle de Cepheus, il existe en général des stratégies contre l’adversaire qui sont meilleures que celle de Cepheus. En particulier, si l’adversaire est le donneur mais n’a pas le niveau de Cepheus, il est possible que Cepheus perde contre lui, mais qu’une autre stratégie batte l’adversaire.
Quand on dit que la stratégie de Cepheus est parfaite, ce que l’on entend, c’est qu’il s’agit d’un équilibre de Nash. Ou plus exactement, comme il s’agit d’un jeu à 2 joueurs à somme nulle, de stratégies optimales au sens de von Neumann. Ça veut dire que, contre toutes les stratégies possibles de l’adversaire, la stratégie de Cepheus assure le meilleur gain dans le pire cas. C’est en cela qu’elle est parfaite : si l’adversaire est infiniment intelligent, c’est bien la stratégie de Cepheus qu’il faut jouer.
Voilà, j’espère que ça peut un peu éclairer les choses. Bon, pendant ce temps, moi, je vais me mettre à lire l’article de recherche !
Et pour illustrer ce point, on peut utiliser le simple jeu de pierre-feuille-ciseaux. Ici la stratégie inexploitable (impossible de gagner contre celle ci) est le choix aléatoire. C’est ce que ferait Cepheus. Contre toute autre stratégie, elle assure une espérance nulle. Mais dans le cas où l’autre joueur adopte une stratégie, donc un tirage non aléatoire, alors la stratégie de Cepheus n’est pas optimale au sens où ce n’est pas la stratégie qui maximise l’espérance. Pour maximiser l’espérance il faut alors définir une contre stratégie qui exploite l’information des parties précédentes.
Le « bot » par une petite intelligence artificielle peut alors construire une stratégie plus performante que celle de base (tout aléatoire) tout en restant imbattable. Explication et démonstration avec un jeu :
http://www.nytimes.com/interactive/science/rock-paper-scissors.html
Ainsi sur une table de poker avec trois joueurs avec Cepheus, un mauvais joueur et un bon joueur, le bon joueur pourrait avoir une espérance plus élevée que celle de Céphéus car il exploite mieux les faiblesses du mauvais joueur. Mais si celui part, alors il peut au mieux ne pas perdre d’argent contre Cepheus.
Les très bons joueurs de poker sont maintenant très bons sur ces aspects.
En headup le premier joueur ne peut pas checker ! Vu qu’il doit compléter call…
Ça dépend, si on se trouve pré-flop le premier joueur doit au minimum call, si il est post-flop il peut check 🙂
Oui on parle du pré-flop, donc manifestement je me suis trompé de terme !
La leçon est donc que Cepheus ne « call » jamais quand il est premier joueur. Il se couche ou il relance.
la vraie question c’est : est-ce qu’on peut l’utiliser pour tricher sur les sites de poker en ligne? 😉
Salut,
Merci pour ton billet. J’étais passé à côté de cette info. Une question et quelques remarques.
1) Pourrais-tu préciser en quel sens précis sa stratégie est la meilleure ? Est-ce que cela signifie que, quelque soit la stratégie (éventuellement évolutive ?) de l’adversaire, la limite supérieure du gain moyen sur un grand nombre de partie est supérieur ou égal à 0 ?
2) « Bon après tout, les échecs, c’est rien que du pur raisonnement mathématique. » En tant que matheux, ce genre de formulation me fait toujours un peu grincer des dents :-). Cela dit je me demande ce que tu veux dire exactement. Que ce soit du côté humain ou du côté ordinateur, il est hors de question d’explorer tout l’arbre des coups possibles. Par ailleurs, du côté humain, il y a réellement un facteur humain : tu ne joues pas toujours ce qui est considéré comme le meilleur coup, tu essayes aussi d’amener ton adversaire sur une position où tu es meilleur que lui (que ce soit parce que cela correspond mieux à ton style de jeu, parce que la position est simple pour toi et complexe pour l’adversaire, ou parce que tu as étudié au préalable les positions en question et que tu espères que ton adversaire n’en a pas fait autant etc.). Il y a aussi la gestion du temps sur une partie, la gestion de la fatigue sur plusieurs parties successives, …
3) Il me semble que le jeu de dame résolu est le jeu de dames anglaises (en particulier c’est sur une grille 8*8 et non 10*10).
4) Il y aurait peut-être un billet intéressant à faire sur le jeu d’othello. De mémoire, les logiciels ont fait un grand bon en qualité quand ils ont commencé à intégrer de l’aléa dans l’exploration de l’arbre des possibles. Pour caricaturer : le logiciel explore tout l’arbre des possibles jusqu’à un certain niveau puis, à partir de là, joue des coups au hasard et évalue la position finale. Je trouve ça assez bluffant comme idée.
A propos du jeu d’échecs, un passage intéressant dans le livre « Aventures au coeur de la mémoire » (J.Foer) : on a montré que, quand il s’agit de mémoriser la position des pièces sur l’échiquier, les grands maîtres sont évidemment bien meilleurs que ceux qui ne connaissent pas le jeu… sauf si la position des pièces n’est pas possible dans une partie ! En d ‘autres termes (et avec plus d’arguments développés, voir le bouquin) la victoire aux échecs dépend en grande partie de la mémoire inconsciente, donc du nombre de parties jouées .donc je pense que pour n’importe quel jeu, les « intelligences artificielles » modernes finiront par nous battre partout, simplement parcequ’elles ont plus de ..mémoire.
Pingback: https://sciencetonnante.wordpress.com/2015/01/19/une-strategie-infaillible-au-poker/
Pingback: Une stratégie infaillible au poker | EDM...
Pingback: Une stratégie infaillible au poker ! | T...
« pour les puristes il faut prendre ça avec des pincettes, car nous parlons ici de la version « Limit ». »
Il ne s’agit pas d’être « puristes » ou non.
L’ensemble de l’article est trompeur car il laisse à penser que le poker est résolu (sauf pour les « puristes »).
Alors qu’en fait, cela n’est pas du tout le cas pour la version « No limit », qui est la version la plus joué.
Seul le Limit en Head’s up est résolu, cela concerne une partie « infime » du poker, et même pour un public « non puristes » qui ne comprend pas la différence, il est totalement faux de laisser penser que le poker est « résolu ».
C’est un peu comme de dire « J’ai programmé une Intelligence Artificielle de résoudre tous les exercices de Maths de tous les livres que l’on pourra lui présenter ».
Bien sûr pour les puristes, je parle uniquement des livres du programme de 6ème.
Sinon, comme dit dans un commentaire plus haut : le but du poker n’est pas d’avoir une stratégie « inexploitable » mais bien d’avoir une stratégie « exploitante », c’est à dire trouver les failles dans le jeu adverse et les exploiter. Et cela, une machine ne le ferra jamais aussi bien qu’une intelligence humaine.
Prenez deux joueurs jouant une stratégie purement parfaite au poker, mettez-les en face à face dans un casino : Ils seront tous les 2 perdants à cause du prélèvement du Casino.
Autrement formulé :
Non seulement l’article ne traite que d’une partie infime du poker (Limit et non No limit et HU et non table à 6 ou 9 joueurs) mais en plus, il explique un truc qui ne sert à rien : A savoir au poker avoir la garantie que l’on ne peut pas être battu par une autre stratégie ; alors que le but du poker est d’avoir une stratégie qui écrase le plus possible son adversaire. (à cause de la variance et du « rake » être « à jeu » ou « un peu mieux qu’à jeu » ne sert strictement à rien !
Si vos deux cartes sont de la même couleur, vous prenez la moitié supérieure droite du tableau, si elles sont de couleur différente, la moitié inférieure gauche
Bonjour
je ne comprend pas la phrase que j ai mis elle fait partie de l article
les situations possibles)