 Quand on parle du développement de l’aéronautique, on évoque généralement le fait que « de tout temps les hommes » ont toujours été fascinés par la capacité des oiseaux à voler. Mais c’est oublier que les insectes avaient inventé le vol longtemps avant les oiseaux !
Quand on parle du développement de l’aéronautique, on évoque généralement le fait que « de tout temps les hommes » ont toujours été fascinés par la capacité des oiseaux à voler. Mais c’est oublier que les insectes avaient inventé le vol longtemps avant les oiseaux !
Bien que le spectacle soit moins majestueux, il faut reconnaitre que les insectes sont encore plus forts que les oiseaux, j’en veux pour preuve la difficulté qu’il y a à attraper des mouches ou à écraser des moustiques.
Et pourtant si on s’en réfère aux lois classiques de l’aérodynamique, les insectes ne devraient pas pouvoir voler ! S’ils y arrivent quand même, c’est que leur vol se base sur des principes physiques assez différents de ceux qui gouvernent un Airbus ou un corbeau.
Le vol des insectes
A bien des égards, les insectes peuvent être vus comme les vrais maîtres de la planète. Il en existerait quelques millions d’espèces, et on compterait sur Terre pas loin de \(10^{19}\) insectes, soit un milliard d’insectes pour chaque être humain (imaginez les dans votre lit) [1].
Leur capacité à voler n’est certainement pas étrangère à ce formidable succès évolutif : le vol permet aux insectes de se disséminer bien sûr, mais aussi de trouver de la nourriture, de se défendre, et même de communiquer ou de se faire la cour.
On oublie d’ailleurs souvent que les insectes furent les premiers animaux à savoir voler, il y a environ 350 millions d’années. Après eux, seuls trois autres groupes – les ptérosaures, les chauves-souris et les oiseaux – y sont parvenu de manière indépendante. Mais aucun ne maîtrise le vol aussi bien que les insectes, qui sont capables de prouesses comme de soulever l’équivalent de leur poids, ou de réaliser des vols stationnaires impeccables, ce dont sont incapables les oiseaux.
Mais ce qu’il y a de plus surprenant dans l’affaire, c’est qu’en théorie, les insectes ne devraient pas arriver à voler ! Si on leur applique les lois qui expliquent le vol des oiseaux ou des avions, on trouve qu’ils ne devraient même pas pouvoir se maintenir en l’air. Pour comprendre le vol des insectes, il faut faire appel à des principes nouveaux, différents de ceux que l’on utilise en aéronautique classique.
Comment un avion vole-t-il ?
Avant de passer au cas compliqué de l’insecte, revoyons l’explication habituellement donnée pour expliquer la manière dont volent les avions.
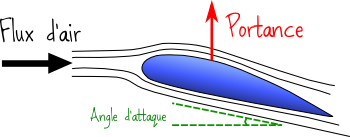 Quand une aile d’avion se déplace, le flux d’air qu’elle traverse se trouve séparé en deux composantes, et l’air circulant au-dessus de l’aile possède une vitesse plus élevée que celui circulant en-dessous. Ceci crée une dépression, qui provoque sur l’aile une force, dont la composante dirigée verticalement est appelée la portance. C’est la portance qui permet à l’avion de rester en l’air et de s’opposer à la gravité.
Quand une aile d’avion se déplace, le flux d’air qu’elle traverse se trouve séparé en deux composantes, et l’air circulant au-dessus de l’aile possède une vitesse plus élevée que celui circulant en-dessous. Ceci crée une dépression, qui provoque sur l’aile une force, dont la composante dirigée verticalement est appelée la portance. C’est la portance qui permet à l’avion de rester en l’air et de s’opposer à la gravité.
Un paramètre important dans le vol des avions est ce qu’on appelle l’angle d’attaque (voir ci-dessus). Généralement, plus l’angle d’attaque est élevé, plus la portance sera importante. En jouant avec l’orientation de l’avion on peut augmenter l’angle d’attaque et donc la portance. Mais il y a une limite ! Avec les formes d’ailes usuelles, quand l’angle d’attaque atteint environ 15°, l’air commence à ne plus s’écouler correctement autour de l’aile, des turbulences se forment et la portance disparaît : on dit que l’avion décroche.
 Passons maintenant aux oiseaux. Cela peut vous surprendre au premier abord, mais ils fonctionnent selon le même principe ! Je vous vois venir d’ici, vous allez me dire « Oui mais l’oiseau il bat des ailes, patate ! ». Bien sûr, mais les lois physiques en jeu sont les mêmes.
Passons maintenant aux oiseaux. Cela peut vous surprendre au premier abord, mais ils fonctionnent selon le même principe ! Je vous vois venir d’ici, vous allez me dire « Oui mais l’oiseau il bat des ailes, patate ! ». Bien sûr, mais les lois physiques en jeu sont les mêmes.
La théorie aérodynamique classique s’applique à une aile placée dans un fluide en mouvement autour d’elle. Dans le cas de l’avion, le mouvement est simple (une translation), et dans le cas des ailes de l’oiseau il est plus compliqué. Mais si vous décomposez le mouvement des ailes d’un oiseau, à chaque instant vous pouvez calculer la vitesse de l’air et l’angle d’attaque, et déduire la portance obtenue comme pour un avion.
Si vous n’êtes pas convaincus de la similarité entre les oiseaux et les avions, pensez que pour un hélicoptère on peut faire exactement le même calcul : les pales sont aussi des ailes mises en mouvement par rapport à l’air (avec un mouvement encore différent), et qui engendrent une portance que l’on peut calculer selon les mêmes lois.
Pourquoi (en théorie) les insectes ne peuvent pas voler
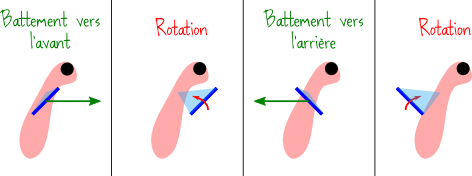
Pour voir si la théorie classique s’applique aussi aux insectes, on peut examiner le mouvement de leurs ailes et calculer la portance que l’on obtient, de la même manière qu’on le ferait pour un oiseau. Première chose surprenante, les insectes possèdent souvent 4 ailes, et les battent généralement d’avant en arrière et pas de haut en bas. A chaque extrémité de la trajectoire, ils effectuent une rotation de leurs ailes, comme le montre le petit schéma ci-dessous :
Ensuite il y a une chose qui devrait vous frapper sur ce schéma : l’angle d’attaque. Chez les insectes, il est typiquement de 25 à 45°. Comme je vous le disais plus haut, des angles d’attaque aussi élevés sont totalement incompatibles avec le vol classique : ils engendrent des turbulences qui détruisent la portance et provoquent le décrochage. Conclusion : vu comme ils s’y prennent, les insectes ne devraient pas arriver à voler. Et pourtant…ils y arrivent ! Il y a donc quelque chose à comprendre.
Les esprits chagrins pourront se demander quel intérêt il y a à étudier le vol des mouches et autres libellules. Et pourtant c’est une énigme fascinante ! L’homme a mis des millénaires à pouvoir créer de la portance à la manière des oiseaux, et voici que l’on découvre qu’il existerait une autre façon de le faire !
Pour mieux comprendre le vol des insectes, les scientifiques ont eu recours à tout un tas de techniques : observer des mouches attachées par un fil, utiliser des caméras rapides, placer des ailes d’insectes dans des mini-souffleries, etc. Mais l’une des méthodes les plus efficaces a été de faire des maquettes d’insectes à grande échelle.
Comment faire une maquette d’insecte ?
Grâce aux microscopes et aux caméras rapides, il est assez facile d’observer un insecte pour recréer un modèle de grande taille, qui reproduit précisément son anatomie et les mouvements de ses ailes. Mais pour comprendre les phénomènes aérodynamiques en jeu, cela ne suffit pas. Et la raison s’appelle le nombre de Reynolds.
J’ai déjà eu l’occasion d’écrire un billet sur le nombre de Reynolds, mais j’en rappelle ici les grandes lignes. Quand un fluide s’écoule, il peut le faire de manière calme et ordonnée (comme de l’huile sortant du goulot d’une bouteille), ou de manière turbulente, comme l’eau d’un fleuve autour des piles d’un pont. Pour savoir dans laquelle des deux situations on se trouve, on peut calculer le nombre de Reynolds, qui est obtenu selon la formule
Plus le nombre de Reynolds est élevé, plus l’écoulement est turbulent. Pour un avion, il est de l’ordre de quelques millions, alors que pour un insecte il sera plutôt autour de 1000. Du point de vue de la mécanique des fluides, ce sont deux situations très différentes ! Morale de l’histoire : si vous voulez comprendre l’aérodynamique des insectes en faisant une maquette, il faut que celle-ci possède le même nombre de Reynolds que l’insecte de départ.
 Observez la formule : si votre maquette est beaucoup plus grosse que l’insecte, il faut diminuer la vitesse et/ou augmenter la viscosité pour que l’expérience soit représentative. C’est ainsi que l’équipe de Michael Dickinson à Berkeley a créé Robofly : une maquette de 60 cm d’envergure (ci-contre), mais battant des ailes bien très lentement – toutes les 5 secondes – et baignant dans de l’huile très visqueuse [2]. C’est grâce à la réduction de la vitesse des ailes et l’augmentation de la viscosité du fluide qu’ils ont pu produire une maquette représentative du vol des insectes (c’est-à-dire à nombre de Reynolds comparable), et comprendre ainsi les phénomènes en jeu.
Observez la formule : si votre maquette est beaucoup plus grosse que l’insecte, il faut diminuer la vitesse et/ou augmenter la viscosité pour que l’expérience soit représentative. C’est ainsi que l’équipe de Michael Dickinson à Berkeley a créé Robofly : une maquette de 60 cm d’envergure (ci-contre), mais battant des ailes bien très lentement – toutes les 5 secondes – et baignant dans de l’huile très visqueuse [2]. C’est grâce à la réduction de la vitesse des ailes et l’augmentation de la viscosité du fluide qu’ils ont pu produire une maquette représentative du vol des insectes (c’est-à-dire à nombre de Reynolds comparable), et comprendre ainsi les phénomènes en jeu.
Le secret des effets transitoires
Grâce aux modèles réduits comme Robofly, les chercheurs ont pu lever une partie du mystère qui entoure le vol des insectes. Le premier de ces effets s’appelle le décrochage retardé. Je vous l’ai dit, avec des angles d’attaque de 25 à 45°, les ailes des insectes devraient provoquer un décrochage. Mais ce qu’ont constaté les chercheurs, c’est que pour les insectes, ce décrochage n’a pas le temps de se produire complètement, et c’est même lui qui les aide à obtenir leur portance.
Il s’agit en fait d’un phénomène qui était apparemment connu pour les avions depuis les années 30. Quand un décrochage se produit, un tourbillon se forme au bord de l’aile et très rapidement se détache, provoquant la perte de portance. Mais pendant un court instant, l’air mis en mouvement rapide par le tourbillon provoque une dépression transitoire qui fournit un petit bonus de portance.
Pour un avion, il est impossible d’exploiter ce phénomène car il est trop rapide, mais à l’échelle de l’insecte, cela fonctionne grâce à la fréquence de battement de ses ailes. En gros en se mettant en permanence en situation de décrochage, l’insecte arriver à collecter tous ces petits bonus de portance, ce qui lui permet de se maintenir en l’air.
Depuis, d’autres phénomènes transitoires de même type ont été mis en évidence, et ils concernent le rôle de la rotation des ailes (qui fournit aussi de la portance) et du mouvement d’aller-retour qui permettrait à l’insecte de recycler ses propres turbulences pour l’aider à se maintenir [2].
Grâce à la découverte de ces principes, il est maintenant possible de réaliser des robots miniatures dont le fonctionnement se rapproche de plus en plus de celui de nos amis les insectes [3]. On peut facilement imaginer les applications de ce genre de technologie en matière de sauvetage, d’exploration mais aussi bien sûr de surveillance plus ou moins discrète…
Billets reliés, ici ou ailleurs…
- Mon billet sur le nombre de Reynolds, pour en savoir un peu plus sur le sujet
- L’équation de Navier-Stokes, ou pourquoi la mécanique des fluides c’est dur
- Un billet de Taupo sur le blog SSAFT, qui nous parle des différents moyens de locomotion des insectes (avec plein de vidéos sur leur vol)
- Un billet traduit par Dr Goulu sur la vie à faible nombre de Reynolds (plutôt les bactéries qui nagent que les insectes qui volent)
Pour aller plus loin
Premier point pour aller plus loin, la portance des ailes d’avion provient du fait que l’air circule à vitesse plus élevée sur la face supérieure que sous la face inférieure de l’aile. Parfois, on entend que c’est parce que l’air doit mettre le même temps au-dessus et en-dessous, et doit donc aller plus vite car le chemin est plus long par au-dessus. Eh bien c’est faux ! En général, il n’y a pas de raison pour que le temps de transit de l’air soit identique dans les deux chemins. Et même la plupart du temps, il est plus rapide par au-dessus ! Cela se voit bien sur l’animation ci-dessous, ou l’on constate que l’air passé au-dessus arrive très en avance par rapport à celui passé en dessous.
Pour les fans du vol des insectes, un papier récent dans Science [4] a montré que pour échapper à une menace, ils utilisent des mouvements qui ne sont pas sans rappeler ceux des chasseurs. Pour changer de direction en situation normale, les insectes utilisent le phénomène du lacet : une rotation autour de l’axe vertical. C’est ce que font les avions quand ils agissent sur la gouverne de direction.
Mais en présence de menace, ils peuvent en l’espace de quelques millisecondes changer de direction au moyen d’une combinaison de roulis et de tangage. Avec ce genre de manoeuvre façon Top Gun, pas étonnant qu’on n’arrive pas à les attraper !
Références
[1] Entomological society of America FAQ
[2] Dickinson, Michael. « Solving the mystery of insect flight. » Scientific American 284.6 (2001): 48-57.
[3] David Lentink, Biomimetics: Flying like a fly, Nature 498, 306–307 (2013)
[4] Florian T. Muijres et al., Flies Evade Looming Targets by Executing Rapid Visually Directed Banked Turns, Science 344, 172 (2014)
Crédits
- Libellule, Wikimedia Commons
- Portance et angle d’attaque, réalisé d’après ce schéma, Wikimedia Commons
- Schéma du vol des insectes : Science étonnante
- Cygne en migration, Wikimedia Commons
- Robofly, (C) Université Berkeley
- Animation de circulation de l’air, Wikimedia commons






29 Comments
http://www.grc.nasa.gov/WWW/k-12/airplane/wrong1.html
On m’a menti pendant mes années de prépa !
Bonjour David, voici un lien intéressant après une brève recherche sur google:
http://mesvideos.croire.com/video/iLyROoafILw0.html
À bientôt
Merci pour cet article parfaitement explicatif, et la mention du billet de SSAFT!
Bonjour,
Si l’on arrivait a diminuer fortement la viscosité de l’air dans une pièce suffisamment hermétique, est-ce que mouches et moustiques se retrouveraient cloués au sol ?
Bonne question. Ca doit dépendre de la vitesse de décrochage des tourbillons rapportée à la fréquence de battement des ailes. J’ai envie de penser que les tourbillons vont effectivement se décrocher plus vite si la viscosité baisse.
On n’a qu’à essayer avec le colibri, qui apparemment emprunte « de justesse » des mécanismes de portance aux insectes.
Merci pour le lien 😉
Sur la portance « normale » tu dis fort justement « Parfois, on entend que c’est parce que l’air doit mettre le même temps au-dessus et en-dessous, et doit donc aller plus vite car le chemin est plus long par au-dessus. Eh bien c’est faux ! « . Mais tu ne dis pas ce qui est juste …
Dans cet article http://www.drgoulu.com/2012/03/11/portance-pourquoi-ca-vole/ j’ai résumé 3 autres articles d’un pote ( Frédéric Monsonnec ) qui font un grand tour historique des théories de la portance. Mais je ne suis toujours pas convaincu de la justesse de la « théorie de l’écope de Newton » admise par la NASA selon laquelle l’aile dévie de l’air vers le bas, ce qui engendre une force par F=m.a. D’ailleurs, sur ta jolie illustration animée (trouvée où?), on ne constate pas de déplacement vertical des filets d’air derrière l’aile par rapport à devant …
Il me semble qu’un argument contre l’écope de Newton (si je comprends bien) est que dans cette théorie la portance évolue en $latex (\sin \alpha)^2$ (l’angle d’attaque est $latex \alpha$) alors que dans l’expérience (et la théorie correcte) ça évolue essentiellement en $latex \sin \alpha$.
Sinon l’animation vient de Wikimedia Commons, le lien est à la fin du billet (oui, j’ai pris plein de bonnes résolutions récemment, et je crédite les illustrations :-))
J’adore votre plume ! J’ai eu quelques frissons en regardant mon lit, et chacun de vos billets sont très instructifs.
Pingback: Comment les insectes font-ils pour voler ? | C@...
Cet article me conforte dans mon profond respect pour la mouche à décollage vertical.
Bien comprendre le mouvement renforce l’efficacité du jeu du poignet avec la tapette.
Pingback: Comment les insectes font-ils pour voler ? | Cu...
Pingback: Comment les insectes font-ils pour voler ? | En...
Pingback: Comment les insectes font-ils pour voler ? | Et...
« Quand une aile d’avion se déplace […] l’air circulant au-dessus de l’aile possède une vitesse plus élevée […]. Ceci crée une dépression, qui provoque sur l’aile une force, dont la composante dirigée verticalement est appelée la portance. C’est la portance… »
Nope, ceci n’est pas la raison de la portance (en tout cas pas pour un avion, où l’aile devrait avoir la forme d’un demi-œuf pour espérer commencer à décoller du sol avec le seul effet de dépression).
La bonne explication est là : http://lehollandaisvolant.net/?d=2011/01/15/22/46/21-comment-vole-un-avion
Si, si, c’est bien la raison de la portance :-p
Relisez bien la phrase que j’ai écrite, et que vous citez entre guillemets. Elle est parfaitement correcte et c’est bien la vitesse supérieure qui provoque une dépression qui entraine la portance.
Ce qui est en revanche incorrect, et que je n’ai PAS dit, c’est l’explication (fausse) du « temps de transit égal », qui est celle qu’on entend parfois et que j’ai mentionné dans mon dernier paragraphe. C’est également cette explication qui est critiquée dans les liens que vous mentionnez à la fin de votre billet (comme ici http://www.grc.nasa.gov/WWW/K-12/airplane/wrong1.html ou là http://www.allstar.fiu.edu/aero/airflylvl3.htm)
Mais l’explication « différentiel de vitesse » => dépression est tout à fait correcte. Ce qui est incorrect, c’est d’expliquer le différentiel de vitesse par la longueur du chemin à parcourir (et qui effectivement nécessiterait des ailes démentielles).
Quant à la théorie de la déviation du flux d’air, elle est correcte, mais pas du tout incompatible avec celle de l’effet Bernoulli ! Ce sont deux manière différentes de regarder le même problème !
Prenons un autre exemple : c’est comme si on considérait le fait qu’une balle lancée à la verticale finit par freiner. Si je dis « c’est à cause de la force de gravité », et que vous dites « c’est à cause de la conservation de l’énergie », nous avons tout les deux raison. L’explication « force » est plus « proximale », alors que l’explication « conservation de l’énergie » est plus « téléologique ». Mais elles se déduisent l’une de l’autre.
L’explication « déviation du flux d’air / 3eme loi » est typiquement téléologique, mais n’explique pas le détail du mécanisme. Je préfère personnellement Bernoulli.
A noter aussi que l’explication « déviation du flux d’air » s’appliquerait aussi pour la théorie balistique (fausse pour les avions classiques), et nécessite dans tous les cas de faire le calcul du flux d’air dévié, et donc de retomber sur Bernoulli.
Tiens au passage, je me demande si la théorie balistique est correcte pour les avions en papier. j’ai envie de penser que oui…
Pingback: Comment les insectes font-ils pour voler ? | My...
Ça c’est un beau papier (et je ne manquerai pas de le relire), ça me fait penser à deux choses, comme ça, en passant : que le Colibri (http://fr.wikipedia.org/wiki/Colibri) est bien un phénomène (avec ses vols stationnaires), et que ce mouvement d’aile de l’insecte ressemble à s’y méprendre au mouvement de la « godille » en bateau (http://fr.wikipedia.org/wiki/Godille)… Pour l’histoire du temps de parcours, arf ! tu m’as tué.
Je veux bien croire le bon Dr Goulu quand il m’explique que le ressenti et la compréhension instinctive ont leurs limites pour l’abord des phénomènes physiques, et j’applaudis aussi à la classe de vos articles, tout en finesse technique et laissant apprécier un humour cependant toujours sérieux (!), MAIS je n’ai toujours pas trouvé de réponse à ma question pourtant primaire :
Si la portance est effectivement provoquée par le théorème de Bernoulli (dépression au dessus) et non celui de Newton (pression en dessous), voire même par la différence pression/dépression de ces deux piliers de l’aéronautique enfin réconciliés,
comment se fait-il que lorsqu’on tend sa main à la fenêtre d’une voiture, on sent distinctement la pression de l’air la soulever et non pas la dépression de l’air l’aspirer ?
(et ceci quelle que soit la position de la main, ce je précise pour les esprits contradicteurs très forts en déni de l’évidence à des fins de décrédibilisation scientifique ou non, qui m’ont déjà répondu que c’était dû à la différence de sensibilité entre la paume et le dessus de la main, si, si…)
Une piste de réponse ?
Une nouvelle piste de recherche pour un nouvel article approfondissant la question ?
(dites ‘oui’, Ô s’il vous plaît, dites ‘oui’ ! O:-) )
Attention, soyons clairs : il n’y a pas d’explication universellement juste ou fausse. Il faut avoir en tête que suivant le problème précis dont on parle, un ou plusieurs mécanismes peuvent être à l’oeuvre, et certains dominants sur d’autres.
La théorie de la « pression par en-dessous » prédit une portance dont l’intensité varie comme $latex sin^2 \alpha$ (l’angle d’attaque) alors qu’avec l’explication « dépression » on a généralement une dépendance en $latex \sin\alpha$. Ca ne veut pas dire que la « pression par en-dessous » n’existe pas ! Juste que son intensité n’explique pas à elle-seule la manière dont volent les avions usuels (ou dont avancent les voiliers, parfois « contre le vent »).
Par exemple, je ne serai pas surpris que les avions en papier trouvent leur portance uniquement dans « la pression par en-dessous ». Peut-être cette question fera-t-elle l’objet d’un article 😉
« Peut-être cette question fera-t-elle l’objet d’un article » : voilà ! 😀 😉
La base pour aborder le topic : posséder soi-même une connaissance claire de la chose , puis être capable de l’ exprimer simplement . Vous ne semblez pas imprimer que vous demandez là le maximum , une capacité très rare.
Contrairement à l’ idée populaire , seuls ceux qui dominent de haut , tout le domaine , sont capables de cette perfo appelée » vulgarisation » = expliquer une réalité parfaitement cohérente du domaine ( qui en aura autant que de profs ayant acquis cette domination ) . Et seuls ceux qui savent exprimer simplement cette connaissance , peuvent être reçus par leur entourage !.
Les » ceux » appartenant à l’ inter de ces deux ensembles décrits , sont rares , et admirables .
Cette capacité à vulgariser étant le plus élevé des états de la connaissance : celui qui traduit la capacité de connexité de ce savoir là, avec tous les autres, permettant alors un choix d’images didactiques assez efficaces pour toucher le néophyte aspirant à comprendre . Et cet athlète complet ne court ni les forums ni les couloirs des studios télé !
A reblogué ceci sur Digital Curiosities.
Pour David dans le « pour aller plus loin » vous écrivez : « Pour changer de direction en situation normale, les insectes utilisent le phénomène du lacet : une rotation autour de l’axe vertical. C’est ce que font les avions quand ils agissent sur la gouverne de direction. »
C’est ce que ne font pas les avions en situation normale : quand on est dans un Airbus ou un Boeing en approche autour d’une ville pour atteindre un aéroport, on remarque que l’avion se penche selon un axe longitudinal (roulis). Ce n’est pas pour que les passagers puissent admirer le sol (mais j’aime beaucoup ce spectacle), c’est pour tourner. Un virage normal met simultanément en jeu le palonnier et le manche. Un virage en lacet seulement n’est pas une situation normale.
Merci de ces articles passionnants.
Wow! Vraiment un excellent article sur le sujet. Ayant déjà réalisé plusieurs maquettes d’avions en balsa, le vol des moustiques m’a toujours intrigué mais je n’avais jamais pris le temps de lire à ce sujet. Merci pour l’explication.
C’est complétement stupide de faire des comparaisons et essayer de comprendre le vol des insectes en fonction des petites connaissances de l’homme à ce sujet .
Il n’y a aucun point commun avec la portance et tout le bla bla bla d’aérodynamicien et la mécanique du vol des insectes .
Dikinson de Berkeley n’ a jamais réalisé et compris réellement le vol de la mouche .
Les millions de $ versé par la Navy pour les recherches ne servent à rien .
Les secrets sont toujours bien gardés .
Ce n’est pas demain la veille qu’un drone vas voler sur le principe du battement d’aile de mouche .
Il faudra attendre la publication de mon livre que j’ai commencé en 2006 pour comprendre réellement le vol de la mouche .
Les ecrets sont dans mon livre .
Il y a déjà 50 page de réalisées , il me reste encore 50 page à écrire .
On attend avec impatience que vous nous éclairiez de votre auguste sapience !
I ]
Il y a autant de façon d’expliquer le vol que de profs possédant bien leur domaine ! Parmi celles qui fonctionnent , il en est une , + proche de l’ origine newtonienne = celle des quantités de mouvement .
On ne parle plus de » pression » , mais de déflexion et de masses mises en vitesse .
Le profil , ou la gouverne dans le flux , dévie une masse d’ air (Fr . dt = ß . dM/dt ), qui par réaction
(Fr ),induit une force de direction opposée à la vitesse ( barycentrique ) de sortie de la masse d’ air déviée .
L’équation des forces de Newton , doit juste tenir compte de la viscosité en ajoutant un terme en ( – k V )
et elle peut alors gérer aussi bien le vol d’un oiseau , d’une planche à prof autostable que celui de l’ insecte . Il n’ y a plus de paradoxes ni de magie .
Cette vision simplifiée induit d’ailleurs la même expérimentation .
Seule la valeur des coeff ( K / visco = f( visco dynamique, temp, écoulement ) et ß = 1/2 .Ro, Re ( pour les rendements aéro ) va déterminer le type de force générée par le mouvement relatif .
F = ß . dM/dt – K S V
( F , dM/dt et V = grandeur vectorielles )
L’ aérodyn, étude des forces d’origine Aéro , revient alors à celle de la déviation du flux .( par profil , aile battante, tournante ..,delta de pression dans tuyère et jet de masse fluide…).
EXEMPLE APPLI =
Pour 1 Rotor hélico p ex :
Equil : force réaction à masse air ejecté vers le bas avec poids .
Mg = M delta V = densité x volume x delta V = r° x S rot x V x V = r°SV²
r° : masse volumik . S = surf rotor . V moyenne des vitesses air sortie de rotor .
II ]
Autre sujet : Léonard de Vinci .
On démontre assez facilement que Léonard ne peut pas avoir été l’ inventeur de ces formes aéro ( aile ) , autres objets devant planer , et autres découvertes référencées dans ses écrits ..
Il ne disposait ni des outils de Newton,ni des moyens de calcul dus à Pascal & Descartes pour les prévoir par génie conceptuel et calcul.
Il devait donc recourir à la gamberge , (inventivité instinctive ) , à l’ expérimentation récurrente en boucle pour parvenir par itération au dessin et réglages enfin efficace . ( Profil auto-stable et approche des Pb de proxi relative foyer /C de G ).
Un process demandant une trentaine d’ année ( étude, conception , fabric , réglages ), à toute époque de l’ Humanité !
On en connait deux ayant abouti au vol réel dans ce lap de temps :
– Ibn Firman , Maitre Université de Cordoue vers l’ an 760 ,
– les frères Lillienthal , Allemagne centrale vers 1893 .
A 1100 ans de distance , on retrouve les mêmes moyens : étude du vol des oiseaux , empirisme de haute qualité, et les mêmes matériaux = soie , bambou , colles & ligatures . Et une solide santé & bonne résistance aux chocs pour expérimentateur . ( Ibn Firman le paiera d’un jambe cassée (il a 60 ans !) et Otto Lillienthal de sa vie en 1996.
Chacune de ces trajectoires de progrès peut être virtuellement translatée dans le temps , sans en changer les donnés ni les chances de succès . N’importe quelle époque d’une paix suffisamment longue de l’ Histoire humaine aurait pu engendrer le vol humain . Seul le développement de la métallurgie a conditionné celui des moteurs.
Da Vinci peut juste être considéré comme un bon artiste vulgarisateur de ce domaine , peut être, pas trop soucieux d’ honnêteté quand à ses sources .
Octobre 2017, par hasard je repasse par là. Mon livre a actuellement 120 pages. Presque terminé.
Pour vous donner une petite idée du pourquoi du comment volent les insectes, il vous faut apprendre à manier une pagaie.
Et quand vous voyez une mouche, c’est avec deux pagaies quelle vole dans l’air. Quand vous pagayez dans l’eau, c’est un coup de pagaie et la mouche, c’est 200 à 450 coup de pagaies par seconde.
Pour établir des calculs, c’est simple, Il faut prendre en compte la différence de densité de l’air et de l’eau.
Antoine Magnan était mon grand père.
Donc il faut prendre les puissances de l’énergie de la pagaie X 250 et 450, et faire les différences de densité de l’eau et de l’air . Facile , Non ?
Pingback: Des hydrofoils de grande taille ? – Foilers !