C’est un grand classique, mais après ce que je vous ai infligé la semaine dernière, je me suis dit qu’un peu de repos ne ferait de mal à personne !
Donc nous allons démontrer que tous les triangles sont équilatéraux. Rien que ça !
Et puisqu’on démontre que tous les triangles sont équilatéraux, il s’ensuit que 1+1=3, que les maths sont contradictoires, que Gödel l’avait prédit et que je suis le pape.
La démonstration
Prenons un brave triangle ABC, et considérons deux éléments de ce triangle:
- La médiatrice du côté BC, c’est à dire la perpendiculaire qui sépare le segment BC en deux parties de même longueur;
- La bissectrice de l’angle A, c’est-à-dire la droite qui sépare l’angle A en deux angles égaux.
Le schéma ci-dessous montre ces deux éléments. Je vais noter P leur point d’intersection et D le milieu du segment BC.
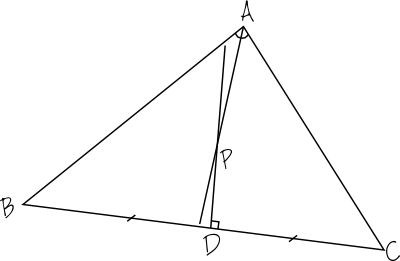 Notez que sur le schéma, j’ai fait figurer avec les petits symboles habituels que BD = DC et que l’angle A est coupé en deux angles égaux.
Notez que sur le schéma, j’ai fait figurer avec les petits symboles habituels que BD = DC et que l’angle A est coupé en deux angles égaux.
Je considère maintenant les perpendiculaires à AB et AC qui passent par P. J’appelle E et F les points selon le schéma ci-dessous.
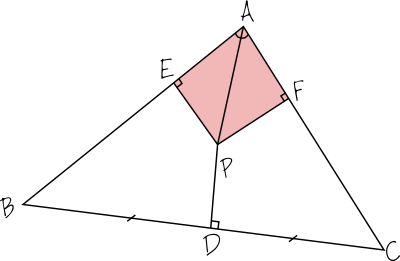 Je vais me concentrer sur les deux triangles représentés en rouge ci-dessus : AEP et AFP. Ce sont tous les deux des triangles rectangles (par construction), et qui ont un autre angle identique, l’angle au sommet qui est la moitié de l’angle A (rappelez-vous, AP est la bissectrice). Les deux triangles rouges ont donc leur trois angles identiques, et comme ils ont une hypoténuse commune, ils sont égaux ! En particulier AE = AF et PE=PF, je fais figurer cela sur le schéma ci-dessous.
Je vais me concentrer sur les deux triangles représentés en rouge ci-dessus : AEP et AFP. Ce sont tous les deux des triangles rectangles (par construction), et qui ont un autre angle identique, l’angle au sommet qui est la moitié de l’angle A (rappelez-vous, AP est la bissectrice). Les deux triangles rouges ont donc leur trois angles identiques, et comme ils ont une hypoténuse commune, ils sont égaux ! En particulier AE = AF et PE=PF, je fais figurer cela sur le schéma ci-dessous.
Maintenant je relie P à B et C, et je considère les deux triangles en jaune : PBD et PCD. Ce sont tous les deux des triangles rectangles, et ils ont deux côtés identiques : PD qui leur est commun, et BD=CD (rappelez vous que DP est la médiatrice au segment BC.) Par le théorème de Pythagore, on peut conclure que les deux triangles sont identiques. En particulier PB=PC, que je fais figurer sur le schéma.
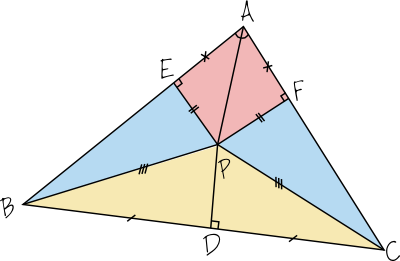 Considérons maintenant les triangles bleus ci-dessus PEB et PFC. Encore une fois ce sont des triangles rectangles (par construction des points E et F), et qui en vertu des étapes précédentes ont deux côtés communs PE=PF et PB=PC. Donc à nouveau (par exemple par Pythagore), ces triangles sont identiques, et en particulier BE=CF.
Considérons maintenant les triangles bleus ci-dessus PEB et PFC. Encore une fois ce sont des triangles rectangles (par construction des points E et F), et qui en vertu des étapes précédentes ont deux côtés communs PE=PF et PB=PC. Donc à nouveau (par exemple par Pythagore), ces triangles sont identiques, et en particulier BE=CF.
Nous venons à l’instant de démontrer que BE=CF et on avait précédemment EA = FA, donc on conclut que AB=AC. Donc le triangle ABC est isocèle. Et comme la démonstration que l’on vient de faire a été appliquée à l’angle A mais qu’on aurait pu tout autant l’appliquer en B ou en C, il est aussi équilatéral. Donc tous les triangles sont équilatéraux. CQFD.
(Et puisque demain c’est le 1er avril, je laisse au lecteur en exercice le soin de démontrer que je suis le pape.)
Règle du jeu :
- Si vous ne connaissez pas le truc, vous avez le droit de proposer votre solution en commentaire;
- Si vous connaissez le truc, laissez chercher les autres ! (Si vous donnez quand même la réponse en commentaire vous perdez 3 points de karma)
- Si vous ne connaissez pas le truc, que vous le cherchez sur Internet, et que vous postez la solution en faisant croire que vous l’avez trouvé tout seul, vous perdez DIX (10) points de karma !
Spéciale dédicace à mon papa, qui m’avait parlé le premier de cette démonstration, il y a bien longtemps !
(Edit du 31/03 : Finalement j’ai viré les préliminaires : c’était faux — merci aux commentateurs — et finalement plutôt inutile…)
Edit du 04 Avril : La solution !
Comme de nombreuses personnes l’ont remarqué en commentaire…il y a un problème avec le dessin ! Le point P devrait être à l’extérieur du triangle. Et voici la clé de l’énigme !
Ce qui fait pour moi tout l’intérêt de cette « fausse » démonstration, c’est qu’elle est en fait complètement correcte du début à la fin…sauf au tout dernier moment. Là où cela paraît le plus simple et le moins suspect !
Toutes les égalités démontrées ici sont vraies, et les triangles « identiques » le sont réellement. Là où l’on triche, c’est à la toute fin, quand de EB=FC et AE=AF (qui est correct) on déduit AE+EB= AF+FC (qui est correct) et donc AB=AC (qui est faux en général !). Si P est à l’extérieur, E (ou F) ne sera pas dans le segment AB (ou AC) et on n’a pas le droit d’additionner les longueurs de cette manière ! Donc si le dessin est mal fait, on se laisse avoir !
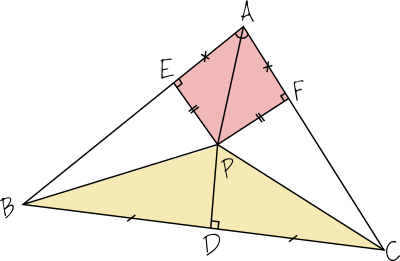
Ci-dessous un dessin fait correctement. J’ai pris un triangle clairement pas isocèle, et j’ai conservé les mêmes couleurs pour les triangles considérés (qui, je le répète, sont bien « identiques »). Comme ces triangles sont parfois superposés (contrairement à mon mauvais dessin initial) j’ai essayé de rendre en mélangeant les couleurs :
Les deux triangles rouges sont identiques, les deux bleus sont identiques, les deux jaunes sont identiques.
Une question que l’on peut se poser, c’est comment démontrer que P est toujours à l’extérieur ? Dans les commentaires, Nicolas a proposé une solution basée sur le théorème suivant, qui affirme que le point M où la bissectrice intersecte BC vérifie MB/MC = AB/AC. Comme me le faisait remarquer une lectrice (merci Marie !) une autre manière de le démontrer, c’est par l’absurde, en utilisant la démonstration de ce billet ! Si le point P est à l’intérieur, alors on aboutit à une contradiction…donc le point P est à l’extérieur !
Bravo à tous ceux qui ont trouvé la solution par eux-mêmes, ou qui s’en sont approchés !
Billets reliés
La plus belle démonstration du théorème de Pythagore
Crédits
Triangle, runmonty Flicker/CC
Schémas : Science étonnante






47 Comments
Vraiment super intéressant, j’avoue que je n’ais trouvé la solution (cherché sur internet) mais que cette anecdote m’a tout de même fait réfléchir un bon paquet de minutes :p
Merci 🙂
Bonsoir, c’est fascinant!
Je ne connaissais pas la réponse, mais j’y ai réfléchi, je pense avoir trouve.
La première chose que j’ai remarquée est que la médiatrice de [BC] n’est graphiquement pas correctement tracée…volontairement, je présume !
Je l’ai mentalement dessinée correctement et, sans surprise elle est quasiment confondue à la bissectrice en A (attendez)
Or, seuls les triangles isocèles en A (en reprenant les points utilises) voient leur bissectrice en A confondue avec la médiatrice du côté opposé
D’autre part, si on suit votre raisonnement (en rétablissement la médiatrice à sa place graphiquement!), cela n’amène qu’à une seule conclusion: le triangle est isocèle, ce qui est un pléonasme vu les conditions posées par votre dessin, rendant médiatrice et bissectrice confondues.
En effet, on ne peut conclure que le triangle est équilatéral car en appliquant le raisonnement à B, puisqu’ABC n’est isocèle qu’en A, on trouve que….la bissectrice depuis B ne coupe absolument pas le côté AC.
Morale de l’histoire : dans tout triangle , la médiatrice d’un segment coupe la bissectrice de l’angle opposé si et seulement si le triangle est isocèle.
Ai-je tort? Merci en tout cas pour ce petit exercice nocturne
ERRATUM corrections (merci de supprimer le précédent)
Bonsoir, c’est fascinant!
Je ne connaissais pas la réponse, mais j’y ai réfléchi, je pense avoir trouve.
La première chose que j’ai remarquée est que la médiatrice de [BC] n’est graphiquement pas correctement tracée…volontairement, je présume !
Je l’ai mentalement dessinée correctement et, sans surprise elle est quasiment confondue à la bissectrice en A (attendez)
Or, seuls les triangles isocèles en A (en reprenant les points utilises) voient leur bissectrice en A confondue avec la médiatrice du côté opposé
D’autre part, si on suit votre raisonnement (en rétablissement la médiatrice à sa place graphiquement!), cela n’amène qu’à une seule conclusion: le triangle est isocèle, ce qui est un pléonasme vu les conditions posées par votre dessin, rendant médiatrice et bissectrice confondues.
En effet, on ne peut conclure que le triangle est équilatéral car en appliquant le raisonnement à B, puisqu’ABC n’est isocèle qu’en A, on trouve que….la bissectrice depuis B ne coupe absolument pas la médiatrice de AC.
Morale de l’histoire : dans tout triangle , la médiatrice d’un côté coupe la bissectrice de l’angle opposé si et seulement si le triangle est isocèle.
Ai-je tort? Merci en tout cas pour ce petit exercice nocturne
Pingback: Tous les triangles sont équilatér...
Je suis un peu d’accord avec le commentaire précédent… Rien nous dit que les différentes médiatrices et bissectrices de tous les cotés et angles du triangle ABC se coupent en un point P à l’intérieur du triangle et donc cette démonstration ne peut être appliquée de la sorte pour tous les sommets du triangle ABC.
Je crois que j’ai trouvé : pour un triangle quelconque, l’intersection de la médiatrice et de la bissectrice se situe hors du triangle. Du coup tout le reste de la démonstration est fausse (le carré rouge sort du triangle , etc.).
Un petit essai sur Geogebra et la réponse saute aux yeux. Demain je fais le coup à mes élèves !!
Pingback: Tous les triangles sont équilatér...
Je bute sur les préliminaires. Par identique tu veux bien dire « de même longueur » pour les côté et « de même mesure » pour les angles ?
Si oui que penser du triangle suivant ABC avec A=(0,0), B=(10,1), C=(11,0)
et du triangle ABC’ avec A=(0,0), B=(10,1), C’=(9,0) ?
N’a-t-on pas deux côté égaux (longueur(AB)=longueur(AB) et longueur(BC)=longueur(BC’)) et un angle égal (angle(BAC) = angle(BAC’)) ?
Du coup je n’ai pas lu la suite, mais c’est mal parce que ça m’aurait peut-être permi de comprendre.
Entre-temps j’ai lu la suite. Je viens juste préciser que le problème dans la démonstration ne vient pas du problème que j’ai soulevé (dans le sens où on peut corriger facilement ce point).
SPOILER.
Le problème a déjà été essentiellement décrit plus haut. On peut être un plus snob et dire qu’il est plus précisément ici : « Nous venons à l’instant de démontrer que BE=CF et on avait précédemment EA = FA, donc on conclut que AB=AC ».
Pour David : tu ne veux pas nous en dire un peu plus sur l’âge à laquelle on t’a raconté cela et sur ce que tu en as pensé à l’époque ?
Oui c’est faux ! (en tout cas incomplet)
J’ai simplifié finalement…
Pour occuper ceux qui ont trouvé afin qu’ils ne dérangent pas leur camarades qui cherchent toujours, je propose l’autre grand classique: la démonstration de 1=2
x2 = x*x
-> x2= (x+x+x+…+x) x fois
-> si 2 termes sont égaux leurs dérivés sont égales
-> 2x=(1+1+1…+1) x fois
-> 2x=x
-> après simplification
-> 2=1
Si deux dérivées sont égales, leurs primitives ne le sont qu’à une constante près.
égalité des fonctions implique égalité des dérivées donc pas d’erreur à ce niveau.
Par contre le nb de termes de la somme est variable lui aussi dans le membre de droite. Il faut donc prendre en compte sa variation : on doit donc ajouter un « x » à droite. L’égalité est alors rétablie.
Merci
« J’en vois déjà qui froncent les sourcils, et qui se disent « Est-ce qu’il serait pas déjà en train d’essayer de m’enfumer, là ? ». Mais non, pas de piège pour l’instant. Essayez de vous convaincre de cela avant de continuer. »
Ben si, justement :
Cas 2 : un angle égal COMPRIS ENTRE deux côtés égaux
Cas 3 : un côté égal COMPRIS ENTRE deux angles égaux
Merci pour la correction ! Finalement j’ai enlevé les préliminaires et détaillé dans le texte. C’était plus simple comme ça…
Pour le cas 3, c’est bien n’importe quels angles et n’importe quel côté. (si deux angles sont identiques, comme la somme des angles vaut 180°, le troisième l’est aussi)
C’est quoi un angle égal ?
L’égalité est un vieux concept, remplacé maintenant par l’identité, mais je suis de la vielle école.
Non, la démonstration est exacte : tous les triangles sont équilatéraux. Et comme dans un triangle équilatéral, la bissectrice est confondue avec la médiatrice du côté opposé, elles ont une infinité de points d’intersection. Et comme ab absurdo sequitur quodlibet, je suis Dieu et David est mon Pape. CQFD
Par contre, pour la première partie de la démonstration, je sèche encore…
AD n’est pas une droite. ADC n’est pas un triangle car il 4 angles.
Excuses. Ma réponse n’a pas de rapport avec le problème
J’aime les triangles ♡♥
Cest quoi ces mathématiques 1+1=3, chez moi 1+1=2 😀
J’ai essayé sur quelques exemples et le points P est toujours à l’extérieur du triangle, les points E et F ne pouvant être quant à eux tous les deux en même temps sur les côtés du triangle. Par conséquent les égalités AE + EB = AB et AF + FC = AC ne sont pas vraies simultanément. Donc même si AE = AF et EB = FC, le triangle n’est pas équilatéral.
ENFIN!!!
ça fait une bonne demi-heure que je cherche !
Il n’y a évidemment aucune supercherie au niveau de la figure, mais bien au niveau de la démonstration.
Pour ceux qui ont trouvé des contre-exemples avec le point P en dehors du triangle, c’est vous qui avez un cas particulier, pas l’auteur ; vous avez un triangle avec un angle obtus, mais la (fausse) démonstration fonctionne toujours, si ce n’est qu’effectivement les points E et F sont en dehors du triangle et que pour retrouver AB == AC il faille faire une soustraction plutôt qu’une addition.
Pour trouver la faille, il ne faut pas non plus chercher du coté des théorèmes, ils sont tous bon et souvent avec des paramètres en plus bien que non nécessaire. Il faut regarder du coté des déductions. (Cherchez les phrases commençant par « En particulier […] »
Je n’ai pas tracé de figure, mais il me semble bien pourtant que (dès que le triangle est non isocèle en A) le point P est extérieur au triangle. Idée de la preuve : la bissectrice est l’ensemble des points qui sont à égale distance de (AB) et de (AC) ; dans le cas isocèle en A le point D est sur la bissectrice ; déformez le triangle en déplaçant A parallèlement à (AC), disons vers la droite avec l’orientation de la figure ; on peut alors se convaincre que D est plus près de (AB) que de (AC) ; l’intersection de la bissectrice avec (BC) est donc à droite de D ; de là on conclut il me semble.
Bien sûr, je n’ai vérifié aucun détail ! C’est faux ?
« parallèlement à (BC) » et non (AC)
Mea culpa, je ne devrais pas faire de math passée une certaine heure.
Tu as effectivement raison.
Je croyais avoir trouvé « AE = PF et PE=AF » au lieu de « AE = AF et PE = PF » .
Après avoir tracé de jolies figures, on n’a pas AE=AF et EB = FC. J’ai l’impression que l’embrouille se situe au niveau des triangles rectangles bleus et rouges, et donc de Pythagore : on a appris à l’école a2+b2=c2, mais pour que deux triangles aient tous leurs côtés de même longueurs, il fait qu’ils aient au moins deux côtés de même longueurs (Pour c=5, on peut avoir a=√20 et b=√5, ou a=√5 et b=√20. Donc a différent de b). Or, là il n’y a que l’hypoténuse. Ce qui me chiffonne ce sont les angles….
J’ai regardé la réponse pour pouvoir la proposer à mon prof demain, pour le premier Avril… je me disais bien que sur mes figures avec outils ça ne fonctionnait pas ! (Alors que sur les figures à main levée, AF n’était pas égale à AE, pareil pour EB et FC, mais P était bien mignon à l’intérieur du triangle…)
Morale de l’histoire : toujours tracer une figure de manière précise avant de commencer à résonner !!
Merci pour cette énigme, ça me permettra de faire plancher mon prof demain !
Ah c’est excellent ta devinette merci David, c’était pas facile de trouver!
En supposant que M est l’intersection de la bissectrice partant de A et de BC, on a l’égalité suivante: AB/AC=MB/MC. Autrement dit, si AB>AC alors MB>MC. De ce fait, P est toujours en dehors du triangle 😉
Joli! je ne connaissais pas et il m’a qd même fallu faire un schéma…
En gros, on fait une addition au lieu d’une soustraction.
Merci
« Les deux triangles rouges ont donc leur trois angles identiques, et comme ils ont une hypoténuse commune, ils sont égaux ! En particulier AE = AF et PE=PF »
Heu… C’est faux ça !
Non, c’est vrai, a moins que tu aurais un contre-exemple 😉
Dans certains cas, l’intersection de la médiatrice et de la bissectrice peut être en dehors du triangle, ce qui faussera toute la suite…
Et en particulier, pour un triangle équilatéral (si c’est le cas, puisqu’on veut le démontrer), la médiatrice n’est autre que la bissectrice (autrement dit : il existe une infinité de points d’intersection), ce qui ne permettra pas le raisonnement qui suit après.
… Ou comment démontrer que si dans un triangle la bissectrice d’un angle croise la médiatrice du côté oppose à l’intérieur du triangle, alors ce triangle est isocèle…
Il n’y a pas ici de paradoxe à proprement parler, c’est la manière de présenter la démonstration qui induit en erreur. Comme quoi même en maths, tout résultat est sujet à l’interprétation!! Attention donc aux argumentaires scientifiques détournes pour légitimer ce qui est injustifiable
Vu en cours de didactique des maths, j’avais bien aimé.
Je me demande comment a été « construite » cette fausse démonstration. Si c’était à dessein (dans le but même de construire une preuve fausse) ou si c’était vraiment quelqu’un qui s’est trompé.
Ravi d’avoir contribué 😉
Ceci prouverai (bien sûr, c’est faux) que tout triangle est isocèle, mais pas que tout triangle est équilatéral. En effet, si on part d’un triangle isocèle en A, on prouve qu’il est isocèle en A et rien d’autre. On ne peut donc pas dire « il suffit de faire de même pour les autres angles ». Mais, ce n’est sans doute pas aussi clair que je le prétends. Y a-t-il un logicien dans l’avion ?
Pingback: La rotondité de la Terre et les voiles des bateaux | Science étonnante
A la recherche de la démonstration :
» Prouver que le point P (figure) se situe sur le cercle circonscrit du triangle ABC. »
Merci
Si trois (3) points définissent un plan comme deux (2) points définissent une droite , ils ne déterminent qu’une portion de celui-ci de dimension deux (2) . C’est pourquoi 1+1 = 2=3
Ce qui nous conduit à 2+2 = 5 et à
1= 0
La même erreur de raisonnement partant de la pseudo egalité:
a = b conduit au même resultat erroné.
Mohwali Awamar
On sait bien que les triangles ne sont pas tous équilatéraux et qu’il faut donc trouver l’explication de l’erreur de raisonnement. Et pourquoi donc l’existence d’un point P et celle d’un triangle non isocèle soient compatibles? Le parallèle est à faire avec l’illusion que le polygone régulier inscrit et celui exinscrit à un un cercle finissent par se confondre en le cercle par passage à la limite. En réalité le passage à la limite qui implique le nombre Pi transforme le cercle en figure ouverte qu’est la droite euclidienne et le résultat fait qu’il n’y a ni intérieur ni extérieur.
Mohwali Awamar
On peut également montrer que le point P (parfois appelé pôle sud) est toujours sur le cercle circonscrit du triangle ABC, et est donc nécessairement à l’extérieur de celui-ci.
Merci pour ce billet, je ne connaissais pas cette fausse démonstration !
Sans regarder la solution, je vois déjà un problème avec un triangle isocèle (et en considérant la bissectrice partageant l’angle unique, et la médiatrice partageant la base) : dans ce cas particulier, la médiatrice et la bissectrice étant confondues, l’intersection n’est pas réduite à un point…
Il y a donc un problème sur l’existence même de ce point.