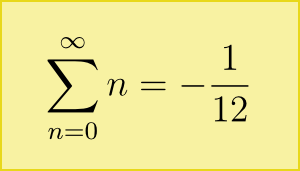Il y a quelques mois, j’ai écrit ce billet au sujet de la somme 1+2+3+4+5+… Toutes proportions gardées, ce billet est à ce jour le plus controversé de ce blog, et il m’a valu une flopée de commentaires parfois moqueurs ou condescendants.
Il faut dire que j’y expliquais que même si cette somme est a priori infinie, il est malgré tout possible de lui affecter une valeur finie : -1/12. Pire, on peut calculer cette valeur à partir de quelques manipulations heuristiques en apparence totalement interdites.
Absurde ! Ridicule ! Et pourtant les maths qui se cachent derrière ce résultat provocateur sont tout à fait réelles : bienvenue dans le monde des séries divergentes. Comme je n’en avais pas beaucoup raconté dans le premier billet sur les concepts mathématiques concernés, cela faisait quelques temps que je songeais à faire une suite un peu plus consistante à ce billet infamant.
Or il se trouve que Bruce, qui anime la chaîne YouTube « e-penser » a récemment rallumé le feu avec une vidéo présentant le même calcul. Quelques jours plus tard, le célèbre blog anglophone Bad Astronomy écrit également un billet sur ce calcul, et bien sûr c’est aussi l’indignation !
Timing parfait : j’ai décidé de m’y coller et d’expliquer vraiment de quoi il retourne. Nous allons donc voir pourquoi affecter la valeur -1/12 à la série 1+2+3+4+5+6+… n’est pas juste un canular d’un mec qui n’a rien compris aux maths, genre « je montre 1=0 en cachant une division par zéro dans le raisonnement ».
Affecter -1/12 à cette somme est possible sous certaines conditions, et les calculs heuristiques, quoique formellement faux, permettent étonnamment de retrouver cette valeur. Le pire : en physique on se sert de ce résultat en apparence absurde !
Petite mise en garde : En général, j’essaye dans mes billets de garder les connaissances nécessaires au niveau lycée. Aujourd’hui exceptionnellement, je vais taper un peu au-delà des maths du bac ! Si vous savez ce qu’est une série, ça peut aider…
Rappel des faits
Pour commencer, je voudrais rappeler les quelques petits calculs qui ont ému tant de monde. Oui, je sais, ces calculs sont a priori illicites, mais c’est précisément l’objectif de ce billet d’expliquer pourquoi ils ne le sont pas tant que ça. Alors ne partez pas au milieu !
Considérons la somme
\(A = 1-1+1-1+1-1+…\)
A priori cette somme n’a pas de valeur bien définie. Essayons quand même de lui en donner une ! Pour cela, on peut noter que
\(\begin{array}{rcl} A &=& 1-1+1-1+1-1+…\\ &=& 1 – (1-1+1-1+1-1+…) \\ &=& 1-A \end{array}\)
Puisqu’on a A = 1-A, on peut déduire que A=1/2.
Passons maintenant à plus ambitieux, la somme
\(B = 1-2+3-4+5-6+… \)
Même remarque, cette somme n’a en principe pas de valeur. Mais cette fois remarquons qu’on peut écrire
\(\begin{array}{rcl} B &=& 1-(2-3+4-5+6-7+…) \\ &=&1-(1-2+3-4+5-6+…)-(1-1+1-1+1-…) \\ &=& 1-B-A\end{array}\)
On a donc 2B = 1-A, et puisqu’on connaît la valeur de A, on peut en déduire B =1/4.
Le gros morceau maintenant, on considère la bête immonde, la somme
\(S = 1+2+3+4+5+6+… \)
On va cette fois soustraire B à S et obtenir :
\(\begin{array}{rcl} S-B &=& (1+2+3+4+5+…)-(1-2+3-4+5-…) \\ &=&(4+8+12+16+…)=4S\end{array}\)
donc S = B + 4S qui nous amène à la conclusion que S=-1/12.
Stop ! Arrêtez de hurler, je sais que tout cela est absurde ! Je manipule des objets non-définis, les séries divergent, et je prétend qu’une somme de termes positifs peut être négative, etc. Du délire total, quoi !
Et pourtant, on peut donner un sens précis et rigoureux à tout ceci. Alors voyons comment !
Comment sommer un nombre infini de termes ?
Commençons à la base : l’addition des nombres réels. Si je vous demande d’additionner deux nombres, vous savez faire. Si je vous demande d’additionner 3 nombres, vous allez me dire : pareil ! Et pourtant…
Ca vous paraît peut-être naturel d’écrire et de calculer 1+2+3, mais ça n’est pas si immédiat ! Notez que pour avoir le droit de l’écrire de cette manière, sans parenthèses, il faut invoquer l’associativité de l’addition, c’est-à-dire que (1+2)+3 = 1+(2+3). Rappelez vous : l’addition n’est au départ définie que pour 2 nombres, et c’est parce qu’elle est associative qu’on peut l’étendre à une somme de plusieurs nombres en oubliant les parenthèses.
Considérons maintenant une somme d’un nombre infini de termes, par exemple
\(1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + …\)
Comment faites-vous pour calculer cette somme ? « On prend le premier terme, on ajoute le second, puis le troisième, et ainsi de suite jusqu’au bout. » Ca vous paraît évident ? Et pourtant ça ne l’est pas !
Il y a quelque chose d’absolument critique à comprendre : RIEN dans la définition usuelle de l’addition ne nous dit comment on peut sommer un nombre infini de termes. Cette somme est donc a priori un objet indéfini.
Pour lui affecter une valeur, il faut dire comment on fait. Ça n’est pas neutre, car cela signifie qu’il faut faire un choix. On dit que l’on va définir une méthode de sommation. C’est un point très important à saisir car tout le reste repose là-dessus.
La méthode de sommation la plus naturelle, c’est de prendre la limite de la suite des sommes partielles. Histoire d’être précis, je vais faire un peu de formalisme.
La méthode « naturelle »
On considère une suite \(a_n\) de nombres réels (pour simplifier), et on cherche à affecter à cette suite un nombre réel, que l’on veut associer intuitivement à la somme de tous les \(a_n\). On veut donc construire une application (notons-là \(\Sigma\)), à valeur dans \(\mathbb{R}\), et définie sur l’espace vectoriel des suites réelles (enfin au moins un sous-espace vectoriel) .
La manière naturelle de définir \(\Sigma\), c’est de considérer la suite des sommes partielles
\(S_n = a_0 + a_1 + a_2 + … + a_n\),
et de calculer sa limite quand \(n\) tend vers l’infini. Si cette limite existe et est finie, on dit que la série converge, et la limite est considérée comme étant « la valeur » de \(\Sigma a_n\) :
\(\Sigma a_n \equiv\mathrm{lim}_{n\to\infty} (a_0 + a_1 + a_2 + … + a_n) \)
Voilà, j’ai décrit mon application \(\Sigma\), et elle est définie sur un sous-ensemble de l’espace des suites réelles: celui pour lesquelles la limite de la suite des sommes partielles existe (notons le \({\cal C}\))
Je me répète : prendre la limite de la suite des sommes partielles est la manière la plus naturelle de faire, celle que l’on fait quand on dit « on prend le premier terme, on ajoute le second et ainsi de suite », mais il s’agit d’une définition, d’un choix. Cette procédure ne découle pas « automatiquement » de l’addition usuelle.
Pour vous convaincre qu’il s’agit d’une extension de l’addition usuelle, en voici une conséquence étonnante : quand on a une somme d’un nombre infini de termes, la valeur de la somme peut dépendre de l’ordre des termes !
Bye bye la commutativité !
Vous le savez, quand on fait des additions, l’ordre ne compte pas : 1+2+3 = 3+1+2, par exemple. C’est une autre propriété de l’addition qui s’appelle la commutativité. C’est bien pratique, mais pour les sommes infinies, ça ne marche pas toujours !
Considérez par exemple cette somme, que l’on appelle la série harmonique alternée
\(H = 1 – 1/2 + 1/3 – 1/4 + 1/5 – 1/6 + … \)
c’est-à-dire la série de terme \(a_n=(-1)^{n-1}/n\). On peut assez facilement montrer que la limite de la suite des sommes partielles vaut \(ln(2)\). On a donc envie de dire qu’il s’agit là de LA valeur de cette somme infinie.
Et pourtant, si on change l’ordre des termes dans l’addition, on peut changer la valeur de la limite. Plus fort encore, on peut montrer qu’on peut toujours changer l’ordre des termes pour la faire converger vers ce qu’on veut !
Oui oui, vous lisez bien. Si vous réarrangez comme il faut les termes de cette série, vous pouvez la faire converger vers \(\sqrt{42}/(e+\pi)\) si ça vous amuse. Et pire encore, ce résultat bizarre n’est pas du tout spécifique à cette série : il marche avec tout un tas d’autres !
(Pour ceux qui font des maths post-bac : ça marche pour toutes les séries convergentes mais pas absolument convergentes. Ça n’est pas très difficile à démontrer, c’est une preuve constructive de la permutation, et cela porte le nom de théorème de réarrangement de Riemann.)
Vous voyez donc que la définition « naturelle » d’une somme d’un nombre infini de termes est quand même loin d’être innocente, puisqu’on y perd une propriété fondamentale de l’addition : la commutativité !
D’autres méthodes de sommation ?
J’espère vous avoir convaincu que la méthode « usuelle » pour sommer des séries, d’une part est bien une définition (et donc résulte d’un choix); d’autre part n’est pas si gratuite que ça.
Clairement les trois séries que j’ai présenté au début (A, B et S) ne sont pas sommables par la méthode usuelle : leurs suites des sommes partielles ne convergent pas. On ne peut donc pas leur affecter un nombre fini par la méthode naturelle. Mais pourrait-on faire autrement ? Existe-t-il d’autres méthodes de sommation que la méthode « naturelle » ?
Je vous ai dit qu’on peut voir une méthode de sommation comme une application définie sur un sous-espace de l’espace vectoriel des suites réelles, et à valeur dans \(\mathbb{R}\). Évidemment, on ne veut pas faire n’importe quoi, alors on va poser quelques conditions pour dire ce qu’est une méthode de sommation raisonnable.
La principale, c’est qu’on aimerait trouver une méthode qui soit compatible avec la limite de la suite des sommes partielles. On n’a pas envie de construire une méthode qui se mette à affecter de nouvelles valeurs aux séries convergentes ! En pratique, on cherche donc une application \(\tilde{\Sigma}\) qui soit un prolongement de l’application \(\Sigma\), c’est-à-dire :
- qui soit définie sur un espace plus large que l’espace \({\cal C}\) de définition de \(\Sigma\);
- qui coïncide avec \(\Sigma\) sur \({\cal C}\).
La méthode de Cesaro
Une de ces méthodes, c’est la méthode dite de Cesaro. Au lieu de prendre la limite de la suite des sommes partielles, on prend la limite de la moyenne des sommes partielles, c’est-à-dire qu’on définit
\({\Sigma^C}\ a_n\equiv\mathrm{lim}_{n\to\infty}\frac{1}{n}(S_0+S_1+S_2+…+S_n)\).
J’ai appelé cette application \({\Sigma^C}\) pour la distinguer de la méthode usuelle. Je vous laisse vous convaincre que cette méthode est bien un prolongement de \(\Sigma\) : elle est définie plus largement, mais pour toute série convergente, on retrouve le même résultat que la méthode usuelle.
Que nous apporte cette nouvelle méthode ? Prenez la série que je notais A au début de ce billet (qu’on appelle la série de Grandi, et qui n’est pas sommable par la méthode usuelle) la méthode de Cesaro permet de lui affecter une valeur, et cette valeur est 1/2 ! Tiens, la même valeur que celle que l’on trouve avec les manipulations initiales…
La méthode d’Abel
Voyons une autre méthode un peu plus générique, qu’on appelle la méthode d’Abel. L’idée est de considérer la fonction définie par la série entière
\(f(x) = \sum a_n x^n\),
et de voir si elle possède une limite quand x tend vers 1, ce qui formellement représente la somme \(a_0+a_1+a_2+…\). Posons donc la définition de cette méthode de sommation, et appelons là \(\Sigma^A\) :
\({\Sigma^A}\ a_n\equiv\mathrm{lim}_{x\to 1} \sum a_n x^n \).
Voyons ce que ça donne avec la série que je notais B au début du billet. On définit la fonction
\(f(x)=\sum (-1)^{n-1} n x^n = -x \sum (-1)^n n x^{n-1}\)
Si vous êtes habitués à dériver des séries entières, je vous laisse vous convaincre qu’on a
\(f(x) = -x \frac{d}{dx}\left(\frac{1}{1+x}\right) = \frac{x}{(1+x)^2}\).
Or vous voyez que cette fonction se trouve bien définie pour x=1, et vaut 1/4…la même valeur que le calcul heuristique effectué sur B !
Alors est-ce que les calculs du début de ce billet seraient quand même justes ?
Stabilité, linéarité, régularité
Non, « stabilité, linéarité, régularité », ça n’est pas une nouvelle devise pour le pays. Il s’agit de trois propriétés importantes que vérifient les deux méthodes de sommation que j’ai présentées ci-dessus :
La régularité, c’est le fait qu’une méthode coïncide avec la méthode usuelle sur les sous-espaces où elles sont toutes les deux définies. Nous en avons parlé.
La linéarité, c’est le fait que l’opérateur de sommation soit linéaire dans l’espace vectoriel des suites, c’est-à-dire que si on attribue la valeur A à la série de terme \(a_n\) et la valeur B à la série de terme \(b_n\), alors on attribue la valeur \(\lambda A +B\) à la série de terme \(\lambda a_n + b_n\), pour \(\lambda\) un scalaire.
La stabilité, c’est le fait que l’on puisse toujours sortir un nombre fini de termes en tête de la série, de sorte que
\(\Sigma a_n = (a_0 + a_1 + … + a_K) + \Sigma a_{n+K}\)
Maintenant, reprenez les calculs du début de ce billet. Si vous les observez attentivement, vous observerez qu’ils ne se basent que sur ces 3 propriétés !
Cela signifie que si on suppose qu’il existe une méthode de sommation stable, linéaire et régulière permettant de sommer la série, alors ces calculs sont valides et conduisent à la bonne valeur !
Pour vous le prouver, je vais récrire le premier calcul de manière tout à fait licite. Supposons qu’une méthode de sommation \(\tilde{\Sigma}\) existe pour la suite (1,-1,1,-1,1,…), et que cette méthode soit stable, linéaire et régulière.
Alors on a :
\(\begin{array}{rclr}A &=& \tilde{\Sigma}(1,-1,1,-1,…)\\ &=&1+\tilde{\Sigma}(-1,1,-1,+1,…)&\mathrm{Stabilite} \\&=&1-\tilde{\Sigma}(1,-1,1,-1,…)&\mathrm{Linearite} \\ &=&1-A&\end{array}\)
Vous voyez donc que le calcul heuristique sur A mené au début de ce billet est parfaitement légal, pour peu que l’on sache exactement ce qu’on fait ! Et on n’a le droit de n’utiliser que la stabilité et la linéarité. Notamment toute opération de reparenthèsage est interdite, ou toute modification de l’ordre des termes de la série. Ces manipulations en apparence innocentes sont interdites si on veut que les calculs « heuristiques » donnent un résultat sensé. Et bien sûr, ces calculs ne sont licites que si on sait par avance qu’une méthode de sommation stable et linéaire existe pour la série que l’on regarde. Mais si une telle méthode existe, alors le calcul heuristique est licite, et il donne la bonne réponse !
(Je laisse en exercice au lecteur de montrer que le calcul heuristique de B est valide lui-aussi. Attention à bien utiliser la linéarité : on n’a le droit que de sommer terme à terme !)
La régularisation par la fonction zeta
Un cas que je n’ai pas encore traité, c’est celui de la somme 1+2+3+4+5…Pour cette série, les méthodes d’Abel ou de Cesaro ne fonctionnent pas. Mais pour autant il existe une méthode de sommation qui fonctionne ! Pour une série de germe général \(a_n\), on définit
\(f(s) = \sum \frac{a_n}{n^{s+1}}\),
et on cherche si cette fonction (définie dans le plan complexe) admet une valeur ou un prolongement analytique en \(s=-1\). Pour la série 1+2+3+4+5+…, avec \(a_n=n\) on obtient la fameuse fonction dite « zeta » de Riemann. Cette fonction est définie de la manière suivante
\(\zeta(s) = \sum \frac{1}{n^s}\).
Or cette fonction admet bien un prolongement analytique en \(s=-1\), c’est-à-dire que formellement elle attribue une valeur à la série divergente \(\sum n\) ! Or il se trouve que ce prolongement analytique \(\zeta(-1)\) a pour valeur -1/12, comme pour le calcul heuristique !
Il existe une autre méthode de sommation, dite de Ramanujan, qui par une procédure différente associe aussi la valeur -1/12 à cette série divergente (voir ici). Vous voyez donc qu’il existe plusieurs méthodes de sommation bien définies qui affectent cette valeur à la série \(\sum n\). Si l’on sait de quoi on parle, tout cela est donc bien raisonnable !
Et pourtant, tout n’est pas clair pour autant, en tout cas pour moi !
Quelques questions ouvertes (pour moi)
A ce stade, on a envie de dire que la méthode de la fonction \(\zeta\) et la méthode de Rammanujan justifient le calcul heuristique de 1+2+3+4+5+…=-1/12.
Et pourtant il y a un hic. Dans le billet précédent, un généreux commentateur (nommé « Matheux ») m’a pointé le calcul suivant. Supposons qu’il existe effectivement une méthode de sommation \(\tilde{\Sigma}\) régulière, stable et linéaire définie pour (1,2,3,4,5,…), et qui lui assigne la valeur S, on a alors par stabilité :
\(\begin{array}{rclr} S &=& \tilde{\Sigma}(1,2,3,4,5,…) & \\ S &=& \tilde{\Sigma}(0,1,2,3,4,…) \\ S &=& \tilde{\Sigma}(0,0,1,2,3,…) \end{array}\)
Mais en additionnant la première ligne, la troisième et -2 fois la seconde (linéarité), on trouve
\(0=\tilde{\Sigma}(1,0,0,0,0,…)=1\)
Ce qui est contradictoire !
Ce calcul montre donc qu’il ne peut pas exister de méthode régulière, stable et linéaire qui soit définie pour 1+2+3+4+5+…(perso je n’ai vu écrit ce résultat nulle part ailleurs) En particulier les méthodes de Ramanujan et de la fonction zeta ne peuvent donc pas vérifier ces 3 conditions. Laquelle n’est pas satisfaite ? Je n’en suis pas sûr, mais je pense que c’est la linéarité. (Quelqu’un a une idée ?)
Est-ce à dire qu’il n’existe pas de manière unique d’assigner une valeur à cette série divergente ? Pourtant il est fascinant de voir que la méthode de la fonction \(\zeta\), la méthode de Ramanujan et la méthode heuristique trouvent toutes la même valeur ! (Au passage, dans mon calcul heuristique, je viole une des 3 conditions, saurez-vous retrouver laquelle et où ?)
Peut-on d’une manière ou d’une autre dire que cette valeur est unique ? Ou qu’elle correspond à un groupe d’hypothèses bien définies ? Ca serait bien, car comme je l’expliquais dans mon premier billet, la valeur de -1/12 est utilisée dans quelques modèles de physique théorique, et notamment c’est elle qui détermine les fameuses dimensions supérieures de la théorie des cordes.
Une piste pour cela, si on voulait appliquer la méthode d’Abel à la série 1+2+3+4+…, il faudrait définir
\(f(x)=\sum n x^n=\frac{x}{(1-x)^2}\)
Cette fonction n’admet pas de prolongement en x=1 (Abel ne marche donc pas), mais si on pose \(x=e^{-h}\), on obtient en \(h \to 0\) :
\(\frac{1}{h^2} – \frac{1}{12} + \frac{h^2}{240} + …\)
On voit qu’une fois ôté le terme singulier inital, on retombe sur -1/12 en h=0 c’est-à-dire x=1. Ca doit plus ou moins correspondre à ce qui se passe avec la formule de MacLaurin (voir mon billet précédent)
\(\sum_n f(n) – \int_0^{+\infty} f(x) dx = \frac{1}{2} f(0) – \frac{1}{12} f'(0) + …\)
qui quand on l’applique (illégalement) à la fonction \(f(x)=x\) donne :
\(\left(\sum_n n – \int x\ dx\right) = – 1/12 \)
On retombe sur le -1/12, et la soustraction de l’intégrale à la somme doit physiquement bien correspondre à ce qu’on fait en théorie quantique des champs pour se débarrasser des infinis dus aux énergies de point zéro. Donc les méthodes de Rammanujan ou de zeta sont certainement physiquement justifiables !
En conclusion :
- Il est possible d’affecter formellement des valeurs à certaines séries divergentes sous certaines conditions
- Ceci produit des méthodes mathématiques utiles pour aborder certains problèmes physiques.
N’est-ce pas tout ce qu’on demande aux maths ?
Si vous êtes arrivés jusqu’ici, bravo ! En tout cas vous voici maintenant du côté obscur, car Abel lui-même disait en 1826:
Les séries divergentes sont une invention du diable et c’est une honte qu’on ose fonder sur elles la moindre démonstration. On peut tirer d’elles tout ce qu’on veut quand on les emploie et ce sont elles qui ont produit tant d’échecs et tant de paradoxes. (…) Mes amis, voici quelque chose dont il faut se moquer.
Quelques références en vrac :
- Un excellent billet de Terence Tao qui donne des réponses à plusieurs questions qui se posent à la fin de ce billet : pourquoi la méthode zeta n’est pas stable, quelle est la connection avec Euler-McLaurin, etc. Ca picote un peu, mais il est fort le bougre ! (merci Hervé !)
- L’article Wikipédia Divergent Series
- La bible du sujet, Divergent Series de Hardy
- Un très bon billet en anglais The surprising flavor of Infinite Series, que Lê a écrit après avoir lu et commenté mon premier billet, et où il compare fort opportunément la sommation des séries divergentes à la préparation du fugu !
239 Comments
Pingback: 1+2+3+4+5+6+7+… = -1/12 ! | Science étonnante
la stabilité suppose que l’on puisse retirer des termes d’une suite, pas d’en ajouter. Donc pour votre « question ouverte », la suite que ‘on regarde c’est (0, 0, 1, 2, 3…). Les termes de la série de la fonction zéta ne sont pas déterminé pour zéro. La suite n’a donc pas de méthode de de somation.
Inversement les calculs que vous décrivez et qui conduisent a 0 = 1 prouvent par l’absurde que la suite en question (celle qui commence par les deux zéro) n’a pas de méthode de somation stable, linéaire et régulière.
A noter que si on regarde la série (a, b, 1, 2, 3…) avec a et b non nul. la série a bien sa méthode de somation et le petit calcul fait plus haut où on sort les deux premiers termes conduit à 0 = 0. Donc pas de problème.
Et encore merci pour ce blog.
La méthode heuristique utilise une autre propriété que régularité, linéarité et stabilité.
Reprenons la fin de la démonstration :
S – B = (1 + 2 + 3 + 4 + 5 + 6 + 7 + … ) – (1 – 2 + 3 – 4 + 5 – 6 + 7 + …) = (0 + 4 + 0 + 8 + 0 + 12 + 0 + …)
A ce stade de la démonstration, ilretire les 0 de la somme, alors que ni la régularité, ni la linéarité, ni la stabilité ne le permettent.
Ce retrait de 0 peut sembler anodin ; cependant, si nous reprenons les moyennes de Césaro et que nous considérons la somme suivante :
A’ = 1 + 0 – 1 + 1 + 0 – 1 + 1 + 0 – 1 + …
Je n’ai fait qu’ajouter des 0 dans la somme A ; et pourtant, il est facile de se convaincre que la somme en moyenne de Césaro vaut 2/3 et non 1/2.
Vous avez raison, Césaro ne permet pas de sommer les séries de cette façon. Il faut faire appel à Abel, puis à Dirichlet. La ligne qui vous perturbe, notamment, doit être effectuée avec la représentation en série de Dirichlet :
Considérons la série S-B = 0 + 4 + 0 + 8 + 0 + 12 + …
La série de Dirichlet associée est : 0/1^s + 4/2^s + 0/3^s + 8/4^s + 0/5^s + 12/6^s + … = 4/2^s + 8/4^s + 12/6^s + …
En mettant 4/2^s en facteur, on obtient : 4/2^s * (1/1^s + 2/2^s + 3/3^s + …)
On retrouve en facteur de droite la série de Dirichlet associée à 1 + 2 + 3 + 4 + 5 + …
De là, on peut finalement écrire que S-B=4S
Bonjour,
Dans votre premier billet vous donnez une autre definition (qui a l’avantage d’etre naturellement lineaire) de la regularisation par la fonction zeta. Celle que vous donnez ici pose des problemes de definition s’il y a des termes nuls.
Quoiqu’il en soit je crois que la stabilité pose probleme:avec la methode du precedent billet,on peut regulariser la serie de terme constant egal a 1, o.obtient la
On obtient la valeur de zeta(0), soit -1/2. Mais en rajoutant un zero devant, on obtient comme nouvelle valeur -3/2!
Ah ! Ce serait donc la régularité !
Oui sinon il doit y avoir une erreur dans ma définition de la sommation « à la zeta » pour une série de terme général a_n (au-delà du cas a_n=n qui donne Riemann)
Peut-être qu’il faut écrire
$latex \sum \frac{a_n}{n^{s+1}}$ et prendre $latex s\to -1$, plutôt ?
Oui,c’est la methode que vous donniez dans le premier billet! Je crois que lorsqu’on regularise zeta,on fait souvent plus appel a son prolongement analytique, pour lequel l’ecriture en serie n’est que formelle. C’est peut etre pour ça qu’on perd des « bonnes » propriétés..
Oui bien vu ! C’est corrigé !
Excellent billet, j’avais lu le précédent sur ce sujet.
J’apprécie d’avantage celui-ci, on sent que ce sujet à mûri dans ta tête. C’est mieux expliqué.
Ou alors peut-être que je suis devenu trop formé à lire de math post-bac du style prépas.
En tous cas, félicitation.
Dommage qu’il n’existe pas d’opérateur de sommation régulier, stable et linéaire. Ça aurait été trop beau. Cela casse tout. Peut-être peut-t-on mettre une contrainte pas trop trivialle sur les suites tel que sur ce sous-ensemble il puisse exister une tel opération.
Bonne journée/soirée.
Oui ce serait intéressant de pouvoir caractériser cet ensemble de suites pour lesquelles on sait qu’on peut trouver une méthode régulière, stable et linéaire. Car du coup, pour toutes les suites de cet ensemble les manipulations « heuristiques » donneraient des résultats corrects (en respectant les règles bien sûr !)
C’est pas si facile que cela, je pensait que les suite bornée auraient pu faire l’affaire, cela aurait été peu mais déjà bien.
Or la suite 1,1,1,1,1,1,… et bornée. Si on notait A=1+1+1+…
Par linéarité A=1,0,0,0,… + 0,1,1,1,…
Par régularité le premier terme vaut 1
Par stabilité le second vaut 0+1
Ainsi A=A+1
Donc 0=1.
C’est pas bon.
Il reste sûrement les suites de moyenne partiel convergente ( par exemple 0,1,0,1,0,1,0,1,… donc la moyenne tend vers 1/2) et l’opérateur de série serait celui de césaro. Mais cela ne marche pas non plus.
1,1,1,1,1,1,1… est encore dedans.
Il ne reste plus grand chose comme sous ensemble des suites. ( Si cela ce trouve, on peut montrer que le plus grand est celui des suites dont la suite des sommes partiels est convergente 🙂 )
C’est dommage, c’est trop restreint pour devenir intéressant. Ce qui n’enlève pas le fait que l’article est très intéressant.
si on continu a faire des calcul comme au debut:
si C=1+1+1+1…
si A=1-1+1-1… (la 1ere « calculé »)
C+A=2+2+2+2… = 2*(1+1+1+…) = 2xC
alors A=C => C=1/2 …
Bon apres on peu faire!
S-C = 0+1+2+3+4….=0+S => -C=0 ….
ceci dit en realité on a pas
2+2+2+2… mais 2+0+2+0+2… la « suppression » des 0 n’est aucune des 3 propriétés énoncé…. (et est faite dans le cas du « calcul » de S aussi!!!)
heu du coups???? S peu avoir plusieurs valeur???
la problématique dans cette facon de chercher d’est methode permetant de faire de « nouvelle » somme (moyenne de cesaro… etc) qui permettent de définir certaine de ces « limites » sont elle uniques et font elles converger ces series vers les meme valeurs?
Très bien observé pour 1+1+1+1+…
Effectivement ça montre (comme pour 1+2+3+4+) qu’il ne peut pas exister de méthode vérifiant les 3 conditions qui marche pour cette série.
D’ailleurs ça ne fonctionne pas avec Abel, puisque qu’on obtient 1/(1-x) qui a un pôle en 1…
Oups, j’ai fait une faute de frappe dans l’exemple que je donne.
A=somme(1+1+1+1+…)
A=somme(1+0+0+0+…) + somme(0+1+1+1+…) (linéarité)
A=1 + ( 0 + somme (1+1+1+1+1+…) (régularité pour le premier terme, stabilité pour le second)
A=1+A
0=1
Super article, comme toujours ! Merci pour le lien 😛
Dans mon article, je montre que toute suite définie récursivement par une formule
u(n+k) = a(0) u(n) + a(1) u(n+1) + … + a(k-1) u(n+k-1)
peut être sommée. Ceci inclut les séries géométriques u(n+1) = q u(n), et donc la somme 1-1+1-1+…
Plus exactement, il existe une unique sommation régulière, stable et linéaire définie sur la somme de l’espace vectoriel des suites convergentes et l’espace vectoriel des suites définies récursivement.
Et puisque les suites définies récursivement sont définies par un nombre fini de réels (les k coefficients a(i) et les k premiers termes de la suite), on peut en fait facilement construire un algorithme qui calcule leur somme !
Lê, cela n’est-il pas en contradiction avec le fait que 1+1+1+1+… n’est pas sommable ?
Bonjour,
Tout d’abord j’ai adoré les deux articles et tous les commentaires, quels qu’ils soient car ce sujet reste un débat, bien que je ne les ai pas encore tous lus.
Je voudrais rebondir sur la suite 1,1,1,1,1,1,… et A sa série de emynona.
Si je devrais l’écrire de la façon dont je vois les choses je mis prendrais de cette façon :
soit n un entier non nul
infini 1 infini 1 infini
A = somme (1) soit A = [somme(1) + somme(0)] + [somme(0) + somme(1)]
n=1 n=1 n=2 n=1 n=2
infini infini
on aurait donc bien A = [1 + 0] + [0 + somme(1)] = 1 + somme(1)
n=2 n=2
infini infini
Or somme (1) est différent de somme(1) est donc cette somme serait différente de A car elles ne commenceraient pas au
n=1 n=2
même rang bien que les deux soient infini elles n’en sont pas égales
Pour revenir au même rang il faudrait passer par un changement de variable du style p = n-1 dans ce cas on a:
infini infini
Somme(1) = somme(1) = P soit au final A = 1 + P et non A = 1 + A qu’en pensez vous ?
n=2 p=1
1 « J’émets une réserve quant à vos calculs qui au demeurant sont justes. Je pense que les valeurs de S comme de B prises séparément restent incalculables car infinies ; et que cette égalité S = – 1/12 n’est pas le résultat de la valeur de S, mais plutôt le résultat du rapport de grandeur existant entre S et B.
En analysant cette suite numérique (1+2+3+4+5+6+7+…) deux choses sautent aux yeux. La première est le résultat qui est nécessairement positif ; et la seconde est l’infini qui par définition signifie : « Qu’on ne peut évaluer, qui est incalculable. »
Or cette égalité S = – 1/12 aboutit au résultat suivant : – 0.083 qui plus est un résultat négatif. »
2 « Ce qui est dommage dans ce post, ce n’est pas tant ce que vous en dites, mais plus ce qu’on en retient. On en retient que les mathématiques sont conditionnées ; et en cela, elles sont restrictives. On ne peut lutter contre une ineptie que par un contre-exemple.
Pouvez-vous trouver la valeur de cette suite numérique ? : (7+81+23+14+12000+45+…). Je confirme qu’il s’agit bien d’une somme infinie et que les chiffres se succèdent de façon aléatoire. Vous ne pouvez pas, n’est-ce pas ? Votre échec patent prouve que ne peut pas tout mathématiser ; et du même coup, redonne ses lettres de noblesse à ma définition première : « l’infini qui par définition signifie : Qu’on ne peut évaluer, qui est incalculable. »
—————————————————————————–
3 Ci-dessus, je retranscris mes anciens commentaires, afin de les compléter d’un troisième. Je vous propose l’égalité suivante : 1+2+3+4+5+6+7+… = 7+81+23+14+12000+45+… Toutefois, je précise que la deuxième valeur est bien une somme infinie et que les chiffres se succèdent de façon aléatoire sans jamais se répéter. Mon égalité me semble juste tout en respectant la commutativité inhérente à l’addition. Pourquoi ? Parce que sans même réaliser un seul calcul, je peux prendre n’importe quelle valeur et dire qu’elle est égale à elle-même, ce que mon addition démontre puisque sa simplification est ∞=∞. Et puis tiens ! soudainement, il me vient l’idée qu’il serait peut-être possible d’avoir -1-2-3-4-5-6-7… = +1/12 juste comme ça en passant.
Bien à vous…
C’est dommage que vous voyez ceci de cette façon. Vous êtes choqué car cela ne vous parait pas « naturel ». Mais si on y réfléchit bien, rien n’est naturel. C’est comme si on donnait les nombres relatifs à quelqu’un qui ne connaît que les nombre positif. C’est a dire ajouter des « nouveaux » nombres tels que pour tout les « anciens », il en existe un avec qui la somme fait 0 et qu’on puisse étendre l’opération d’addition avec ceux-ci. La personne nous dira que si on somme 2 nombres, on ne peut que augmenter (la somme de deux positif fait augmenter le nombre) et qu’on ne peut espérer atteindre 0. ( où d’autre qu’on ne peut définir de série à terme positif dont la valeur serait négative ). Bref que ceci n’a aucun sens. ( On peut transposer cet exemple aux rationnel, réels, complexes.
Il faut juste comprendre que tout en math est issus d’une certaine construction et que tout choses doit être entièrement défini de sorte que toute phrase puisse être indiscutée. Par exemple vous parler de quelque chose d’aléatoire, l’aléatoire dont dans le sens commun n’existe pas en math ( même pas en probabilité 🙂 , on fait que des manipulation de nombre et tout est strictement défini )
C’est cela qui est vraiment sympa en mathématique. Tout doit être à la fois strictement énoncé mais on a une liberté infini d’inventé nos définition.
Bonne soirée.
« Mais si on y réfléchit bien, rien n’est naturel. »
Cette phrase m’indique qu’il n’est pas besoin de réflexion ou si peu pour être mathématiciens. Gaston Bachelard les nommait ces prophètes de l’abstrait. A l’inverse, n’importe quel penseur pourrait vous démontrer que tout est naturel. Le soleil est un générateur de lumières comme l’homme est un générateur de pensées ; de l’un naissent les fleurs ; de l’autre, les idées. En cela, il n’est rien dans l’Univers qui ne soit contre-nature, sauf à considérer l’espèce humaine sans appartenance. L’Univers est régit par la loi des possibles, rien d’autres.
Bien à vous…
Correction : c’est écrit par Bourbaki (qui s’en excusait, je crois) : la série des entiers « naturels » (justement) « 1,2,3,4,… » ne pourrait pas se définir, et serait donc, justement « naturelle ».
Sur cette série est définie l’addition, telle qu’on la connait. Si on lui cherche un élément neutre, on n’en trouve pas, et on décide donc de l’inventer (et il n’est donc pas « naturel ») : zéro.
Après, on cherche des symétriques à chacun des membres, et on ne les trouve pas, et on invente les « entiers négatifs ».
Et ainsi de suite (Ah, math sup/math spé !!!)
Dans cette logique, je suis les définitions des méthodes « linéaires, régulières et stables », mais sans vérifier plus avant la façon dont ces critères sont appliqués dans les calculs, il me semble que le calcul « heuristique pour la série A=1/2 est correct, mais pour les deux autres, il y a changement de l’ordre des termes, non ?
J’ai cru aussi, mais en fait, non il n’y a pas changement de l’ordre des termes, il y a par contre application bête et méchante de la linéarité.
Ca passe un peu inaperçu, car un point a été un peu dissout dans les écritures. Parfois on y remplace 3 par (2 + 1), (juste un exemple), ainsi de 3 + 4 on pourrait arriver à (2+1) + (3+1) et pas 2 + 1 + 3 + 1 car l’associativité n’est plus remplie. On a pas (2+1) + (3+1) = 2 + (1 + 3 + 1) (juste un exemple). Ainsi il n’est en fait pas justifié de retirer les parenthèses et en toute rigueur, tout l’article aurait pu et du les conserver.
Enfin, il me semble.
Quand on parle de mathématique, le mot « naturel » devrait s’en ternir à une définition technique, comme les nombres naturels.
Le mot naturel n’a une définition que consensuelle. Le concept de « naturel » est un des plus controversés et pour cause, il est toujours subjectif.
Cela dit, dans la définition la plus courante de « naturel » que j’ai pu rencontrer, les maths n’ont effectivement rien de naturel. Je compléterai donc l’assertion de emynona : « En maths, rien n’est naturel dans le sens commun du terme ».
Je trouve vraiment surprenant de voir que vous continuez à ne pas vouloir penser possible ce que démontre ce billet alors que celui-ci répond justement aux remarques que vous repostez ici. Soit vous n’avez pas envie de penser autrement et n’évoluerez pas dans votre façon de voir/utiliser les maths (ce qui n’est pas en problème en soi, ça dépend de ce que vous en faites)), soit vous vous dites « mes certitudes n’en sont peut-être pas, essayons de comprendre et de vraiment s’intéresser à ce qui nous paraît absurde ».
Juste une petite précision, attention lorsqu’il s’agit de manipulations d’infinis!!
Exemple:
Si on choisi un modèle où 1+2+3+….=infini, (ce qui est possible, mais dans ce cas on se place non plus dans R mais dans la droite réelle achevée pour l’ensemble d’arrivée de l’application somme), on se retrouve aussi avec 0+1+2+3+…=infini, donc 0+1+2+3+…=1+2+3+… et alors, par différence, (1+2+3+…)-(0+1+2+3+…)=0 or par linéarité, cela donne (1+1+1+1+…)=0 ie 0=infini!!
On a comme une contradiction! Bon là je l’ai fait salement, c’est parce que j’ai repris l’argument « l’infini, c’est l’infini », mais même sans ça, 0+1+2+3+…=1+2+3+… c’est l’axiome de stabilité!
Toujours dans la même veine, toujours en utilisant nos trois axiomes, je vais montrer que pour tout a dans IR, a=0: en effet, on a a+a+a+… = 0+a+a+… par stabilité, ensuite, en faisant la différence, 0=(a+a+a+…)-(0+a+a+…) ce qui donne par linéarité de la somme 0=a+0+0+… soit par régularité, a=0, CQFD
Il résulte de ce puissant théorème que tous les nombre réels sont égaux, et ils sont égaux à l’infini!
Biensûr tout ceci est parfaitement absurde et ne montre que le fait qu’un opérateur somme qui manipule des sommes infinies ne peut pas être à la fois régulier, linéaire et stable. En fait il devient non linéaire dès que l’infini apparaît, et donc ce ne sont pas des opérateurs tout le temps satisfaisant, il prolongent assez mal les opérateurs de somme sur les séries absolument convergentes, c’est pour cela que l’on veut aller en chercher un autre, même si a priori cela semble bizarre qu’il donne une somme négative…
On a en fait pour cette série deux notions de somme qui sont différentes et on choisit l’une ou l’autre selon le contexte, rien de plus.
Quand à savoir si c’est « naturel » ou pas, rappelez vous un peu les problèmes qu’ont posé à l’ensemble des communautés scientifiques de l’époque les nombres irrationnels, transcendants, complexes, le paradoxe de Russel, les travaux de Cantor, de Gödel, et j’en passe…
Rien n’est naturel, dans un cadre logique fixé, les choses sont ce qu’elles sont (ne parlons pas des indécidables) et elles nous semblent plus ou moins intuitives, mais l’intuition change, alors que tout ce dont on parle est immuable, une fois le cadre posé. Le « problème » soulevé par ce résultat négatif est purement subjectif, la conpréhension est peut être partielle sur ce sujet, mais à n’en pas doûter un opérateur de somme satisfaisant à tous les niveaux même pour les séries divergentes existe ou n’existe pas
Merci pour l’exemple de a+a+a+a+… Effectivement cela montre bien qu’il existe un tas de séries non-sommables par une méthode régulière, stable et linéaire !
Ce qui me parait le plus contestable c’est de dire que si a est infini et b est infini, alors a=b !!!!!!!!!
Ne peut-on pas simplement restreindre la stabilité à tout nombre différent de 0 pour résoudre toutes les remises en question sur l’existence d’une méthode stable, linéaire ?
Ainsi que de poser qu’à l’intérieur d’une somme infinie, pour tout ai, bi : ai + 0 + bi = ai + bi.
Un étudiant en physique sait que l’infini n’est jamais très loin. En optique géométrique, il suffit généralement de se placer à plus de 5m d’une focale pour considérer la distance infinie. En chimie, 1mm est plus que suffisant pour que les interactions entre molécules soit négligeables car à l’infini l’une de l’autre. L’infini est une notion abstraite, relative, présente dans tous les domaines, et c’est notre conception limité de l’univers qui limite son appréhension.
Par densité, il existe une infinité de nombre rationnels sur intervalle [0;1] de l’espace des réel.
Il est facile de considérer cette affirmation ‘naturelle’. Pour deux points de ce segment, on pourra toujours en trouver un troisième situé entre les deux premiers.
Voilà un exemple d’infinité dont même un élève de CP peut faire l’expérience sans en maitriser les concepts mathématique sous-jacent.
Les deux articles précédents sont une vulgarisation scientifique (très pédagogue) d’un paradoxe mathématique fascinant, dont les physiciens n’ont pas attendu la démonstration formelle pour le mettre en pratique (l’histoire se répète bien souvent).
Considérer le problème avec hauteur en déclarant « cette phrase m’indique qu’il n’est pas besoin de réflexion ou si peu pour être mathématiciens » constitue pour moi un manque flagrant de compréhension et un manque de respect pour une science des plus rigoureuse.
Peut être l’emploi du terme « naturel » vous a-t-il choqué ? Corrigez-le par « intuitif ». Les mathématiques nous apprennent à développer notre intuition tout autant que de nous en méfier.
Excusez mon ton vindicatif et mes éventuelles fautes d’orthographes (j’ai mes lacunes). J’espère que ce long texte vous aura donné matière à réflexion.
Ma phrase n’est que le déni d’une autre ; en cela, seulement, elle est irrévérencieuse. Maintenant, elle ne possède pas l’aspect universel que vous semblez lui prêter. J’ai pour usage de toujours séparer les matières d’étude et ceux qui les pratiquent ; car si la matière prédominait, il n’y aurait jamais de découvertes ni d’avancées.
« Par densité, il existe une infinité de nombre rationnels sur intervalle [0 ; 1] de l’espace des réel. Pour deux points de ce segment, on pourra toujours en trouver un troisième situé entre les deux premiers. »
Je suis en contradiction avec ce toujours ; car pour moi, il n’existe pas d’infini vers l’infiniment petit. Il existe un point au-delà duquel la matière ne peut aller, une criticité subatomique bien supérieure à celle de l’atome qui est à l’origine de la formation des trous noirs ; en considérant que chaque trou noir, en atteignant sa taille définitive, reproduit en son centre les caractéristiques physiques d’un Big Bang.
Ce toujours est valable, à la condition qu’il n’existe pas de singularité gravitationnelle.
Bien à vous…
Décidément, vous n’avez pas l’air de maîtriser beaucoup les mathématiques et vous interprétez tout à votre sauce ! Votre problème, c’est que vous essayer de trouver un cadre « réel » aux mathématique, sans en comprendre la notion ! Toutes les mathématiques sont fondé sur des axiomes : il s’agit déjà d’un cadre !
Pour répondre à votre dernier commentaire , vous considérez qu’il n’y a pas d’infini vers le petit…c’est « votre » définition, et elle n’est pas rigoureuse même si elle pourrait avoir un sens physique ! En mathématique, quelque soit l’exemple que vous pourrez me donner, il y aura toujours « plus petit ».
Concernant votre premier commentaire, vous manipulez le « hasard », qui n’est, à mon sens, pas un objet mathématique (« de façon aléatoire » n’a ici aucun sens. Si ça en avait, ça ferait longtemps qu’on aurait une sécurité maximum sur les cryptages).
Deuxièmement, vous manipulez l’infini avec des moufles ! Deux infinis ne sont pas forcément « égales » et ce sont des maths élémentaires : certains convergent plus vite que d’autre, et l’égalité n’a alors aucun sens !
Bien sur, étant donné que :
-vous faite de la mathématique de « compréhension » au doigt mouillé (« je penses que » n’est pas une démonstration et un « rapport de grandeur » est généralement une division, pas une soustraction )
-vous dénigrez aisément la recherche fondamentale (Votre commentaire sur les « matière d’étude et ceux qui les pratiquent » n’a aucun sens en math …Contrairement à la physique, les mathématiques restent abstraites, et n’ont pas de « domaine d’application » à proprement parlé…ce sont plutôt les autres domaines qui utilisent des outils mathématiques)
-vous faites de la philosophie de comptoir (les mathématiciens « de peu de réflexion » vous disent merci)
…vous ne cherchez pas à comprendre les enjeu derrière et comment ces prolongements peuvent être utiles.
Vous arborez peut être un ton respectueux, mais à venir prendre les autres de haut avec vos grands sabots, le contenu ne l’est pas : vous m’êtes très désagréable (ce qui explique mon propre ton de réponse) !
Bien à vous également !
Laurent T
Bonjour !
Je suis élève en terminale S. Je n’ai donc pas compris grand-chose de ce billet-ci (et je ne l’ai en fait pas lu jusqu’à la fin) mais le précédent sur le sujet m’a vraiment intéressée (cependant je ne comprend pas bien l’étape où on passe de B = 1 – (2 – 3 + 4 – 5 + 6 – 7 +…) à B = 1 – (1 – 2 + 3 – 4 + 5 – 6 + 7 – …) – (1 – 1 + 1 – 1 + 1 – …) ?)
Sur le coup ça m’a semblé absurde, et jusque là j’aurai immédiatement répondu que la somme est égale à l’infini mais les calculs semblent se tenir, même si je continue de trouver cela étrange ahah
Laurent, par rapport à ce que vous dites sur le fait que deux infinis ne sont pas toujours égaux, est-ce que cela peut se « quantifier » ou non puisque par définition l’infini est « inquantifiable » ?
Je m’explique, il y a une infinité de nombres entre 1,1 et 1,2. Mais il y a également une infinité de nombres entre 1 et 2. Et puisque entre 1 et 2 il y a 10 fois l’écart qu’il y a entre 1,1 et 1,2 (dans le sens que 0,1*10=1), est ce qu’il est absurde de considérer que « infini entre 1 et 2 = 10*(infini entre 1,1 et 1,2) » ?
Mais en tout cas c’était très intéressant, ce sont ce genre de sujets qui me donnent envie de continuer les maths dans le supérieur! Merci 🙂
Pour Léaa : non, les infinis entre 1 et 2 et entre 0.1 et 0.2 sont « de même ordre ». De mémoire (mes math sup et spé sont quand même loin !) on peut définir 3ordres d’infinis, dénommés ALEPH 1, 2 et 3 ALEPH est un caractère de l’alphabet hébreu). L’ALEPH 1 est celui des infinis isomorphe aux entiers naturels (on peut numéroter de 1 à autant qu’on veut les éléments de l’ensemble considéré). L’ALEPH 2 est celui des ensembles isomorphes aux réels (il y a toujours un élément de l’ensemble « entre » deux éléments quelconques – « entre » suppose une relation d’ordre dans l’ensemble), et l’ALEPH 3, c’est tous les autres.
Merci de me rafraichir la mémoire si j’ai dit des bêtises.
Petite imprécision de ma réponse : le cardinal des entiers naturels est l’ALPH 0. Pour les réels, c’est ALEPH 1. J’ai dit ensuite que l’ALEPH suivant était le cardinal des ensembles ordonnée infinis qui n’étaient ni ALEPH 0, ni ALEPH 1 : ce n’est théoriquement pas juste : en théorie, il existe une infinité d’ALEPH successifs. Mais ça n’est pas complètement faux non plus, car on ne connait pas (si j’ai bien compris Google) d’ensemble de cardinal supérieur à l’ALEPH 2.
Excellent! Je plussoie totalement. Un grand merci d’avoir osé l’écrire.
Et merci David pour cet article de qualité! C’est vraiment dommage que peu sachent apprécier ce thème intéressant à sa juste valeur.
Bien cordialement,
Manu
TG
Les nombres négatifs viennent d’une logique imposée au réel.
Cela me rappelle l’émission sur Pi où le présentateur disait : « Si j’ai moins un poisson, et qu’on me donne un poisson, j’ai la certitude de ne pas avoir de poisson du tout » ;
J’avais mis en commentaire que la phrase était absurde et ne prenait de sens qu’en y ajoutant la notion de dette : si je dois un poisson et qu’on m’en donne un, après règlement de ma dette, je n’ai plus de poisson !
L’écriture mathématique 0-1=-1 est abusive, et vient du désir de formuler une logique ! Et l’on voit ainsi poindre toute sorte de confusions, car d’un point de vue purement arithmétique 0-1 ou -(ce qu’on voudra) sera toujours égal à 0, car on ne peut rien soustraire à l’absence de quantité.
Je rappelle aussi que le terme « infini » pour désigner ce qu’on ne peut calculer est impropre et doit être remplacé par le terme « indéfini », et ainsi l’on comprendra aisément que 1+2+3+4+5… peut-être plus petit, plus grand ou égal à 7+81+23+14+12000+45… le terme devant être strictement réserver à ce qui n’a réellement pas de limite et non point dévolu à ce qui n’est qu’indéfinissable !
Néanmoins, si l’on me donne 1€+2€+3€… je vais finir par épuisé cette matière dans l’univers, et je me retrouverai dans la logique paradoxale de soustraire à ma somme, si je veux continuer à en « rajouter ». Je peux m’amuser à soustraire indéfiniment pour en « rajouter », ce qui n’augmentera pas la limite atteinte d’un iota ! Mais je peux m’amuser à formuler « limite »-1+1+ »limite »-1+1… indéfiniment !
En mathématiques, 0-x = -x n’est pas le fruit d’une logique imposée au réel. C’est le fruit de l’application d’une définition : celle de la soustraction. Mais en mathématiques, rien ne vous empêche de définir que la soustraction a – b vaut max(0,c), ‘c’ étant l’unique entier positif tel que c+b = a. Autrement dit que a-b vaut soit a-b, si c’est positif, soit 0. Dans cette arithmétique, on va par contre avoir des résultats du type : 3-5+2 = 4. Il y a peut-être des domaines du réel où ça a un sens, peut-être pas. Ce n’est pas au mathématicien d’en juger.
Correction : 3-5+2 = 2 dans cette arithmétique. Pardon.
Je pense que vous faites une confusion sur la nature des mathématiques.
Pour définir une opération comme 3-5(ou n’importe quelle opération), on n’a absolument pas besoin de faire quelque référence que ce soit au monde matériel et concret. Ce qui importe, c’est la cohérence logique. C’est particulièrement évident avec la construction des nombres: les irrationnels , les nombres négatifs, les nombres imaginaires ont tous en leur temps choqué parce qu’on ne leur trouvait pas de sens « concret ».
On considère que 3-5 = -2 parce que c’est cohérent avec les définitions que l’on fait des entiers relatifs et de la soustraction.
Pingback: Le scandale des séries divergentes ! (ou...
Très bon billet encore une fois, merci beaucoup! Je trouve comme tout le monde dommage qu’il n’y ait finalement pas d’opérateur de sommation « propre » pour prouver S=-1/12, mais c’est la vie…
à propos de la commutativité, cela me rappelle un joli problème: quelles sont les permutations pi:N->N qui préservent la convergence de toute série ? (pas facile!)
PS: un seul « m » à Ramanujan 😉
Pour le problème, je passe 🙂
Mais pour Ramanujan, je corrige de ce pas !
Décidément c’est la période, Numberphile aussi avait sorti sa vidéo sur le sujet :
http://www.youtube.com/watch?v=w-I6XTVZXww
Oui je crois que c’est cette vidéo qui rallumé le feu en fait. Elle a inspiré l’article de Bad Astronomy que je cite, ainsi que la vidéo de « e-penser » sur le même sujet.
J’avais noté depuis quelques jours un regain de connexions sur mon ancien billet sur le sujet, tout s’explique maintenant !
Beau travail ! J’ai lu les deux billets avec un égal plaisir, alors même que la surprise était passée pour le plus récent, preuve de la qualité du 2ème.
Un de mes anciens profs de maths a partagé ça sur google+ (accessible en mode public). Je n’ai pas tout compris mais j’ai l’impression qu’il va encore plus loin que vous !
https://plus.google.com/u/0/114134834346472219368/posts/ZuJDv3daT9n
Merci.
C’est intéressant de se faire démontrer des choses fausses !
Mais pour le non mathématicien que je suis, je trouve qu’il y a du mou dans la corde à noeuds (expression reprise de mon illustre prof de math de fac) sur ce point:
vous insistez sur le fait que
« quand on a une somme d’un nombre infini de termes, la valeur de la somme peut dépendre de l’ordre des termes ! », il n’y a pas de commutativité, etc…
Mais cela ne vous empêche pas d’utiliser intensément
A = ET B = => A+B =
Ca me semble contradictoire. Et visiblement, il n’y a pas implication.
Donc dés la premières ligne, si ca se trouve, c’est faux:
A = 1- 1 +1 -1 ….
n’implique peut être pas que A = 1- ( 1 -1 +1 -1 … )
Jusqu’à preuve du contraire 😉
Vous confondez commutativité et linéarité :
La commutativité c’est le droit de faire une permutation des termes de la suite, la linéarité c’est le droit d’additionner deux suites termes à terme.
Le fait de mettre des parenthèses sur une partie de la suite, pour pouvoir la factoriser par -1, je considère que c’est utiliser la commutativité: on change l’ordre d’application de la somme.
Le fait de pouvoir associer comme on veut les nombres en groupes parenthésés pour calculer une expression, s’appelle l’associativité, et elle n’a pas de lien direct avec le fait de pouvoir faire les opérations en changeant l’ordre des termes (voir l’exemple 16 de http://devys.cpge.voila.net/Complements/groupes_anneaux.pdf). De plus ici ce n’est par réellement l’associativité que l’on utilise, mais l’axiome de stabilité, qui, si on considère la somme infinie comme prolongement de la somme usuelle (donc qui garde les mêmes propriétés) découle de l’associativité de cette derniere.
Ce qui peut troubler est qu’effectivement on effectue les opérations dans un autre ordre, mais c’est pas comme si on permutait, en réalité, chaque nombre reste à sa place.
De plus, on perd la commutativité, mais pas tout à fait quand même, même pour une série convergente non absolument convergente, on ne changera rien à la somme en ne permuttant qu’un nombre fini de termes, pour changer cette somme, il faut obligatoirement bouger un nombre infini de termes
La démonstration est simple: on prend une série Somme(a_n), si on change la place de N termes, alors on dispose de K tel que tous les nombres qu’on a bougé partent d’un indice plus petit que K et arrivent à un indice plus petit que K. Notons Somme(b_n) la série d’arrivée:
On a a_n=b_n pour n >K.
donc Somme(a_n) = a_1+…+a_K + Somme(a_n, n>K) = a_1+…+a_K + Somme(b_n, n>K),
or a_1+…+a_K = b_1+…+b_K (ce sont les mêmes termes, mais permutés dans une somme finie, où l’on a commutativité)
donc Somme(a_n)=b_1+…+b_K+Somme(b_n, n>K)=Somme(b_n) CQFD
Je pense que ce petit exercice vous permettra de mieux comprendre et distinguer les différentes notions abordées
Correction de mon post ci dessus, qui a mal pris que j’utilise les caractères ‘inférieur’ et ‘supérieur’ ( et je ne vois pas comment le changer )
Merci.
C’est intéressant de se faire démontrer des choses fausses !
Mais pour le non mathématicien que je suis, je trouve qu’il y a du mou dans la corde à noeuds (expression reprise de mon illustre prof de math de fac) sur ce point:
vous insistez sur le fait que
« quand on a une somme d’un nombre infini de termes, la valeur de la somme peut dépendre de l’ordre des termes ! », il n’y a pas de commutativité, etc…
Mais cela ne vous empêche pas d’utiliser intensément
A = « écriture 1 » ET B = « écriture 2 » => A+B = « mix des écritures 1 et 2 »
Ca me semble contradictoire. Et visiblement, il n’y a pas implication.
Donc dés la premières ligne, si ca se trouve, c’est faux:
A = 1- 1 +1 -1 ….
n’implique peut être pas que A = 1- ( 1 -1 +1 -1 … )
Jusqu’à preuve du contraire 😉
La vidéo de Numberphile a également donné lieu à cet article : http://blogs.scientificamerican.com/roots-of-unity/2014/01/20/is-the-sum-of-positive-integers-negative/ ; ce dernier donne en conclusion beaucoup de liens sur le même sujet.
Pour ma part, en tant qu’(ex-)physicien, le fait que la Réalité elle-même prouve que la somme considérée vaille bien -1/12 par l’intermédiaire de l’effet Casimir me suffit amplement.
À moins que… (lire, de Greg Egan, les nouvelles « Radieux » dans le recueil homonyme et sa suite « Les Entiers sombres » dans le recueil « Océanique » ;). Je ne suis pas fan des romans de Greg Egan, mais ses nouvelles sont des merveilles !)
La somme considérée ne vaut pas -1/12. Alors, qui se trompe ? La réalité ? Ou les physiciens qui appliquent la formule de Casimir sans trop chercher à comprendre ? 😉
Le fait que le résultat -1/12 trouve une application en physique montre en tout cas que ces calculs, aussi déroutants qu’ils puissent paraître disent quelque chose sur le réel tel que nous le mesurons. Ce n’est pas une preuve au sens mathématique mais c’est un indice fort sur le fait que cette démonstration contient une forme de vérité qu’il appartient aux mathématiciens d’expliquer, sans pouvoir l’écarter d’un haussement d’épaule. Imaginons un berger qui aurait un troupeau de mouton infiniment grand, sur le dos de chacun des moutons on inscrit un nombre incrémenté de 1 à chaque foi, si l’on fait la somme de ces nombres et que l’on arrive à -1/12 alors les mathématiciens seraient appelés à expliquer ce phénomène. C’est exactement ce qu’a fait Casimir, en mécanique quantique certes, mais les troupeaux de moutons infinis sont assez rare dans la nature alors que les ondes….
A moins que vous ne vous adressiez à des physiciens à l’honnêteté intellectuelle douteuse, vous découvrirez que le résultat physique utilisé est obtenue par la formule d’Euler-Maclaurin, qui donne : \left(\sum_n n – \int x\ dx\right) = – 1/12
Autrement dit, on a 1+2+3+… = l’infini -1/12… Ce qui n’est pas tout à fait la même chose. Cependant, dans le cadre d’un calcul de dérivée, on arrive à annuler le terme infini, ce qui fait que, si on n’a pour la rigueur mathématique qu’un goût peu prononcé, et qu’on préfère utiliser des formules toutes faites sans trop chercher d’où ça sort, en effet, on peut utiliser 1+2+3+… = -1/12 et obtenir le bon résultat. De la même façon que la dérivée de 1+x = 1 et la dérivée de 2+x = 1 peut donner l’impression que 1+x = 2+x.
@vincent
« Le fait que le résultat -1/12 trouve une application en physique montre en tout cas que ces calculs, aussi déroutants qu’ils puissent paraître disent quelque chose sur le réel tel que nous le mesurons »
Ca peut aussi signifier que le phenomène est faux. (n’existe pas tel que defini. Et de là on en apprendrait baucoup plus sur la remarquable efficacité des mathématiques).
Je ne comprends pas la moitié de ce qui est ecrit dans cet article, mais franchement je suis fasciné par ce tryptique de propriétés de sommation.
Peut etre qu’on prend ce problème par le mauvais bout. Est ce qu’on peut reduire le problème de definition des propriétés de sommation à un problème de geometrie ou topologie.
F.L.
C’est idiot, on peut réordonner des séries de ce genre pour « converger » vers tous les réels qu’on veut.
Un exercice très simple, qui généralise votre blabla sans vous contredire :
soit
u_n –> +infty
v_n –> +infty
u_{n+1}-u_n –> 0
montrer que (u_n-v_m)_{n,m>0} est dense dans IR.
et là c’est des vraies maths, il n’y a aucun paradoxe.
Dois-je comprendre que vous faites des vraies maths, et moi du blabla et des fausses maths, c’est bien ca ?
En plus ce résultat est déjà mentionné dans le billet, section « bye bye la commutativité »
Bonjour! Je suis tombe par hasard sur votre blog il y a quelques jours… Bravo et merci, je crois que je n’avais jamais rencontré une telle variété avec de telles qualités pédagogiques sur internet! Cet article était très intéressant, je trouve dommage que certains aient cette manie de taper sur tout ce qui dérange un peu leur confort et leurs habitudes. Ne vous découragez pas surtout! 🙂
Juste par rapport au commentaire de ab : son exercice ne généralise rien du tout car la troisième hypothèse n’est pas vérifiée : comme les séries qui apparaissent dans cet article ont des termes entiers, je ne vois pas comment on pourrait les écrire comme une différence de 2 suites qui tend vers 0! Du coup, ça a bien un intérêt de se demander si la somme peut être étendue a des series divergentes (peut-être existe-t-il des series divergentes dont la somme serait bien définie? En tout cas, le probleme mérite d’être pose et ne semble pas se réduire au corollaire d’un exercice de prepa)
PS : désolé de déterrer un commentaire vieux de 2 ans pour si peu, en fait au départ je voulais surtout vous féliciter, mais je n’ai pas pu m’empêcher d’examiner la remarque de ab (tout votre article aurait été perdu, ç’ aurait ete dommage quand même!). En tout cas, j’espère vraiment ne pas déclencher un nouveau conflit mondial sur votre blog! Si c’est le cas…. Désolé :p
Je suis entièrement d ‘accord avec le commentaire de Pierre.
Pierre Lescanne
A=1-1+1-1+1-1+…
A=1-(1-1+1-1+1-1+…)
A=1-A
Puisqu’on a A = 1-A, on peut déduire que A=1/2.
A=1-1+1-1+1-1+…
A=1-(1-1+1-1+1-1+…)
A=1-(1-(1-1+1-1+1-1+…)
A=2-A
Puisqu’on a A = 2-A, on peut déduire que A=1.
Donc 1/2=1=∞
?
Ah, là c’est facile ! Simple erreur de calcul.
Là où tu as écris « = 2-A », tu aurais du écrire « 1-(1-A) » qui vaut « A » et non pas « 2-A » 😉
Autant pour moi (ou « au temps » il parait…)
Je n’ai pas lu tout le billet, et je le ferai, presque promis,
Quelque chose me chiffonne:
A=1-1+1-1+1-1+…
A=1-(1-1+1-1+1-1+…)
A=1-A
Puisqu’on a A = 1-A, on peut déduire que A=1/2.
Jusque là tout va bien
A=1-1+1-1+1-1+…
A=(1-1)+(1-1)+(1-1)+…
A=0+0+0+…
A=0
Où est l’erreur?
A=1+(-1+1)+(-1+1)+(-1+1)+…
A=1
Où est l’erreur?
ça y est.. je n’ai pas tout compris, sinon qu’avec des méthodes différentes on tombe sur les mêmes résultats
encore merci pour votre site
Le fait de placer des parenthèses parait relativement innocent, mais c’est une possibilité qu’on perd dès que l’on utilise certaines méthodes de sommation étendues. Ca n’a l’air de rien, mais c’est une transformation non-linéaire dans l’espace vectoriel des suites !
Placer des parenthèses où on veut revient à prendre des suites extraites de la suite (S_n) des sommes partielles (ici, ce sont la suite des termes d’indice pair (S_{2n}) et ceux d’indice impair (S_{2n+1}))
La série étant divergente (au sens classique du terme), la suite de ses sommes partielles diverge, et il n’y a aucune raison que ces sous-suites convergent vers la même chose.
C’est pourquoi cette opération est « interdite »
Votre deuxième calcul aboutit à A=A.
Si on avait aboutit à une contradiction, la conclusion aurait été « il n’existe de pas de sommation stable, …, … qui soit défini sur un sous-espace vectoriel stable … qui contient la suite testée ».
Tiens au fait le sous-espace doit être stable par décalage (shift). Je ne l’ai pas vu passer dans le texte.
Ah oui, exact pour la condition sur le sous-espace. C’est obligatoire si on veut la stabilité de l’opérateur de sommation !
Encore merci pour ce blog toujours très bien documenté et très agréable à lire.
Il me semble que pour les sommes qui convergent suivant la méthode de Césaro, on peut démontrer la régularité, la linéarité et la stabilité. Donc pour les sommes qui répondent à ce critère on peut appliquer ces règles pour de calcul. Cela justifie les calculs de A et B en début de billet.
La somme 1+1+1+1…. ne converge pas avec la méthode de Césaro : on ne peut donc pas appliquer les règles proposées. Réciproquement le fait que l’on puisse trouver deux calculs respectant les règles de régularité, linéarité et stabilité qui donnent des valeurs différentes montre que cette somme ne converge pas avec la méthode de Césaro.
La somme 1+2+3+4+5… ne converge pas suivant la méthode de Césaro. Mais il me semble aussi que dans le calcul proposé en début de billet on n’utilise pas la stabilité, mais une autre règle qui est la suivante (en plus de la linéarité) :
0+2+0+4+0+6+0+… =2+4+6+…
Autrement dit on accepte d’extraire la suite des zéros aux rangs impairs. Il me semble donc que pour étendre la somme suivant le critère de Césaro afin d’inclure 1+2+3+4+… tout en gardant la régularité et la linéarité, on a besoin de remplacer la règle de stabilité par une autre, qui permet d’extraire les zéros de rang impairs.
Je ne sais pas si l’extraction de la suite des zéros aux rangs impairs est une règle qui peut être déduite de la régularisation par la fonction zêta. Je vais y réfléchir….
En tombant sur votre question, je me permets d’y répondre malgré ça vieillesse :
Vous avez raison, Césaro ne permet pas de sommer les séries de cette façon. Il faut faire appel à Abel, puis à Dirichlet. La ligne qui vous perturbe, notamment, doit être effectuée avec la représentation en série de Dirichlet :
Considérons la série S-B = 0 + 4 + 0 + 8 + 0 + 12 + …
La série de Dirichlet associée est : 0/1^s + 4/2^s + 0/3^s + 8/4^s + 0/5^s + 12/6^s + … = 4/2^s + 8/4^s + 12/6^s + …
En mettant 4/2^s en facteur, on obtient : 4/2^s * (1/1^s + 2/2^s + 3/3^s + …)
On retrouve en facteur de droite la série de Dirichlet associée à 1 + 2 + 3 + 4 + 5 + …
De là, on peut finalement écrire que S-B=4S
Perso, je n’ai pas compris pourquoi la mise en facteur a permis de faire disparaitre les 0.
désolé peut-être, je dois avoir peut-etre rien compris vu que je ne comprends même pas la mise en facteur.
La question est pertinente. En fait, le vrai problème au coeur de toute cette polémique, c’est les notations. On écrit 1+2+3+… = -1/12 alors que le + ici n’a rien à voir avec le + qu’on connaît. Il faudrait normalement écrire f(1,2,3,…) = -1/12 où f serait une forme linéaire. On note tout de même 1+2+3+… simplement parce que pour des suites finies, f(a1,a2,…,an) = a1+a2+…+an. Ce n’est par contre plus vrai pour les séries infinies, mais on conserve la notation.
Pour répondre à votre question, quand on utilise la représentation de Dirichlet, le + utilisé, cette fois, est bien le + que l’on connaît. Cela signifie que l’on peut supprimer les 0, utiliser la commutativité, etc. Par contre, il faut garder en tête que cette représentation n’est valable que pour certaines valeurs de s, de façon à ce que la somme converge. On s’intéressera plus tard à la limite quand s tend vers 0 de cette série. Vous voyez que 1/1^s + 2/2^s + 3/3^s + … tend vers 1+2+3 quand s tend vers 0.
Ce qu’il faut retenir :
1+2+3+… pas égal à -1/12, mais f(1,2,3,…) = -1/12
a1+0+a2+0+a3+0+… = a1 + a2 + a3 +… (en tout cas, tant que la somme converge)
f(1,0,2,0,3,0…) pas égal à f(1,2,3,…) (pas de méthode de sommation stable et linéaire)
En espérant avoir répondu à votre question.
Pour la mise en facteur, faites le développement.
Gardez en tête que 2^s*2^s = 2^2s = 4^s
A=1-1+1-1+…-1=1-(1-1+1-1…)=1-A’
si dans le premier A il y avait infini de nombres
dans le deuxieme A’ il y a infini moin un
Ma question est que plus l’infini moin un vaut il plus l’infini ?
Merci pour votre billet bien expliqué.
Je pense que le mieux pour se convaincre de la réponse à cette question est de regarder les nombres entiers naturels (0;1;2;…) les points de suspention suggèrent qu’on continue comme ca à l’infini. On a donc +inifini nombres. Maintenant on va regarder les mêmes en enlevant 0, il nous reste (1;2;3;…): on a toujours nos points de suspentions, donc on en a encore +infini, mais on en a enlevé 1, donc on en a +infini-1
donc +infini – 1 = +infini (ca c’est la version très simplifiée)
On peut remarquer que l’on passe sans problème du premier ensemble au deuxième en ajoutant 1, ainsi
01
12
23
etc…
En mettant à gauche un du 1e ensemble et à droite un du 2e. En faisant ca, on parcourt tout le premier ensemble et en même temps (même nombre d’étapes) tout le deuxième . Donc il y a bien autant de nombre, qu’il y en ai l’infini, ou l’infini moins 1.
Attention cependant, j’ai volontairement simplifié pour répondre, mais il y a plusieurs infinis de nombres, il y a un inifni beaucoup plus grand de nombres réels que de nombres entiers, mais ils gardent en commun de ne pas changer si on enleve un seul element
C’est même parfois comme cela que l’infini est défini: un ensemble est infini s’il est de même taille qu’une de ses parties strictes.
Vous avez une vision erronée de l’infini. La principale caractéristique de l’infini est d’être sans limite c’est-à-dire sans début ni fin. Par conséquent, dans un tel espace, pour toutes choses, il est impossible de demeurer, bien que les nombres le font par le biais d’abstractions mathématiques. Plus avant, quand j’écrivais que ∞=∞, cela ne vaut que pour l’espace non pour le temps qui, lui, possède bien un début et une fin. L’espace est aussi inamovible que le temps, impermanent.
Bien à vous…
je suis surpris que cette absurdité émeuve plus d’un. dans le calcul de notre « savant » il y a une hypothèse inavouée : la divergence de la série 1-1+1-1+1-… c’est au nom de cette divergence que quand il pose A=1-1+1-1+1-… = 1- A. Parce qu’en faite infini +/- a = infini (a nombre réel). en claire le savant étonné démontre la convergence d’une série après avoir supposé sa divergence.
Juste par curiosité : vous avez lu quelle fraction du billet avant de poster ce commentaire ?
vous dites en passant que la validitė de vos calculs est confirmée par la pratique en physique. c est, de très loin, le point le plus important. et le plus etonnant. pourquoi ne detaillez vous pas plus ce point? je ne trouve pas de reference à ce fameux « infini=-1/12 » (je simplifie, mais cela revient à ça, non?) dans mes maigres recherches sur l effet Casimir.
On peut voir ici une comparaison des différentes méthodes de calcul de l’effet Casimir :
http://www.maths.qmul.ac.uk/~tp/talks/casimir.pdf
Et notamment comment le -1/12 est lié à la formule d’Euler Mac-Laurin.
J’avais donné un peu plus de détails dans le dernier paragraphe de mon premier billet sur le sujet :
http://sciencetonnante.wordpress.com/2013/05/27/1234567-112/
(ce billet était moins rigoureux mathématiquement mais abordait plus les aspects physiques).
D’ailleurs si on regarde la formule d’Euler Mac-Laurin, voit que si on veut écrire une égalité du genre « infini=-1/12 », c’est plutôt :
$latex \int dx\ x – \sum_n n = -1/12$
merci pour votre réponse. et pour votre blog en général. Effectivement, l’application pratique était très bien développée dans votre premiere article. Je n’ai pas tous compris pour être honnete ( mais math niveau bac…). La formule d’Euler Mac Lauin me choque dèjà moins.
Pour les cas pratiques, je vois que c’est surtout utilisé en manipulant des dimensions multiples: je ne sais pas s il y a un rapport, mais finalement, une droite représente l ‘infini dans une dimension, et peut n’être qu’un point dans une dimension orthogonale.
Salut David,
Une petite question ouverte : je n’ai pas lu le raisonnement stricte, juste celui qui est approché et j’ai l’impression qu’on peut en faire un autre et trouver un résultat tout aussi raisonnable.
S=1+2+3+…
2S=2+4+6+…
2S-1=1+3+5+…
4S-1=1+2+3+4+5+6+…=S d’où S=1/3
Qu’est ce qui cloche là dedans et qui ne clochait pas dans la démo du billet précédent ? Quel argument rigoureux contredit ce résultat ? Est ce la « régularité, stablilité et linéarité » qui foire ?
Re-Salut ,
J’ai écrit n’importe quoi au-dessus, la troisième ligne est fausse. Donc, « avec les mains », on ne peut trouver que -1/12 ?
Effectivement je crois que tu as mis un 1 là où il y aurait dû avoir un A.
Malheureusement je n’ai pas de réponse à ta question :
* Le calcul que je présente au début pour trouver S ne respecte pas les 3 hypothèses « régularité, linéarité, stabilité », si tu regardes en détail, il y a une insertion d’un nombre infini de zéro à un endroit. Et pourtant il donne -1/12.
* Un autre calcul présenté plus loin dans le billet et respectant les 3 hypothèses aboutit à une contradition (0=1), donc par l’absurde on démontre qu’il ne peut pas exister de méthode respectant les 3 hypothèses et qui somme S.
* Les méthodes de la fonction zeta et de Ramanujan ne repsectent evidemment pas les 3 hypothèses, et pourtant donnent -1/12.
En conclusion, je n’ai aucune explication de pourquoi un calcul qui viole allégrement la linéarité donne quand même le bon résultat ! Coup de chance ? Signe d’un truc plus profond qui m’échappe ?
On peut imaginer montrer que la méthode zeta ne respecte pas la stabilité (insertion d’un nombre fini de zéro en tête) mais soit stable par l’insertion d’un nombre infini de zéro un terme sur 2 ?? Mais ça paraît tiré par les cheveux !
De manière générale, si on démontre que le calcul ‘heuristique’ n’utilise que des manipulations autorisées par la méthode de zeta, alors on démontre a posteriori sa validité. Mais je n’ai pas cherché.
Les points que j’avance ici se basent sur les résultats de ce document: https://arxiv.org/pdf/0705.1578v2.pdf
Pour répondre à David, oui le calcul peut être rendu rigoureux et c’est pourquoi il donne la bonne valeur et de la bonne façon. Mais malheureusement, il a quand même quelque chose d’arbitraire. Tout cela sera plus clair dans la suite.
La preuve de Matheux montre bien que la suite (1;2;3;4;…) n’est pas SSLSR, mais ça ne prouve absolument pas que les calculs heuristiques sont faux! Au contraire , ils sont en fait vrai. Et on peut les rendre parfaitement rigoureux en s’y prenant bien. La confusion vient du fait que (1;2;3;…) n’est pas SSLSR. Oui c’est vrai. Mais si vous le notez bien, dans le calcul, à aucun moment la stabilité n’est utilisée sur (1;2;3;…). L’erreur (de penser que c’est une erreur) vient du fait que comme on utilise la stabilité pour (1;-1;1;…) et (1;-2;3;-4;…), on pense forcément que l’opérateur doit aussi être stable pour (1;2;3;…), or ce n’est pas du tout nécessaire (et fort heureusement, parce que ça conduirait aux incohérences soulevées par Matheux).
Sisi, regardez bien le calcul, la seule propriété qui est utilisée pour (1;2;3;…) est la simplification de (0;1;0;2;0;3;0;…) à (1;2;3;…). Mézalor me direz-vous, comment justifier la rigueur de ce calcul? C’est là que le document nous fournit en partie la réponse. A la fin de la 3ème partie, il trouve que l’ensemble des suites polynomiales qu’on notera M (les suites P(n), n entier où P est un polynôme à coefficient complexe) est en somme directe avec les sommations maximales (qui existent par Zorn) (en gros). Notons qu’il appelle « sommation » une application linéaire et stable (à proprement parler une condition un peu plus faible que la stabilité).
Or justement, (1;2;3…) est une suite polynomiale (le polynôme est X+1). Donc pour définir une Suprasommation (une sommation encore plus grosse que celles qui sont maximales, car elle sera définie sur toutes les suites complexes), il suffit de considérer une sommation maximale (régulière de préférence…) qu’on appellera S1 de domaine H et de considérer une forme linéaire S2 sur M (facilement définissable, car on a une base algébrique évidente de M; par exemple les ((X+1)^k )(n); k parcourant les entiers naturels ). Cette Suprasommation S sera définie sur H+M (somme directe) = C^IN comme suit: Pour tout x dans C^IN, x s’écrit de manière unique x= y + P où y est dans H et P dans M et S(x)= S1(y) + S2(P).
On a bien une « somme » définie pour toute suite complexe car comme l’indique le Théorème 1.8 du doc, le soucis de non-sommation venait en fait des suites polynomiales. Celles-ci ne peuvent être compatibles avec la stabilité.
D’ailleurs, S1 est bien SSLSR mais pas S2.
Et pourtant, cela permet quand même de faire le calcul. Avec une telle définition, on a à priori toute une kyrielle de sommations possibles (déjà pour le choix de (S1;H) maximale mais aussi de S2…).
Et c’est là qu’intervient ce qui se cache derrière la simplification mystérieuse: Il existe une unique forme sur M qui est telle que S (quel que soit le choix de S1) soit invariante par la transformation ( P(n) ) ——-> ( 1/2*( 1-(-1)^n)*P((n-1)/2) ) (où autrement dit l’insertion d’un nombre infini de 0 une fois sur 2 en commençant par un 0 pour les suites polynomiales). Cela se démontre aisément par récurrence sur la base des ((X+1)^k)(n), k entiers naturels. Et en fait, toute sommation S= S1+S2, où S2 est la forme voulue, coïncidera avec la sommation de Dirichlet (limite quand s tend vers 0 de Somme des a_n/(n+1)^s) sur les suites polynomiales. A vrai dire, S2 = la sommation de Dirichlet en restriction aux suites polynomiales.
S1 est choisie – régulière si on veut (et sommant A=(1;-1;1;-1…) et B=(1;-2;3;-4;…) ), quoique la régularité n’est même pas nécessaire. Pourquoi ? Parce que A et B sont des séries quasi-exponentielles et n’importe quelle sommation (au sens du document) les sommant leur donne les valeurs trouvées par les calculs heuristiques. D’ailleurs, regardez de plus près ces calculs heuristiques. Vous verrez qu’on utilise à aucun moment la régularité…Le calcul prouve donc que quelle que soit la sommation sommant A (resp B) qui est stable et linéaire (seulement) alors telle valeur est donnée à A (resp B).
Donc S1 étant choisie (arbitrairement), je disais, il n’y a plus qu’une seule Suprasommation qui corresponde au calcul heuristique. Il suffit de prendre l’unique S2 vérifiant la propriété mentionnée plus haut.
Pour rappel, S(x) = S1(y) + S2(P), où x=y+P.
C’est parti pour le calcul!
S(A) = S1(A) = 1/2 car A appartient à H. S(B) = S1(B) = 1/4 car B appartient à H.
(A et B, en tant que séries quasi-exponentielles, appartiennent à n’importe quel H maximal ; Corollaire 3.6 du doc).
On a trouvé S1(B) = 1/4 car S1(B) = 1 – S1(B) – S1(A).
On note T = (1;2;3…) et T’ = (0;1;0;2;0;3;0;…).
On décide donc de sommer x = T – B.
S(x) = S( T – B) = S2(T) – S1(B), par unicité de la décomposition de x et linéarité de S1 (car T appartient à M et B appartient à H).
Mais x = 4T’, donc 4S(T’) = S(x) = S2(T) – S1(B).
Or comme on l’a dit, S2 a justement été choisie telle que S(T’) = S(T) (T est une suite polynomiale). Il vient donc 4S(T) = S(T) – 1/4. Soit S(T) = -1/12. CQFD
Et le calcul est parfaitement propre .
Alors évidemment, le choix de la forme sur M qui permet l‘invariance de S par insertion d’un 0 sur deux en commençant par un 0 sur les suites polynomiales parait arbitraire. Je suis d’accord. Rien tel quel dans la définition d’une somme, ne permet de savoir pourquoi ce serait cette forme-là particulièrement qui ferait mériter à S le titre de « généralisation » de la Somme. Mais on a bel et bien prouvé que le calcul est parfaitement licite et que, au moins dans un certain sens, 1+2+3+4+….= -1/12. Cependant pour peu qu’on choisisse les valeurs de S2 différemment (en posant des valeurs différentes aux éléments de la base de M), on obtient une autre forme linéaire S =S1+S2, où S1 est linéaire, stable (et régulière si on veut) qui en soi pourrait tout autant mériter le statut de « généralisation » de la notion de somme mais donnerait une valeur différente à (1;2;3;4;….).
Ainsi le choix des valeurs de S2 sur une base de M détermine quelle sommation (et donc quelle valeur) on obtiendra pour toute suite qui contient une partie polynomiale.
Alors petite précision à propos de ce que je dis juste au dessus. Sur deux points.
Déjà le premier est que, pour être valide, le calcul n’a même pas besoin de supposer une propriété aussi forte que celle que j’ai mise (la simplification des 0 qui sont distribué une fois sur deux en débutant par un 0, cette simplification étant valide pour toutes les suites polynomiales). En fait, dans l’absolu, la véracité du calcul de David peut être légitimée simplement en supposant que cette simplification peut se faire pour la suite (0;1;0;2;0;3;0;4;0;5;0;….), ce qui donnera pour valeur -1/12. Mais supposer juste que l’opérateur se simplifie pour cette suite-là semble un tantinet artificiel. Quoiqu’il en soit, c’est mathématiquement juste. La valeur d’une telle somme (comme définie dans le précédent commentaire) sur la suite des entiers vaut -1/12 si et seulement elle peut se simplifier de S(0;1;0;2;0;3;0;4;0;5;0;….) à S(1;2;3;4;5;…); puisqu’on a justement la relation (qui vaut quel que soit la somme S):
4S(0;1;0;2;0;3;0;4;0;5;0;….) = S(1;2;3;4;5;…) – 1/4.
Le deuxième point, rejoignant le premier, est que je disais que rien ne légitime plus cette forme là ( la forme S2 définie sur les suites polynomiales et vérifiant la propriété d’invariance pour toutes ces suites) comme étant la généralisation de la somme. Or, justement, il me semble qu’une caractéristique raisonnable attendue d’une « somme » serait justement une invariance par insertion de 0 de ce type (oui je reconnais que même à supposer cela, ce ne serait pas la seule légitime). Pourquoi je dis ça? Bah la convergence classique des séries est invariante par insertion quelconque de 0 (en nombre fini ou infini). Et on a séparé notre espace C^IN en la somme directe H+M. Or l’opérateur S est invariant par insertion d’un 0 en tête de suite pour H. Il me parait donc « raisonnable » et « légitime » d’exiger une certaine propriété d’invariance (par insertion de 0) pour l’espace M.
Pourquoi nécessairement celle que j’ai présentée? Je n’en sais absolument rien, mais c’est l’idée. Evidemment ce dernier point n’est qu’encore que trop subjectif. Chacun peut émettre son avis sur les propriétés à choisir pour parler de « Somme » avec un grand S (comprendre définie sur l’espace entier des suites complexes). Mais, on a quand même bien avancé non? 😉
A la rigueur, il faudrait peut être plus étudier cette forme S2 pour en faire apparaître des caractéristiques qui la rendraient encore plus « légitime ». Wait and see…
La méthode heuristique utilise une autre propriété que régularité, linéarité et stabilité.
Reprenons la fin de la démonstration :
S – B = (1 + 2 + 3 + 4 + 5 + 6 + 7 + … ) – (1 – 2 + 3 – 4 + 5 – 6 + 7 + …) = (0 + 4 + 0 + 8 + 0 + 12 + 0 + …)
A ce stade de la démonstration, ilretire les 0 de la somme, alors que ni la régularité, ni la linéarité, ni la stabilité ne le permettent.
Ce retrait de 0 peut sembler anodin ; cependant, si nous reprenons les moyennes de Césaro et que nous considérons la somme suivante :
A’ = 1 + 0 – 1 + 1 + 0 – 1 + 1 + 0 – 1 + …
Je n’ai fait qu’ajouter des 0 dans la somme A ; et pourtant, il est facile de se convaincre que la somme en moyenne de Césaro vaut 2/3 et non 1/2.
À priori la linéarité et la stabilité ne semblent pas le permettre. Mais il se trouve que sous certaines c’est en fait le cas. Mais uniquement avec le un terme sur deux est un zéro.
Tu peux t’en convaincre avec Césaro et Abel par exemple. Si tu dilue ta suite (insérer des 0) de façon à avoir un 0 sur 2, alors on préserve la sommabilité et on a même valeur de somme.
Ton exemple est un autre type de dilution. Le résultat que je mentionne fonctionne avec la dilution des manio heuristiques et quelques autres dilutions, mais pas toutes…;)
Pingback: La série qui tend vers moins un douxième, étrangement | Blog de tcit
(infini) = 2 * (infini) +1
0 = infini +1
infini = -1
Ah tiens, pas bête. Je m’en étais jamais rendu compte…
Un peu risqué ! Thesacristan va-t-il persevoir l’ironie de ta réponse ?
Bonjour,
Je me pose quelques questions quand même. Par exemple celles-ci :
1) l’addition (de 2 entiers en tous cas, et par récurrence d’un nombre quelconque d’entiers) est en principe une loi de composition interne. Comment se fait-il que l’addition d’un nombre infini d’entiers perd cette propriété d’être une loi de composition interne, puisque le résultat n’est pas un entier ?
2) est-ce que Cantor n’a rien fait à ce sujet ?
3) qu’en pense l’analyse non-standard (Robinson, Nelson, Reeb…) ?
Je ne sais pas ce qu’est Cantor ni l’analyse son-standard. Je me permets juste de répondre à votre première question (aussi vieille soit-elle… Je viens de tomber dessus) :
L’addition dont on parle quand on écrit 1+2+3+…=-1/12 n’est pas une addition. C’est une forme linéaire de R^N dans R, c’est-à-dire une fonction qui prend une suite infinie de réels et leur associe un nombre réel. En fait, on devrait écrire : f(1,2,3,4…) = -1/12. C’est d’ailleurs pour cela que l’on perd la commutativité.
Ici, on a choisit l’écriture 1+2+3+… plutôt que f(1,2,3,…) parce que, pour tout n de N, f(a0,a1,…an) = a0+a1+…+an pour tout vecteur (a0,a1,…,an) de R^n. Autrement dit, si on prenait n nombres réels quelconques, l’image de ces n nombres par f serait leur somme. C’est pour cela qu’on dit parfois qu’on a « étendu la définition de l’addition », même si c’est une très mauvaise formulation je trouve.
Merci pour ce très bon billet !
En effet ce sujet fait le big buzz …
http://www.nytimes.com/2014/02/04/science/in-the-end-it-all-adds-up-to.html
http://plus.maths.org/content/infinity-or-just-112
Il y a eu une excellente conférence en ligne donnée en 2009 par le mathématicien Jean-Pierre Ramis – « Leonhard Euler, ou l’art de donner un sens à ce qui n’en avait pas ». http://vimeo.com/30907930
Et le livre de synthèse lisible par les lecteurs de cette rubrique: J.-P. RAMIS
Séries divergentes et théories asymptotiques
Panoramas et Synthèses, Société mathématique de France (1993)
Je vous signale aussi l’article de Jérôme Buzzi Liberté et formalisme : 1+2+3+4+5+… = ? http://images.math.cnrs.fr/Liberte-et-formalisme-1-2-3-4-5.html paru le 17 février 2014 sur Image des maths.
je suis tombé sur cet article un peu par hasard et après l’avoir lu, j’aimerai vous posez une question (au risque de paraitre stupide ^^) : comment avez vous décomposé le terme entre parenthèses dans l’exemple 2 (somme B) ?
Pingback: La série qui tend vers moins un douxième, étrangement | Blog de tcit
(QUÉBEC) Étant personnellement seulement rendu en secondaire 5 (dernière année avant le CÉGEP, j’ai 16 ans), je n’ai vraiment pas tout compris malgré que j’aie tout lu! 😉 Je me demandais, est-ce que ça signifie que INFINI = -1/12 ? Je vous lis depuis que j’ai lu un de vos articles sur Flipboard et je suis tombé en amour avec votre site. Très intéressant, continuez de m’épater. J’ai particulièrement été fasciné par 0,999… = 1!
Très intéressant tout cela. Pas évident de tout comprendre. une question : Si l’on considère la somme des entiers naturels (1+2+3+4+5+6+…) comme la somme des entiers naturels impairs plus la somme des entiers naturels pairs, utilise-t-on la commutativité? Et si oui la suite des calculs n’est pas »valable » étant donné qu’on est en présence de sommes infinies.
en faisant cette manip et en reprenant le genre de calculs heuristiques exposés dans l’article je tombe sur 1+2+3+4+5+6+7+… = -1/6.
Oui c’est exact. Séparer les termes pairs et impairs implique d’utiliser violemment la commutativité (un nombre infini de commutations même !), et donc on sort de la règle de linéarité. On peut donc se retrouver avec n’importe quoi.
Merci pour cet éclairage. Donc on aurait pas plus n’importe quoi que -1/12, à la différence qu’on retrouve -1/12 avec d’autres méthodes. Dans les calculs exposés au début de l’article, la règle de linéarité n’est pas respectée non plus ?
Les deux premiers calculs respectent les 3 conditions (linéarité, régularité, stabilité), le résultat qu’elles donnent est donc en un sens le seul raisonnable.
En revanche le 3ème calcul ne respecte effectivement pas la linéarité. Dans les commentaires, quelqu’un a montré que pour la somme 1+2+3+4+5+…, il ne pouvait pas y avoir de méthode respectant les 3 conditions (démo par l’absurde : en appliquant les 3 conditions on peut tomber sur des résultats différents).
Merci pour la réponse. Effectivement il me semblait bien avoir compris cela au vu des commentaires. et merci pour cette page qui amène du sens et du fond à ce résultat que l’on trouve ça et là sur le net.
La somme B est soit égale à -N/2 si N est paire soit (N+1)/2 si N est impaire. L’infinie dans ce cas prend une valeur paire ou impaire. Par contre la moyenne entre -N/2 et (N+1)/2 est justement 1/4. Il ne faut pas confondre convergence et égalité. La question est pourquoi la valeur moyenne.
« Convergence » (plus précisément « convergence vers ») fait sens pour moi. « Je ne vois pas ce que vous voulez dire par « égalité ». Pourquoi la moyenne? Parce que si on prend une autre méthode de convergence « raisonnable » on obtiendra le même résultat.
Bonjour,
Vos deux billets étant tous deux très intéressants je me permets d’y participer, ou plutôt devrais-je dire, de venir vous interroger quant à deux points qui me turlupinent plus qu’autre chose. Mon niveau de Math est celui d’un post-prépa scientifique donc je connais assez bien les séries mais je n’ai jamais trop étudié les séries divergentes ( d’où je pense mon incompréhension ).
Dès le début, le résultat de A m’intrigue.
En effet, A = 1 – 1 + 1 – 1 + 1 … , ce qu’on peut donc regrouper sous la forme de E(-1)^n ( E étant le signe somme ) pour n = 0 jusqu’à l’infini ?
Mais pour arriver à prouver que A = 1/2 , vous affirmez qu’on peut séparer le terme n=0 du reste et conclure que le reste est à nouveau A. Cela revient à dire que E(-1)^n = E(-1)^k , où n=0 => infini et k=1 => infini ?
Or je trouve cela très déroutant de pouvoir considérer, et ce même pour une suite de termes infinie que l’on peut soustraire, 1 ou même X termes à celle-ci et affirmer que le résultat est identique ( sachant que le résultat dont je parle n’existe pas vraiment du fait de leur infinité ).
D’après votre billet c’est possible selon la méthode de Césaro ( que je découvre avec votre billet ), mais, si j’ai bien compris son fonctionnement, on va ici sommer les sommes partielles de A ( à savoir SA0 + SA1 etc.. ) où SA0 = 1 / SA1 = 1 – 1 / SA2 = 1 – 1 + 1 / etc.. ) Mais donc ici encore une fois, ce même soucis d’alternance infinie se présente ? et la multiplication par 1/n ( avec n => infini ) ne peut aboutir à un résultat fixe de 1/2 ? Je pense que c’est ici que je bloque concrètement.
Pour ce qui est d’Abel, de la fonction Zeta de Riemann et de Ramanujan j’avoue ne pas réellement saisir, mais je pense qu’une fois ce coin sombre éclaircit, ne serait-ce qu’au niveau de la série A je serai en mesure de mieux appréhender ( à ma hauteur en tout cas ) le reste de ce fantastique billet.
Merci beaucoup.
Je me permets de vous recommander l’excellente conférence de Jean-Pierre Ramis http://vimeo.com/30907930 qui éclairera peut-être votre lanterne.
J’ajoute mon commentaire sous forme de deux questions liées à celle que je posais plus haut:
* Que signifie «identique» dans «affirmer que le résultat est identique»?
* Que signifie «existe» dans «le résultat … n’existe pas vraiment du fait de leur infinité »?
Ce que dit Euler est déroutant parce qu’il nous impose à préciser le sens des termes comme «convergence», «égalité», «identité», «existence», quitte à en étendre le sens habituel tout en restant cohérent.
(-: Merci Leonhard tu nous fais réfléchir!
En utilisant ce type de calcul (qui suppose par exemple que 1-1+1…existe) on démontre que 1=2 et autres résultats convaincants. Cela signifie que le nombre n’existe pas, alors qu’on suppose le contraire. Quand à la fonction dzeta, elle illustre simplement que la limite de la série n’est pas la série des limites (sauf, justement, si celle-ci converge). J’aime bien les arguments sur la théorie des cordes, qui promet tout et ne fait rien, qui donne des résultats faux sur plusieurs centaines d’ordres de grandeur (!), qui contient une infinité de théories…J’aime aussi l’argument: une somme ne peut être infinie dans notre univers donc c’est normal. C’est assez pitoyable. 1=2: bravo!
Je pose ici une question similaire aux questions précédentes:
* Que signifie « 1-1+1…existe » ?
La théorie des séries divergentes n’affirme pas que la série 1-1+1.. converge, mais que l’on peut de façon cohérente lui associer une somme, ce qui n’est pas la même chose. Dans une théorie mathématique cohérente (ou consistante) on ne peut pas démontrer que 1=2. Donc tout va bien! 🙂
Très bon billet , avec une mise au point clair sur les séries divergentes et l’infini : la citation finale d’Abel résume tout ! 🙂
Bonjour à tous !
J’ai l’impression qu’il y a un soucis dès le départ du raisonnement. Je m’explique :
Prenons la suite A[sub]n+1[/sub] = 1 – A[sub]n[/sub] avec A[sub]0[/sub] = 0
A[sub]1[/sub] = 1 – A[sub]0[/sub] = 1 – 0 = 1
A[sub]2[/sub] = 1 – A[sub]1[/sub] = 1 – 1 = 0
A[sub]3[/sub] = 1 – A[sub]2[/sub] = 1 – (1 – A[sub]1[/sub]) = 1 – (1 -1) = 1 – 1 + 1 = 1
A[sub]4[/sub] = 1 – A[sub]3[/sub] = 1 – (1 – 1 + 1) = 1 – 1 + 1 – 1 = 0
A[sub]5[/sub] = 1 – A[sub]4[/sub] = 1 – (1 – 1 +1 – 1) = 1 -1 +1 -1 +1 = 1
…
A[sub]n[/sub] = 1 – 1 + 1 -1 +1 -1 + …….
Nous sommes tous d’accord que si A[sub]n[/sub] = 0 alors A[sub]n+1[/sub] = 1 – [sub]n[/sub] = 1 – 0 = 1,
et que si A[sub]n[/sub] = 1 alors A[sub]n+1[/sub] = 1 – A[sub]n[/sub] = 1 -1 = 0
Dans le raisonnement nous avons A = 1 -1 +1 -1 +1 …… avec un nombre infini de termes, donc A = A[sub]n[/sub] avec n qui est égal à l’infini.
Donc dire que A = 1 – A, revient à dire que A[sub]n[/sub] = 1 – A[sub]n[/sub] = A[sub]n+1[/sub] , donc que 1 = 0.
Je dirai donc que A semble égal à 1 – A, mais ce n’est pas pour autant qu’il l’est. On peut certes me dire qu’A[sub]n[/sub] converge vers 1/2 lorsque n tend vers l’infini, mais le résultat est là. Dire que A = 1 – A revient à dire que lorsqu’on atteint l’infini (ce qui est normalement impossible), 0 = 1.
Après je peux me tromper, mais ça voudrait dire que tout ce que j’ai appris jusqu’ici en mathématiques est faux, et ça m’ennuierai un peu.
Hum…… quelqu’un peut m’expliquer comment mettre en indice ici ? Merci d’avance.
…et accessoirement comment on fait pour éditer…
Pingback: Une somme « absurde »: 1+2+3+4+…=-1/12 | Bric-à-brac mathématique
Imaginons un théorème : deux nombres sont égaux si on ne peut intercaler un autre nombre entre les deux = Vrai
Donc 0,999999…. = 1 = 1,000000……..1
Sauf que 0,999999…. ne reste pas égal à 1,00000…1
Hors je trouve que dans cet argumentaire vous rapprochez deux valeurs qui n’ont strictement rien à voir :
1+2+3+4+5… = infini, qui peut donc être égal à -1/12
Mais on ne peut pas rapprocher les deux valeurs.
De plus, 1+2+3… est obligatoirement positif, alors que -1/12 est négatif…
Le titre est donc selon moi de base mensonger.
Par exemple :
x = 0,999…
10x = 9,999…
10x = 9+x
10x-x = 9+x-x
9x = 9
x = 9 ÷ 9
x = 1
Là encore malgré tout je ne suis pas d’accord avec cette équation car un nombre est infini et l’autre fini, ce qui est une nouvelle fois en contradiction…
Je pense que 0,999… est bien égal à 1. En effet si ne n’était pas le cas, appelons epsilon la différence des 2 nombres. On peut montrer que quelque soit epsilon il existe une écriture partielle de 0,99… dont la différence avec 1 est plus petite que epsilon. Donc il ne peut exister d’epsilon>0 qui soit la différence des 2 nombres. Donc epsilon = 0, soit 0,9999…. = 1
Ça fait bien longtemps que je n’ai pas fait de maths, j’espère que mon raisonnement est bon.
Il y a une erreur dans votre égalité 1=1,000000….1
Le nombre de droit est fini, contrairement à ce que les points laissent entendre. Le nombre de zéros avant le 1 final peut être très grand mais au final ceci représente un nombre fini.
L écart avec 1 est 0,00000….1
0.999999… = 1 est une vérité en mathématique, quoi que vous puissiez en penser. Mais c’est là qu’on voit le coeur du problème : qu’est-ce que 0.9999… ? Et que veut dire =1 ? Tout ce qu’on dit ici en fait, c’est que la somme infinie des 9*10^-n converge vers 1. Rien de plus. 0.99999… n’est pas un nombre puisque « … » n’est pas une décimale et n’a pas de vrai définition en soi.
Pingback: L’effet Casimir…et le retour de 1+2+3+4+5+…=-1/12 ! | Science étonnante
Si on trouve 2 méthodes régulières, linéaires et stables pour sommer une série divergente au sens classique, les 2 méthodes vont elles donner le même résultat ?
Bonjour,
Juste pour dire que quand vous dites « si on change l’ordre des termes dans l’addition, on peut changer la valeur de la limite », ca aurait bien de montrer et expliquer sur un exemple, afin qu’on puisse voir comment on peut changer l’ordre des termes dans une addition d’une infinité de terme, cela m’a laissé un peu sur ma fin.
En fait je crois que dans tout cet article, on ne voit pas une seule fois deux façons différentes de sommer une suite infinie de termes et donnant des résultats convergents différents. C’est dommage, un exemple concret devrait permettrait peut-être d’y voir plus clair.
Intéressant de voir enfin quelqu’un entrer un peu dans les détails de ce résultat.
Je me permets de répondre aux questions que vous posez dans votre post :
1) C’est la stabilité qui n’est pas respectée dans votre exemple 0=1. En effet, les méthodes de sommation utilisées ne sont pas stables, et ainsi, les 3 expressions de S que vous donnez ne sont pas égales. Je peux donner plus de détail si nécessaire, mais la simple définition des série de Dirichlet et de la stabilité devraient répondre à la question.
2) 1+2+3+…=-1/12 n’a jamais été validé par la physique comme on veut le faire croire. Les physiciens utilisent en fait le résultat : \left(\sum_n n – \int x\ dx\right) = – 1/12 dans le cadre d’un calcul relatif. Autrement dit, on a 1+2+3+… = l’infini – 1/12. Seulement, dans l’effet Casimir, ce résultat est utilisé dans le cas d’une différence de potentiel. Le calcul de cette différence permet de se débarrasser du terme infini. Dans le calcul de la Force de Casimir, cette fois, une dérivée permet de se débarrasser du terme gênant. Quoi qu’il en soit, dire que 1+2+3+… = -1/12, c’est comme dire que Epotentielle = mgh. C’est vrai, mais uniquement dans un certain référentiel.
En relisant votre post, je m’aperçois que j’ai mal compris vos interrogations.
1) La démonstration permettant d’aboutir à 1+2+3+… = zeta(-1) utilise la représentation en série de Dirichlet qui n’est pas stable. D’ailleurs, ça ne pourrait absolument pas être la linéarité qui ne soit pas respectée. Sinon, l’écriture même 1+2+3… serait absurde.
2) En utilisant la linéarité, l’unicité du prolongement analytique et l’identité sur les espaces où les suites convergent (on doit par exemple toujours avoir f(Uk1,Uk2,…,Ukp) = Uk1+Uk2+…+Ukp), on peut montrer que tout procédé de sommation linéaire qui permet de sommer (Un) donnerait le même résultat.
J’aimerais dire quand même que quand on présente un article sur un sujet aussi bizarre que « la somme des entiers vaut -1/12 » il faut définir les choses. C’est comme si je disais 0 est une matrice, tout le monde me dira « non tu as oublié les parenthèses » et j’écris un autre article en blâmant ces personnes et en disant que c’est une notation pour la matrice nulle. C’est le même principe, même si il est moins « cool ».
Le grand Euler n’avait pas plus défini les choses quand il avait introduit le sujet, mais ça n’est pas une excuse. Il faut définir les choses autant que quand on dit qu’il n’y a pas de somme des entiers ou quand on dit que la somme des inverses des carrés des entiers vaut ᴨ²/6. Il s’agit dans tous les cas de vulgariser des mathématiques.
Bonjour, je ne comprend toujours pas comment vous passez de A = 1-1+1-1+1-1
à A = 1 – A
Si nous cherchons une formalisation de la suite, il s’ensuit une divergence évidente.
Si je cherche à comprendre cette suite, j’y vois : à chaque fois que l’on ajoute 1, on y retire 1, et à chaque fois que nous retirons 1, nous rajoutons 1.
Dans votre exemple, 1-A n’est pas égale à A.
Plutôt, 1 – 1 + A = A ce qui semble beaucoup plus correct, n’est-ce pas ?
Toute la question reste de savoir quand A se termine (sur -1 ou sur 1) Et comme la suite n’indique pas d’arrêt, c’est autre chose…
La série diverge si on l’entend comme sa définition classique : Somme de 0 à +l’infini des (-1)^n. Mais que se passe-t-il si on la considère comme la limite quand x tend vers 1 de la somme des (-x)^n ? On peut trouver de nombreuses autres façons de définir A comme la limite d’une série de fonction, et dans certains cas, la somme des limites diverges, mais pas la limite de la somme. Tout est une question de définition…
Je vais tenter de donner une justification (assez) rigoureuse des calculs aboutissant à la somme
1 + 2 + 3 + … = -1/12.
Pour cela, je vais m’intéresser à la série formelle :
F(x) = Σ n x^n
et à la série formelle dérivée
F(x²) = Σ p x^(2p).
Considérons aussi la série formelle :
1/(1+x)² = Σ (-1)^n n x^n.
Ces trois séries formelles satisfont l’égalité (qui ne fait pas référence à la convergence) :
1/(1+x)² + 4 F(x²) = F(x).
soit
F(x) – 4 F(x²) = 1/(1+x)².
Par passage à la limite, F(1) « est » la somme Σ n et ce passage à la limite peut être justifiée mathématiquement. Or d’après l’égalité ci-dessus,
F(1) – 4 F(1) = 1 / 4,
d’où
F(1) = Σ n = -1/12.
Pingback: Additionner des entiers, 2ème partie : les séries divergentes – Mathomate
On en est où ?
Si je résume bien, on a une théorie mathématique qui affecte une valeur aux séries divergentes, qui coïnciderait avec des observations physiques. Cependant, cette théorie est incomplète, il doit manquer des restrictions/conditions car elle donne aussi des résultats faux.
La théorie s’est-elle affinée ?
On m’avait présenté ces calculs il y a quelques temps et je m’étais amusé à faire quelques calculs pour tuer cette théorie. C’était avant de lire votre blog. Voici mes calculs :
Je nomme :
U = 1+1+1+1+1+…
D = 2+2+2+2+2+…
P = 2+4+6+8+10+…
I = 1+3+5+7+9+…
On a P+U=1+I et I+U=P, en additionnant ces deux égalités je trouve U=1/2
Jusque là c’est bon ?
Puis D=2U donc D=1
Mais aussi D+P=2+P qui conduit à D=2
Je trouve donc D=1=2 Absurde !
Au passage en utilisant S=P+I je trouve I=-7/24 et P=5/24 …
Ça m’intéresse beaucoup tout ça, il faudrait juste trouver ce qui est légal et ce qui ne l’est pas afin d’avoir quelque chose de « consistant » sans quoi on ne peut pas calculer les autres séries divergentes hormis celle qui a trouvé une « validation » expérimentale !
Pardon erreurs de signe mais ça ne change pas grand chose, je corrige :
1+P+U=I et I=P-U conduit à U=-1/2
Et ensuite 2+D+P=P conduit à D=-2 contradictoire avec D=2U=-1
Avez-vous lu http://images.math.cnrs.fr/Liberte-et-formalisme-1-2-3-4-5.html et regardé https://vimeo.com/30907930 ?
Il me semble que pour les séries alternées on peut utiliser effectivement des sommations trigonométriques et la régularité est alors trigonométrique… La sommation de Ramanujan n’est pas une sommation trigonométrique… mais une sommation logarithmique…
et la régularité est alors logarithmique…
jaimerais bien comprendre le demonstration de la premiere somme. A= 1-1+1-1+1-1+1….
cette est égale a 1 ou 0 si le nombre de terme est pair ou impair
En gros,si tu définis la somme A = limite quand x tend vers 1 de la limite quand n tend vers l’infini de la somme des (-x)^n, tu as :
– somme des termes d’une suite géométrique de raison x => somme des (-x)^n = (1-(-x)^n)/(1+x)
– limite quand n tend vers l’infini avec |x| limite quand n tend vers l’infini de la somme des (-x)^n = 1/(1+x)
– limite quand x tend vers 1 du tout = 1/2
Il y a un eu un problème avec mon message.
– limite quand n tend vers l’infini avec |x| limite quand n tend vers l’infini de la somme des (-x)^n = 1/(1+x)
à remplacer par :
– limite quand n tend vers l’infini avec |x|<1 de la somme des (-x)^n = 1/(1+x)
Sans définition rigoureuse on peut dire n’importe quoi. Je vais donc essayer de faire ce que vous ne faites pas (car ça vous arrange 🙂 )
Je note S l’espace vectoriel sur R des suites de réels. Je note C le sous espace des suites qui convergent au sens usuel et je note l(x) la limite usuelle d’une suite x de C. l est une forme linéaire sur C. Supposons qu’on dispose d’une forme linaire l’ qui prolonge l sur S et qui soit invariante par translation à gauche (ce qu’on attend de toute notion de limite, c’est qu’en supprimant le premier terme, on obtienne la même limite. C’est vérifié d’ailleurs par la notion de limite au sens de Césaro dont vous parlez). Je note s(x) la suite x décalée d’un cran à gauche.
Alors pour un tel prolongement l’ voici ce qu’il donnerait pour la suite Tn=1+…+n :
On a d’une part l'(T+s(T))=l'(T)+l'(s(T))=l'(T)+l'(T)=2l'(T) et d’autre part l'(T+s(T))=l'(2T_1+2,2T_2+3,….)=2l'(T+s(T))=2l'(T)+l'(s(T))=3l'(T). Donc l'(T)=0.
Autrement dit si une notion acceptable de limite existait pour donner un sens à ce que vous faites, la valeur de la limite serait 0.
Bref, la notion de limite que vous voulez évoquez n’est soit pas linéaire, soit pas invariante par translation à gauche. Dans tous les cas, cela n’est donc pas une extension de la notion de limite même avec un esprit extrêmement ouvert !
Enfin, dans votre premier calcul, pourquoi n’écrivez vous pas que A=(1-1)+(1-1)+(1-1)+…=0+0+0+…=0 ? Après tout, c’est tout aussi faux que le calcul que vous faites, donc pourquoi pas choisir 0 comme valeur pour A si ce n’est pour aboutir à des conclusions rigolotes mais absolument pas rigoureuses (car non définies) ?
Merci pour votre blog qui contribue, malgré son contenu très peu mathématique, à aiguiser les cerveaux grâce au bon choix du buzz.
PS
Quant à la justification physique (gloups !!!) que vous pensez détenir, elle ne justifie pas votre calcul (où vous réordonnez les termes dans un ordre qui vous arrange mais qui pourrait être tout autre). Simplement, elle est liée au fait que le calcul physique lié au modèle oscillatoire fait la moyenné via Césaro d’un certain arrangement et amène donc vraiment à -1/12. Ce qui est fait dans votre blog c’est de faire croire que les deux écritures après réarrangement des termes sont égaux (alors que ce réarrangement est contradictoire).
Il n’y a donc malheureusement aucun mystère, aucun paradoxe ni aucune justification physique de vos erreurs d’arrangements de sommation.
Billet et réponses très fascinants.
Toujours, ce qui convainc n’est pas la finesse ou l’exactitude de ses propos, mais le ton de certitude avec lequel on les affirme. Cher David, certains de vos lecteurs vous contredisent sans grande modestie, mais avec un ton de grande certitude atteignant la moquerie: ils doivent donc avoir sans doute raison. Je l’affirme avec un ton de grande certitude, bien sûr 🙂
Merci beaucoup pour votre blog.
Oui vous avez raison. Il faut toujours garder en tête le livre de Shopenaueur « L’Art d’avoir toujours raison » https://fr.wikisource.org/wiki/L%E2%80%99Art_d%E2%80%99avoir_toujours_raison Quoique beaucoup de stratagèmes soient utilisés, il me semble que ceux qui nient la rigueur mathématique sous-jacente à ce qu’aucuns appellent les séries divergentes ont une préférence pour le stratagème XIV. Peut-être appliquent-ils le stratagème XXXI?
Merci aussi pour le blog.
A reblogué ceci sur Curation exclusivement en français.
Comme tous j’ai été intrigué par ces calculs étonnants qui prétendent que S=-1/12!
Je suis bien entendu d’accord avec Jean Pierre Morvan.
Le premier calcul de A = 1 -1 +1 -1 +1 -1 +… doit prendre en compte le nombre de termes de la somme.
Si A est constitué de n termes alternés alors on écrit
A(n) = 1 -1 +1 -1 +1 -1 +… puis on pose A(n) = 1 – (1 -1 +1 -1 +1 -1 +… ) = 1 – A(n-1) eq. 1
Dans ce cas A(n) n’est pas égal A(n-1) puisque A(n) a un terme de plus et l’équation A = 1 – A est fausse.
A vaut donc soit 1 pour n impair soit 0 pour n pair, comme le dit Jean Pierre.
De même pour le calcul de B, en tenant compte du nombre de termes mis en jeu, on trouve facilement que:
B(n) = 1 – B(n-1) – A(n-1) qui se transforme en considérant la parité de n, en:
si n est impair, et tenant compte de l’eq. 1
B(n) = 2 – B(n-1) – A(n) avec A(n)= 1, et donc B(n) = 1 – B(n-1) eq. 2
mais par définition B(n) = B(n-1) + n eq. 3
d’où B(n) = (n+1)/2
et si n est pair,
B(n) = – B(n-1) – A(n) mais dans ce cas A(n)= 0, et donc B(n) = -B(n-1) eq. 4
puis en utilisant l’eq. 3 on obtient B(n) = – n / 2.
(Ok avec Jean Pierre)
Maintenant revenons au calcul de S(n):
En comptabilisant précisément le nombre de termes dans ces équations on peut obtenir
S(n) – B(n) = 4. S(n/2) pour n pair ou bien S(n) – B(n) = 4 . S[(n-1)/2] pour n impair
Et bien sûr en aucun cas on ne peut écrire que S(n) = S(n/2) ni égal à S[(n-1)/2] (en effet le second terme de l’égalité contient 2 fois moins de termes que le premier: dans ce cas l’approximation est aussi farfelue que de dire la somme des termes de 1 à n/2 est égale à la somme de termes de n/2 à n) !
Pour terminer, 1 + 2 + 3 + 4 + 5 + … + n = n.(n+1) / 2 et donc quand n tend vers l’infini, S aussi.
Alain Bensoussan.
Honnêtement et très respectueusement, M. Alain Bensoussan vous ne pouvez pas avoir le billet en entier, réfléchir et rédiger ce commentaire…si?
avoir lu*
Merci Manu. Non effectivement je n’ai pas pris le temps de tout lire mais j’ai voulu partager mes réflexions avec vous tous. Ce blog que je viens de découvrir est très bien. Bravo à David Louapre et à tous.
Rdv peut-être sur la discussion sur les nombres premiers et la conjecture de Goldbach (suite à la suggestion de Jean Pierre.
(Nota c’est plus sympa de s’appeler par son prénom que de mettre monsieur, non ?). Vu mon emploi du temps en semaine il est possible que je ne puisse intervenir de façon assidue,
Alain
C’est vraiment dommage. Parce qu’en plus d’être respectueux pour le dur travail fait par David, avoir lu l’article vous aurait évité de plussoyer des commentaires ‘inutilement offensant envers son article’ (comprendre: dont la pertinence tend vers zéro; « tend vers », comprendre: « est exactement de »).
Vous passez à côté d’un pan des Mathématiques solide et (très) intéressant sans même vous en rendre compte, alors que vous devriez avoir les connaissances pour le comprendre. L’article est, certes, très perfectible, mais on est à un tout autre niveau qu’une histoire de « nombre de termes de la somme »!
Sans même lire l’article, ni réfléchir au sens des notions abordées, rien qu’en lisant les inter-titres, on comprend que votre contradiction ne tient absolument pas debout. Je cite:
– Rappel des faits
– Comment sommer un nombre infini de termes ?
– La méthode « naturelle »
– Bye bye la commutativité !
– D’autres méthodes de sommation ?
– La méthode de Cesaro
– La méthode d’Abel
– Stabilité, linéarité, régularité
– La régularisation par la fonction zeta
– Quelques questions ouvertes (pour moi)
Je retire ce que j’ai dit…dès le troisième intertitre (voir le deuxième, je vous l’accorde), on comprend que c’est un peu plus subtil que ça. C’est vraiment dommage de se permettre d’émettre une critique/opinion dans ces conditions. Pour donner de l’eau au moulin de Jean-Pierre en plus…
Vous savez le nombre de mathématiciens qui ont publié et travaillé sur cette question? L’argument d’autorité n’est certainement pas une preuve en soi; mais quand même! D’un côté on a de purs génies qui publient des choses qui sont l’oeuvre d’une vie, appuyées par d’autres au fil des décennies et de l’autre des personnes informées de la lecture d’un blog lu en diagonal (je n’ai pas trouvé de mots pour illustrer une superficialité plus forte) en à tout casser 35 secondes (c’est le temps qu’il m’a fallu pour lire le premier intertitre, faire défiler le curseur de ma souris, lire le deuxième, encore faire défiler le curseur de ma souris, commencer à lire le troisième, arrêter par flemme…donc j’imagine que pour vous ça a même dû même être moins que ça)….un peu de sérieux!
En espérant que ce message vous aura fait réagir positivement. Très sincèrement, Bonne Lecture.
J’ai déjà remercié David pour l’article et sorti mes griffes pour en défendre la légitimité ainsi que la qualité. Donc je me permets d’aller droit au but par quelques remarques sur les points qui auraient pu être (un tout petit peu) plus rigoureux.
Un point de détail pèche sur la stabilité. la définition « sortir un nombre fini de zéro » ne suffit pas semble-t-il. Il faudrait également préciser qu’on peut en rentrer un nombre fini. Parce que tel quel, rien ne permet, sans cette précision, de faire l’opération dans l’autre sens (à moins que l’on montre qu’il suffit de l’avoir dans un sens pour l’avoir dans l’autre; ce que je n’ai pas su faire). Le sens est respecté dans le calcul heuristique, mais pas dans la preuve de Matheux.
Rigoureusement, il aurait fallu supposer qu’il existe une SSSLR (Super Sommation Stable Linéaire et régulière) pour (0;0;1;2;3;…) et ensuite sortir les 0 pour conclure que (1;2;3;…) est bien SSSLR (adjectif ‘super-sommable de façon stable linéaire et régulière’) et ensuite la contradiction. Mais du coup ça prouverait que (0;0;1;2;3) n’est pas SSSLR et non pas (1;2;3;…) (non, ne me regardez pas avec ces yeux, ce ne sont vraiment pas les mêmes suites!). D’autant plus que quand d’autres en parlent, ils utilisent la caractérisation par l’invariabilité de la sommation par insertion d’un zéro (qui est, si on prend la bonne définition) équivalente à celle de ce blog.
Autre chose: La sommation devrait semble-t-il fonctionner avec l’espace sur lequel elle opère. Et la stabilité de l’espace doit faire partie de la définition de la stabilité de la sommation. Autrement, dit la SSSLR semble mieux se définir comme ou couple (S,H) ou H est un sous-espace vectoriel de celui des suites tel qu’une suite y appartient si et seulement si la suite tronquée du premier terme y est aussi ou de manière équivalente H est un sev tel qu’une suite y appartient si et seulement si la même suite avec un zéro devant y est aussi.
Serait-ce simplement pour chipoter? En fait, ça éclaire un point fort intéressant que je me suis demandé en lisant les calculs heuristiques.
Si le calcul de A permet celui de B puis celui de S, on devrait donc avoir que S est SSSLR (oui j’utilise aussi l’adjectif pour la somme…). Soyons plus rigoureux, S’ est SSSLR (ou S’ est la suite des entiers avec un zéro intercalé une fois sur deux). Cette disparition de zéro (non autorisé) et qui était le premier suspect, n’a en fait (en soi) rien à se rapprocher (si ce n’est qu’on rajoute une propriété supplémentaire à notre sommation). Bah oui, car on sait que A et B sont bien SSSLR (il existe des sommations leur assignant un valeur, et c’est toujours la même). Mais le soucis c’est que la preuve de Matheux marche aussi avec S’. Il n’est pas dur de se convaincre qu’en insérant un nombre infini de zéros de manière régulière à la suite des entiers (dans notre cas, une fois sur deux), la même manipulation conduit à 1 = 0 (avec la stabilité comme étant la possibilité d’insertion et de retrait de 0). Du coup S’ ne peut pas non plus être SSSLR. Mézalor pourquoi a-t-on bien A et B sommables et pas S’? Ne devrait-on pas avoir A sommable, donc B sommable, donc S’ sommable? N’est ce pas ce que ‘prouve’ le calcul heuristique? Faux! le calcul ‘prouve’ en fait ceci: « Si A est SSSLR alors A vaut 1/2. Si B est SSSLR et A est SSSLR alors B vaut 1/4 (autrement dit, on ne déduit pas de la supposition de l’existence d’une SSSLR pour A celle de B, on la suppose). Et enfin si S et SSSLR (et A et B aussi) alors S’ l’est et S – 1/4 = 4S’. »
Ainsi donc, L’existence d’une SSSLR pour A n’implique pas que celle-ci somme B (prendre Césaro pour exemple). Alors comment sait-on que B est SSSLR? A cause d’Abel comme le précise l’article. Abel est bien une SSSLR et peut sommer B. (Dit en passant une Méthode qui somme B, somme aussi nécessairement A….sauriez-vous le prouver?)
Et enfin le calcul heuristique sur S prouve qu’une méthode marchant pour B, marche pour S si et seulement si elle marche pour S’. car en partant de l’une on obtient l’autre en utilisant B.
Enfin, pour ceux que ça intéresse je précise qu’un sous-espace quasi-immédiat auquel on peut étendre la notion de somme est celui des suites à sommes partielles bornées. En utilisant une Limite de Banach (définie sur L infini) sur la suite des sommes partielles, on définit ainsi une SSSLR sur l’espace des suites à somme partielle bornée. Par l’étude des limites de Banach, on a même un critère d’unicité de la valeur affectée possible (évidemment pour les suites à somme partielle bornée). Donc on sait la propriété que doit vérifier la suite des sommes partielles d’une suite pour que cette dernière soit SSSLR de manière unique.
J’ai lu plusieurs fois les commentaires des deux blogs, mais ma mémoire n’est pas parfaite donc dsl s’il y a des redites.
Petit détail pour chipoter. Techniquement la vignette du début de l’article est fausse. Dedans, la somme part de 0 alors que la somme dont il est question dans l’article part de 1 (on somme 1+2+3+…. et non 0+1+2+3…).
Sachant en plus qu’on a 1+2+3+……= -1/12 et 0+1+2+3+…= 5/12. 😉
Bonsoir Manu,
la longueur de vos 2 réponses et le flot de détails que vous donnez avec ferveur et enthousiasme, me laissent penser que je vous ai pour le moins légèrement irrité ;-). Je suis obligé de reconnaitre que l’approche mathématique que vous décrivez et celle que je présente ne sont pas compatibles. Je n’ai aucunement cherché à être offensant mais simplement logique comme le demande une démonstration mathématique mais je constate que malheureusement les logiques que nous décrivons sont incompatibles. Je peux le comprendre au même titre que 1+1 = 0 en logique binaire et c’est ce que semble proposer la SSSLR étrange que je ne connais pas. Par contre en math classique 1+2+3+…+n =n.(n+1)/2 démontré par Gauss selon la légende en 1786 et selon la SSSLR 1+2+3+…n=-1/12. Qui a raison ? Les deux ? Si oui au risque d’être provocateur, peut-on écrire que n.(n+1)/2 = -1/12 et donc que n = 0,21 ou n=0,79 ? Je constate qu’avec la meilleurs volonté de rassembler, on n’y arrivera pas.
Bien cordialement et sans rancune.
Alain
Pas d’irritation envers vous personnellement Alain,mais envers votre incompréhension (probablement due à un manque d’approfondissement de la question – j’entends par là ‘lire l’article en entier’). Il n’y a absolument pas ‘deux logiques’, mais bien une seule. Juste un ou deux détails que vous ne percevez pas (malheureusement, par désinformation). Je m’explique.
L’égalité démontrée par Gauss dont vous parlez ne concerne pas du tout cet article! Et c’est là que votre erreur réside (et celle de tout autre qui raillent cette « mascarade »). Comme l’indiquent les sous-titres cités, dans cette « somme » il n’y a pas de notion de « somme qui s’arrête à n » ou « tend ». On essaie simplement de comprendre s’il peut exister un « autre chose » qui généralise l’addition dont vous parlez (l’addition d’un nombre de terme fini).
Basiquement les contradictions de ce type (j’inclue tous les commentaires ressemblant au votre) sont du type « mais regarde un nombre au carré peut pas être négatif, parce que si tu prends x réel alors x² est positif ». A cette phrase tout bon élève de terminale (ou 1ère année de sup je vous l’accorde) se tape la tête contre le mur, et précise alors qu’on cherche à généraliser la notion de nombre, et que dans ce nouvel ensemble un carré peut effectivement être négatif.
Une version plus basique? L’élève de CE1 qui se borne à préciser qu’on ne peut soustraire 5 à 2 parce que ça ne donne pas un entier (il entend par là entier naturel). Si! Dans une généralisation de la notion de nombre, c’est possible.
Donc la question qui se pose est simplement, est-ce que les axiomes admis qui constituent nos mathématiques impliquent aussi l’existence de telles structures (qui permettent ces généralisations)? Pour les nombres complexes oui. Pour les entiers relatifs aussi. En acceptant ce qui est admis mathématiquement et sur lequel se base nos notions de nombres entiers naturels et respectivement réels, on est forcé de constater qu’il existe des objets plus généraux (on choisit de toujours les appeler « nombres » pour les complexes ou « entiers » pour les entiers relatifs) aux propriétés un peu plus « étranges ». Nos à priori sont à jeter à la poubelles à la lumière de la raison. Une démonstration en bonne et due forme, bien solide et étayée suffit à convaincre tout élève attentif (d’un niveau poussé je l’admets) que les nombres complexes/les entiers relatifs existent (en tant que choses abstraites) dans l’univers mathématique.
La somme dont il est question n’est PAS une somme finie. ça n’a donc aucun sens de l’arrêter à n. L’écriture de David ne le laisse peut être pas suggérer clairement et est malheureuse (il faut avouer que le 1+2+3+….= -1/12 est sensas et en jette!). Pour sa défense, il s’agit de calculs heuristiques. Des sortes d’à peu près pas super rigoureux qui, dans le bon cadre, trouvent un sens rigoureux. Mais là on fait de l’écriture en mode à peu près, parce que c’est comme ça qu’on trouve et comprend le fonctionnement des choses pour ensuite les démontrer rigoureusement. Et c’est ce qu’a fait Euler. c’était faux oui. Mais pas si faux que ça. C’est le but de la suite de montrer que non Euler a mis le doigt sur un phénomène intéressant.Donc ce n’est pas une somme finie je disais.
D’ailleurs, on ne sait pas, à priori, faire une somme finie comme l’explique l’article. On le peut grâce à une propriété bien utile de la somme de deux éléments. Ensuite, on essaie de voir s’il existe bien un ‘quelque chose’ qui généralise la somme finie, de la même manière que la somme finie généralise la somme de 2 réels. Et il se trouve que oui! Avec les propriétés sus-mentionnées. On peut le définir dans le cadre de ce qu’on appelle l’études des séries (limites de sommes partielles) qui généralise la notion de somme finie, et correspond « plutôt bien » à la notion de « somme infinie ». Mais comme toutes généralisations, des choses ne sont plus vraies (cf article). Mais on voudrait savoir si on peut faire encore PLUS que ça. Du coup, on regarde s’il existe une notion qui généralise cette association de « somme » à un nombre infini de termes. Et avec certaines propriétés, oui. Mais cette généralisation se fait par un processus abstrait (ou algébrique :P); ça n’a à priori rien à voir avec une quelconque notion de tendre ou de limite (même si certaines de ces opérations sont construites de cette façon dans la pratique). Et on peut montrer que oui ça existe et en fournir des exemples (qui sont d’ailleurs donnés dans l’article).
Conclusion? Il existe bien un truc, qui correspond à peu près à notre notion intuitive de somme et qui marche pour un nombre infini de termes. Mais comme toutes généralisations, on perd des propriétés quand les concepts englobent plus de choses. Dire que « c’est bizarre qu’une « somme » infinie de terme positif donne quelque chose de négatif » est du même niveau intellectuel qu’objecter « qu’un carré ne peut que être positif » ou « qu’une différence d’entiers n’a de sens que quand le premier est plus grand que le deuxième ». Au mieux de l’ignorance (on pardonne les primaires, collégiens et les lycéens de 2nde et 1ère). Au pire de la bêtise pure et dure.
Les propriétés d’avants ne marchent plus; parce que justement on a généralisé! Les seules propriétés qui se sont gardées et que l’on peut réutiliser sont globalement celles qui sont citées dans l’article.
Donc votre calcul ne montre rien. Vous parlez de tomates et de carottes. La somme des tomates vaut n(n+1)/2. La somme des carottes vaut -1/12 (dans un sens encore à préciser/trouver, je l’accorde). Encore une fois, la somme de (1;2;3;…) concerne TOUS les termes de la somme « d’un coup ». C’est complètement incomparable à n’importe quelle somme finie finie du type 1+2+3+….+n (qui s’arrête ici à l’entier n) et ce quel que soit l’entier que prenez. La somme finie ne donne aucune espèce d’intuition (et ce quel que soit la grandeur du nombre que vous prendrez), tout simplement parce que le fait de sommer un nombre fini de choses et un nombre infini (autre que par les séries) sont COMPLÈTEMENT différents. Aussi différents que la « grandeur » de n’importe quel entier avec celle de l’infini. ça n’a juste rien à voir. Des tomates et des carottes; des bonbons et des chips; du carton et de la féraille…bref rien!
Le seul point commun et propriétés qui font sens, sont celles décrites dans l’article.
Pour votre question, vous ne pouviez pas le savoir. Mais si vous n’avez pas lu l’article, et à fortiori les commentaires donc, vous êtes passé à côté du fait qu’on a précisé (et démontré) que la somme 1+1+1+….(et non ça ne s’arrête pas) n’est pas « sommable » selon cette méthode ou n’est pas SSSLR. Maintenant, il semblerait qu’une sommation encore plus générale que celle décrite ici sommerait celle-ci (et celle des entiers aussi d’ailleurs). On en est pas sûr, parce cette « sommation » n’a pas été identifiée et on ne sait pas vraiment si elle existe (l’article en parle), mais plusieurs approches semblent indiquer que oui. La plus rigoureuse étant la régularisation zêta. Sur ce dernier point (l’approche qui convainc le plus), personne n’est vraiment d’accord.
Je ne peux pas vous le prouver, mais il semble que A0 = -1/2. Je peux néanmoins définir une « sommation » pour laquelle ce résultat est vrai (et démontré). Après quant à savoir pourquoi cette sommation donne cette valeur, quelles sont exactement ses propriétés et y en a-t-il d’autres qui donnent d’autres valeurs ou pourquoi choisir cette sommation là comme définition de la somme généralisée plutôt qu’une autre donnant d’autres valeurs à A0 (si c’est le cas)….ce sont des questions encore ouvertes.
Pour A1, A2, A3, Ax, je donne ma langue au chat. Notre niveau de connaissance est encore trop timide pour attaquer ce genre de questions (notamment à cause du fait qu’une sommation encore plus générale que la SSSLR perdrait, semble-t-il, la propriété de stabilité – ce qui rend les calculs assez compliqués). mais on peut prouver que ces sommes ne peuvent être sommées de manière SSSLR.
Pour votre dernière phrase, non car vous utilisez sans vous en rendre compte des propriétés qui n’ont pas été introduites. Vous sommez une infinités de sommes. Pour faire cela, il faudrait donner un sens à une somme infinie de SUITES (un sens plus général que la notion de série de suites). Et pour faire cela, il faudrait déjà qu’on comprenne la notion la plus générale possible de somme infinie de NOMBRES (ce qui est justement le soucis ici!). Autrement dit, ce que vous dîtes ne s’écrit pas, et n’a pour le moment aucun sens, parce que justement la quasi-totalité des questions concernant cet article sont encore laissées ouvertes.
En espérant être assez clair et explicite des mes explications.
Intéressant point de vue. Détrompez-vous, mes questions ne sont pas anodines et sont réfléchies. Elles sont là pour tester la logique et les limites de la SSSLR que d’ailleurs vous confirmez comme incomplète à ce jour avec quelques lacunes: je n’ai pas eu besoin de l’écrire, c’est vous qui le dites.
Comment une théorie non étayée par des résultats expérimentaux démontrables peut-elle être convaincante? Elle ne sera valable et acceptée que lorsque ces lacunes auront été traitées de manière précise sans se réfugier dans des « questions ouvertes » qui pourraient laisser supposer que tout ce qui est fait jusqu’à présent est juste. Une bonne théorie doit être remise en cause par tous avant de pouvoir convaincre un plus grand nombre. Sinon on est dans le domaine de la religion et de la croyance.
Je ne comprends pas comment vous calculez A0 = (0+1+1+1+1+…)
On peut écrire A0= 0+ (1+1+1+1+…) propriété de stabilité
et donc A0 = 0 + A = A = 1/2 et non -1/2 ? Pourquoi trouvez-vous -1/2 ?
Bon je ne résiste pas à citer quelques pensées de Pierre DAC dont je dirai que certaine(s) s’applique(nt) aussi à moi pour ne vexer personne:
“Si tous ceux qui croient avoir raison n’avaient pas tort, la vérité ne serait pas loin.”
« C’est quand on a raison qu’il est difficile de prouver qu’on n’a pas tort.”
“Avec le mot « si » on peut faire tout ce qu’on ne peut pas faire.”
“Avec de la méthode et de la logique on peut arriver à tout aussi bien qu’à rien.”
“Rien ne sert de prouver si on n’est pas foutu de démontrer.”
“Si les points de suspension pouvaient parler, ils pourraient en dire des choses et des choses !”
“Rien de ce qui est fini n’est jamais complètement achevé tant que tout ce qui est commencé n’est pas totalement terminé.”
“Si la préhistoire a précédé l’histoire, il n’a jamais été démontré que la prescience ait précédé la science.”
J’espère que ces échanges seront pris positivement.
😮 Je m’avoue vaincu. Je suis impressionné, et il en faut pour. Je passe complètement sur les citations, qui en disent très long sur la pertinence de votre réponse.
Pour répondre à vos questions un peu plus légitimes, A0 se calcule grâce à la régularisation zêta (ce que vous avez écrit correspond à A1; ce n’est pas la même chose du tout). C’est assez technique donc hors de question de rentrer dans les détails. Mais regardez la page wiki, le paragraphe qui en parle et vous allez aisément comprendre l’idée (je l’espère).
Et non A0 ne se calcule pas avec une SSSRL!!! Puisque qu’on a démontré (comme je vous l’ai précisé) qu’elle n’est PAS SS-Stable-RL. Donc NON, on ne peut pas utiliser une propriété de stabilité pour son calcul.
D’autant plus que vous mélangez votre propre A0 et le A de l’article…
Tester la logique et les limites de la SSSLR? C’est peut être une blague. Le fait que je l’ai confirmée « incomplète » avec « des lacunes » aussi (surement).
Donc le fait de ne pas savoir faire certains calculs ou répondre à des questions rend la théorie bancale?
On peut donc jeter à la poubelle l’arithmétique parce qu’on ne sait pas combien de nombres premiers jumeaux il y a?
Ou jeter les nombres complexes à la poubelle parce qu’on ne sait si les zéros non triviaux de zeta ont tous une partie réelle valant 1/2?
Donc une théorie mathématique n’est valable que quand on sait répondre à toutes les questions qu’elle pose?
Vous vous rendez compte de ce que vous dîtes j’espère?
La sommation des séries divergentes est étayée. Et ce qui est fait ici EST juste. Tout comme l’existence des complexes est étayée. Des méthodes SSSLR existent et ça se démontre (j’en ai fourni un exemple plus haut). C’est un truc qu’on trouve dans des bouquins de maths et qu’on enseigne, et on peut en vérifier le raisonnement du début. Le livre de Hardy est cité, ainsi qu’un excellent (mais très pointu) article de Terrence Tao. Vous pouvez vérifier si vous le voulez.
Lisez. Vos réflexions sont très (mais alors très) loin d’être réfléchies, tout simplement parce que vous ne savez ni ne comprenez ce que vous dîtes. Et j’avoue ne pas percevoir un effort particulier…Franchement, lisez. Je ne crois pas que vous prenez la peine ne serait-ce que de lire (sérieusement) ce que je vous dis (alors encore moins l’article; alors encore moins d’autres document qui en parlent). Et pourtant, c’est pas si dur….il s’agit juste d’un coup de google ou de wikipédia. Et pour les grincheux, un bon google scholar pour voir les articles de recherche qui en parlent. Mais sérieusement, lisez. En gros, à part à quelques exceptions près, je vous ai juste résumé ce que dis et explique l’article. Attention: on n’est même pas dans les implications et la déduction à partir de ce que dit l’article mais dans les questions de base qu’il aborde noir sur blanc.
Quand on ne sait même pas (ni ne comprend) ce que dis la dite théorie, on n’est pas en droit de la remettre en cause, là c’est de la croyance. Surtout après insistance à tergiverser sur des points aussi évidents qui ont été réglé depuis (très) longtemps.
Mettre à l’épreuve la théorie? Comme je vous l’ai dit vos questions ne remettent rien du tout en question puisque la plupart n’ont même pas lieu d’être. Et regarder ces « lacunes » est assurément tout sauf scientifique. Des résultats sont bel et biens démontrés (sisi avec de vraies preuves), mais comme tout pan des maths certains calculs ou certains points sont encore inexplorés.
Question pour David.
Comment traitez-vous en SSSLR les sommes suivantes:
A0= 1+1+1+1+1+…; A1=0+1+1+1+1+…; A2= 0+0+1+1+1+1+…; A3=0+0+0+1+1+1+1+…; Ax=0+0+0…+1+1+1+…; …
puis S = 1+2+3+4+5+….
Peut-on écrire que S = A0+A1+A2+A3+…. et est-ce que sa valeur est toujours -1/12? Quelles sont les valeurs de A0,, A1, A2, A3, …
Merci
Alain
Encore une fois rien de personnel Alain 😉
Mon message s’adresse à TOUTES les réponses disant à peu près les mêmes choses que vous.
Cordialement,
Manu