Propagation d’épidémies et graphes aléatoires

Comprendre comment se propagent les épidémies peut être d’une importance capitale. Qu’il s’agisse de maladies ou de virus informatiques, il est utile d’analyser à partir de quel point une épidémie peut s’emballer, ou bien quelle est la meilleure manière de traiter une population si on possède un antidote.

Pour étudier cela avec des simulations, on fait appel à des modèles où les individus sont représentés par des noeuds d’un réseau dont les liens sont aléatoires et figurent la possible propagation de l’épidémie : on parle de graphes aléatoires.

Un modèle simple d’épidémie

Imaginons qu’à l’endroit où vous travaillez, une épidémie soit susceptible de se propager. Heureusement au cours d’une journée, tout le monde ne rencontre pas tout le monde. De surcroit, si deux personnes se croisent, il n’est pas dit que le virus passe, car ce dernier ne va se transmettre que si le contact est suffisamment proche.

Supposons pour fixer les idées qu’il y ait 30 personnes, nous allons représenter ces personnes par des points sur un graphique, que l’on va disposer en cercle (leur position précise n’a pas d’importance).

Imaginons qu’au cours d’une journée on croise en moyenne 40% des autres personnes, et que seulement 10% de ces contacts soient « proches ». Au global entre 2 personnes prises au hasard, il n’y a donc que 4% de probabilité d’une transmission du virus.

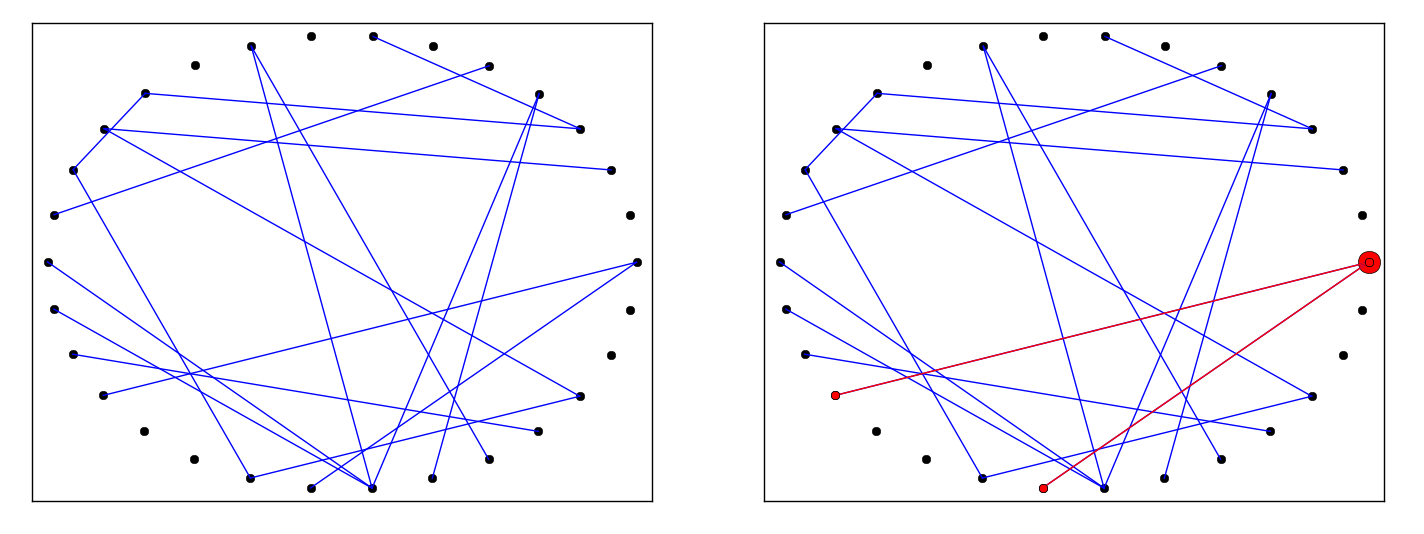
Pour représenter cela, on va considérer tous les liens possibles dans le réseau, et en tirer au hasard 4% qui seront actifs et donc susceptibles de transmettre le virus. On obtient un graphique comme celui représenté ci-dessous à gauche.

Introduisons maintenant un individu malade, représenté ici par un gros cercle rouge. Il n’y a plus qu’à propager le virus le long des liens actifs pour connaître la taille totale de la population infectée : ici seulement 3 personnes. Il ne s’agit que d’un cas particulier, mais si on dispose d’un ordinateur, on peut simuler une telle situation un grand nombre de fois, en tirant à chaque fois au hasard 4% des liens qui seront actifs et en comptant la taille de la population infectée. Avec 30 individus et 4% de propagation, on va s’apercevoir que dans la quasi-totalité des cas, la taille de la population infectée est petite, quelques individus tout au plus.

La notion de seuil épidémique

Répétons maintenant l’expérience en changeant un tout petit peu les chiffres. On va simplement doubler la probabilité que le virus se transmette. On reprend donc nos 30 individus et on tire à nouveau au hasard les liens actifs, mais il y en aura cette fois 8% au lieu de 4%.

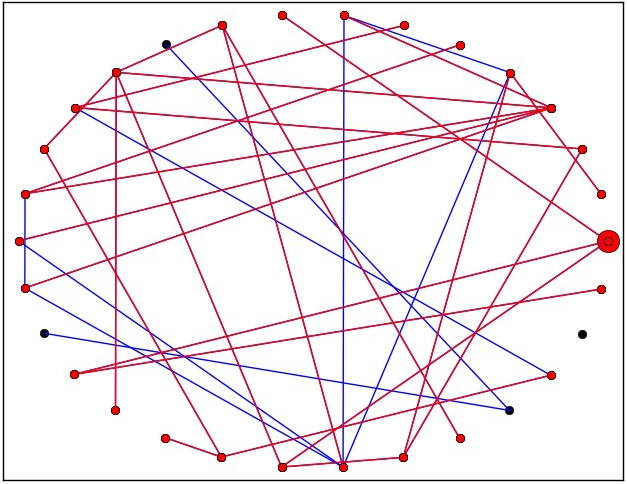
On obtient un graphique comme celui-ci contre : comme vous pouvez le constater, si on introduit un individu malade, la maladie se transmet cette fois à tout le monde ou presque ! En passant simplement de 4% à 8% de probabilité, on a franchit un seuil qui conduit à une propagation quasi-totale. On parle de seuil épidémique.

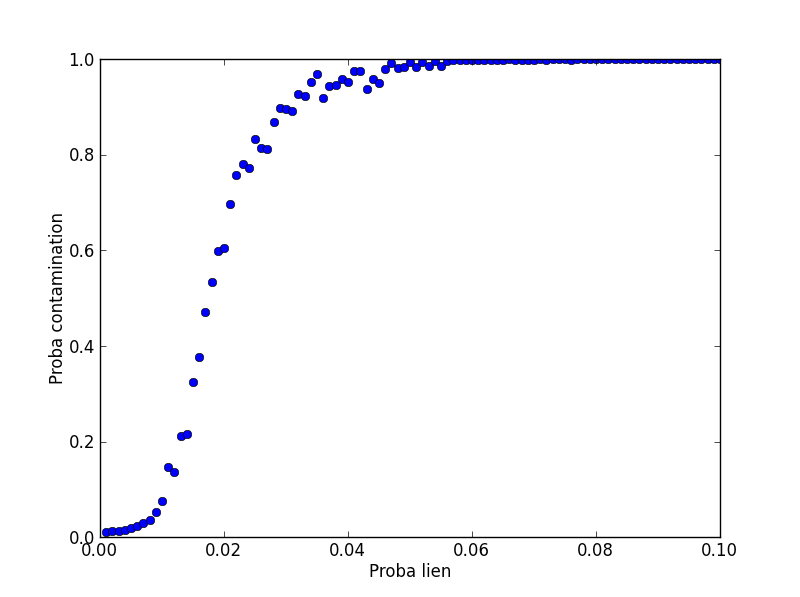
Pour illustrer cet effet de seuil, j’ai fait une simulation plus riche : en prenant 100 individus, j’ai fait varier la probabilité de propagation de 0.1% à 10%, et j’ai répété 100 fois l’expérience pour chaque niveau. En calculant la taille moyenne de l’ensemble infecté, on obtient donc la probabilité de contamination en fonction de la probabilité de propagation. Le résultat est représenté ci-dessous.

On voit que pour des probabilités de propagation faibles, la probabilité de contamination est très faible, alors que pour des probabilités de propagation élevées, elle est de 1 : c’est-à-dire que tout le monde tombe malade ! Entre les deux, on voit très nettement se dessiner le seuil épidémique à partir d’environ 1%, et la transition violente qui l’accompagne. Notez que la position du seuil dépend du nombre d’individus : dans cette simulation j’ai utilisé 100 personnes (au lieu de 30 sur les dessins précédents), et donc le seuil critique a changé : à 4% on est déjà en contamination quasi-totale !

Le modèle d’Erdös-Rényi

Le modèle que j’ai présenté ci-dessous, et la transition violente qui le caractérise, a été introduit à la fin des années 50 par les mathématiciens hongrois Erdös et Rényi. Ils ont démontré que la transition violente se produit quand la probabilité de transmission p est égale à 1/N, où N est le nombre de noeuds du réseau. Cela signifie que le seuil épidémique est franchi dès qu’il existe en moyenne au moins un lien par personne. Tout cela est finalement assez logique !

Le modèle d’Erdös-Rényi est intéressant pour commencer, mais il n’est en fait pas très réaliste. Dans ce modèle, le nombre moyen de liens que possède un noeud est égal à p.N, et la plupart des noeuds ont un nombre de connexions proche de cette valeur moyenne. On dit que ce modèle est homogène, car tous les individus jouent plus ou moins un rôle analogue.

Mais dans un véritable réseau (qu’il soit informatique ou social), on constate que beaucoup d’individus possèdent peu de connexions alors que certains autres en possèdent un très grand nombre. Les réseaux réels sont hétérogènes et il faut donc se tourner vers une autre représentation.

Réseaux réels et petits mondes

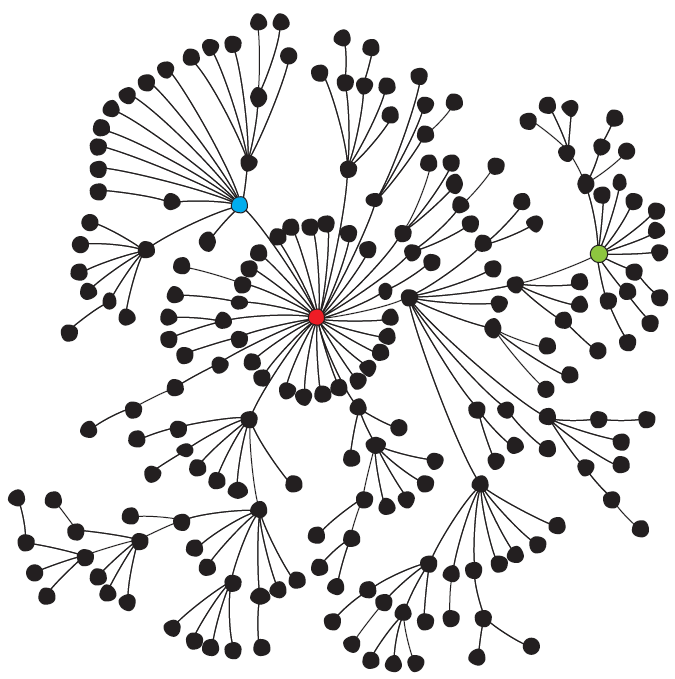De nombreux réseaux ont été analysés à partir de données réelles : l’architecture d’Internet, les collaborations d’acteurs dans le monde du cinéma et même les réseaux de partenaires sexuels [1] ! On constate qu’aucun de ces réseaux n’est correctement représenté par un modèle de Erdös-Rényi, car certains individus ont un nombre de liens avec les autres bien plus grand que la moyenne. Un réseau réel ressemble donc plutôt à ce qui est représenté ci-contre. On voit qu’un tel réseau est hétérogène et que certains noeuds ont un statut particulier.

Grâce aux individus très connectés qui jouent le rôle de « hub », les réseaux réels possèdent une propriété que l’on appelle « petit monde« . Cela signifie que l’on peut aller de n’importe quel point du réseau à un autre par un chemin assez court. Cela correspond à cette idée populaire qui dit que l’on peut trouver un lien entre 2 personnes prises au hasard dans un pays en moins de 6 connexions.

Évidemment, la propagation dans des réseaux de ce type se fait bien plus facilement que dans un réseau de type Erdös-Rényi ! La contrepartie, c’est que leur structure particulière permet d’imaginer des stratégies de traitement plus efficaces qu’avec un réseau homogène. Si on immunise quelques noeuds bien choisis, on peut grandement ralentir la propagation.

Il existe donc tout un champ de recherche consacré à la mise au point de stratégies de traitement. Pour cela, on voudrait évidemment traiter en priorité les « hubs », mais on ne sait pas forcément à l’avance qui ils sont. Un exemple très simple de stratégie possible, c’est de tirer au hasard quelques individus, et d’immuniser tous ceux qui leur sont liés. On a ainsi une manière de toucher naturellement les individus les plus connectés !

Pour aller plus loin : les réseaux « scale-free »

Les propriétés des réseaux réels ont été très abondamment étudiées ces 20 dernières années. Mathématiquement parlant, la propriété principale qui les caractérise est la loi de distribution du nombre de connexion d’un noeud pris au hasard. Dans un réseau homogène de type Erdös-Rényi, il s’agit d’une distribution de Poisson, que l’on peut en gros rapprocher d’une gaussienne. C’est-à-dire que si les individus ont en moyenne 10 liens, on trouvera pas mal de personnes avec entre 3 et 20 liens, mais très peu au-delà. Dans un réseau réel, on trouve des individus avec un très grand nombre de liens, ce qui fait que la loi de distribution ne peut pas être une gaussienne. 

Dans beaucoup de réseaux réels, cette distribution est celle d’une loi de puissance, c’est-à-dire que la probabilité P(k) qu’un individu possède k liens est donnée par une loi du genre

\(P(k) \sim \frac{1}{k^\gamma}\)

où l’exposant \(\gamma\) vaut en général entre 2 et 3. Comme je l’expliquais dans mon billet sur les fluctuations de la Bourse, ces lois de puissance possèdent beaucoup plus d’évènements extrêmes que les braves courbes en cloche : on aura donc un nombre significatif d’individus avec beaucoup plus de liens que les autres.

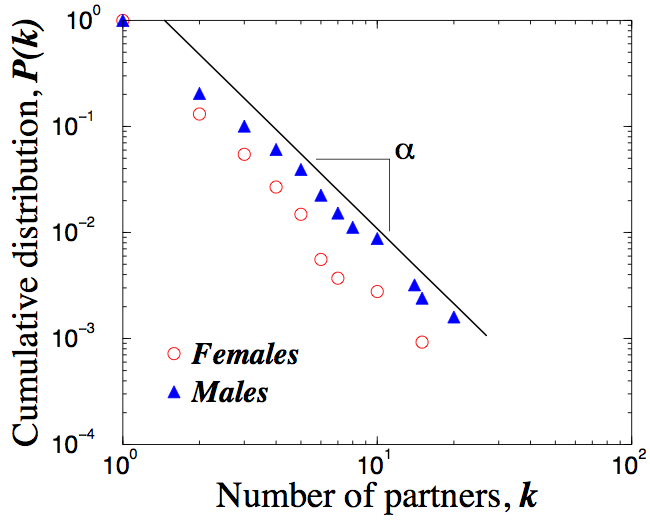Un exemple ? Les relations sexuelles en Suède [1]. Les auteurs de ce papier ont demandé à 4800 Suédois et Suédoises le nombre de partenaires sexuels qu’ils avaient eu l’année passée. Ils ont ensuite analysé la probabilité P(k) d’avoir eu k partenaires. Comme illustré ci-contre, la représentation de P(k) en échelle log-log fait apparaître une belle droite de coefficient \(\alpha\) égal à environ 2.4. C’est le signe d’une distribution en loi de puissance ! Si la loi avait été gaussienne, on n’aurait eu quasiment personne revendiquant plus de 10 partenaires dans l’année. Ah oui, on constate aussi ce phénomène bien connus : les hommes s’attribuent plus de conquêtes que les femmes !

Revenons à nos réseaux possédant une distribution de nombre de connexions en loi de puissance. Des analyses identiques ont donc été faites pour les réseaux informatiques ou encore les réseaux de collaboration des acteurs à Hollywood. On retrouve toujours le même phénomène avec une loi de puissance (et un exposant entre 2 et 3), dont découle notamment un effet petit monde : les individus les plus connectés permettent facilement de relier entre elles 2 personnes prises au hasard en un petit nombre de lien. A Hollywood, il semble que l’individu le plus connecté soit Kevin Bacon.

Ces réseaux sont appelés « scale free » (sans échelle) car la loi de puissance ne fait intervenir aucune taille caractéristique (contrairement à la gaussienne où la valeur moyenne impose une échelle caractéristique). Pour représenter ces réseaux « scale-free », les chercheurs se sont beaucoup gratté la tête : il fallait trouver un modèle de réseau aléatoire assez différent de celui d’Erdös-Rényi. Deux solutions ont finalement été proposées.

L’une permet de construire explicitement des réseaux de type « petit monde » [2]. On part d’un réseau où chaque individu n’est connecté qu’à ses plus proches voisins, et on ajoute aléatoirement des connexions qui connectent des individus très éloignés. Mais pour autant que je le comprenne, ceci ne donne pas la propriété de « scale free ».

La solution a été trouvée finalement par un modèle d’une élégance et d’une simplicité fantastique : il suffit de construire le réseau de manière explicite à la manière dont se construisent les vrais réseaux, c’est-à-dire progressivement. L’idée clé est la suivante : la probabilité qu’un nouvel individu se connecte à un individu déjà présent est proportionnelle au nombre de connexions ce dernier que possède déjà, ou autrement dit « the rich get richer ». Pour illustrer cette idée, vous pouvez penser au réseau informatique (on va tous chercher à se connecter à un hub très connecté) et même au réseau des relations sexuelles : ceux ayant déjà eu beaucoup de partenaires possèdent certainement le talent et le désir de se connecter encore plus.

Bref, dans un de ces papiers simples et lumineux que j’aurai aimé écrire [3], les deux auteurs de ce modèle l’ont simulé avec divers paramètres, et ont montré que cela donnait toujours des réseaux avec une distribution des liens en loi de puissance avec un exposant -3. Bingo !

Un point que je voulais préciser : dans mes simulations épidémiques, j’ai complètement ignoré la question de la dynamique. J’ai supposé en gros que la transmission était instantanée et qu’il n’y avait pas de guérison ou de mort. Dans les vrais modèles, on prend ça en compte et on simule la propagation dynamique. On parle alors de seuil épidémique quand le taux de propagation de la maladie (rapporté à son taux de guérison) dépasse une certaine valeur critique. La question de la propagation dans les réseaux « scale-free » a d’ailleurs été résolue récemment, et il a été montré que pour ces derniers, le seuil épidémique est nul [4] ! Aussi petit que soit le taux d’infection, cela finira toujours par dégénérer en épidémie.

D’ailleurs pour faire le lien avec le réseau des partenaires sexuels, on estime que la propagation du virus du SIDA à l’échelle mondiale a été facilitée par quelques « hubs » possédant un grand nombre de partenaires. On cite souvent le cas de Gaëtan Dugas, un stewart de Air Canada qui au début des années 80 aurait eu plus de 2500 relations en quelques années. Mentionnons tout de même que les spécialistes récusent la théorie du « patient zéro » selon laquelle un unique individu aurait été à l’origine responsable de toute la transmission.

Références :

Comme vous pourrez le constater si vous lisez ces papiers, ce domaine de recherche a été un temps très à la mode, et il contient un grand nombre des ingrédients magiques dont parlait Xochipilli ici : transitions de phase, lois de puissance et autres phénomènes critiques.

[1] Fredrik Liljeros et al., « The Web of Human Sexual Contacts », Nature 411, 907-908 (2001) arXiv:cond-mat/0106507 (j’aime l’idée qu’un papier sur le sexe soit publié dans « cond-mat », l’arXiv de matière condensée)

[2] Watts, Duncan J.; Strogatz, Steven H. « Collective dynamics of ‘small-world’ networks ». Nature 393 (1998): 440–442

[3] Barabási, Albert-László; Albert, Réka « Emergence of scaling in random networks ». Science 286 (1999): 509–512. arXiv:cond-mat/9910332

[4] Romualdo Pastor-Satorras and Alessandro Vespignani, Epidemic Spreading in Scale-Free Networks, Phys. Rev. Lett. 86, 3200–3203 (2001) arXiv:cond-mat/0010317