 En mathématiques, il existe quelques problèmes très simples à énoncer mais incroyablement difficiles à résoudre. C’est particulièrement vrai en arithmétique, et j’ai déjà eu l’occasion d’écrire des billets sur la conjecture de Goldbach (ici) et sur celle de Syracuse (là).
En mathématiques, il existe quelques problèmes très simples à énoncer mais incroyablement difficiles à résoudre. C’est particulièrement vrai en arithmétique, et j’ai déjà eu l’occasion d’écrire des billets sur la conjecture de Goldbach (ici) et sur celle de Syracuse (là).
Aujourd’hui, nous allons voir qu’en géométrie aussi, il existe des conjectures qu’un collégien peut comprendre mais sur lesquelles les meilleurs mathématiciens du monde se cassent les dents. Et comme la géométrie est partout autour de nous, cela va nous permettre de faire un tour dans le monde des abeilles et celui des bulles de savon.
Un problème de pavage
C’est décidé, vous allez refaire le carrelage de votre cuisine ! Vous vous rendez donc dans votre magasin de bricolage préféré pour examiner les différents modèles disponibles. Il y a de tout : carrés, rectangles, hexagones, triangles, mais aussi des formes plus compliquées comme des pavages à la Escher. Le vendeur vous précise que quel que soit le modèle, le carreau fait toujours la même surface. Comment choisir ?
Pour ma part, je suis assez nul pour faire les joints. Si vous êtes comme moi, vous allez choisir le carreau qui donne le moins de joints à faire, et c’est celui dont le périmètre est le plus petit. Mais quelle est donc la forme géométrique qui pour une surface donnée possède le périmètre le plus petit ? La réponse est connue depuis longtemps : il s’agit du disque. Mais vous voyez bien qu’avec des disques on ne peut pas faire un carrelage ! Il nous faut donc trouver la forme géométrique qui possède le plus petit périmètre, et qui permet de paver une surface.
Là aussi la réponse est connue depuis l’antiquité : il s’agit de l’hexagone régulier. Enfin, je dis « la réponse est connue », mais en deux millénaires, personne n’avait réussi à le démontrer vraiment ! Et il a fallut attendre 1999 pour que le mathématicien Thomas Hales fournisse une preuve rigoureuse de ce résultat. Un bel exemple d’une conjecture très simple qui a résisté à des générations de mathématiciens.
Bref, c’est donc le carrelage avec des hexagones qui vous permet de limiter au maximum la quantité de joints.
 Les hexagones dans la nature
Les hexagones dans la nature
La nature fait souvent bien les choses, et c’est donc sans surprise que le pavage par des hexagones se retrouve chez nos amis les bêtes, et notamment par l’exemple bien connu des alvéoles des nids d’abeilles.
De même que cette forme permet de minimiser les joints de carrelage, elle permet de limiter la quantité de cire a utiliser pour créer les alvéoles. Le fait que le pavage hexagonal soit le meilleur est d’ailleurs maintenant connu comme le théorème du nid d’abeille.
Est-ce à dire que les abeilles ont réussi à résoudre un problème de géométrie très compliqué ? Pour Darwin, il s’agit plutôt d’un effet de sélection naturelle : les abeilles réalisant les structures les plus économes sont celles qui ont été sélectionnées par l’évolution.
Mais comme nous l’explique Xochipilli sur son blog le Webinet des curiosités, l’explication est peut être encore plus simple. On sait que si on ne cherche pas à créer un pavage, alors la forme de plus petit périmètre est le disque. Et si on juxtapose des disques et qu’on les déforme pour les forcer à se toucher, on obtient assez naturellement un pavage hexagonal ! Alors, les abeilles, pas si géniales que ça ?
Et en 3 dimensions ? Le problème de Kelvin
Maintenant que l’on connait la forme de plus petit périmètre qui permet de remplir une surface, on peut passer à la question supérieure : quelle est le pavage de l’espace qui possède la plus petite surface ? Pensez-vous que ce soit le cube ? Non, ce serait trop simple !
 Le physicien britannique Lord Kelvin s’était posé cette question au XIXème siècle, et avait proposé sa solution : pour lui, le meilleur pavage est celui qu’on obtient avec l’octaèdre tronqué. Comme le montre l’image ci-contre, il s’agit d’un volume possédant 14 faces dont 8 hexagones et 6 carrés. Toutefois Kelvin n’a pas su montrer que cette forme était la meilleure, mais il croyait ferme à son résultat : cette affirmation est donc devenue la conjecture de Kelvin. Le pavage qui en résulte est représenté dans l’image d’en-tête de ce billet.
Le physicien britannique Lord Kelvin s’était posé cette question au XIXème siècle, et avait proposé sa solution : pour lui, le meilleur pavage est celui qu’on obtient avec l’octaèdre tronqué. Comme le montre l’image ci-contre, il s’agit d’un volume possédant 14 faces dont 8 hexagones et 6 carrés. Toutefois Kelvin n’a pas su montrer que cette forme était la meilleure, mais il croyait ferme à son résultat : cette affirmation est donc devenue la conjecture de Kelvin. Le pavage qui en résulte est représenté dans l’image d’en-tête de ce billet.
Mais pour trouver la forme optimale en 3 dimensions, est-ce qu’on ne pourrait pas s’inspirer de ce que font les abeilles en 2 dimensions ? Eh bien si ! Et vous allez voir que pour cela il ne faut pas regarder du côté des abeilles, mais plutôt du côté de la bière !
Les mousses, des pavages en 3 dimensions
 Nous l’avons vu précédemment, une manière naturelle de trouver la forme hexagonale, c’est de partir de cercles juxtaposés que l’on déforme. Si on veut faire pareil en 3 dimensions, on peut partir de sphères juxtaposées, et les déformer pour qu’elles se touchent. Et c’est justement ce qui se passe dans une mousse !
Nous l’avons vu précédemment, une manière naturelle de trouver la forme hexagonale, c’est de partir de cercles juxtaposés que l’on déforme. Si on veut faire pareil en 3 dimensions, on peut partir de sphères juxtaposées, et les déformer pour qu’elles se touchent. Et c’est justement ce qui se passe dans une mousse !
En effet quand des bulles se forment dans un liquide, elles sont initialement sphériques. Puis elles se touchent et se déforment pour donner des polyèdres qui remplissent l’espace en essayant de minimiser leur surface. Donc pour savoir si Kelvin avait raison, allons donc observer des mousses.
C’est justement ce qu’a fait le botaniste Edwin Matzke en 1946 : il a fabriqué quelques litres de mousse dont les bulles possédaient toutes le même volume, et il a observé au microscope la forme des bulles. Et parmi les milliers de bulles ainsi examinées, il n’en a pas trouvé une seule ayant la forme de l’octaèdre tronqué de Kelvin ! Au contraire, il a noté que les bulles possédaient 13 ou 14 faces, et le plus souvent des faces pentagonales, alors que l’octaèdre tronqué ne possède que des hexagones et des carrés. Il a ensuite fallut attendre 1955 pour qu’un autre botaniste, John Dodd, parvienne à faire la première photo d’une bulle ayant la forme de Kelvin !
Bref, Kelvin a peut-être proposé une forme optimale, mais contrairement au nid d’abeille, la nature ne semble pas très pressée de l’adopter ! L’argument mécanique proposé par Xochipilli pour les nids d’abeilles ne semble donc pas fonctionner en 3 dimensions !
Le contre-exemple de Weaire-Phelan
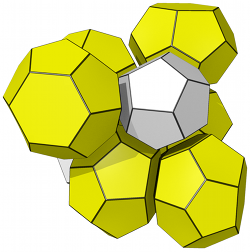 En 1994, les choses en étaient toujours là quand – coup de théatre ! – le physicien irlandais Denis Weaire et son étudiant Robert Phelan finissent par trouver un contre-exemple à la conjecture de Kelvin. Ils ont en effet trouvé un pavage possédant une surface plus petite que celle avec l’octaèdre tronqué de Kelvin. L’amélioration n’est pas démentielle, seulement 0.3%, mais ça montre quand même que Kelvin avait tort !
En 1994, les choses en étaient toujours là quand – coup de théatre ! – le physicien irlandais Denis Weaire et son étudiant Robert Phelan finissent par trouver un contre-exemple à la conjecture de Kelvin. Ils ont en effet trouvé un pavage possédant une surface plus petite que celle avec l’octaèdre tronqué de Kelvin. L’amélioration n’est pas démentielle, seulement 0.3%, mais ça montre quand même que Kelvin avait tort !
Voyons un peu la forme trouvé par Weaire et Phelan, ou plutôt les formes, car leur pavage est composé de 2 éléments de volume identique : l’un possède 12 faces et l’autre 14, les faces étant des hexagones ou des pentagones.Vous pouvez admirer ci-contre la structure correspondante.
A ce jour, Weaire et Phelan détiennent toujours le record, mais il n’existe toujours pas de preuve mathématique que cette structure soit la meilleure possible. D’ailleurs les recherches continuent, et un jeune chercheur italien, Ruggero Gabbrielli, a récemment réussi à trouver un autre contre-exemple, moins bon que Weaire-Phelan mais quand même meilleur que Kelvin. Au début de l’année 2012, il a également réalisé expérimentalement la première mousse de Weaire-Phelan.
Enfin cet étrange objet mathématique inspire aussi les designers, puisque le Water Cube, la piscine des Jeux Olympiques de Pékin en 2008, a été réalisé sur le modèle de la structure de Weaire-Phelan !
Pour aller plus loin…
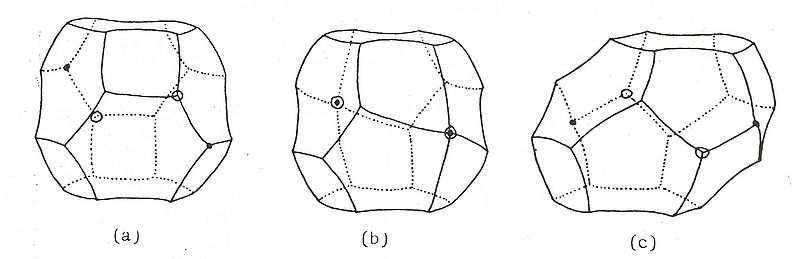
Suite aux investigations de Matzke dans les mousses réelles, plusieurs chercheurs se sont demandés pourquoi la bulle en forme de cellule de Kelvin était si rare, alors qu’elle est censée être optimale. En 1961, Williams a proposé une explication : il a construit un autre polyèdre à 14 faces (on dit un tetrakaidecaèdre) qui est une variante de celui de Kelvin, et qui possède des faces pentagonales. Cette cellule de Williams semble être la forme privilégiée qu’adoptent les bulles dans un mousse faite de bulles monodisperses. La transformation de la cellule de Kelvin à celle de Williams est donnée ci-dessous
Enfin l’histoire de la démonstration du théorème du nid d’abeille par T.Hales est assez intéressante. Ce dernier est également l’auteur de la première preuve de la conjecture de Kepler – dont je vous parlerai un autre jour – et qui porte sur la manière optimale d’empiler des sphères. Là aussi il s’agit d’un résultat très simple, mais la démonstration a du attendre des siècles. Et la preuve de T. Hales est absolument monstrueuse ! Elle s’étale sur 250 pages et 8 publications, traite plus de 5000 cas différents (dont un a nécessité une thèse entière), et fait un usage intensif de programmes informatiques dont les entrées et sorties totalisent 3 giga-octets de données. Le papier a été soumis en 1998 à Annals of Mathematics, et accepté seulement en 2005, après que les 12 réferrés aient décidé d’abandonner. Bref, une des démonstrations les plus ardues de l’histoire des mathématiques ! Après ce travail de titan, Denis Weaire conseille à Thomas Hales de s’intéresser à la conjecture du nid d’abeille. « Given its celebrated history, it seems worth a try. » lui dit-il. Hales s’imagine en reprendre pour 10 ans, et là suprise ! Il torche l’affaire en 6 mois et seulement 20 pages de démonstration ! Ce qui lui fait dire « In contrast with the years of forced labor that gave the proof of the Kepler Conjecture, I felt as if I had won a lottery. »







18 Comments
Beau sujet !
Note que cela concerne aussi les solides poreux (mousses polymères, os, bois…) et leur comportement mécanique en fonction de la porosité.
SG
Pingback: Du théorème du nid d’abeille à la conjecture de Kelvin | C@fé des Sciences | Scoop.it
Pingback: Du théorème du nid d’abeille à la conjecture de Kelvin | gpmt | Scoop.it
Si la structure de Kelvin est difficile à observer dans les mousses, c’est notamment parce qu’il est délicat de maintenir une mousse où les bulles restent de volume parfaitement égal: entre l’eau qui coule vers le bas, le gaz qui passe des petites bulles vers les grosses et les films de savon qui cassent, la « mousse parfaite » ne tient pas longtemps… maintenant on y arrive en faisant de toutes petites bulles (Crystalline arrangements of microbubbles in monodisperse foams, van der Net et al., 2007… où l’on voit la mousse passer de Kepler à Kelvin suivant la quantité d’eau !).
La structure de Weaire-Phelan pose encore plus de problèmes, parce qu’elle ne peut pas s’appuyer sur un plan. Pour l’observer, il a fallu aider un peu la mousse en la posant dans un récipient dont les parois sont un « moule » de la bonne structure.
Très chouette, merci pour la reference du papier ! Je l’ai trouvé là : http://www.maths.tcd.ie/~garyd/Publications/vanderNet_2007_ColSurfA_Crystalline_Microbubbles.pdf
Le 26 novembre 2012 12:04, Science étonnante
Fascinant, je ne connaissais pas l’histoire de l’optimalité en 3 dimensions.
Et en trois dimensions ? Le problème de Kelvin.
La solution optimale au problème de Kelvin : est un tétradécaèdre constitué de faces pentagonales dans les proportions suivantes : quatre côtés de valeur égale et un cinquième de 0.6 (le 6 est souligné) par rapport à la valeur initiale des autres ; cela équivaut à 56 côtés de valeur x pour 14 côtés de valeur 0.6 (le 6 est souligné) de x.
Cela m’a pris cinq minutes à trouver, mais je n’ai pas les moyens de prouver ce schéma par une construction graphique de celui-ci. Mais en rentrant ces données dans un logiciel adéquat, le tétradécaètre idéal apparaîtra. La seule chose dont je sois sûr, c’est qu’il faut assembler quatorze tétradécaèdres dit « idéaux » pour en former un quinzième virtuel en leur centre comme pour la 2D où il fallait assembler six héxagones pour en trouver un septième virtuel en leur centre.
Bien à vous…
Pingback: Du théorème du nid d’abeille à la conjecture de Kelvin | Autour des maths | Scoop.it
Parce que je trouve ça super beau, on trouve aussi des hexagones dans la nature dans certains orgues volcaniques : http://apiculture-populaire.com/img/hexagone-basalte.jpg
D’après mes souvenirs de géologie, l’explication est liée à ce que tu racontes : l’hexagone minimise le périmètre pour la surface, et c’est important pour la dissipation d’énergie lors du refroidissement du magma ou un truc comme ça… A vérifier !
Pingback: rafax | Pearltrees
Moi j’ai acheté des carreaux fractaux pour ma salle de bain. Merveilleux à première vue, les interstices entre les carreaux se comblent au fur et à mesure et pratiquement pas besoins de coulis! Toutefois, le prix aussi est fractal: le commercant ne te facture pas tout de suite, parce que, c’est un Euro de base, puis ensuite, 1,10 Euro, etc, etc, à la fin la facture était salée!! Par chance que ce sont des carreaux en deux dimension seulement!!!
Pingback: Bulles de savon géantes ! | Science étonnante
Fastoche : http://gregegan.customer.netspace.net.au/APPLETS/19/19.html
Pingback: Abeille Math | Pearltrees
Je suis architecte et en 1983 j’ai fait des recherches sur les bulles de savon. je cherchais à créer une résille qui reprenait les caractéristiques angulaires des faces créées entre les bulles (planes si les bulles sont de même taille). J’ai finalement trouver le volume du dodécaèdre rhomboïdal (douze faces en losange) qui permet de remplir totalement l’espace avec une seule forme de base.
C’est aussi la forme qu’adopte le cristal de grenat almandin. Je ne serait pas surpris que ce volume fasse mieux que celui de Kelvin, mais je ne suis pas mathématicien…
Pingback: TPE abeille | Pearltrees
Pingback: Puzzle du nid d’abeille — Pixees
un grand merci