Les intégrales de Borwein sont une petite curiosité mathématique, mais qui sous des dehors inoffensifs peuvent nous faire réfléchir l’idée de démarche scientifique.
Voici le problème : on s’intéresse aux intégrales de la forme suivante, définies pour chaque nombre entier positif n:
A priori rien de très barbare dans cette formule, rien de passionnant non plus. Là où ça devient intriguant, c’est quand on commence à calculer explicitement la valeur de l’intégrale pour différentes valeurs de n.
Commençons avec n=0, on trouve
\(I_0 = \int_0^{+\infty} \frac{\sin x}{x} dx = \frac{\pi}{2}\)
Prenons maintenant n=1, ça donne
\(I_1 = \int_0^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{(x/3)} dx = \frac{\pi}{2}\)
Puis n=2, on a
\(I_2 = \int_0^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{(x/3)}\frac{\sin (x/5)}{(x/5)} dx = \frac{\pi}{2}\)
et n=3,
\(I_3 = \int_0^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{(x/3)}\frac{\sin (x/5)}{(x/5)} \frac{\sin (x/7)}{(x/7)} dx = \frac{\pi}{2}\)
et n = 4,
\(I_4 = \int_0^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{(x/3)}\frac{\sin (x/5)}{(x/5)} \frac{\sin (x/7)}{(x/7)}\frac{\sin (x/9)}{(x/9)} dx = \frac{\pi}{2}\)
Bref, pas besoin de vous faire un dessin, vous remarquez qu’on trouve toujours \(\pi/2\).
A ce stade, un bon physicien va continuer à calculer les intégrales pour n=5, peut-être pour n=6, puis il va énoncer la loi universelle que pour tout entier n, on a \(I_n = \pi/2 \). Il fera un joli papier, données expérimentales à l’appui, et affichera un degré de confiance de 99.9999%.
Le bon mathématicien, lui, va conjecturer que pour tout n \(I_n = \pi/2 \), et va se lancer dans la recherche d’une démonstration du résultat général.
Le bon informaticien va commencer à écrire un code lui permettant de calculer numériquement les intégrales, afin de vérifier la conjecture jusqu’à une valeur d’au moins \(n=2^{128} -1\). Suivons donc les tribulations de notre informaticien.
Il lance donc son calcul pour n=5, il trouve :
\(I_5 = 1.57079632679\)
c’est-à-dire \(\pi/2\) à 11 décimales près.
Il lance ensuite le calcul pour n=6, et il sort :
\(I_6= 1.57079632679\)
Idem. Tout va bien. Il passe à n=7, et là :
\(I_7= 1.57079632677\).
On dirait que la 11ème décimale diffère ! Bon c’est presque \(\pi/2\) quand même. On peut calculer numériquement que c’est en fait \(0.49999999992\pi\). L’informaticien conclut que c’est une erreur d’arrondi dans son algorithme. Le physicien lui, aurait conclu à une erreur de mesure expérimentale.
Et pourtant pas de bol, pendant ce temps le mathématicien s’acharne sur l’intégrale numéro 7, et fini par démontrer qu’elle ne vaut pas \(\pi/2\), mais très exactement :
\(I_7 = \frac{467807924713440738696537864469}{935615849440640907310521750000} \pi\),
ce qui est presque \(\pi/2\), mais pas tout à fait !
La conjecture est donc fausse ! Pour les valeurs de n supérieures à 7, l’intégrale se met à s’éloigner de plus en plus de la valeur de \(\pi/2\) ! Étonnant, non ?
Morale de l’histoire, il est parfois dangereux de généraliser trop vite des premiers résultats numériques ou expérimentaux !
Pour aller plus loin : le papier des frères Borwein et de R. Baillie dans lequel cette surprise mathématique a été rapportée en 2007.
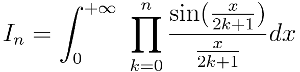



12 Comments
Très mignon ! Il y a longtemps que je ne sais plus calculer des intégrales, mais ces rapports magiques entre nombres sont fascinants. Les intégrales de Borwein ont-elles un sens particulier, une raison d’être ?
Très bonne question ! 🙂
Je n’ai pas développé parce que 1. j’avais la flemme de chercher à comprendre 2. j’aurai eu la flemme d’écrire les explications.
Mais quand même :
Si j’ai bien compris, elles donnent en quelque sorte le volume d’une figure géométrique (genre un polyèdre) et toujours si j’ai bien compris, en faisant changer les facteurs qui sont dans les sin, on modifie le domaine d’intégration et donc si on calcule bien « tout » le volume ou pas.
Apparemment il y a une sorte de règle qui dit que si la somme des inverses des facteurs dans les sin est
plus petite que 2, on a bien tout le volume d’intégration (et on a bien toujours pi/2), alors que si elle est plus grande on en rate une partie et on trouve moins que pi/2.
et comme tant que n est plus petit que 6 on est en dessous de 2, et que dès que n=7 on est supérieur à 2, c’est là que le changement intervient :
http://www.wolframalpha.com/input/?i=sum++for+k+from+0+to+7+of+1%2F%282*k%2B1%29
Pingback: Les intégrales de Borwein | C@fé des Sciences | Scoop.it
Ca fait un peu la blague de l’américain, du belge et du français tout ça ^^
Plus sérieusement, c’est pour ça que les domaines sont complémentaires. Par contre il faut relativiser il a certaines technologies que les mathématiques n’arrivent pas à expliquer/démontrer et que l’on peut utiliser grâce à des simulations informatiques et des expériences en physique.
(Bon y’a un léger conflit d’intérêt dans mon post puisque je suis plutôt ingénieur/physicien)
Intéressant comme petite morale pour cette démonstration mathématique. 🙂
Mais, j’ai une question qui n’est vraiment en lien avec le sujet de cet article, comment faites vous pour inclure des formules mathématiques ?
L’utilisation du bon physicien, du bon mathématicien et du bon informaticien me fait penser à la blague (et ses multiples variations/extensions) sur l’étude de l’assertion « tous les nombres impairs à partir de 3 sont premiers » ^^.
Bien observé ! C’était effectivement un clin d’oeil à cette blague !
L’auteur a dissimulé dans son blog, sans doute délibérément, un autre exemple que nos neurones nous pousse à généraliser.
En lisant les informations sur les auteurs dans l’article cité, j’ai été étonné de la date d’obtention des diplômes des « frères Borwein ».
Bien que les frères Jonathan et Peter Borwein ont cosignés des travaux en mathématique, les intégrales de Borwein sont l’œuvre de David et Jonathan, père et fils !!
Ah ben non je n’avais pas vu ! Moi aussi j’avais généralisé abusivement !
Bien vu et merci !
Pingback: La deuxième conjecture de Hardy-Littlewood | Science étonnante
En langue espagnole;
http://lit-et-raire.blogspot.com.es/2013/02/una-sucesion-muy-natural-y-tu-medida.html
Voici pour les plus courageux une explication probabiliste du résultat
https://www.concours-centrale-supelec.fr/CentraleSupelec/2016/MP/sujets/2012-005.pdf