 Le problème de Monty Hall est un célèbre jeu de probabilités qui tire son nom d’une émission télévisée. On le qualifie de paradoxe, car la bonne stratégie à adopter nous semble souvent contre-intuitive.
Le problème de Monty Hall est un célèbre jeu de probabilités qui tire son nom d’une émission télévisée. On le qualifie de paradoxe, car la bonne stratégie à adopter nous semble souvent contre-intuitive.
Des expériences montrent d’ailleurs que même en répétant plusieurs fois le jeu, l’être humain a vraiment du mal à comprendre le truc, alors que le pigeon, lui, s’en sort très bien.
De là à conclure à la supériorité intellectuelle des volatiles, il n’y a qu’un pas !
Le principe du jeu
 Le paradoxe de Monty Hall trouve son origine dans le jeu télévisé Let’s Make a Deal, diffusé aux Etats-Unis à partir de 1963. L’animateur Monty Hall y proposait le choix suivant.
Le paradoxe de Monty Hall trouve son origine dans le jeu télévisé Let’s Make a Deal, diffusé aux Etats-Unis à partir de 1963. L’animateur Monty Hall y proposait le choix suivant.
Un candidat est présenté face à 3 portes : derrière une seule de ces portes se trouve un cadeau, alors que derrière chacune des deux autres portes se trouve un objet sans intérêt (typiquement : une chèvre).
- Le candidat choisit une de ces 3 portes, mais sans l’ouvrir;
- L’animateur (qui sait où se trouve le cadeau) ouvre une des 2 portes restantes, en prenant soin (si besoin) d’éviter la porte qui contient le cadeau (la porte ouverte par l’animateur révèle donc toujours une chèvre);
- Le candidat a alors le choix entre conserver sa porte initiale, ou changer pour pour prendre l’autre porte restante.
Que doit faire le candidat ? Conserver ou changer ?
Réfléchissez donc 5 minutes…
Une chance sur deux (ou trois)
En faisant un raisonnement rapide, on peut se dire qu’on a le choix entre deux portes, et qu’initialement chaque porte a autant de chance que l’autre de contenir le cadeau. Alors que l’on change ou que l’on conserve sa porte, on gagne avec une chance sur deux.
En réalité ce raisonnement est trompeur, et le vrai résultat est que la probabilité de gagner si on change est de 2/3 contre seulement 1/3 si on conserve sa porte initiale : on a donc toujours intérêt à changer !
On peut passer des heures à essayer de se convaincre de ce résultat. Voici l’argument le plus simple : si vous restez, vous gagnez si vous aviez au départ fait le bon choix (ce qui se produit dans un tiers des cas), si vous changez, vous gagnez si vous aviez fait au départ le mauvais choix (ce qui se produit 2 fois sur 3). Donc changer vous fait gagner dans 2/3 des cas.
Pour les sceptiques, la méthode la plus définitive consiste à dénombrer tous les cas, voire à faire une simulation numérique (on raconte que le mathématicien Erdös dû faire cette simulation pour se laisser convaincre du résultat). Pour les sceptiques n’aimant pas les méthodes de physicien, la solution avec des probabilités bayésiennes.
Un problème pour pigeons ?
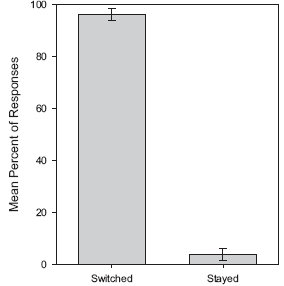 Pour quelqu’un qui découvre le jeu, une manière de trouver la bonne tactique, c’est de jouer une centaine de parties. On peut penser que si vous êtes un peu observateur, vous allez finir par comprendre que changer est en moyenne plus intéressant que rester.
Pour quelqu’un qui découvre le jeu, une manière de trouver la bonne tactique, c’est de jouer une centaine de parties. On peut penser que si vous êtes un peu observateur, vous allez finir par comprendre que changer est en moyenne plus intéressant que rester.
D’ailleurs le pigeon lui fait ça très bien. C’est l’expérience qu’ont réalisé deux chercheurs en psychologie du Whitman College dans l’état de Washington (*). Ils ont soumis plusieurs volatiles à une version répétée du problème Monty Hall (où le cadeau c’est de la bouffe, car le pigeon est basique).
Ils ont alors observé qu’après plusieurs centaines d’essais, le pigeon a parfaitement compris que la bonne stratégie c’est de changer. Au début de l’expérience ils changent de porte dans 36% des cas, alors qu’à la fin de l’expérience (qui dure plusieurs jours), ils changent dans 96% des cas ! (voir ci-contre)
Homme VS Pigeon
 Là où ça devient inquiétant, c’est qu’en soumettant des humains à la même version répétée du problème, ils ont observé que l’homme ne semble pas très enclin à apprendre de ses erreurs : après 200 essais les humains ne changent que dans 66% des cas. Le pigeon bat l’homme sans problèmes !
Là où ça devient inquiétant, c’est qu’en soumettant des humains à la même version répétée du problème, ils ont observé que l’homme ne semble pas très enclin à apprendre de ses erreurs : après 200 essais les humains ne changent que dans 66% des cas. Le pigeon bat l’homme sans problèmes !
Il faut croire que dans cette situation, l’homme est pollué par son propre (mauvais) raisonnement, et continue de penser que changer ou pas, ça ne fait pas de différence.
En attendant, le pigeon, lui, se gave…
L’article :
(*) Walter T. Herbranson and Julia Schroeder, Are Birds Smarter Than Mathematicians? Pigeons (Columba livia) Perform Optimally on a Version of the Monty Hall Dilemma, Journal of Comparative Psychology (2010), Vol. 124, No. 1, 1–13.
Vous pouvez y lire en détail la manière dont on peut faire jouer un pigeon au problème de Monty hall avec des portes, des lumières et de la nourriture.




38 Comments
Bonjour,
Merci pour cet article étonnant.
J’ajouterais qu’un moyen simple de se convaincre de la justesse du raisonnement est d’imaginer qu’on a un grand nombre de portes (mettons 1 million) et que le cadeau ne se trouve que derrière l’une d’elle. Le candidat choisit une porte et l’animateur en ouvre 999.998 autres derrière lesquelles il sait qu’il ne se trouve pas, laissant simplement la porte choisie par le candidat et une autre porte. Conserveriez-vous votre choix ou choisiriez-vous l’autre porte ?
Personnellement, mon choix est vite fait. 🙂
Très bonne façon de faire comprendre Cylixte, assurément on change immédiatement.
Alors là je suis sur les fesses, cela fait près de 4 heures que ma compagne et moi même nous triturons le cerveau pour comprendre ce paradoxe, après plusieurs recherches sur la toile, impossible de trouver une réponse qui nous permette d’appréhender ce problème sereinement, c’est tellement contre-intuitif que même des statisticiens se sont apparemment cassés les dents dessus, et là Cylixte, en deux phrases nous permet de résoudre l’énigme. La démonstration est tout simplement excellente, car complètement intuitive ! Génial ! Un grand merci et félicitations !
J ai toujours pas compris pourquoi….je suis c..ou quoi ?
Contre-intuitif convient en effet très bien pour caractériser cette stratégie ! Très intéressant, cet article 🙂
excellent paradoxe !
Plus simple pour comprendre : au premier tirage, on a 2 chances sur 3 de choisir l’une des mauvaises cartes. L’animateur élimine l’autre. Reste la carte gagnante. En changeant systématiquement, on a donc 2 chances sur 3 d’être gagnant. Si on ne change pas, on a plus qu’une chance sur 3 de gagner.
Très bon le coup du pigeon… comme quoi l’apprentissage non supervisé, y a que ça de vrai.
Je connaissais le paradoxe de Monty Hall (ici, avec la variante des trois prisonniers), mais pas l’expérience des pigeons. Incroyable! Il me semble que ça illustre parfaitement notre difficulté -très humaine- à reconnaître que son premier choix n’a pas été le bon, même lorsqu’il est évident qu’on a intérêt à l’admettre. C’est « l’effet des fonds perdus » (sunk cost effect) qui nous pousse à persévérer dans nos stratégies perdantes au motif de ce qu’on y a déjà pas mal investi (voir ce billet). Biais irrationnel qui n’a été repéré jusqu’ici ni chez les animaux ni chez les enfants en bas âge…
Pour l’effet de ‘sunk cost’, il semblerait quand même qu’il puisse en exister aussi des versions animales ! Je pense en faire le sujet d’un prochain billet…si tu es curieux, tu peux regarder ce papier
En ce qui concerne le paradoxe dans sa version ‘prisonnier’, je le trouve un peu moins paradoxal justement, peut être du fait qu’on a aucune décision à prendre, donc on ne voit pas bien comment nos chances de survie peuvent automatiquement augmenter sans qu’on ne fasse rien.
oui c’est bien à cet article que je fais référence dans mon billet 😉
Impressionnant.
J’avais consacré trois pages de mon premier ouvrage « Les indispensables mathématiques et physiques » (2006) à ce « paradoxe » qui m’avait fasciné (chapitre 10 « Incertaines probabilités »).
Parmi les explications que j’avais données, j’en mentionne une : une contrainte s’impose au jeu quand il dévoile une porte – car en aucun cas ce ne peut être la porte du salut.
L’apprentissage par les pigeons est étonnant.
Bonjour,
Je viens souvent sur ce site, mais bon, je franchit le pas !
Très intéressant, cet article ! On savais les pigeons critiques d’art, mais mathématicien, chapeau !
Remarque, ce paradoxe a largement été utilisé pour montrer les probabilités au grand public (ça marche à chaque fois), même NUMB3RS en a parlé.
Je fais juste un petit lien à l’article de ElJj : http://eljjdx.canalblog.com/archives/2007/01/20/3743059.html. Comme ça, vous êtes quitte !
Pingback: L’humain, moins bon en probabilités que les pigeons? » OwniSciences, Société, découvertes et culture scientifique
Mais à partir du moment où une des trois portes a été ouverte, ne doit-on pas raisonner avec une probabilité basée sur seulement deux portes, bref repartir à zéro ?
Deux portes effectivement (celles non montrées par le présentateur). Mais pas une probabilité uniforme. Il y a plus de chance que l’objet convoité soit derrière l’une de ces deux portes.
Pingback: L’humain, moins bon en probabilités que les pigeons? » OWNI, News, Augmented
Pingback: Le singe, un homo économicus irrationnel comme les autres « Science étonnante
Pingback: Le paradoxe de Monti-Hall révélé ! |
Pingback: >Irrationalités animales | Le Webinet des Curiosités
Non je croit pas les probabilité 2/3 gagnant contre 1/3 en changeons de porte hhh, c’est une probabilité truquer (diriger par une improbabilité) : regarder mon point de vu : http://www.fichier-pdf.fr/2012/12/11/monty-hall/
1) le systeme est a trois case donc au 2ieme coup la probabilité est a 2/3 mais comme le premier coup est un indicateur qui fausse les probabilité elle méme , la probabilité est re-équilibré dans le systeme à 3 case par une probabilité de 1/2 qui corespond au final au systeme indépendant a 2 cases.
j’ai coriger deux trois phrase du 1 er pdf (c’est un truc oral populaire mais les base de la démonstration est suffisante): http://www.fichier-pdf.fr/2012/12/12/monty-hall/
bon pourquoi vous acusez l’émission de tele !? faut pas non plus dire que le principe du jeux monty hall ne fonctione pas ! les 2/3 contre 1/3 si il ne change pas de case est facile a comprendre et c’est vrai puisque le choix initial du candidat se fait dans l’ensemble des n cases du systeme alors que le gain est ramener progréssivement par le présentateur dans l’ensemble des 2 cases restantes donc la probabilité que la case choisi par le candidat soit la bonne est de 1/n et forcément la 2ieme case a la probabilité (n-1)/n . c’est des problemes différent , tout dépend des conventions initial…
Bonjour.
Malgré toutes les « preuves » présentées, j’ai beaucoup de mal à accepter les conclusions de ce paradoxe. Les pigeons sont peut-être plus forts que moi, mais il n’empêche que ma logique ne s’y retrouve pas. Si vous le voulez bien, je vais essayer d’argumenter sans faire appel aux mathématiques car mon niveau ne me le permets pas.
Supposons donc qu’au départ on a fait le bon choix. On a choisi, par exemple, la porte du milieu, appelons-là « porte 2 ». On avait en effet une chance sur trois de faire ce bon choix. Et donc on avait deux chances sur trois de faire un mauvais choix, c’est-à-dire de choisir la porte 1 ou la porte 3.
A présent, l’animateur ouvre l’une des deux autres portes, laquelle nous montre une chèvre. En quoi est-ce que cela influe sur les probabilités de gagner le cadeau si, à partir de ce moment-là, on décide soit de conserver notre choix initial, soit d’en changer ? On nous dit qu’en changeant de choix on a soudain 2 chances sur 3 de gagner alors qu’à l’étape d’avant on n’en avait qu’une seule. Je pense qu’à ce moment-là, puisqu’il ne reste plus que deux portes en jeu, la probabilité de gagner est maintenant de 1 chance sur 2. Changer ou ne pas changer de choix à ce moment-là ne peut pas avoir plus d’incidence sur cette probabilité que ça n’en avait avant que la porte 3 (la porte à la chèvre) soit ouverte. Dans le cas où j’aurais fait le bon choix dès la première étape, en changer à partir de ce moment me ferait perdre. N’en pas changer me ferait gagner. Il n’y a bien que deux possibilités, donc 1 chance sur 2 et non pas 2 sur 3. Je ne comprends pas du tout la validité du raisonnement qui fait intervenir au moment de la 2ème étape les probabilités telles qu’elles existaient à la 1ère étape. Vous nous dites que des simulations montrent sa validité, mais je suis moyennement disposé à croire les résultats de ces simulations faites par d’autres si elles contredisent un raisonnement qui me semble tout de même beaucoup plus correct que celui que vous avancez.
Vous insérez un lien vers un article de Wikipédia qui présente une démonstration à l’aide du théorème de Bayes. Etant donné mon niveau de maths je suis obligé de l’admettre sans discussion. Pourtant, je voudrais quand même discuter quelque chose dans cette démonstration.
Vous écrivez :
• Soit la voiture est derrière la porte 1 : le présentateur ouvrira la porte 2.
• Soit la voiture est derrière la porte 2 : le présentateur ouvrira la porte 1.
• Soit la voiture est derrière la porte 3 : le présentateur ouvrira la porte 1 ou le présentateur ouvrira la porte 2 (équiprobabilité 1/2)
Pour moi, sans utiliser le théorème de Bayes, cela veut dire que les probabilités d’ouverture des portes 1 et 2 sont égales. Dans ma position de joueur, il n’y a que deux possibilités : 1) la voiture est derrière la porte 3 (celle que j’ai choisie), donc équiprobabilité de 1/2 pour les deux autres portes ; ou 2) la voiture n’est pas derrière la porte 3, et il y a la même équiprobabilité de 1/2 pour les deux autres portes. Ce que je veux dire c’est que les deux premières possibilités n’en font en réalité qu’une seule du point de vue du joueur ; peu importe de nommer les portes, elles sont équivalentes, et il n’est pas du tout pertinent de les faire intervenir séparément dans une formule mathématique qui n’est peut-être (ce n’est qu’une supposition de ma part) pas utilisée à bon escient ici.
Quelque part dans cet article de Wikipédia, l’auteur écrit ceci :
« Le présentateur ouvre maintenant la porte 1. Bien sûr le présentateur n’ouvre jamais une porte donnant sur la voiture, donc sans surprise la porte 1 donne sur une chèvre ce qui a pour effet de transférer la probabilité de 2/3 de chances d’avoir une voiture non plus sur les portes 1 et 2 comme expliqué précédemment, mais uniquement sur la porte 2 (voir graphique ci-dessous).
De manière encore plus simple, on peut reformuler en disant que si après le choix initial du candidat il était envisageable que la voiture se trouve derrière les portes 1 et 2 (avec une probabilité de 2/3), ce n’est plus le cas après l’ouverture de la porte 1 par le présentateur : seule la porte 2 est encore susceptible de cacher la voiture (et par conséquent, toujours avec une probabilité de 2/3) ».
Je conteste ce qu’il appelle ici le « transfert de la probabilité ». Comme je l’ai dis plus haut, il n’y a aucune raison de faire intervenir au moment de la 2ème étape les probabilités telles qu’elles existaient à la 1ère étape, c’est-à-dire en d’autres termes, aucune raison de « transférer » les probabilités de la première à la deuxième. Pour moi, dès que le présentateur ouvre une porte, on se retrouve dans un autre problème avec ses propres probabilités. D’ailleurs on pourrait très bien considérer que la première partie du problème n’existe pas. On se trouverait alors devant un problème qui s’énonce de la manière suivante : Le joueur est devant trois portes. L’une est ouverte et l’on voit une chèvre derrière. Une voiture est cachée derrière l’une des deux autres portes. Quelles sont les probabilités pour qu’elle soit derrière la porte 1 ou la porte 2 ? Il est clair qu’elles sont de 1/2 et qu’il n’y a aucune raison de faire intervenir des probabilités résultant d’un « premier choix » qui n’a pas eu lieu.
Certains disent que ce qui modifie les probabilités, c’est qu’en ouvrant une porte qui n’est pas la bonne, le présentateur nous donne une information supplémentaire. Mais qu’elle est donc cette information supplémentaire ? Nous savions déjà que deux portes sur trois n’étaient pas les bonnes, et à partir du moment où nous en avions choisi une, cela revenait à éliminer les deux autres (pardonnez-mois d’enfoncer des… portes ouvertes). Le présentateur confirme juste que nous avons eu raison d’en éliminer une sur ces deux-là, mais cela ne nous donne aucune information supplémentaire. On se doutait bien déjà qu’en en éliminant deux, il y en avait forcément au moins une qu’on avait raison d’éliminer. Que ce soit celle-ci ou celle-là, la 1 ou la 2, la A ou la B, ça ne nous apporte rien de plus. Il nous reste toujours à choisir entre les deux restantes, et toujours avec une chance sur deux.
Il reste la démonstration par les pigeons. Comme Je n’ai guère plus le courage de me taper la traduction d’une description d’expérience que d’une démonstration de mathématiques, il me reste à supposer que cette expérience a été critiquée et peut-être réfutée. Bref ! Est-ce qu’elle montre bien ce qu’on croit qu’elle montre ? Pardonnez-moi de tout mettre en doute, mais entre mon raisonnement et des « faits » qu’on me présente et que je n’ai pas la possibilité de vérifier, je préfère mon raisonnement.
amicalement,
henri
« Le joueur est devant trois portes. L’une est ouverte et l’on voit une chèvre derrière. Une voiture est cachée derrière l’une des deux autres portes. Quelles sont les probabilités pour qu’elle soit derrière la porte 1 ou la porte 2 ? Il est clair qu’elles sont de 1/2 et qu’il n’y a aucune raison de faire intervenir des probabilités résultant d’un « premier choix » qui n’a pas eu lieu. »
ici c’est bien 1/2 contre 1/2 mais dans le monty hall le candidat fait son 1er choix avant que la porte soit ouverte sur la chèvre donc c’est 1/3 contre 2/3.
Mais ne serait-il pas plus protocolaire de choisir à nouveau au hasard entre les deux portes restantes ?
Oui Tosfot, dans le monty hall, le candidat fait son 1er choix avant que la porte soit ouverte sur la chèvre, et c’est en effet 1/3 contre 2/3. Mais ce que je dis, c’est qu’une fois qu’une des portes est ouverte on se trouve dans un autre problème où les probabilités sont de 1/2 et 1/2. Il n’y a aucune raison de conserver (ou de « transférer ») les probabilités du problème précédent qui n’a plus rien à voir.
Si le paradoxe a fait couler tant d’encre, c’est bien parce que c’est justement contre-intuitif ! Pour moi la méthode la plus simple pour se convaincre est de faire un arbre des cas. Il n’y a que deux éléments à considérer : j’ai choisit bon au départ ou pas (2 cas), puis j’ai décidé de changer ou pas (2 cas). Soit seulement 4 cas au total…Et Henri ton erreur est de dire que le problème n’a plus rien à voir avec le précédent, c’est justement dans ce genre de raisonnement apparemment bénin que réside le piège 🙂
Bon, j’ai compris où était mon erreur de raisonnement après avoir réfléchi à la variante à 100 portes. C’est vrai que tout devient lumineux dans ce cas de figure. A un certain moment il y a une espèce d’alerte qui s’allume dans votre cerveau et vous vous dites : « minute, là ! ». Dans cette variante, le présentateur va ouvrir 98 portes derrière lesquelles il n’y a aucune voiture. Celle-ci est donc derrière l’une des deux portes restées fermées, dont l’une est celle que vous avez choisie au hasard. Et c’est vrai que, dans l’absolu, il y une probabilité de ½ pour chaque porte. Mais c’est là que l’alerte s’allume dans votre cerveau, parce que ce n’est pas cette probabilité-là qu’il faut prendre en compte mais celle de votre choix initial. Celle-ci est de 1 chance sur 100, puisque toutes les portes étaient fermées à ce moment-là, et même le veinard le plus confiant dans sa chance doit se dire qu’il n’est pas possible qu’il ait pu deviner juste du premier coup sur 100 portes et qu’il a intérêt à changer d’idée. La voiture est forcément derrière l’autre porte, à 99 chances sur 100.
Alors maintenant, pourquoi cette alerte ne s’allume pas dans la variante à trois portes ? Une fois qu’une porte est ouverte, on confond les deux probabilités : celle que la voiture est nécessairement derrière une des deux portes fermées, donc ½, et celle de notre choix initial, qui est de 1/3, et qui implique 2/3 pour l’autre porte. C’est sans doute cette confusion à ne pas faire que vous vouliez exprimer en parlant de « transfert de probabilité », expression que je ne comprenais pas. Je comprends mieux en disant qu’il faut éviter de confondre deux probabilités qui ne portent pas sur la même chose, ou plutôt éviter de perdre de vue qu’elles ne portent pas sur la même chose. La probabilité de justesse de mon choix initial est de 1/3, celle que la voiture se trouve derrière la porte que j’ai choisie est de ½ (une fois qu’une porte a été ouverte). Mais celle-ci il faut l’oublier, elle ne nous sert à rien, et même elle nous trompe.
Et alors pourquoi les pigeons font-ils mieux que nous ? Ce n’est certainement pas qu’ils font le bon raisonnement. C’est plutôt parce qu’ils ne font justement aucun raisonnement, n’ont aucune théorie des probabilités et ne risquent donc pas de confondre deux probabilités qui n’ont rien à voir l’une avec l’autre. Tout bêtement ils y vont « à l’aveugle », ils tâtonnent, et leurs essais et erreurs s’inscrivent dans leur mémoire. A la longue celle-ci finit par enregistrer quelle est la stratégie efficace et ils l’appliquent sans se poser de questions. Nous ne procédons pas ainsi parce que l’évolution a inscrit en nous une stratégie fondée sur une connaissance intuitive quoiqu’approximative des probabilités qui fonctionne mieux dans la plupart des cas que la stratégie tâtonnante. Le problème c’est que cette connaissance approximative n’est efficace que dans la plupart des cas mais pas dans tous, et c’est ici l’un de ces cas.
Ta démonstration m a convaincu. Merci
merci à tous pour cette explication d’un paradoxe qui m’aura valu une belle migraine….un merci spécial à Henri avec qui je me sentais en totale connexion (« waw il exprime exactement ma pensée !! ») mais la transposition avec les 100 portes: » Celle-ci est de 1 chance sur 100, puisque toutes les portes étaient fermées à ce moment-là, et même le veinard le plus confiant dans sa chance doit se dire qu’il n’est pas possible qu’il ait pu deviner juste du premier coup sur 100 portes et qu’il a intérêt à changer d’idée. La voiture est forcément derrière l’autre porte, à 99 chances sur 100. » …..je bute sur le « raisonnement » « je ne peux gagner du premier coup, ce serait trop invraisemblable »….est)ce un raisonnement ???, j’ai passé la journée à parcourir ce site et liens, je vais faire une pause, j’aurai peut-être une épiphanie cette nuit…..(me sens vraiment pigeon avec ces casse-tête…pire même si les pigeons y finissent par apprendre, à leur manière, faudrait peut-être que je subisse les mêmes tests qu’eux ??? :p)
Bonjour Gildor.
Eh bien il me semble que le fait de deviner juste du premier coup sur une probabilité de 1/100 est, sinon un raisonnement, du moins une sérieuse alerte à réviser votre raisonnement, comme je l’ai dit. C’est en quelque sorte une étincelle qui ne peut que vous inciter à penser que votre raisonnement était faux.
Bonjour, en fait « la pièce est tombée » chez moi en regardant une vidéo de Lazarus (allez savoir pourquoi alors que c’est très clair ici) qui reprenait exactement le même thème,bon j’avoue qu’ une partie de moi est toujours, disons, « troublée » ( ça crée de la dissonance et me fait me sentir bête, j’aime pas!!), il propose d’ailleurs sur son site de tenter l’expérience….en choisissant selon le raisonnement expliqué ici (qui restait pour moi théorique ), bref, cinq fois de suite j’ai eu la mauvaise porte lol —> »pas de chance » 🙂 mais je n’en tire pas de conclusions m’amenant à réfuter ce qui a été expliqué, loin de là 😉 d’ailleurs j’ai réessayé une série par la suite et là 8/10 ça a marché ^^
Désolé, j’ai posté trop vite, évidemment pour les 100 portes oui transposé en probs c’est ridicule de contester la logique, c’est la formulation qui m’a arrêtée alors qu’elle veut dire « peu probable que » et en effet….voilà, 😉
Pingback: [Vidéo] Les pigeons, rois des cons ? | | Science de comptoir - ISSN : 2270-4310
Pingback: Le jeu des 3 portes – Problème de Monty Hall – Bastien Faure
Moi, je prendrais la chevre
petit polisson va !
Pingback: Les pigeons, rois des cons ? - Qualitay.fr