 La fourmi de Langton est un petit programme informatique qui décrit une fourmi se déplaçant sur les cases d’une grille. Les règles qui régissent le mouvement de la fourmi sont d’une grande simplicité, et pourtant son comportement est complexe et tout sauf anodin. Et personne ne comprend vraiment pourquoi…
La fourmi de Langton est un petit programme informatique qui décrit une fourmi se déplaçant sur les cases d’une grille. Les règles qui régissent le mouvement de la fourmi sont d’une grande simplicité, et pourtant son comportement est complexe et tout sauf anodin. Et personne ne comprend vraiment pourquoi…
Les règles du jeu
Pour jouer à la fourmi de Langton (du nom de son créateur Chris Langton) il vous faut une feuille quadrillée, un crayon et une gomme. Au départ les cases de la grille peuvent être blanches ou noires, mais supposons pour commencer qu’elles sont toutes blanches. Mettez une petite flèche dans une des cases : ce sera votre fourmi, et l’orientation de la flèche indiquera sa direction.
A chaque tour, la fourmi se déplace selon les règles suivantes :
- Si la fourmi est sur une case blanche, elle effectue une rotation vers la gauche; si elle est sur une case noire, elle effectue une rotation vers la droite ;
- La fourmi inverse la couleur de la case sur laquelle elle se trouve (blanc devient noir et réciproquement);
- La fourmi avance d’une case dans la direction de son orientation.
Et on recommence. Facile, non ?
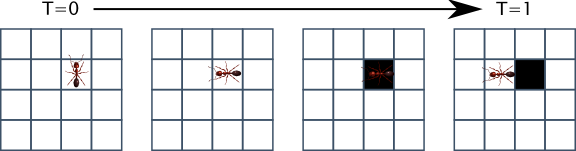
Voici ci-dessous un dessin du premier déplacement de notre fourmi : on part d’une configuration donnée (T=0) et on applique les 3 règles du mouvement : rotation, inversion de couleur et déplacement, et on termine dans la nouvelle configuration (T=1).
Si vous êtes courageux, prenez votre crayon et votre gomme, et faites avancer la fourmi 5 fois. Le résultat doit être semblable à celui ci-dessous.
Rassurez-vous pour la suite, en pratique on ne simule pas l’évolution de la fourmi avec un papier et un crayon, mais avec un (petit) programme informatique. Alors simulons notre fourmi et voyons ce qu’elle dessine avec les cases noires.
Les phases de la vie de la fourmi
A vue de nez, rien de bien enthousiasmant dans cette fourmi. Elle obéit à des règles très simples et on se dit que son évolution ne va pas être bien passionnante. Et pourtant, quand on la simule pendant quelques milliers de tours, il se passe des choses vraiment étonnantes.
En effet, la fourmi va passer par 3 phases vraiment très différentes, la phase « symétrique », la phase « chaotique » et la phase « autoroute ».
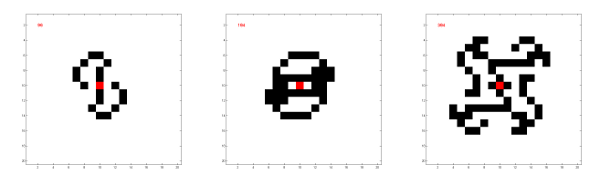
Au début de son évolution, la fourmi se balade dans une zone assez limitée de la grille, en dessinant des configurations régulières et symétriques. En voici quelques exemples (la fourmi est en rouge) :
Quand on voit ces figures, on peut penser que la fourmi de Langton va passer le restant de son existence à dessiner des jolies choses bien symétriques. Mais à partir de 500 tours, tout change. Elle se met à avoir un comportement chaotique, en élargissant son terrain de jeu et en créant des configurations très irrégulières.
Cette phase chaotique dure jusqu’à environ 10000 tours, et là le miracle se produit : la fourmi entame la construction d’une autoroute très régulière qui la conduit à l’infini.
Voyez par vous-même cette vidéo que j’ai réalisée et qui montre les 12 000 premiers tours. Observez bien la phase symétrique (jusqu’à 500), la phase chaotique (de 500 à 10000) et vous comprendrez vite à la fin de la vidéo ce que l’on appelle l’autoroute ! (attention la vidéo s’accélère au fur et à mesure)
[youtube=http://www.youtube.com/watch?v=i8N2xnMm6qE]
Le mystère de l’autoroute
L’autoroute est en fait un motif périodique de 104 pas qui se répète, et conduit au tracé que vous observez sur le film précédent. Personne ne comprend pourquoi elle apparaît et comment elle peut émerger du désordre qui caractérise la phase chaotique.
Ce qu’il y a de plus perturbant, c’est que même si on part d’une grille dont les cases sont coloriées aléatoirement en blanc ou en noir, l’autoroute finit toujours par apparaître un jour ou l’autre.
C’est encore un problème ouvert de démontrer que quelle que soit la configuration initiale, une autoroute apparaît (à moins de chercher un contre-exemple, mais aucun n’a été trouvé à ce jour).
Toutefois un pas intéressant a été franchi : on peut démontrer que la trajectoire de la fourmi est toujours non-bornée. C’est à dire que la fourmi finit toujours son parcours à l’infini…mais on ne sait pas montrer que c’est toujours via une construction d’autoroute !
Généraliser la fourmi
Il existe de nombreuses manières de généraliser le jeu de la fourmi de Langton. On peut bien sûr démarrer avec une grille dont certaines cases sont déjà noires. On peut modifier la topologie de la feuille, et jouer sur un tore au lieu d’un plan infini. On peut aussi changer la nature de la grille, triangulaire ou hexagonale par exemple. On peut également lancer plusieurs fourmis en même temps.
Une autre généralisation fascinante consiste à ajouter d’autres couleurs que le noir et le blanc. Si par exemple on ajoute le rouge, on doit définir la séquence des couleurs, par exemple blanc->noir->rouge->blanc, et la rotation associée à chaque couleur, par exemple blanc=gauche, noir=droite, rouge=droite. Mais on aurait aussi bien pu choisir rouge=gauche. Et ce choix peut être critique pour le comportement global de la fourmi !
Si on joue avec N couleurs, on a donc tout un tas de choix possibles (du genre 2^N) et tous ces choix peuvent conduire à des résultats très très différents. Un joli florilège dans la vidéo ci-dessous, qui montre que des règles en apparence très proches peuvent donner des comportements globaux très éloignés.
[youtube=http://www.youtube.com/watch?v=1X-gtr4pEBU]
A quoi sert la fourmi ?
La fourmi de Langton est un bel exemple de ce concept un peu flou que tout un tas de monde appelle l’émergence. Il s’agit en gros du fait qu’un système au comportement élémentaire simple peut donner lieu à un comportement global complexe. On retrouve cette idée en informatique, en physique, en biologie ou en sociologie.
La fourmi est donc une sorte de « forme de vie artificielle », à l’instar du jeu de la vie de Conway ou des automates cellulaires unidimensionnels de Wolfram, et dont on peut étudier le comportement pour essayer de comprendre comment des formes complexe peuvent émerger d’un système aux règles élémentaires si simples.
La fourmi de Langton n’a pas encore livré tous ses mystères !





29 Comments
Un peu de pub pour le langage Processing (http://processing.org) qui permet de faire rapidement des petites simulations sympas comme celle de la fourmi de Langton ( http://www.openprocessing.org/visuals/?visualID=1302 ), que j’ai confondu avec le Castor Affairé ( http://fr.wikipedia.org/wiki/Castor_affair%C3%A9 ), honte à moi.
Je trouve ca génial ! J’ai tout de même une question, on voit la création d’autoroutes dans le cadre d’un espace infini. Si on considère un espace fini dont les bords se rejoignent ainsi qu’un nombre de tours suffisamment important. Peut-on voir émerger une organisation supérieur, un motif se répliquant et se stabilisant comme dans le cas de l’autoroute ?
En fait même avec un espace fini dont les bords se rejoignent (c’est à dire un tore) l’autoroute finit par apparaître. Elle ne va pas à l’infini car elle se détruit quand elle revient sur la figure chaotique du centre, mais réapparaît toujours et ainsi de suite.
Ce motif en autoroute se comporte comme une sorte d’attracteur du système.
Une démonstration modifiable de la fourmi de Langton
Pour ceux que ça intéresse (je pense aux geeks de mon espèce), le principe de la fourmi est abordé dans un ouvrage fort sympathique, « la science du Disque-Monde » (donc écrit en partie par Terry Pratchett, que j’invite tout le monde à découvrir).
Au Passage,la preuve du fait que la fourmi est non bornée est très courte et assez facile.
Remarque 1.
On colorie l’espace avec un damier rouge/bleu. Il est facile de voir que si initialement, la fourmi est placée horizontalement sur une case bleue, alors lors de sa balade, elle sera toujours placée horizontalement sur les cases bleues et verticalement sur les cases rouges.
Preuve.
Supposons par l’absurde que la fourmie ne visite qu’un espace borné. Parmis les cases visitée un nombre infini de fois, il en existe une qui est la plus à gauche. Parmis celles qui sont les plus à gauche, il en existe une qui est la plus haute. Regardons cette case d’un peu plus près. Par symétrie, on peut suppose qu’elle est coloriée bleue. Elle ne va donc jamais rentrer dans cette case par le bas ou par le haut. Quitte à ne regarder qu’au bout d’un certain temps, elle ne rentre dans cette case que par la droite. Mais alors, une fois sur deux, quand elle rentre dans cette case, elle ressort dans la case immédiatement au dessus d’elle, ce qui contredit le choix initial de notre case. CQDF.
Pingback: Les automates cellulaires élémentaires | Science étonnante
Pingback: La fourmi de Langton et le concept d’émergence | Metaxu. Le blog de Philippe Quéau
Fantastique. J’avais déjà réflechi au sujet de l’émergence avec le « jeu de la vie », mais l’exemple d’une configuration unique qui emerge après la phase chaotique est tout simplement bluffant.
Merci pour la présentation et les vidéos. Cela dit, je suis un peu surpris que la compréhension du principe n’ait pas été trouvée rapidement ! En effet, il me semble que la réponse est contenue dans l’énoncé lui même, c’est à dire, le fait que l’ordre de marche de la fourmi est de tourner sur elle même, donc, de rester centré et non d’aller dans une direction aléatoire. Il n’y a pas de chaos issu de ce programme, même si cela y laisse penser. Ce qui me surprend le plus, c’est que tout le monde se laisse abuser par l’apparence, au lieu de s’en tenir à l’énoncé de la relation de causalité guidant la fourmi. Bon, il y a une astuce complémentaire, mais la simple observation suffit pour trouver la réponse, et une hypothèse à vérifier…
Si vous êtes intéressé, faites moi signe, je développerai, des fois que je me plante !
Je me pose une question et je sais pas si il y a des programmes pour le faire et à mon avis ça peut être intéressant, ce serrait de voir le résultat avec plusieurs fourmis sur l’échiquier
Oui il y a des vidéos sur le sujet sur Youtube !
Bonjour, j’ai quelques questions ! Serait-il possible de savoir où est-ce que tu t’es documenté pour ce billet ? Aussi, as tu un lien/référence où on trouve la démonstration du caractère non bornée de la trajectoire de la fourmi? Et enfin, t’es tu intéressé aux différents types de représentation (par exemple sur un graphe planaire) de la fourmi de Langton, et ses autres usages (Machine de Turing je crois)? Ah, et j’oubliais, j’ai essayé de lire quelques trucs sur l’émergence, mais la notion a l’air assez floue encore. As-tu des références claires à ce propos?
Merci d’avance pour ta réponse (Ou les réponses d’autrui !)
Bonjour,
J’ai l’impression que la phase « symétrique », dans le cas où les directives sont elles-même symétriques (case blanche, rotation à gauche / case noire, rotation à droite), correspond à une situation probable dépendante de la distance au point de départ (et donc du nombre de cases, qui représentent chacune une possibilité de ne pas pouvoir revenir au point de départ, le retour à celui-ci constituant une condition nécessaire au respect de la symétrie). Autrement dit, plus on avance dans le nombre de tours, plus l’automate s’éloigne de son point de départ et plus la probabilité devient faible qu’il puisse y retourner, du fait des motifs créés en chemin, qui constituent un risque de divergence.
Ensuite, lorsque la distance devient telle que la probabilité de revenir au point de départ est insuffisante et que la divergence se produit, le système semble se comporter comme un générateur aléatoire de variété.
Et le fait de voir finalement apparaître « l’autoroute » m’a fait faire le lien avec la loi de Godwin. Transposée ici, cela donnerait quelque chose du type : s’il existe un motif tel qu’avec les directives données il puisse se reproduire à l’infini, alors la probabilité de le voir apparaître tendra vers 1 à mesure que le nombre de tours tendra vers l’infini.
Or, pendant la phase « chaotique », comme je l’ai évoqué plus haut, le système semble se comporter comme un générateur aléatoire de variété. Donc, le motif devrait apparaître. Il ne resterait qu’à respecter deux conditions. Premièrement, un fois construit, que l’automate puisse l’amorcer, ce qui signifie qu’il doit l’aborder par la bonne case, avec la bonne orientation (là encore, ce n’est qu’une question de nombre d’essais et donc de temps). Deuxièmement, que le motif soit situé aux abords d’un champ vierge de toute interférence.
Ce point relatif aux interférences m’amène justement à penser que si nous nous amusions à encercler la zone utilisée pendant la phase « chaotique » avec des cases noires, l’intersection de « l’autoroute » et des points de ce cercle provoquerait la fin de « l’autoroute » et un retour à la phase « chaotique ». Mais « l’autoroute » finirait inéluctablement par réapparaître dès lors que les conditions citées plus haut seraient réunies.
Bonjour,
Une piste de réflexion: Si on supprime l’aspect chaîne de Makrov du jeu de la fourmi en introduisant une vraie dimension aléatoire à l’état du plateau, on constate que l’autoroute n’apparait plus !
On peut faire cela en rajoutant une ligne au code pour donner l’aspect chat de shroedinger à la couleur de la case (i.e. donner une probabilité de 50/50 non connue tant que la fourmi n’avance pas sur la prochaine case que la case soit blanche ou noire).
(Ceci ne change pas les règles, les cases visitées ne sont plus soumises à cette probabilité si la fourmie doit repasser dessus.)
On montre alors que l’état de départ du plateau conditionne l’apparition de l’autoroute.
Ou encore, que pour toute situtation qui converge vers un schéma donné en tangeante, il existe un état initiale du plateau ou le schéma ne converge jamais.
Bien à vous,
-DAB
Cf fichier :
https://www.dropbox.com/s/gsb8v8yieoiw13g/Copie%20de%20Fourmie%20de%20Langton_GBI2.xlsm?dl=0
ATTENTION NE CLIQUEZ PAS CE LIEN
j’ai cliqué et dès que ça s’est ouvert mon pc a ralenti de plus en plus jusqu’à crasher complètement, obligée de le redémarrer, je sais pas si c’est un virus ou juste un fichier qui demande beaucoup trop de ressources pour s’ouvrir mais dans tous les cas c’est mauvais pour le pc.
Le fichier Excel contient beaucoup de cellules coloriées c’est consommateur de RAM à l’ouverture en effet. Je vais coller le code séparément.
Vous écrivez « Une piste de réflexion: Si on supprime l’aspect chaîne de Makrov du jeu de la fourmi en introduisant une vraie dimension aléatoire à l’état du plateau, on constate que l’autoroute n’apparait plus ! »
Cela coule de source !
L’autoroute, n’est que le résultat de l’ordre premier, directeur, donnée à l’automate. Soit, tourner en rond ou plutôt en carré. Le fait d’avoir introduit un changement de direction, ne change pas l’ordre premier auquel obéit l’automate, mais introduit simplement une itération, c’est à dire, oblige l’automate à définir les couleurs des cases du plateau permettant de répondre à son ordre premier, soit, tourner en carré. Mais cela implique que ce soit le mouvement de la fourmi qui code elle même le plateau sur laquelle elle va pouvoir obéir à l’ordre premier, directeur de tourner en carré, de manière récurrente. Si on ajoute une couleur extérieure, placé sur le chemin de la fourmi, cette couleur détruit le mouvement itératif de la fourmi pour trouver la récurrence définit par l’ordre premier directeur. Cela dit, si vous arrêtez l’interférence, il se peut que la fourmi arrive à retrouver son autoroute, mais pas forcément.
Tout système, quel qu’il soit, est définir par un ordre premier directeur, qui définit la finalité ou but du système, les ordres secondaires ayant alors pour fonction de définir les modes d’exécutions pour atteindre le but (mais aussi pour s’y opposer). Toutefois, la fourmi de Langton est un cas un peu particulier, dans le sens où il n’y a pas d’ordre secondaire, sinon une condition particulière pour introduire l’itération dans le système, car sans ce changement de direction, la fourmi tournerait sur les 4 cases du plateau où elle se trouve, ce qui n’aurait aucun intérêt, mais le changement de couleur ne change pas ce mouvement, elle complexifie seulement cette récurrence du mouvement et dans certains cas, le rend impossible.
La preuve simple, est qu’il n’y a d’aléatoire au mouvement que la première fois, ensuite, les mêmes conditions produiront toujours le même chemin. La notion de chaos ou d’aléatoire est donc trompeuse, fausse, simplement, faire le calcul du chemin, demande infiniment plus de ressources que de parcourir le chemin lui même, parce qu’on doit d’abord passer par une itération et non seulement une récurrence. Or, les calculs mathématiques ne sont capables de définir que des récurrences, pas des itérations. Hors récurrence, les mathématiques ne peuvent définir que des statistiques, probabilité, rien de plus. L’incrémentation de l’ensemble des nombres entiers naturels est une itération, mais de forme récursive, tandis que l’ensemble des nombres premier est aussi une itération, mais pas de forme récursive, parce que c’est chaque nombre premier qui ajoute sa propre récurrence pour donner le nombre premier suivant (dû à la fractalisation en passant de l’addition à la division). Ce qui rend tout calcul impossible, sauf dans l’imaginaire, dans l’aberration des calculs abstraits, mais les grand nombres premiers sont de pseudos nombres premiers, où ce n’est que l’impossibilité de les vérifier par factorisation qui leur donne le caractère de nombre premier. Et ce calcul, échappe aussi aux calculateurs quantiques. Cela suffit à expliquer la flèche du temps (causal).
C’est élémentaire et d’une logique causale imparable, mais ce n’est pas celle qui est enseignée…
Ce que vous dites me semble incorrect : « Tout système, quel qu’il soit, est définir par un ordre premier directeur, qui définit la finalité »
Un système peut converger quelque soit ses conditions initiales, un autre toujours diverger et un troisième être imprévisible. Je vous mets au défi de prédire l’issue de tout système itératif (comme vous l’expliquez très bien) en ne connaissant que l’ordre premier !
La poprosition qui était faite : « Le système fourmie de Langdon diverge toujours ! » i.e. à partir d’un certain nombre d’itérations l’autoroute apparait toujours ». Contre-exemple que non, des conditions initiales particulières montrent que la fourmi avec le même ordre premier ne forme jamais d’autouroute.
Ce que vous dites me semble incorrect : « Tout système, quel qu’il soit, est définir par un ordre premier directeur, qui définit la finalité »
Un système peut converger quelque soit ses conditions initiales, un autre toujours diverger et un troisième être imprévisible. Je vous mets au défi de prédire l’issue de tout système itératif (comme vous l’expliquez très bien) en ne connaissant que l’ordre premier !
—————————
relisez bien, j’écris que l’ordre premier définit la finalité, il est de ce fait, récurrent. Par contre, les ordres second ne sont pas récurrents, ils sont itératifs, parce qu’ils consistent à définir le mode d’exécution ou si vous préférez, les moyens pour atteindre la finalité et leur mise en oeuvre. L’exemple de la fourmi de Langton ne contient pas d’ordre second, mais seulement l’ordre premier, la confusion étant dû à la condition de changement de direction, mais ce changement ne fait qu’inverser le sens de rotation, pas l’ordre en lui même. Simplement, selon les conditions initiales, le système pourra ou non atteindre son but, ce que je reconnais en l’écrivant aussi. Mais il ne faut pas confondre d’un coté, ordre premier directeur, qui définit la finalité du système et de l’autre, les conditions initiales, mais aussi, l’évolution de ces conditions (ce que vous faites !), qui ne sont pas l’ordre, mais l’environnement qui permettra ou non au système d’atteindre le but définit par l’ordre premier. A contrario, les ordre secondaires portent sur la détermination des moyens, car ceux-ci ne dépendent pas d’une intention quelconque, mais de la seule logique causale et d’elle seule. Dans certains systèmes complexe, les ordres secondaires portent aussi sur l’opposition à l’ordre premier. Or, en dehors de l’Univers lui même, tout système entre en interaction avec d’autres systèmes, ce qui rend d’autant plus difficile à un système d’atteindre son but, mais tous obéissent à la logique causale quant à leurs interactions.
Autrement dit, vous pouvez toujours connaître l’ordre premier, directeur d’un système, parce que récurrent, mais vous ne pouvez pas pour autant savoir s’il va atteindre son but, cela dépendra des conditions environnementales et de l’évolution de ces dernières. Qui nécessite l’itération pour chercher à atteindre le but, en fonction des conditions environnementales et des relations de logique causale que cela implique. Sans cela, on connaîtrai tout de l’Univers, de sa vie et de la vie des autres sans avoir à le demander. On peut donc connaître des intentions de chacun, si tant est qu’il ne trompe pas les autres ou/et lui même, mais pas de savoir s’il atteindra son but avant qu’il ait justement fait le chemin, c’est à dire, vécu. La seule manière de surseoir à la logique causale, d’atteindre son but en même temps qu’on l’énonce, c’est de rester confiné dans son propre imaginaire, donc, de ne pas entrer en interaction avec un autre système…Ou de prendre le contrôle des autres systèmes !
Prenons en exemple l’incrémentation des nombre entiers naturels. La récurrence, c’est de dire 1 + 1 + 1 + 1 etc. Cette suite est première et fait naître la suite itérative.
L’itération, c’est de dire 1, 2, 3, 4, etc. C’est toujours obéir au même ordre premier, la même récurrence, mais dont on donne un nom propre à chaque nouvelle incrémentation de 1. Cette itération est de forme récurrente, et de se fait, ne pose aucun problème à calculer n’importe quel nombre instantanément. La subtilité qui n’est pas noté car triviale, c’est que, vis à vis de l’addition et soustraction, tout nombre entier est premier. Par contre, lorsqu’on passe à la division et multiplication et qu’on considère seulement les nombres premiers (en division), ce n’est plus vrai, c’est à dire, je ne peux plus connaître la position d’un nombre premier sans l’avoir calculé, factorisé, parce que l’itération n’est plus de forme récursive, mais aléatoire au premier calcul. Car une fois connu, il est parfaitement déterminé. Il ne prend donc une forme récursive, qu’une fois factorisé. Mais je maintien que, chaque nombre premier ajoutant sa propre récurrence au calcul, il est impossible de connaître un grand nombre premier par une quelconque équation de forme récursive, mais uniquement de donner une probabilité de présence. Pour savoir si un grand nombre est premier, il faut le factoriser. Et factoriser un nombre avec 1 million d’exposant est impossible et surtout, n’a aucun sens logique, seulement la conséquence de l’aberration du cogito humain.
L’être n’a de choix que des finalités ou buts, mais pas des moyens, ces derniers sont le fait de la logique causale et des conditions environnementales, c’est à dire, des autres systèmes en présence. Si les moyens existent déjà dans la réalité, le but peut être atteint, sous réserve de dépasser les résistances éventuelles d’autres systèmes. Si les moyens n’existent pas, soit on peut les créer, soit ils relèvent de l’impossible. Dans le premier cas, on est face à une utopie tant qu’on n’a pas créé les moyens, via notre imagination. Dans le second cas, c’est seulement le monde de l’imaginaire. Les grands nombres premiers, relève du seul imaginaire et ce n’est que l’impossibilité de les factoriser qui permet de faire croire en leur découverte.
« Ce qu’il y a de plus perturbant, c’est que même si on part d’une grille dont les cases sont coloriées aléatoirement en blanc ou en noir, l’autoroute finit toujours par apparaître un jour ou l’autre. »
Non, sur une grille en damier ce n’est pas la même l’autoroute qui apparaît mais un « ptit chemin » sur deux cycles.
pour que le phénomène d’autoroute émerge, il faut que certaines conditions initiales soient réunies (une certaine configuration de cases blanches et noires) et qu’un espace vide soit présent dans une certaine direction de l’espace (un espace dégagé dans une direction donnée). dans ces conditions particulières, le phénomène de l’autoroute apparaît. si une case noire est présente sur le chemin de l’autoroute, alors les conditions de répartitions qui permettent le confinement de la fourmi sont cassées, et la fourmi reprend un parcours chaotique.
Pingback: La fourmi de Langton — Science étonnante #21 - Blog NSellier TV
cela n’a rien de surprenant. il existe une situation, une configuration de l’espace (répartition des cases blancs et noirs) qui fait que la fourmi va invariablement tournée en rond = conditions intiales pour l’apparition d’un puit. dans un espace suffisamment grand, quelque soit la répartition initiale des cases blanches et noires, la fourmi va nécessairement rencontrer à un moment cette configuration d’apparition d’un puit, et va tomber dedans. c’est juste une question de probabilités.
un autre jeu intéressant consiste à mettre 2 fourmi sur un damier vierge au départ et de voir le nombre d’itérations nécessaires au parcours de toutes les cases ? on peut aussi se demander quelle est la distance moyenne d’espacement entre les 2 fourmis (sont-elles proches ou plus souvent éloignées par rapport à une distance moyenne), le nombre de fois où une case est parcourue … que se passe t’il si on introduit des points fixes, qui ne changent pas de couleur ? …. on peut ainsi introduire de nouvelles conditions au jeu initial, se poser de nouvelles questions et obtenir des réponses toutes aussi surprenantes que le phénomène de l’autoroute.
Pingback: La fourmi de Langton - Lycée En Forêt, Montargis
Je pense que le phénomène de Langton est analogue au type de dynamique de retour à l’équilibre tel une pendule, une flaque d’eau
Pingback: La fourmi de Langton — Science étonnante #21 | JetBip
1/12=0.0833333…, une partie élégante et symétrique, 0.0, une partie plutôt cahotique, 083, et une autotoute vers l’infini, 3333…. Cette analogie fait-elle du sens? La fourmi de Langton est-elle en train de nous de nous dire que si on mélange de façon disons aléatoire un certains nombre de paramètres, on finira toujours par aboutir à un nombre complexe i.e. une autoroute vers l’infini ?