Contrairement à Jonathan et Jennifer Hart, les héros de la célèbre série télévisée l’Amour du Risque, la plupart des gens n’aiment pas le risque. C’est ce que les économistes appellent l’aversion au risque. Cette idée à la frontière entre économie et psychologie est riche de surprises et de paradoxes que l’on peut mettre en lumière à travers des expériences.
L’aversion au risque.
Pour un économiste, une situation de risque désigne une situation avec un gain possible, mais à l’issue incertaine. Il s’agit par exemple d’un placement dont le rendement n’est pas garanti, ou simplement d’un jeu de hasard.
Supposons que je vous donne 100€, et que je vous propose de choisir entre les deux options suivantes :
A – Vous partez avec vos 100€
B – On tire à pile ou face. Pile : je reprends mes 100€, Face : je vous redonne 120€ de plus (vous repartez avec 220€).
Que choisissez-vous ?
Si on fait l’expérience réelle, la majorité des gens vont choisir l’option A : le gain est certain, donc sans risque. Et pourtant un rapide calcul nous montre que l’option B est statistiquement plus avantageuse : dans 50% des cas vous repartez les mains vides mais dans les autres 50% vous repartez avec 220€. Soit en moyenne 110€, ce qui est plus élevé que pour l’option A.
Oui mais pour la majorité d’entre nous, ce gain en moyenne plus élevé ne suffit pas à compenser l’incertitude liée au tirage au sort. C’est cette préférence que l’on appelle l’aversion au risque.
L’aversion au risque est-elle rationnelle ?
A un niveau élémentaire de l’analyse économique, l’aversion au risque peut paraître irrationnelle. D’après la théorie économique, un être humain cherche en permanence à maximiser ses gains, et un gain de 110€ est censé être préférable à un gain de 100€.
Un des moyens d’expliquer rationnellement l’aversion au risque, c’est d’introduire un effet dont j’ai déjà parlé ici, et qui dit essentiellement que 100€ ont plus de valeur à nos yeux si on est pauvre que si on est riche. Pour quantifier cette notion de « valeur à nos yeux », les économistes parlent de l’utilité de l’argent. On peut voir l’utilité comme une sorte de plaisir que nous procure l’argent.
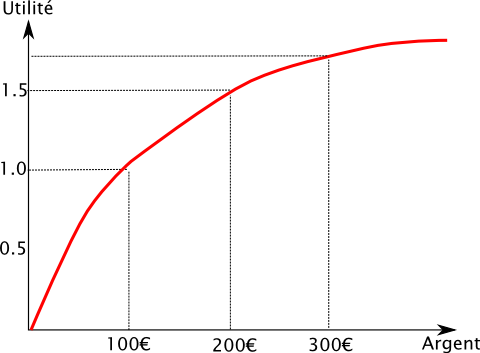
Supposons arbitrairement que 100€ me procurent un plaisir de 1. Alors il est vraisemblable que 200€ ne me procureront pas un plaisir de 2, mais quelque chose d’un peu inférieur, par exemple 1,5.
On peut traduire cet effet par une courbe qui nous donne l’utilité (le plaisir) en fonction de la somme d’argent que l’on possède. La courbe a en général une forme du genre de celle ci-contre.
C’est une courbe qui est de moins en moins pentue. Mathématiquement, on dit que l’utilité est une fonction concave. La concavité de la courbe est la traduction de cette propriété qui dit que plus on est riche, plus le gain de plaisir pour 100€ supplémentaires est faible.
Avec la prise en compte de l’utilité de l’argent, on peut résoudre le paradoxe apparent de l’aversion au risque :
Dans la situation notée A, on gagne 100€ de manière certaine donc notre utilité sera de 1.
Dans la situation B, on gagne à 50% de chance 220€, dont l’utilité est environ 1.6, et à 50% on ne gagne rien (utilité 0). Donc en moyenne le plaisir apporté par la situation B est de 0.8.
Bien que le gain moyen soit plus élevé dans la situation B, l’utilité moyenne est plus faible et il est donc rationnel de préférer la situation A.
Fonctions d’utilité convexes et stratégies footballistiques
En réalité, nous ne sommes pas tous toujours averses au risque. En effet dans certaines situations la fonction d’utilité n’est pas concave et nous incite à prendre des risques. Un exemple ? Le comptage des points dans un championnat de foot, dont j’ai déjà parlé dans mon billet sur la théorie des jeux.
Imaginons que vers la toute fin d’une partie de foot, vous soyez à match nul (vous marqueriez donc 1 point au championnat), mais que vous ayez la possibilité de lancer une dernière attaque très risquée : à 50% de chances vous marquez et vous remportez le match, mais à 50% de chances vous vous prenez un contre et vous perdez le match.
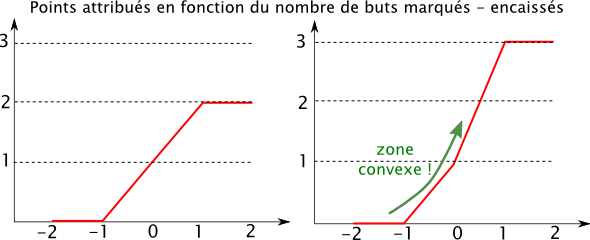
Dans l’ancien système de comptage des points au championnat, la victoire vous rapporte 2 points, alors que dans le système en vigueur depuis 1995, elle vous rapporte 3 points. La figure ci-dessous montre les gains au championnat en fonction du score du match dans les deux systèmes de comptage.
On voit très bien que dans l’ancien système, à match nul on n’a pas intérêt à attaquer car on a autant à perdre qu’à gagner. Mais dans le nouveau système c’est différent : la fonction n’est plus concave puisqu’entre le match nul et la victoire, la pente est plus forte qu’entre la défaite et le match nul. Conséquence : avec la victoire à 3 points on a plus à gagner qu’à perdre : il vaut mieux prendre des risques pour passer de 1 à 3 points, même si ça peut nous coûter de retomber à 0.
On démontre donc bien que le nouveau système de comptage est censé favoriser la prise de risques et donc le jeu offensif et spectaculaire (même si l’analyse empirique semble démontrer le contraire)
En revanche à 1-0, la fonction est à nouveau concave : l’utilité associée à un but supplémentaire est nulle alors que la perte possible si on se prend un but est de 2 points. D’où la stratégie transalpine bien connue du catenaccio. Mais bon là je ne fais que redémontrer la sagesse populaire footballistique…
Quelques paradoxes associés à l’évaluation des risques
Quand il est question de décision en environnement incertain (donc risqué), plusieurs paradoxes ont été relevés par les économistes à partir de situations d’économie expérimentale. L’un des plus connus est le paradoxe d’Allais, mentionné en 1953 par l’économiste (et prix « Nobel » d’économie) français Maurice Allais.
En voici un exemple. Je vous donne le choix entre 2 situations :
A : gagner 100€ de manière certaine ;
B : gagner 150€ avec 90% de chance ;
Les expériences montrent que la majorité des gens vont choisir l’option A, avec un gain certain. Maintenant je vous propose de choisir entre :
C : gagner 100€ avec 10% de chance ;
D : gagner 150€ avec 9% de chance ;
Il se trouve que dans la majorité des cas, nous choisissons plutôt l’option D, car le gain est plus élevé et la différence de probabilité nous paraît négligeable.
Et pourtant les options C et D proposent respectivement des conditions quasi-identiques aux options A et B. En effet l’option C correspond à 90% de chance de ne rien gagner et 10% de jouer à A, alors que l’option D correspond à 90% de chance de ne rien gagner et 10% de jouer à B. Donc rationnellement, si on préfère A à B, on doit préférer C à D.
Le paradoxe d’Allais montre que quand le risque est extrême (faibles probabilités de gagner), notre perception se modifie et nous fait nous éloigner du comportement rationnel.
Ce paradoxe n’est pas le seul des effets intéressants que l’on observe dans les situations réelles ou simulées par l’économie expérimentale, je vous en exposerai bientôt d’autres, mais dans un prochain billet !
13 Comments
Très intéressant billet, qui montre à quel point la perception et la psychologie sont importantes dans les jeux de hasard.
D’ailleurs les opérateurs de loterie analysent cela avec soin pour correctement répartir les gains et la redistribution en fonction des différentes probabilités.
Dans le même genre il y a le paradoxe de l’aversion aux pertes qui n’est pas le symétrique de l’intérêt au gain (autrement dit, on est plus malheureux de perdre un billet de 20€ tombé de sa poche qu’on est heureux d’en trouver un par hasard par terre). J’en ai fait une série de 3 billets (un peu de pub!) ici, là et là.
Tu as raison de faire de la pub 🙂 Je ne connaissais pas tes billets (je ne te lis pas depuis si longtemps !) mais je constate que nous avons les mêmes lectures. Ce qui d’ailleurs me fait avoir des doutes quant à l’existence de ma liberté individuelle et de mon libre arbitre !
Supposons que je vous donne 100€, et que je vous propose de choisir entre les deux options suivantes :
A – Vous partez avec vos 100€
B – On tire à pile ou face. Pile : je reprends mes 100€, Face : je vous redonne 120€ de plus (vous repartez avec 220€).
Je ne voie pas en quoi la deuxième option est plus avantageuse, à moins de refaire le test plusieurs fois sur la même personne…?
Bonne remarque. Il ne s’agit pas là d’un résultat exact mais d’un postulat qui parut raisonnable à un certain moment de l’histoire de la pensée économique. Voici le raisonnement
– en situation certaine (pas de hasard), les individus cherchent à maximiser leurs gains
– en situation probabiliste où l’on répète plein de fois l’expérience, maximiser ses gains revient à maximiser l’espérance, c’est à dire la moyenne probabilisée sur toutes les situations.
Donc une hypothèse raisonnable pour essayer de modéliser le comportement de l’être humain devant prendre une décision en situation probabiliste, c’est de supposer qu’il va chercher à maximiser l’espérance de ses gains.
Bien sûr on aurait pu prendre d’autres hypothèses, par exemple : « l’être humain cherche à maximiser le minimum de ses gains ». Mais c’est peu réaliste car entre 10000€ à 99% de probabilité et 10€ certains, les gens choisissent en général la première situation et pas la seconde.
Bref « maximiser l’espérance de ses gains » paraissait l’hypothèse la plus simple à même de coller au comportement des humains…jusqu’à ce qu’on introduise le concept d’utilité !
Pingback: Le singe, un homo économicus irrationnel comme les autres « Science étonnante
Bonjour,
Excellent article à la fois accessible au grand public et intellectuellement exigeant.
Il me semble qu’il y ai une petite erreur d’analyse. Contrairement à ce qu’affirme Brigitte Nussbaum (dont vous donnez le lien après « même si l’analyse empirique semble démontrer le contraire ») le nouveau système de comptage de point en football n’a pas été introduit par la FIFA pour « favoriser la prise de risques » mais plus précisément pour éviter les collusion entre équipe afin de se partager les deux points d’un match nul. Ce choix a été pris à cause du le « match de la honte » (coupe du monde de football 1982) qui avait vu l’Allemagne et l’Autriche s’entendre au dépend de l’Algérie.
Pingback: Méfiez-vous d’un juge affamé ! | Science étonnante
Bonjour !
La gestion du risque c’est tout le problème des joueurs et des traders. Au poker on essaie de favoriser les probabilités de gains. En bourse aussi. Pour cela on utilise ce que l’on appelle l’analyse technique : des indicateurs mathématiques simples qui font basculer les dés du bon côté (la plupart du temps). On essaie aussi de choisir les meilleurs cartes (euh, actions), car, contrairement au poker, on peut choisir les cartes.
Bonjour,
Il me semble que le paradoxe d’Allais ne tient pas : les 2 choix (A ou B, et C ou D) sont incomparables, et la conclusion « rationnellement, si on préfère A à B, on doit préférer C à D » est fausse.
Je m’explique :
Le choix 1 (A ou B) n’est pas, par nature, un jeu ; alors que le choix 2 (C ou D) est par nature un jeu (ou alors si l’on tient vraiment à dire que le choix 1 est un jeu, nous dirons que sa nature diffère complètement de celle du jeu du choix 2). La psychologie de la personne à qui on soumet les choix est affectée par cette différence de nature, ce qui rend les expériences incomparables.
Je développe :
Le choix 1 peut se traduire par : soit je te donne 100 euros, soit on joue à un jeu de hasard dans lequel tu peux gagner 150 euros ou rien.
Le choix 2 peut se traduire par : nous allons jouer à un jeu de hasard, tu peux gagner 100 euros, ou 150 euros, ou rien.
Au choix 1 on n’est pas considéré a priori comme un « joueur », on a la possibilité de jouer à un jeu, mais on n’est pas obligé, et dans la majorité des cas on ne le fait pas, c’est rationnel car il y a un risque de perdre les 100 euros qui nous sont généreusement donnés.
Au choix 2, on est considéré a priori comme un joueur, on est invité à jouer à un jeu gratuitement, on n’a « rien à perdre », et il est rationnel en tant que « joueur qui n’a rien à perdre » de choisir de maximiser ses gains et de prendre le risque maximal tant ce risque est proche du risque minimal.
J’affirme ainsi que choisir A puis choisir D est rationnel, et que les 2 expériences sont incomparables.
Qu’en pensez-vous ?
Pingback: Connaître le sexe de son bébé influence-t'il le comportement des parents ? | Bienheureusement ! - Bien-être, Santé & Developpement Personnel
Pingback: 5 freins à l'innovation et comment les éviter - NovoLaB
Pingback: Faut-il commander la glace vanille ? - Idées transverses