Le dilemme du prisonnier

« Alors voilà, Clyde a une petite amie… »

Bonnie et Clyde viennent de se faire coffrer par la police. Bon il faut dire qu’il y a moins d’une semaine ils ont réussi un braquage retentissant. Certes ils ont été arrêtés, mais malgré tous les efforts des enquêteurs, les indices sont bien maigres pour les inculper de ce crime, et la police espère bien les faire avouer.

Cependant comme les enquêteurs savent qu’ils ne lâcheront jamais le morceau directement, ils décident de les interroger séparément, sans qu’ils puissent se parler. A chacun d’eux on offre le choix suivant : soit se taire, soit balancer son complice.

Les conséquences possibles pour eux sont les suivantes :

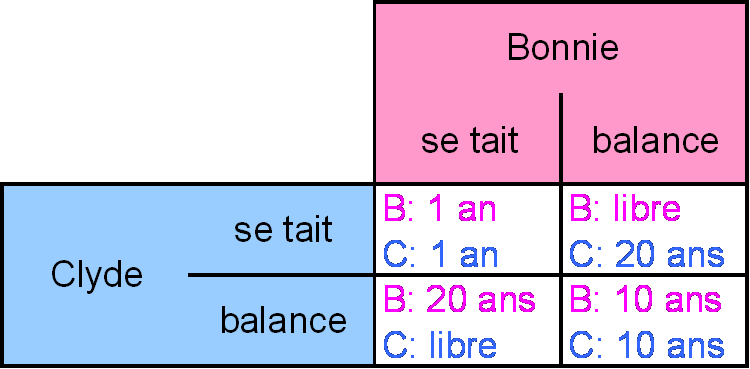
• si Bonnie et Clyde se balancent mutuellement, ils prennent chacun 10 ans de prison.
• si l’un balance son complice alors que l’autre se tait, le traitre ressort libre alors que l’autre malheureux fait 20 ans de prison.
• s’ils se taisent tous les deux, on ne peut pas les inculper pour le braquage alors on les inculpe pour un délit mineur et ils font chacun seulement 1 an.

Ceci est résumé dans le tableau suivant :

Voici ce que se dit Bonnie : « Si Clyde me balance, j’ai intérêt à le balancer aussi, pour faire seulement 10 ans au lieu de 20. Et si Clyde se tait, j’ai quand même intérêt à le balancer pour sortir libre immédiatement. Donc quel que soit le choix de Clyde, mon intérêt est de le balancer ! ».

Bien entendu Clyde, qui n’est pas plus bête que Bonnie, tient exactement le même raisonnement, et il conclut que quelque soit le choix de Bonnie, il a intérêt à la balancer. Et le résultat est sans surprise : Bonnie et Clyde se balancent mutuellement. Evidemment on comprend vite qu’ils n’ont pas dû prendre la bonne décision, puisqu’ils vont faire 10 ans chacun, alors que s’ils s’étaient entendus, ils n’auraient fait qu’un an. Et pourtant chacun n’a fait qu’optimiser sa propre situation.

Cette situation est ce qu’on appelle le dilemme du prisonnier : si chacun raisonne de manière égoïste (et non-collaborative), on aboutit à une situation plus mauvaise pour tout le monde que si on cherche à s’entendre (la solution collaborative). Le dilemme du prisonnier s’applique à bien d’autre cas que Bonnie et Clyde.

Ami ou Ennemi ?

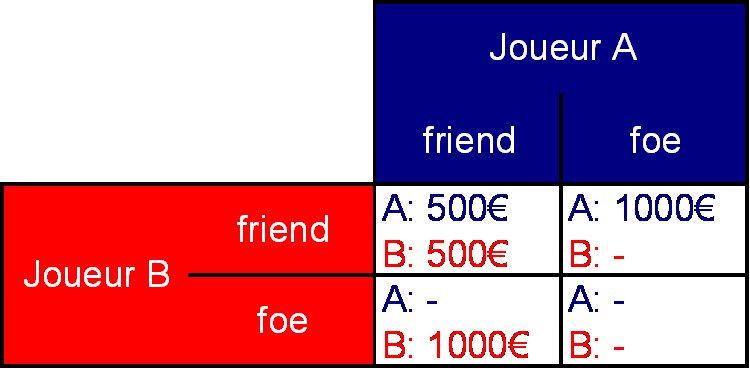
Une autre illustration classique est donnée par le jeu « Friend or Foe » (Ami ou Ennemi) diffusé à la télé américaine entre 2002 et 2004. Dans ce jeu, deux joueurs qui ne se connaissent pas jouent ensemble pour gagner de l’argent, par exemple 1000 €. Puis à la fin de la partie on décide de la répartition du gain commun. Pour cela chacun des deux joueurs choisit en secret soit Friend, soit Foe. Si les deux choisissent Friend, ils se partagenet équitablement le magot (500€ chacun). Si les deux choisissent Foe, ils repartent tous les deux les mains vides, mais si l’un choisit Foe et l’autre Friend, Foe prend tout le magot et Friend repart sans rien. Comme dans le cas du dilemme du prisonnier on peut résumer cette situation avec un petit tableau :

Là aussi la solution collaborative est préférable à la solution non-collaborative, qui est pourtant plus tentante si on raisonne égoïstement.

Les jeux à somme non-nulle

Dans la plupart des jeux auxquels on joue pour s’amuser (par exemple le poker), ce que l’un des joueurs gagne, l’autre le perd forcément, et réciproquement : c’est ce qu’on appelle un jeu à somme nulle. Dans les jeux à somme nulle, on n’a aucun intérêt à collaborer, et les situations comme celle du dilemme du prisonnier ne se produisent pas. Les jeux à somme constante sont exactement comme les jeux à somme nulle : si la somme à répartir ne dépend pas du choix des joueurs, il n’y a pas non plus de solution collaborative à trouver.

Par contre, vous voyez bien que Friend or Foe est un jeu à somme non-constante : suivant les choix des joueurs, le total de ce que la banque va leur distribuer peut varier de 0 à 1000€. Dans les jeux à somme non-constante, il peut exister des solutions collaboratives plus intéressantes que les solutions non-collaboratives.

Les jeux à somme non-constante sont omniprésents dans la vie de tous les jours, en voici 3 exemples classiques du plus réjouissant au plus grave : le football, les prix en oligopole et la guerre nucléaire.

Le football : match aller / match retour

Jusqu’à il y a quelques années en football, une victoire rapportait 2 points, et un match nul 1 point. Il s’agissait bien d’un jeu à somme constante puisqu’à chaque match, quel que soit le résultat, la Ligue distribuait 2 points. On n’avait donc aucun intérêt à s’entendre.

Depuis que la victoire est récompensée de 3 points, le jeu n’est plus à somme constante puisque suivant le cas ce sont 2 ou 3 points qui seront distribués. Il peut donc exister des solutions collaboratives qui profitent à tout le monde. Par exemple si deux équipes de niveau équivalent s’affrontent lors d’un match aller et d’un match retour, ils risquent de s’en sortir avec deux matchs nuls et seulement 2 points chacun, ce qui est la solution non-collaborative. Par contre s’ils sont malins, ils choisissent la solution collaborative en se laissant gagner chacun un match, et en empochant tous les deux 3 points.

Le cas du football montre bien comment le passage à un jeu à somme non-constante rend les ententes collaboratives possibles !

Les prix en oligopole

Un oligopole est un marché économique pour lequel il n’existe que peu de fournisseurs. Prenons l’exemple des abonnements de téléphones portables et imaginons que seuls SFR et Bouygues soient fournisseurs. Chacun d’eux peut décider soit de baisser les prix, soit de maintenir les prix. Si les deux maintiennent des prix élevés ils empochent chacun 3 milliards. Si un seul baisse les prix, il raffle tous les clients de l’autre et empoche le pactole (5 milliards). Enfin si les deux baissent leurs prix, ils se livrent à une guerre des prix dommageable pour les deux, et gagnent chacun seulement 1 milliard.

Pour les fournisseurs, la solution collaborative (entente pour maintenir les prix élevés) est préférable à la solution non-collaborative (guerre des prix). Bien sûr pour le consommateur, c’est l’inverse ! C’est pourquoi l’entente sur les prix est sévèrement punie par les lois chargée de préserver la concurrence ! Mon exemple du téléphone portable n’est d’ailleurs pas innocent.

La guerre nucléaire

Washington et Moscou sont en pleine guerre froide. Ils ont chacun le choix entre consacrer leur argent soit à l’armement nucléaire, soit à l’éducation et la santé dans leur pays. Si l’un seulement acquiert des armes nucléaires, il détruit l’autre. Si les deux s’arment la guerre froide continue, et si les deux poursuivent des programmes éducatifs et de santé, tout le monde s’en retrouve plus heureux. A nouveau la solution collaborative (santé et éducation dans les deux pays) est la meilleure, mais la solution non-collaborative (guerre froide) est celle qui s’impose sans concertation.

Comme on peut le voir, les implications du dilemme du prisonnier sont partout ! Pas étonnant que ce sujet soit devenu une branche à part entière de l’économie, de la psychologie comportementale et des mathématiques, sous le terme  un peu plus générique de « Théorie des jeux ». Nous aurons j’espère l’occasion d’en reparler…

Crédits

Bonnie & Clyde, Wikimedia Commons